基于改进的METRIC模型的农田潜热通量估算
余 健, 姚云军, 赵少华, 贾 坤, 张晓通, 赵 祥, 孙 亮
(1.北京师范大学遥感科学国家重点实验室,遥感科学与工程研究院,北京 100875; 2.环境保护部卫星环境应用中心,北京 100094; 3.美国农业部水文与遥感实验室,贝茨维尔 MD20705)
0 引言
潜热通量是指地表发生土壤水分蒸发、水体或植被截留蒸发和植物体内水分的蒸腾过程中下垫面与大气水分热交换能量的总称,在农业作物估产、大面积干旱监测和水资源管理中具有重要作用。我国是干旱发生频率较多和水资源匮乏的国家,特别是华北平原地区,多年来农业粮食作物因缺水减产的情况较为严重。为合理地管理农业水资源和防旱抗旱,有必要开展农田潜热通量的估算研究。
遥感高度融合了地表空间异质信息,能够实现区域和田块尺度上的潜热通量估算和水分监测[1-2]。在众多的遥感潜热通量估算方法中,基于热红外遥感信息潜热通量估算算法受到研究者的广泛关注。1973年,Brown等[3]根据能量平衡原理和作物阻抗原理建立了作物阻抗—蒸散发模型,成为热红外遥感温度应用于作物潜热通量模型的理论基础; 1983年,Seguin等[4]利用热红外遥感数据反演地表温度估算日蒸发量,并作了进一步的阐释,该方法在大尺度潜热通量遥感估算中被广泛应用; 随后,Shuttleworth等[5]提出了经典的双层模型,后于1991年进行了修正[6],融合了植被和土壤的蒸散作用; Bastiaanssen等[7-8]开发出地表能量平衡算法(surface energy balance algorithm for land,SEBAL)模型,结合Landsat TM遥感影像反演了土耳其的盖笛兹灌溉盆地的显热和潜热通量,该模型在继后的150多个研究项目中得到了应用。
最近,基于高空间分辨率的农田潜热通量模型受到了许多学者的青睐。Allen等[9-10]于2007年提出了基于高分辨率和内在校准的蒸散估算法(mapping evapotranspiration at high resolution and with internalized calibration, METRIC)估算月度和季节性蒸散与潜热通量,并将其应用于美国爱达荷州所需地下水开发量的计算和水权调度及计划; 国内何磊等[11]和连晋姣等[12]利用METRIC和地表能量平衡系统(surface energy balance system, SEBS)模型估算了黑河流域的蒸散,验证结果表明SEBS-METRIC方法可以用来估算黑河流域中游作物农田蒸散量,得出了在作物生长季内黑河流域中游地区蒸散量空间分布差异较大,大致在398~709 mm之间变化的结论。尽管METRIC模型物理意义明确,应用广泛,但在具体区域潜热通量反演实践中受限制于地表观测数据和气象数据的缺失,往往导致反演精度不够。
本文在分析以上方法与模型优缺点的基础上,利用Landsat热红外数据获取的地表温度以及可见光和近红外波段获得的归一化植被指数(normalized difference vegetation index,NDVI)改进地表粗糙度,提出基于地表粗糙度改进的METRIC模型来估算农田潜热通量,并利用海河流域怀来和密云2个农田通量观测站的通量观测数据验证精度,为开展大范围的农田水分监测和农业灌溉提供一种简易可行的方法。
1 材料与方法
1.1 研究区概况及数据源
本文的研究区海河流域位于E112°~120°,N35°~43°之间,流域面积约为32万km2(图1)。
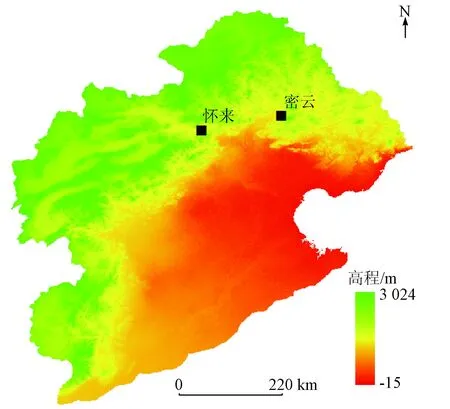
图1 研究区通量观测站点空间分布图Fig.1 Location of 2 flux tower sites throughout the study area
研究区地势为西北高东南低,大致分高原、山地及平原3种地貌类型,西部为黄土高原和太行山区,北部为蒙古高原和燕山山区。研究区属于半湿润半干旱地区,年平均降水量为540 mm,年陆表蒸散量为470 mm[13-14]。土地覆盖类型有旱地、草地、林地、灌木林、水田、湿地、水体、滩地和裸地等。本文先选取怀来和密云站做站点验证分析,再以怀来站为中心,选取约24 km×24 km的样带区域进行空间分析,样带区域包含海河流域主要的土地覆盖类型,能较好地代表海河流域的耗水特征。另外在样带尺度进行分析可以避免遇到云覆盖影像的概率,从而提高影像的时间分辨率。
遥感数据采用Landsat5和Landsat8的原始影像和地表反射率数据,其中Landsat5热红外波段空间分辨率为120 m,Landsat8热红外波段空间分辨率为100 m,其余波段空间分辨率为30 m,数据来自美国地质调查局数据中心(http: //earthexplorer.usgs.gov/)。研究时间段共获取影像58景,其中怀来站研究时间为2013—2014年,获取28景影像; 密云站研究时间为2008—2010年,选取30景影像。因为云或云影对地表温度的反演结果有很大影响,只选取了晴空条件下的影像进行遥感估算。
气象和涡度相关观测数据由寒区旱区科学数据中心提供(http: //westdc.westgis.ac.cn/),其中气象数据主要包括气温、相对湿度、风速、太阳辐射和地表温度等。
本研究中在计算相关地表参数时需要对影像进行预处理,包括辐射定标、几何纠正和图像裁剪等。另外需注意的是要将影像的热红外波段重采样成30 m×30 m,与可见光和近红外波段保持一致。
1.2 地表参数计算
1.2.1 地表温度反演
在经典METRIC模型中,对地表温度的计算是采用热红外辐亮度通过对比辐射率的校正所得,而本文采用覃志豪的单窗算法[15-16]计算得到,即
Ts={a(1-C-D)+[(b-1)(1-C-D)+1]Tb-DTa}/C,
(1)
式中:Ts为地表温度,K; a,b为常量;Tb为亮度温度,K;Ta为大气平均作用温度,K;C和D为中间变量,由大气透射率和地表辐射率计算可得。
1.2.2 地表净辐射估算
瞬时地表净辐射Rn是指地表吸收的太阳总辐射和地表有效辐射之差,其表达式为
Rn=(1-α)RS↓+RL↓-RL↑-(1-ε)RL↓,
(2)
式中:α为地表反照率;RS↓为下行短波辐射,W/m2;RL↓为下行长波辐射,W/m2;RL↑为上行长波辐射,W/m2;ε为地表比辐射率。各辐射通量的计算方法为
(3)
(4)
(5)
式中: Gsc为太阳常数(本文取1 367 W/m2);θrel为太阳入射角,rad;τsw为大气透射率;d为相对日地距离;εa为大气发射率; σ为Stefan-Boltzmann常数,本文取5.67×10-8W/(m2K4);Td为近地表空气温度,K。由于大气长波辐射是来自整个大气层,区域内差异较小,而近地表空气温度不好获取,因此取水分含量较高的地表温度代替近地表空气温度,或取冷点的地表温度作替代。
1.3 METRIC模型
1.3.1 METRIC模型框架
传统的METRIC模型[9]是基于能量余项法计算潜热通量,即
LE=Rn-G-H,
(6)
式中:LE为瞬时潜热通量,W/m2;G为瞬时土壤热通量,W/m2;H为瞬时显热通量,W/m2。其中H和G分别为
(7)
G=(Ts-273.15)(0.003 8+0.007 4α)(1-0.98NDVI4)Rn,
(8)
式中:NDVI为归一化植被指数;ρα为空气密度,kg/m3;Cp为空气定压比热,J/(kgK); dT为地气温差,通常指z1和z2高度之间的温差(一般取z1=0.01 m,为地表高度,z2=2 m,为常规气象站高度);rah为热量传输空气动力学阻抗,s/m。
METRIC模型假设dT与Ts成正比,即
dT=cTs+d,
(9)
式中c和d为经验系数,由遥感图像上的极端点(冷热点)的相关参数计算得到。
在METRIC模型中,假设研究区土壤水分存在2种情况: ①极端干燥环境下,没有水分的蒸发,潜热通量基本为0,而显热通量达到最大,即热点,本文取温度较高(图像最高温度的0.95倍)且没有植被覆盖(NDVI<0.3)的像元; ②湿润环境下,此时水分蒸发达到最大,而显热通量达到最小值,即冷点,本文取温度较低(一般约取1.05倍的图像中的最低温度)且植被茂密(NDVI>0.7)的像元。
故热点的显热通量和冷点的潜热通量分别为
Hhot=Rn,hot-Ghot,
(10)
LEcold=Rn,cold-Gcold-Hcold,
(11)
式中:Hhot和Hcold分别为热点和冷点的显热通量,W/m2;Rn,hot和Rn,cold分别为热点和冷点的瞬时净辐射通量,W/m2;Ghot和Gcold分别为热点和冷点的土壤热通量,W/m2;LEcold为冷点的潜热通量,W/m2。
METRIC算法通过迭代计算热像元rah,结合冷像元信息求解影像内系数c和d。初始假设大气中性稳定,rah计算公式为
(12)
式中: k为von Karman常数,本文取0.41;u*为摩擦风速,m/s,在中性大气条件下的计算公式为
(13)
式中:u200为200 m高空处风速,m/s;zom为地表粗糙度。
1.3.2 地表粗糙度参数改进
在对地表粗糙度的估算上,研究学者们发展了许多方案,如利用粗糙度与叶面积指数(leaf area index,LAI)之间的关系来计算地表粗糙度,即
zom=0.018LAI。
(14)
Moran等[17]研究发现,地表粗糙度和光谱反射有很大的相关性。因此,本研究通过建立zom与NDVI的经验关系估算zom。本文采用粗糙度zom与NDVI之间的关系进行粗糙度估算,关系表达式为
zom=exp(a1+b1NDVI)。
(15)
确定回归参数a1和b1包括以下3个步骤: ①在研究区域选取一定数量的样本区域,测量出样本区域的平均株高h,根据公式zom=0.123h算出样本区域的粗糙度[17]; ②在计算得到的NDVI影像上找出对应样本区域的像元,找出像元的NDVI值; ③利用非线性拟合的方法算出回归参数。本文拟合得到的粗糙度和NDVI关系为
zom=exp(-6.57+7.33NDVI)。
(16)
研究区域的zom取值主要集中在0.01~0.03 m之间,均值在0.018 m左右相当于植被株高在15 cm左右,这对于对应测量的时间段样本区下垫面植被类型是玉米来说是合理的。
2 结果与讨论
2.1 地表温度和地表净辐射验证
为了验证Ts反演的精度,将其与站点观测值进行相关分析。从图2(a)可以看出,反演得到的Ts值的平均误差是-1.65 K,均方根误差为3.4 K,相关系数平方为0.93,经统计检验,达到显著水平(p<0.05)。理想状况下遥感地表温度反演误差为1 K之内,然而由于受到观测数据误差、复杂地表、尺度差异等多种因素导致误差在3 K左右,可见单窗法反演地表温度的精度能满足METRIC模型的要求。
基于地表辐射平衡公式计算的净辐射与通量观测数据进行对比,以此检验算法估算的有效性。由图2(b),估算的净辐射值的偏差是8.28 W/m2,均方根误差为32.94 W/m2,相关系数平方为0.95(p<0.05),由此可知遥感估算净辐射通量结果是可以接受的。
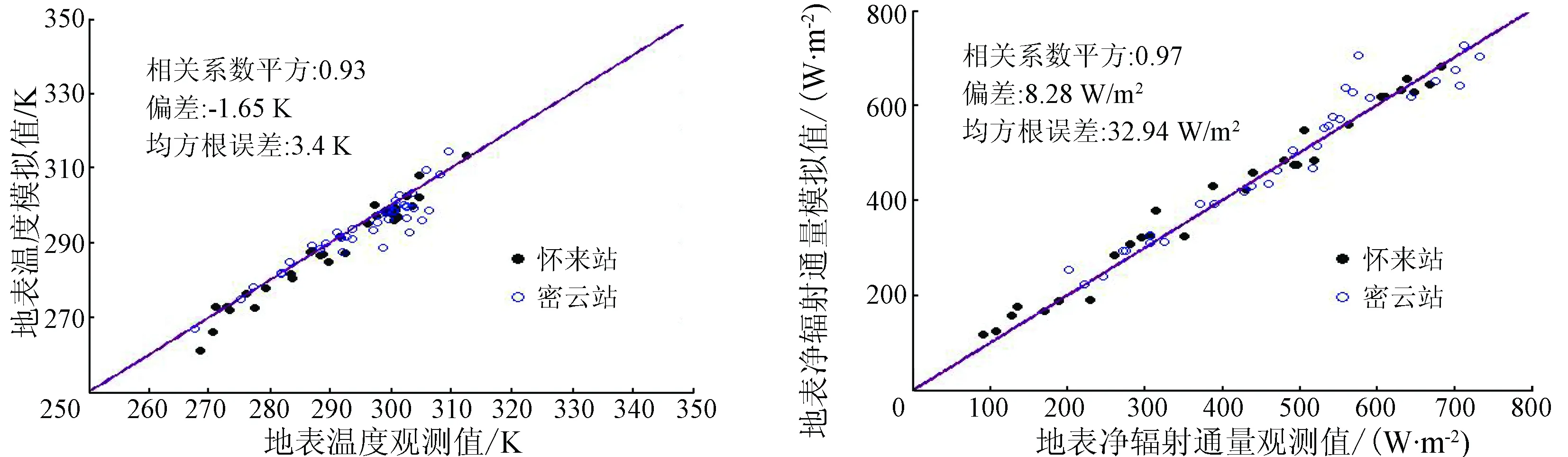
(a) 地表温度(b) 地表净辐射通量
图2地表温度及地表净辐射通量与站点观测值散点图
Fig.2Scatter-plotofretrievedversusobservedTsandestimatedversusobservedRn
2.2 潜热通量验证与算法比较
根据地表粗糙度改进的METRIC模型先估算显热通量H,进而推算潜热通量LE,模拟值与观测值的关系如图3所示。
(a) 改进METRIC模型模拟显热通量 (b) 改进METRIC模型模拟潜热通量
(c) 改进METRIC模型模拟地表通量 (d) 传统METRIC模型模拟地表通量
图3模拟值与站点观测值散点图
Fig.3Scatter-plotofestimatedandground-measuredvalues
图3(a)所示,显热通量的相关系数平方为0.89,偏差为1.48 W/m2,模型模拟的结果显著性明显。最后利用能量余项法作差得到潜热通量,如图3(b)所示,模型计算的潜热值相关系数平方为0.97(p<0.05),偏差为2.31 W/m2,均方根误差为31.06 W/m2,进一步表明METRIC模型估算该区域的农田潜热通量具有较高的模拟精度。本文同时也利用怀来站的部分影像进行传统的METRIC模型估算,图3(c)是地表粗糙度改进的METRIC模型模拟的地表通量估算效果,图3(d)是传统METRIC模型模拟的地表通量估算效果。可以看出,传统的METRIC模型模拟的显热通量和潜热通量结果验证散点图中值分散,估算结果与站点观测值的误差在50~100 W/m2左右,而地表粗糙度改进的METRIC模型模拟的结果与观测值的误差基本在50 W/m2以下,并且经过地表粗糙度的改进后,相关系数平方从0.9提高到0.96,偏差和均方根误差都显著减小,这说明地表粗糙度改进的METRIC模型估算结果更为合理准确,同时也更适用于海河流域的潜热通量估算。
2.3 潜热通量制图与分析
选取怀来观测区域2014年第238日遥感影像对瞬时潜热通量进行制图与分析,由于水体潜热通量估算影响因素较多,本研究采取Priestley-Taylor模式对水体潜热通量进行了单独计算。从图4(a)可以看出,潜热通量的差异明显,变化范围大致在30~830 W/m2,均值约为470 W/m2。水体的潜热通量较大约在700~750 W/m2之间,而处于河边的滩地由于土壤含水量较高,潜热通量也较高,主要集中在550 W/m2左右; 农田的潜热通量呈偏峰型,众数在450 W/m2左右,此时处于夏季,玉米地处于生长季; 林地日潜热通量众数在550 W/m2左右,这主要是由于夏季植被覆盖率较高; 而处于农田旁边的居民建设用地潜热通量也较高(约为480 W/m2),是由于居民往往在居住地附近种植瓜果蔬菜; 另外官厅水库边草地的潜热通量主要集中在350 W/m2。图4(b)与图4(a)空间格局相同,但整体模拟值偏低。
由图4(c)对比后发现,地表粗糙度改进的METRIC模型模拟研究区的潜热通量增大,这是由于传统的METRIC模型地表粗糙度存在较大偏差导致潜热通量偏小。同时发现,模型的改进对农田和的影响比较大而对水体的影响比较小,这是因为本文主要是对模型中地表粗糙度和地表温度进行改进以及对坡度坡向进行纠正。此外在第238日这天,站点的观测值为487.7 W/m2,传统METRIC估算值为403.3 W/m2,地表粗糙度改进后的估算值为501.3 W/m2,粗糙度改进后的模型估算值和观测站观测值之间误差更小,说明地表粗糙度改进的METRIC模型模拟更加理想。
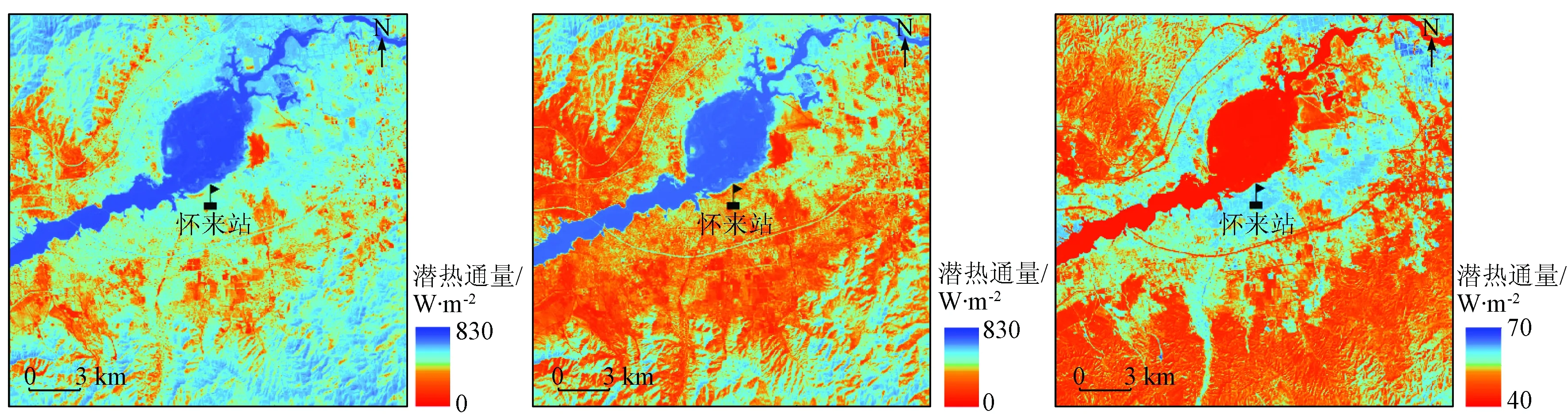
(a) 改进METRIC模型模拟潜热通量空间分布 (b) 传统METRIC模型模拟潜热通量空间分布(c) 本文模型与传统模型模拟潜热通量差值
图4改进METRIC模型与传统模型模拟潜热通量分布及其差值分布
Fig.4SpatialdistributionofLEusingimprovedMETRIC,traditionalMETRICandtheirdifferences
3 结论
利用Landsat热红外数据获取的地表温度以及可见光-近红外数据获得的归一化植被指数(NDVI),改进地表粗糙度,提出基于地表粗糙度改进的METRIC模型来估算农田潜热通量,并利用海河流域怀来和密云2个农田通量观测站的通量观测数据验证该算法的精度,得出的结论如下:
1)基于地表粗糙度改进的METRIC模型与实测潜热通量之间具有较好的相关性,相关系数平方可达0.97,经统计检验,达到显著水平(p<0.05)。
2)尽管基于地表粗糙度改进的METRIC模型和传统的METRIC模型都能模拟农田潜热通量,但是基于地表粗糙度改进的METRIC模型的模拟值与实测潜热通量的相关性更好,表明了改进模型的优越性。
3)从潜热通量空间分布来看,地表粗糙度改进的METRIC模型模拟研究区的潜热通量值比传统METRIC模型模拟精度要高,模拟效果更加可靠。然而,由于数据获取的局限性,本文只采用了海河流域2个站点通量数据进行这些模型的验证与比较,在其他区域的验证与比较仍需要进一步研究。

