基于KL-HVD的转子振动故障诊断方法研究

朱霄珣， 周 沛， 苑一鸣， 徐博超， 韩中合

(华北电力大学 动力工程系，河北 保定 071003)

时频分析[1-2]作为一种现代信号处理方法，能够有效地从非线性、非平稳振动信号中提取故障信息，是故障诊断的关键步骤。目前较为常见的时频分析方法有小波分析、LMD和EEMD等。但是小波基[3]的选择具有主观性，LMD和EEMD都存在模态混叠[4-5]、幅值失真等问题。这些问题都会降低故障诊断的精准度。希尔伯特振动分解(Hilbert Vibration Decomposition，HVD)方法[6]是2006年Feldman在希尔伯特变换基础上提出的一种非平稳信号分析方法。HVD不仅保留了分解的自适应性，而且克服了EEMD和LMD分解过程中对相近频率无法分开的缺陷[7-8]。对于倍频段明显的转子故障信号，HVD更能全面反映其时频的变化特征。

然而，作为一种新方法HVD同样存在不足：虚假分量就是其中较为突出的问题。虚假分量是HVD分解过程中产生的虚假成分，只有对其进行甄别，才能准确分析与提取振动信号特征。

针对该问题，本文提出了基于K-L散度的HVD虚假分量识别方法(KL-HVD)，利用K-L散度[9]定量的刻画各个分量与原信号间的距离，并通过与阈值的比较，识别虚假成分。

另外，文中分别利用互信息及相关分析等手段对虚假分量问题进行研究，并将三种方法应用于实际振动问题分析。通过实验研究发现，相对于互信息及相关分析，K-L散度值能够更加清晰的区分真实成分与虚假分量。证明了KL-HVD方法有效地解决了HVD中的虚假分量问题，对实际问题具有更高的分析精度。

1 希尔伯特振动分解法

1.1 基本原理

HVD方法可以自适应的将一非稳定连续信号分解为多个幅值大小不同的分量之和，具体分解步骤如下[10]：

(1)估计幅值最大分量的瞬时频率。以一两分量非平稳信号x(t)为例：

(1)

假设a1(t)>a2(t)，通过希尔伯特变换求得瞬时频率可表示为：

ω(t)=ω1+

(2)

式(2)表明ω(t)有两部分组成，一部分是幅值最大分量的瞬时频率ω1，另一部分是相对于ω1快速变化的高频振荡部分。因此，实际中可以利用积分和低通滤波器去除ω(t)的高频振荡部分，将ω1估计成幅值最大分量的瞬时频率。一般实际情况下，x(t)含有更多的分量，且瞬时频率表达式更为复杂，但仍可以用低通滤波器方法提取出幅值最大分量的瞬时频率。

(2)同步检测求瞬时幅值。将上述估计的瞬时频率看作参考频率ωr，将信号x(t)分别与两参考正交信号相乘，得下面表达式：

利用低通滤波器滤除式(3)、式(4)后半部分，得：

(5)

(6)

求得瞬时幅值和相位：

(7)

(8)

(3)通过上述步骤提取幅值最大分量x1(t)，并将x(t)与x1(t)的差作为新的初始信号，即：

xN-1=x(t)-x1(t)

(9)

重复以上(1)、(2)两步依次获得不同幅值的分量。将式(9)的归一化标准差作为迭代终止条件σ，当σ<0.001[11]时迭代停止。

1.2 HVD实验应用研究

转子不对中和动静碰摩信号都存在高倍频，在频谱图上较为相似。同时，高倍频分量在分解过程中常常“湮没”于能量较大的工频分量中，不易被分离开。本节以这两种故障为研究对象，基于HVD方法对其进行分析。同时为了进行对比研究，本节同样将EEMD方法应用于故障信号的分析。

利用Bentley转子振动实验台模拟转子不对中和动静碰摩故障，转速为3 000 r/min，采样频率为1 280 Hz。两种故障数据时域图和频谱图见1、图2。

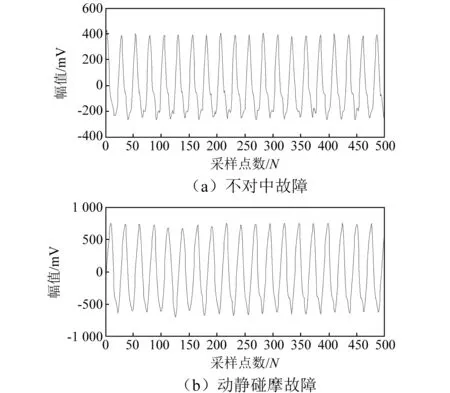
图1 信号时域图Fig.1 signal time domain

图2 信号频谱图Fig.2 signal spectrum

对于两种故障，首先利用EEMD方法进行分析，结果如图3所示。

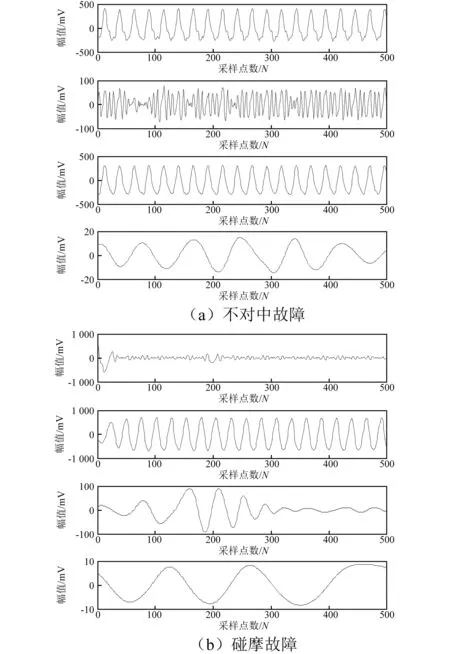
图3 EEMD分析结果Fig.3 EEMD analysis results

从图3可以看出，在处理分量间具有较大能量差异的窄带多分量信号方面，EEMD存在明显不足[12]：高倍频湮没在工频成分中，分解结果存在严重的模态混叠和幅值失真现象。

从图4可以看出，HVD明确地分出了各倍频段分量(分解结果的前4阶)，更能准确的表征故障信号的本质特征，具有更高的分解精度。HVD方法基于严格的数学证明，通过希尔伯特变换和积分滤波有效的滤除了多分量信号中的高频成分，能够分出频率相近的不同单分量。

1.3 虚假分量问题

然而，从图4中还可以发现，信号经HVD分解后会得到若干个分量，这些分量中有一些是多余、无意义的。与频谱图对照并通过人工分析可以识别前4阶分量为真实成分，其余分量是多余的。这些多余的分量被称为“虚假分量”。

虚假分量的存在影响了故障特征信息的准确提取，制约了HVD方法的实际应用。虚假分量有时可以通过人为判断，但显然这是一种粗略的估计，需要定量的方法来识别和去除虚假分量。

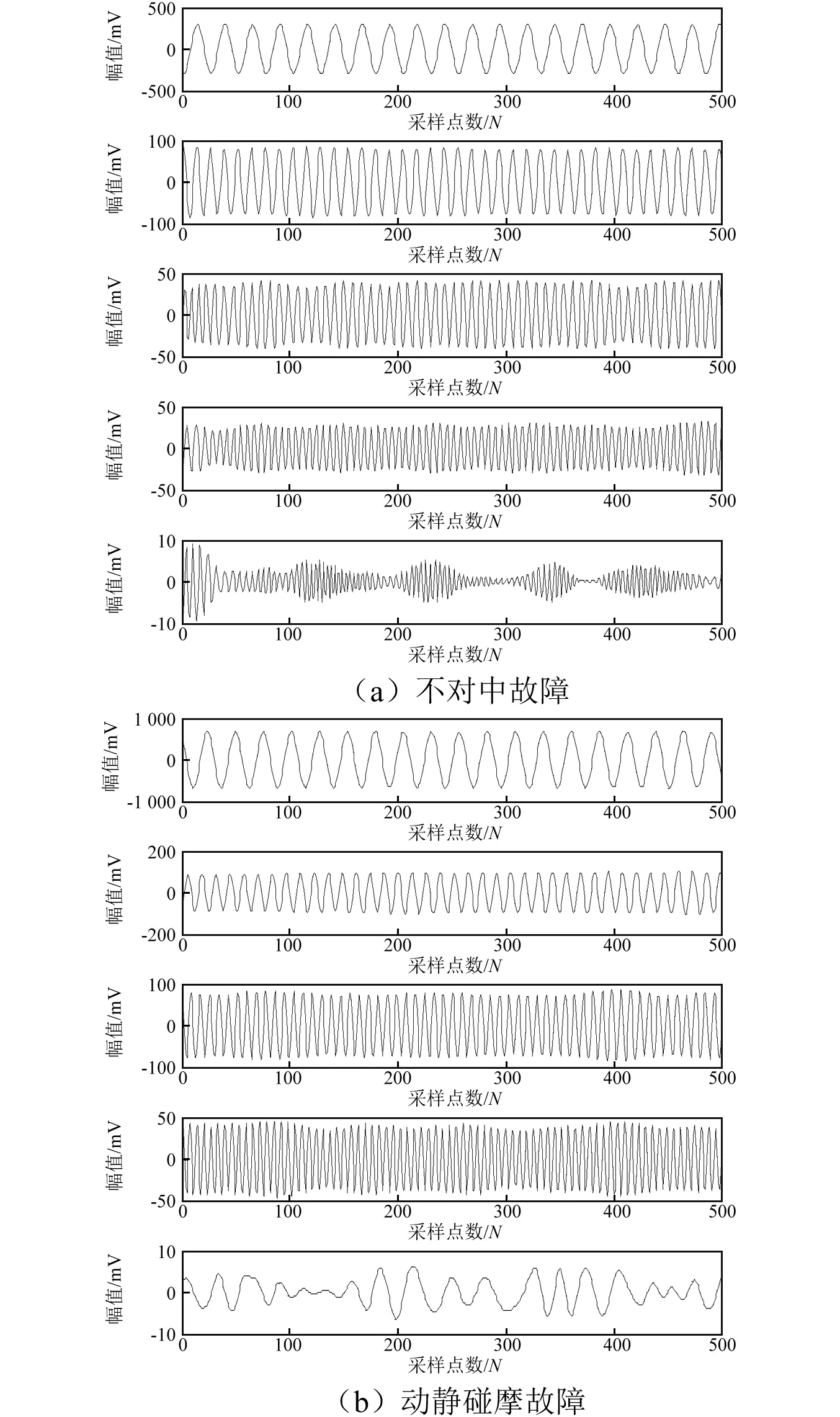
图4 HVD分析结果Fig.4 HVD analysis results

2 基于K-L散度的HVD虚假分量识别方法

为了解决虚假分量问题，使HVD具有更高的工程实用价值，本文对HVD方法进行改进，并最终提出了KL-HVD方法。

2.1 KL-HVD方法

K-L散度，又称为互熵，是信息论中衡量两种概率分布差异的方法[13]。K-L散度值越大，两种分布的差别越大；反之则表示差别越小。设p(x)、q(x)表示两个概率分布，则K-L距离[14]定义为：

(10)

由于K-L距离不具有对称性，不满足真正意义上距离的概念，所以不适合作为衡量p(x)、q(x)差异的定量指标。故选用通过式(11)定义的p(x)和q(x)的K-L散度值作为评价指标：

D(p，q)=δ(p，q) +δ(q，p)

(11)

对于两个信号X={x1，x2，…，xn}和Y={y1，y2，…，yn}，K-L散度值的具体计算方法如下：

(1)计算两信号的概率分布。文中选用非参数估计法[15-16]求解概率分布，定义函数p(x)为信号X概率分布的核密度估计：

(12)

式中：平滑参数h是给定的正数。K(·)是核函数，最常用的核函数是高斯核函数，即

(13)

同理，可以计算出Y的概率分布q(x)。

(2)将p(x)、q(x)代入式(10)求解X和Y的K-L距离δ(p，q)和δ(q，p)。

(3)将δ(p，q)和δ(q，p)代入式(11)即可计算出K-L散度的值D(p，q)。

本文认为真实分量与原始信号的概率分布应该较为相近，二者的K-L散度值较小；而虚假分量和原始信号间的K-L散度值应该相对较大。因此，可以通过设定阈值[17]的方法识别虚假分量。具体步骤如下：

首先，利用HVD方法对原始信号进行分解，得到信号的分量。

然后，计算每个分量和原始信号之间的K-L散度值，并进行归一化处理后得到Di。

最后，通过阈值r实现真实与虚假分量的自动识别，清除虚假分量。

2.2 K-L散度方法与其他方法的对比研究

除K-L散度外，相关系数、互信息等也可以作为两个信号关联程度的评价参数。选定一个有效的评价参数，需要考量其是否能够最大程度上将真实分量与虚假分量区分开。

本节分别采用互信息[19-20]和相关系数法[21-22]识别虚假分量，即利用相关系数、互信息代替本文方法中的K-L散度作为评价参数，并将三者进行实验对比研究。以1.2节中不对中和碰摩信号为例，分别利用K-L散度、相关系数及互信息计算各个分量与原信号间的关联程度，结果见表1、表2。

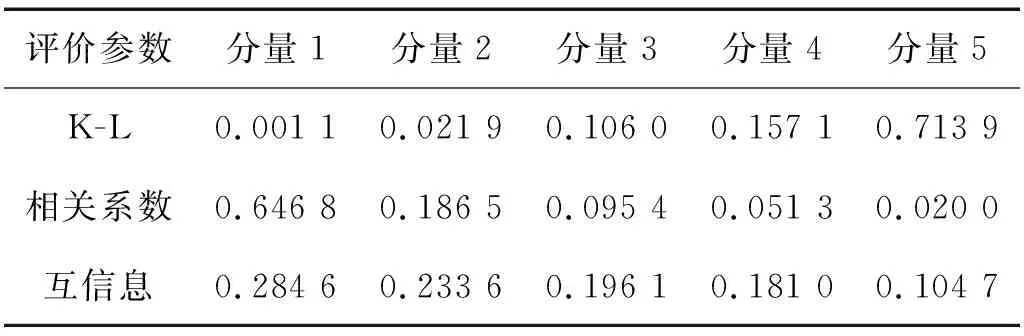
表1 三种虚假分量识别方法结果(不对中)

表2 三种虚假分量识别方法结果(动静碰摩)

从表1、表2可以看出，真实分量的K-L散度值远远小于虚假分量的值。而另外两种评价参数虽然也区分了真实分量和虚假分量，但后两者对于虚假分量的辨别能力明显弱于K-L散度方法。这就表明，K-L散度方法相对于其他方法更能够体现真实成分与虚假分量的差别，基于K-L的虚假分量识别方法具有更好的普适性。

为了区分真实和虚假分量，根据相关学者研究，文献[17]通过设定最大指标值(互信息)的1/10作为阈值，文献[18]设定K-L散度值的阈值为0.01。这种固定阈值的分类方法起到了一定的效果。然而，实际应用中不同信号各个分量的能量分布存在较大变化，固定阈值很有可能出现误诊的现象，同时固定阈值分类方法缺乏理论依据。故本文提出利用聚类的思想对真实和虚假分量自动分类，实现“阈值”的效果。

2.3 高斯混合模型聚类方法

由中心极限定理可知，高斯混合模型(Gaussian Mixture Model, GMM)可以通过组合足够多的高斯分布函数近似任意概率分布[22]。同时，高斯模型均值和协方差形式已知，GMM模型在迭代计算过程中优势显著。因此，本文选用高斯混合模型实现HVD方法中真实分量和虚假分量的聚类识别。

混合高斯模型的定义为：

(14)

式中:K为模型个数；αi为第k个高斯分布的权重系数；N(x|μk,Σk)为第k个高斯分布的概率密度函数，μk,Σk为对应的均值和方差。由于αk,μk,Σk未知，目前较为流形的方法是通过期望最大化算法(Expectation Maximization, EM)对[23]它们进行迭代计算，使样本点在估计的概率密度函数上的概率和最大。

由于概率值一般都很小，对概率取对数，即：

(15)

对式(15)采用EM算法，E步骤是利用模型参数值计算K个高斯模型的权重。模型参数通过初始化或者基于上一步的迭代结果获得。

样本xn由第k个模型生成的概率，即第k个模型的权重为：

(16)

M步骤是基于估计的权值ωn(k)，对模型参数进行迭代。

(17)

(18)

(19)

当算法收敛时即完成了对混合模型的估计。混合模型中各项的结果分别代表样本x属于各个类的概率，概率最大的模型概率极为x的所属类别。

高斯混合模型进行聚类时，一个明显的优势是可以通过计算模型的赤池信息准则(Akaike Information Criterion, AIC)准则量化该模型拟合数据的能力。对原始数据分布拟合的越好，GMM模型的聚类效果也越优异。

AIC准则数的定义式为：

AIC=2k-2ln(L)

(20)

式中:k为模型中独立参数的个数；L为模型的极大似然函数。

2.4 基于GMM的KL-HVD方法阈值研究

针对HVD分解过程中存在的虚假分量问题，本文提出一种基于高斯混合模型的KL-HVD虚假分量识别方法。该方法首先对故障信号进行HVD分解，得到一系列的分量；分别求出每一个分量与原始信号间的KL散度值作为该分量的“指标”：Fi；构建高斯混合模型对所有的Fi进行拟合并通过AIC准则数确定最佳模型形式；最后使用完成训练的GMM模型对HVD分量进行聚类，实现虚假分量自动识别。

聚类法对这些特征向量进行聚类，真实分量与虚假分量自动聚为两类；将原信号中的虚假分量予以消除。该方法整体流程图如图5所示。

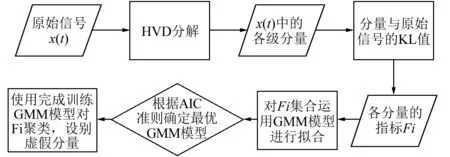
图5 HVD虚假分量识别流程图Fig.5 flow chart of HVD false component identification

3 基于KL-HVD的实验研究

为了验证高斯混合模型作为“阈值”甄别真假分量的有效性，本文选取若干组不同类别的故障信号的HVD分解结果进行聚类。除前文中的不对中与动静碰摩故障信号外，本节增加了油膜涡动和不平衡故障信号。转子油膜涡动和不平衡故障信号的时域图和频谱图见图6、图7。

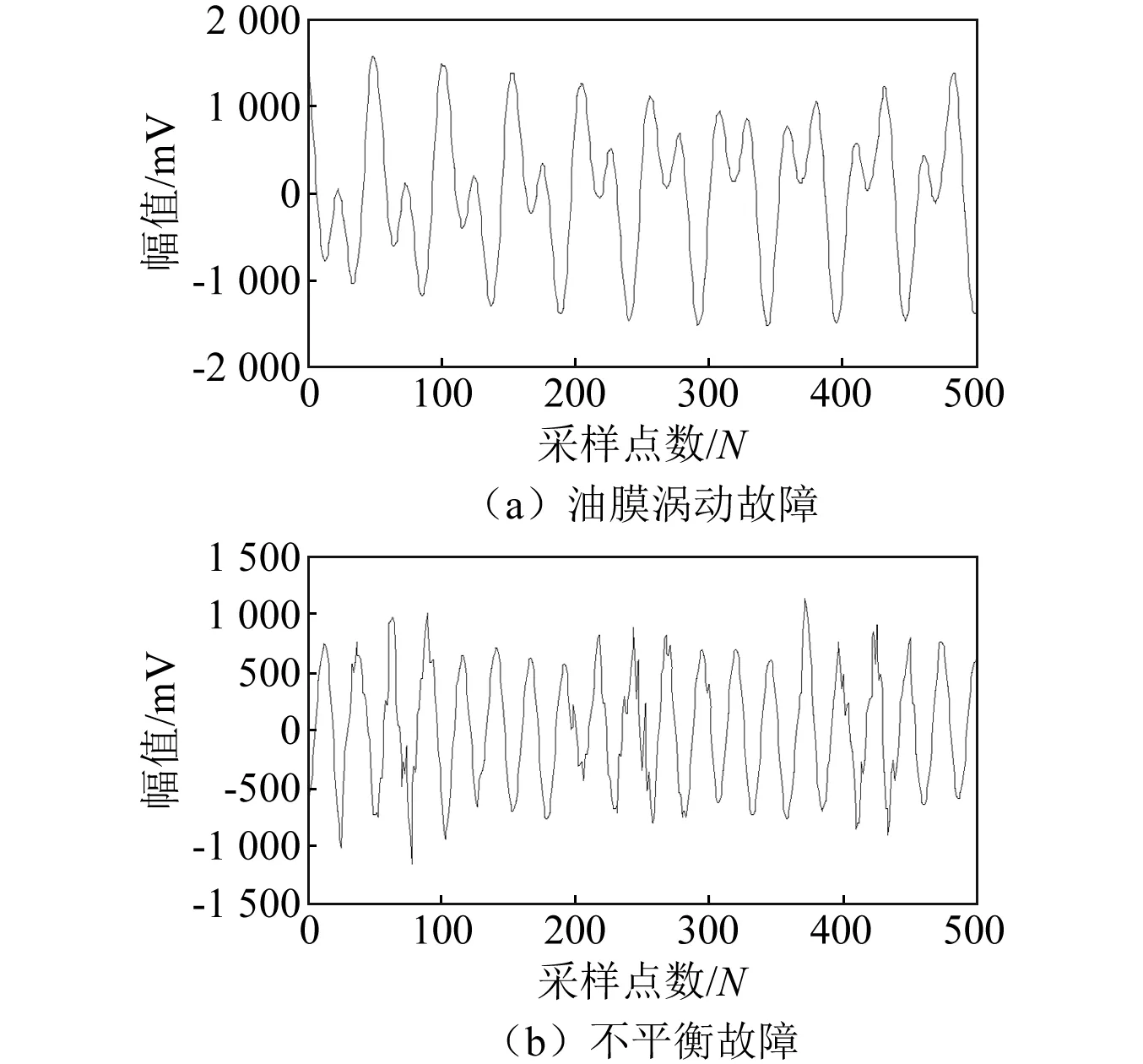
图6 信号时域图Fig.6 signal time domain

图7 信号频谱图Fig.7 signal spectrum

分量1分量2分量3分量4分量5油膜涡动0.001 30.015 30.090 40.309 00.584 0不平衡0.000 10.009 70.097 30.167 00.725 9

从表3可以看出，若选取设定最小K-L散度值的10倍作为阈值，则油膜涡动中的“分量2”将错误识别为虚假信号，若设定K-L散度值的阈值为0.01，则不平衡的“分量2”将错误识别为真实信号，造成虚假分量的错误识别。所以，通过固定阈值的方式识别虚假分量可能会造成误判。

根据三种指标建立GMM模型，模型的聚类结果见表4～6。

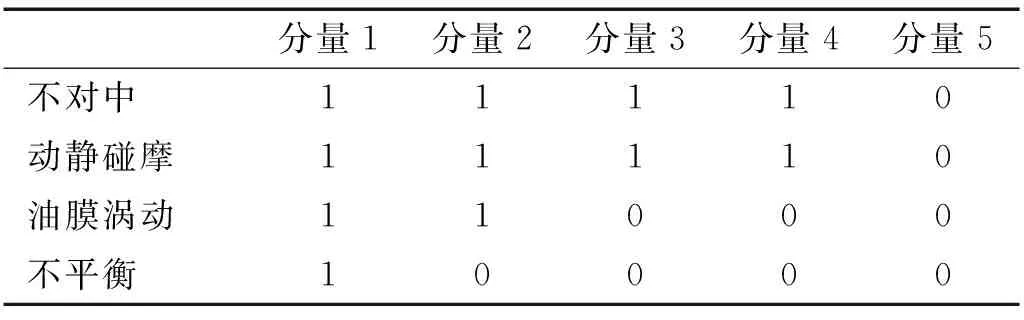
表4 基于K-L散的HVD分量的聚类结果

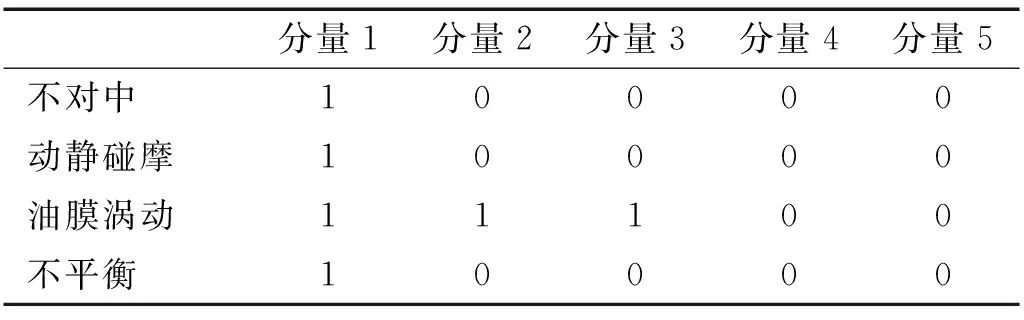
表5 基于相关系数的HVD分量的聚类结果

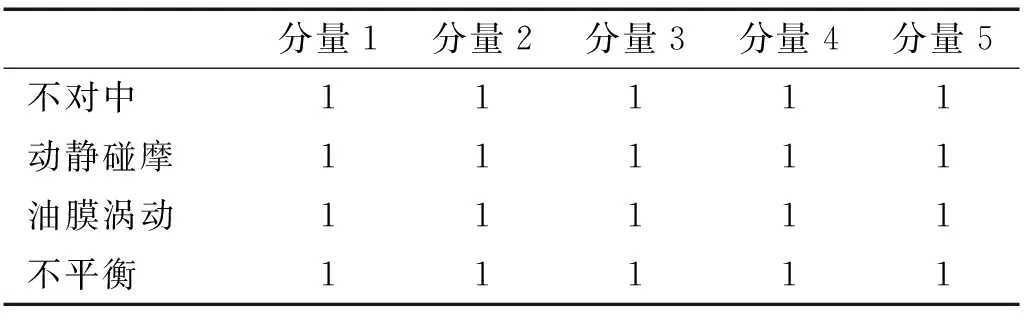
表6 基于互信息的HVD分量的聚类结果

结合表4～6中的分类结果，只有K-L散度指标值的聚类结果是正确的，基于K-L散度值的GMM模型聚类可以准确的清除虚假分量。实验结果验证了本文提出的KL-HVD方法的有效性。为了进一步验证GMM模型聚类效果，本文分别计算了三种模型的AIC值，见表7。

表7 三种GMM模型的AIC值

AIC准则数中的最优模型个数表征了该集合最契合的分类数。从表7中可以看出，互信息指标并不能有效的将HVD分量聚为真实和虚假两类(两个高斯模型)，而K-L散度和相关系数方法的计算结果可以聚为两类。基于AIC准则的计算结果与实验结果一致，故而说明了GMM模型聚类的正确性。

在这里，给出油膜涡动和不平衡两种故障信号的KL-HVD分解结果，见图8。

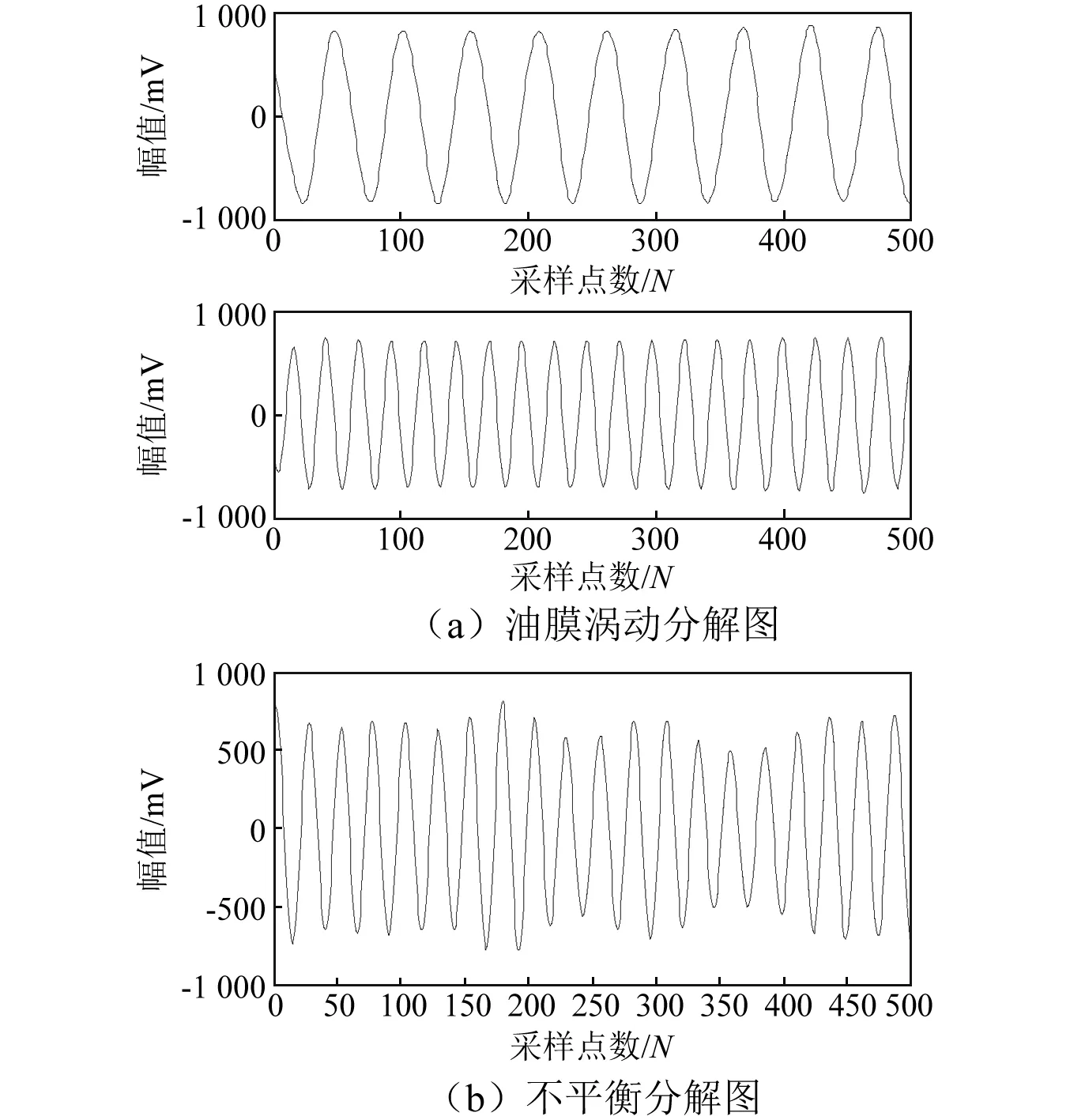
图8 KL-HVD分析结果Fig.8 KL-HVD analysis results

图7(a)中可以看出，油膜涡动的频谱特征体现在半倍频和工频比较突出；图7(b)表明不平衡故障只有工频成分。从图8可以看出，基于KL-HVD方法对信号进行分解后，可以工整的得到信号的各个频段分量，这些分量与图7中的频谱相对应，是信号的真实特征信息。这些分量除包含了信号的频率信息，还清楚地得到各个频段的时域信息，即故障信号的时频特征。KL-HVD方法有效地抑制了虚假分量的出现，更加清晰、准确地提取出振动信号的时频特征。

4 结 论

本文在HVD方法的基础上，针对其虚假分量问题，对其进行改进，最终提出了KL-HVD方法。通过理论及实验研究，得到以下结论：

(1) HVD作为一种新型的信号时频分析方法能够将不同频率信号有效地分离开来，尤其适用于倍频特征明显的转子故障信号。

(2) 作为评价参数， K-L散度相对于其他方法(互信息、相关系数)可以更大程度上体现出真实和虚假成分的差别。基于K-L散度的评价方法更容易鉴别出虚假分量。

(3) KL-HVD方法有效地解决了HVD虚假分量问题，可以更加准确、清晰的分析与提取信号时频特征，是一种具有更高工程实用价值的时频分析方法。