基于改进EEMD的红砂岩声发射信号的频谱特性研究
戴聪聪, 程铁栋, 宗 路, 罗小燕
(江西理工大学 机电工程学院,江西 赣州 341000)
岩石在受到外载荷的作用下,由于内部存在大量的微小裂隙,受力作用后会出现裂隙的闭合、扩展及裂隙间贯通,在整个过程中伴随着部分能量以弹性波的形式释放出来,此现象称为岩石声发射(Acoustic Emission,AE)[1]。通过用仪器检测、记录和分析AE信号,并利用AE信号的特征来推断声发射源的技术称为声发射技术[2]。声发射信号是由多种模式的波组成,而每种模式又是由宽带频率成分波组成,因此声发射波的频带范围比较宽,可从数赫兹到数兆赫兹。声发射源产生的弹性波,由于会受到介质的传播特性以及传感器频率响应特性等影响,在传播过程中会发生反射、折射、衍射、频散等,同时还受到采集环境周围的噪声影响,故传感器所采集到的声发射信号很复杂,因此从复杂的信号中提取声发射源的信息极为重要。目前EEMD算法是对非平稳信号去噪的有效方法之一[3],但EEMD算法也存在一些缺点如:①分解过程中会存在残余的白噪声;②选取有效的IMF分量完全依靠经验来确定。这些都影响了EEMD对信号分解重构的准确性[4]。
随着声发射技术应用于越来越多的领域,对信号的分辨能力、去噪能力以及模式识别等要求都在逐渐提高。黄晓红等[5]应用快速傅里叶分析了砂岩声发射信号的频谱主要分布在10~100 kHz。张艳博等[6]应用HHT方法研究了粉砂岩破裂声发射信号频率特性,得到了粉砂岩破裂分为4个阶段且声发射信号的有效频段为20~120 kHz。凌同华等[7]应用EMD分析了在冲击载荷下岩石声发射信号能量分布特征,得出随着岩石的密度、弹性模量的降低,信号的优势频率越来越集中,而且有往低频发展的趋势。以上应用的方法部分没有有效解决IMF分量的选取问题,因此对岩石失稳现象不能够作出准确判断和预测。
本文针对EEMD算法在以往选取IMF分量存在误判现象提出了一种将EEMD与云相似理论相结合的去噪方法,首先通过模拟仿真分析,并与互相关系数法选取固有模态函数分量做了比较,得出此方法能更好地提高信噪比。然后,将该方法应用于岩石声发射信号的特征提取中,利用选取敏感的IMF分量进行重构,最后结合功率谱法分析了岩石声发射信号的频率特性。
1 改进的EEMD算法
1.1 EEMD算法
Wu等[8]通过研究白噪声信号的统计特性,提出了总体平均经验模态分解EEMD,对信号多次加入不同的白噪声进行EMD分解,根据随机白噪声可以通过多次试验相抵消的特性,将多次分解得到的IMF分量取平均即得到最终的IMF。EEMD算法分解步骤如下:
(1) 将y(t)表示原始信号序列,vi(t)表示第i次实验中添加的具有标准正态分布的白噪声, 即第i次信号为
yi(t)=y(t)+vi(t)
(1)
式中:i=1,2,3,…,I表示实验次数。
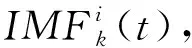
(2)
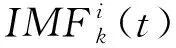
1.2 云相似度理论
云模型由正向云发生器和逆向云发生器组成,是定量数据与定性概念之间的不确定性转换模型, 用C(Ex,En,He)来表示定性概念, 对定性概念C的确定度用u(x)表示。 其中Ex表示期望、En表示特征熵、He表示超熵,它们是云模型的三个数字特征[9]。
如已知样本xi(i=1,2,…,n), 则Ex、En和He的计算步骤如下[10]:
(1) 样本xi的云模型特征期望为
(3)
(2) 样本xi的云模型特征熵为
(4)
(3) 样本xi的云模型特征超熵
(5)
(6)
式中:S为样本二阶中心矩。
云模型中,将定性概念C也记为一个云向量。由此可知,每个时间序列的云向量不同, 将两个i,j不同时间序列的云向量之间的余弦夹角称为两个云向量的相似度为[11]
(7)
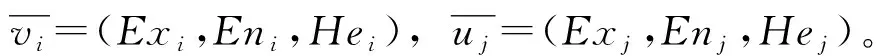
即改进的EEMD算法步骤如下:
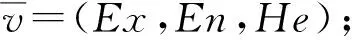
(2) 将原始信号y(t)进行EEMD分解, 得到IMFk(k=1,2,…,n);
(5) 用多次实验统计分析来选取合适的阈值,将大于阈值的IMF分量保留,小于阈值的IMF分量舍去。
2 改进EEMD算法的模拟仿真分析
Mitrakovic等[12]提出了一种连续的声发射信号数学模型,表达式如下
(8)
式中:Ai、ai、fi和ti分别表示第i个信号的幅值、衰减系数、特征频率和峰值时刻。
模拟的AE信号参数取值为:A1=A2=A3=2 v,a1=6.24×108,a2=1.56×108,a3=2.79×108,t1=0.4 ms,t2=0.6 ms,t3=0.8 ms,f1=70 kHz,f2=60 kHz,f3=80 kHz。 在采样频率为f=500 kHz下,没有加入噪声的模拟AE信号的时域波形, 如图1所示。

图1 模拟AE信号Fig.1 Simulation of AE signal
由于采集AE信号的过程中主要是白噪声干扰,所以对模拟的AE信号加入不同信噪比的白噪声,分别为8 dB,10 dB,12 dB。先利用EEMD算法分别对这3个含噪声的AE信号进行分解,再分别计算各IMF分量的云相似度值如统计分布图2所示。EEMD分解算法中加入白噪声的幅度系数为0.15,总体平均次数为200。
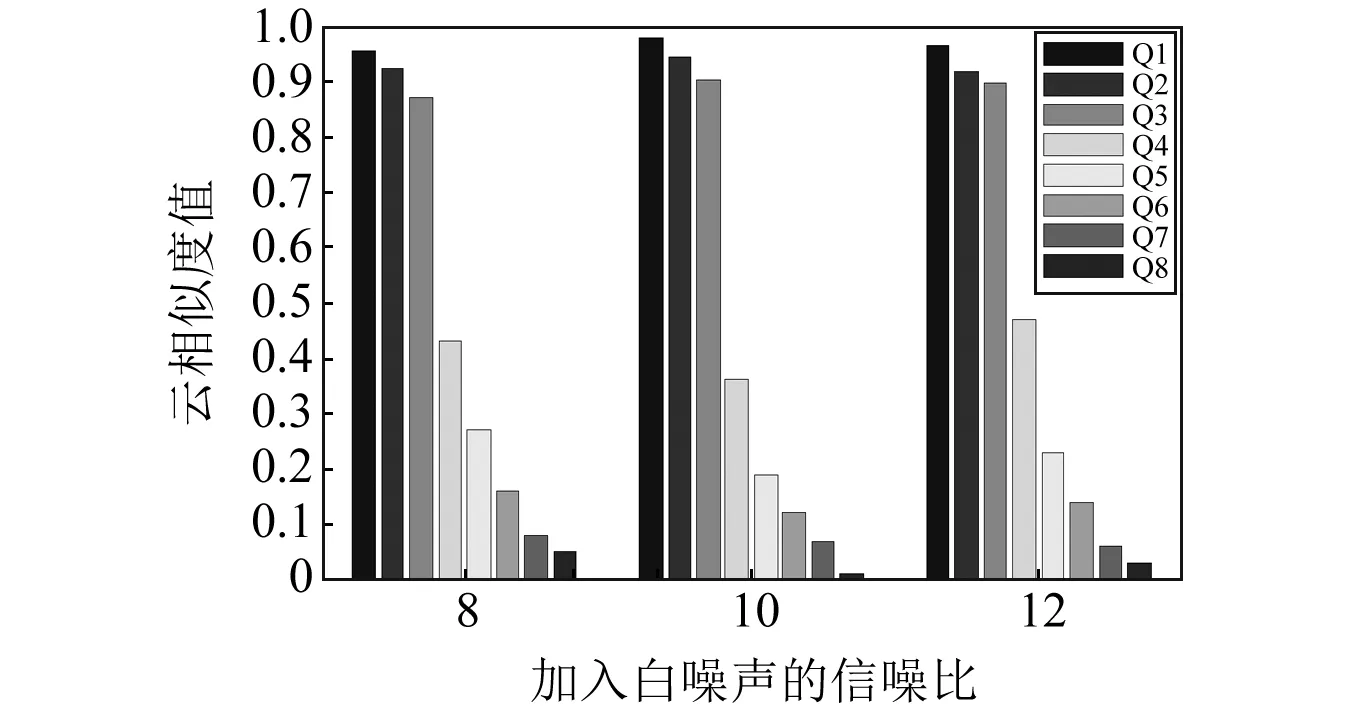
图2 不同白噪声下的各IMF与原始信号的云相似度值Fig.2 The cloud similarity between each IMF and theoriginal signal under different white noises
图2中,Q1~Q8分别表示IMF1~IMF8,由图可以看出,前三个IMF分量云相似度值相对于其它分量较大,说明与原始信号的关联性越强。为了进一步说明云相似度值可以反映各分量与原始信号的关系,取IMF1~IMF6分量组合进行重构并计算信噪比和均方误差,如图3所示。
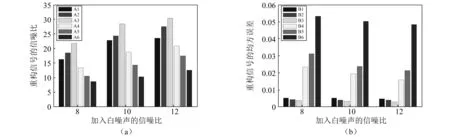
图3 重构信号的信噪比及均方误差图Fig.3 Signal to noise ratio and mean square error of reconstructed signal
图3中A1~A6及B1~B6都分别表示由前6个IMF分量组合重构的信号,如A1、B1表示IMF1重构的信号,A2、B2表示IMF1、IMF2重构的信号,A3、B3表示IMF1、IMF2、IMF3重构的信号,依次类推。由图可知,A3、B3重构信号的信噪比最大且均方误差也最小,即去噪效果最好,更能反映原信号的特征信息,而其它组合重构信号的信噪比较小且均方误差较大,说明与原信号的关联性较小,且与IMF1、IMF2、IMF3的云相似度值存在明显差异,范围为0.521~0.883,因此可选阈值为0.8,将大于该阈值的IMF1、IMF2、IMF3分量作为有效分量保留进行重构。
为了验证改进的EEMD可以达到更好的去噪效果,选取加入白噪声的信噪比为10 dB的信号,将其与互相关系数法选取的EEMD分量进行比较,表1为各IMF与原始信号的相关系数值。

表1 各IMF与原始信号的相关系数
根据相关系数阈值选取的公式[13]
(9)
式中:uh为阈值;ui为第i个IMF分量与原始信号的相关系数; max(ui)为最大的相关系数。根据式(9)可取阈值为0.151 7, 因此,IMF1、IMF2、IMF3、IMF4可作为敏感分量,IMF5、IMF6、IMF7、IMF8可作为虚假分量剔除。两者重构的信号如下图4、图5所示。
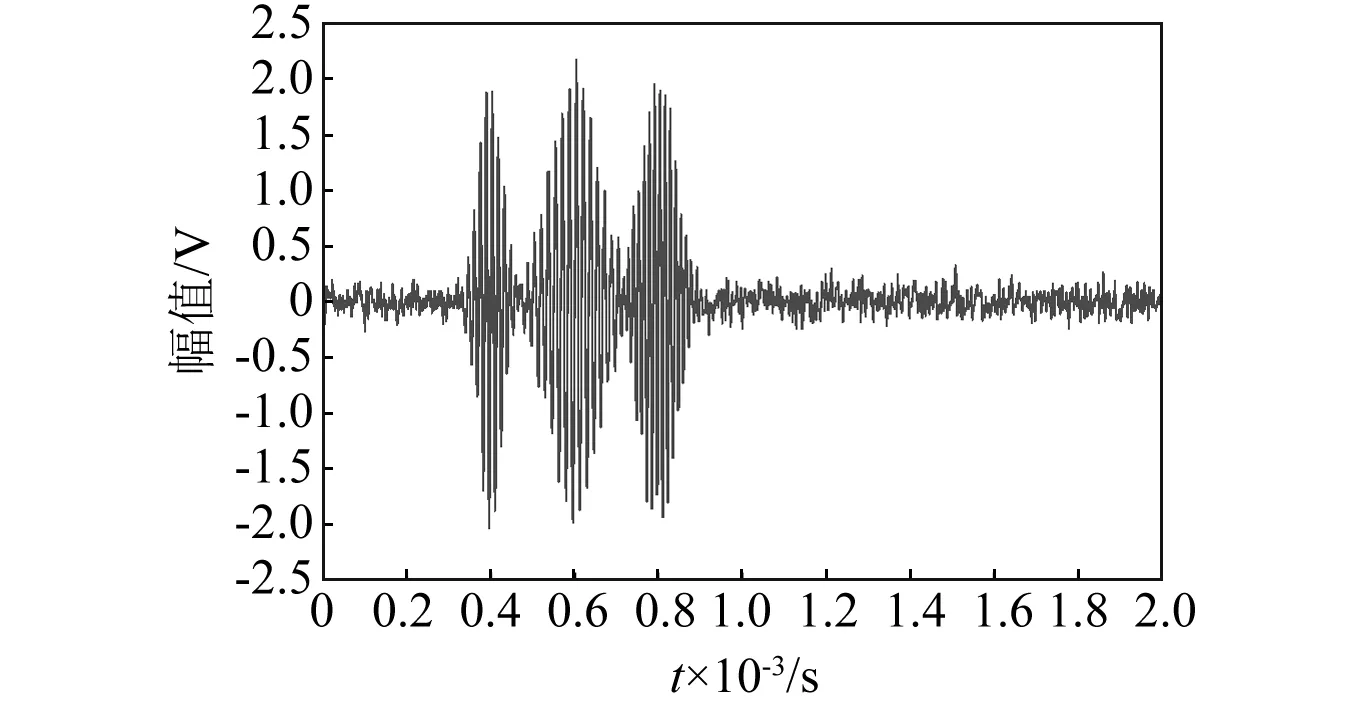
图4 互相关系数法重构的信号Fig.4 The signal reconstructed by the cross-correlation method
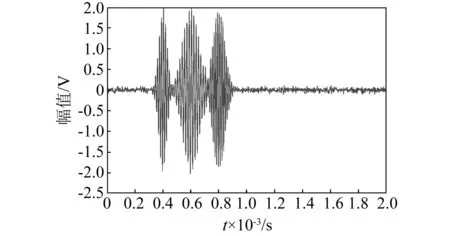
图5 改进EEMD重构的信号Fig.5 Improving the signal for EEMD reconfiguration
比较图4、图5可得,改进的EEMD重构的信号明显比基于相关系数法重构的信号要平滑,且去噪效果更优。为了定量比较,分别计算两个重构信号的信噪比及均方根误差,即基于相关系数法重构的信号的信噪比为18.74,均方根误差为0.019 4,基于改进EEMD重构的信号的信噪比为28.43,均方根误差为0.003 2。因此云相似度法能够正确的选择敏感IMF分量,解决了以往选取有效IMF分量时的误判问题,同时也提高了EEMD算法去噪能力。
3 实验分析
3.1 岩石单轴加载实验方案
声发射实验设备主要由加载系统、声发射采集系统及计算机信息处理系统组成,加载系统采用中国科学院武汉岩土力学研究所研制的RMT-150C型岩石力学试验系统,控制模式为位移加载,速率为0.002 mm/s;声发射采集系统结构框图,如图6所示。

图6 声发射采集系统结构框图Fig.6 Block diagram of acoustic emission acquisition system
传感器采用SR15型,共振频率为150 kHz;前置放大器增益为40 dB,采样频率为0.5 MHz,采样点数为13 330。
本实验岩芯是采用现场套孔应力解除法得到的红砂岩岩芯,加工成直径为φ50 mm、高100 mm的圆柱体样件。为了减少背景干扰噪声及获得更高的信噪比,将声发射传感器探头的接触面涂抹少量的黄油,然后用胶带绑在试样的表面居中位置,如图7所示。

图7 加载试验装置图Fig.7 Loading test device diagram
3.2 敏感IMF分量选择及特征提取
试件安装好后,设置好参数开始试验,采集试验所需的数据。试验时采集了多组信号,现取每次试验声发射起始点的信号进行分析,时域波形及功率谱分析,如图8、图9所示。
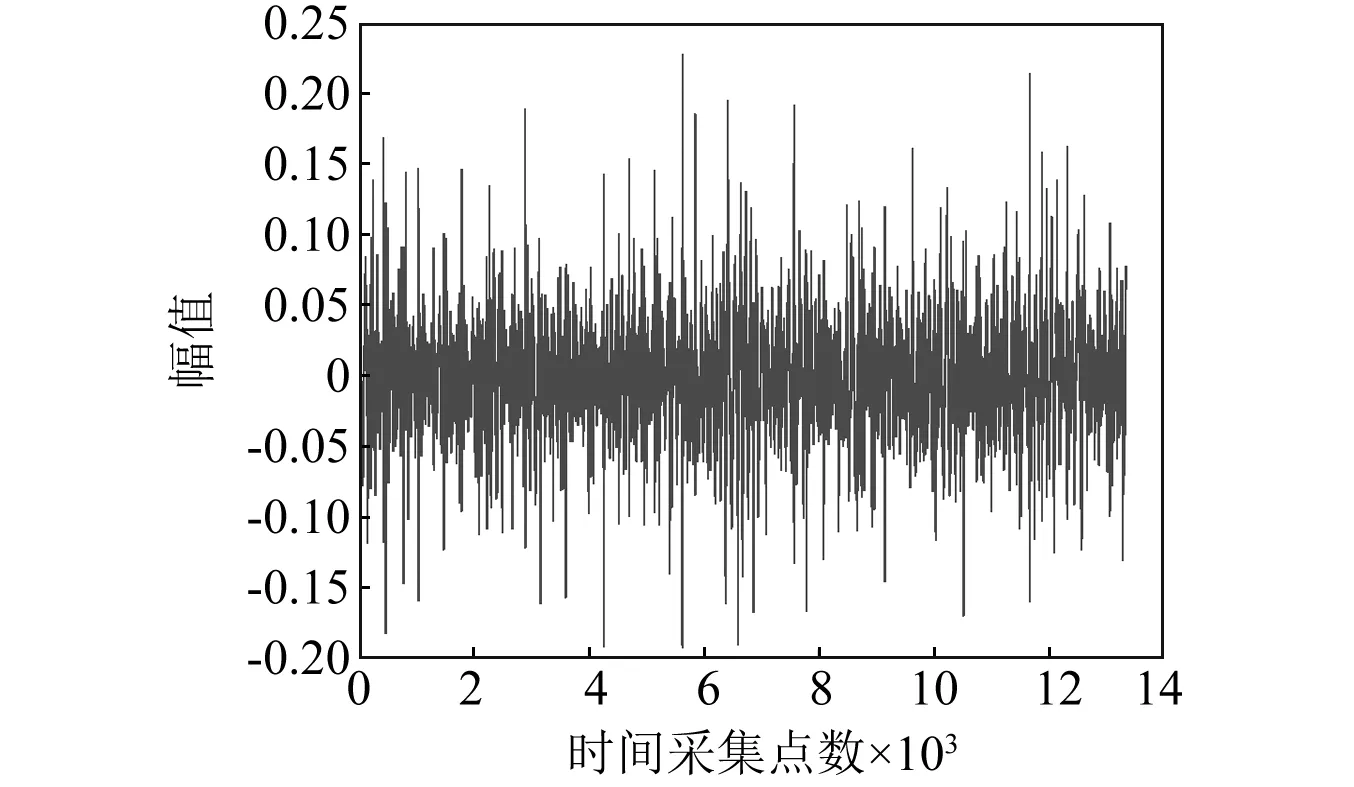
图8 声发射时域波形图Fig.8 Time domain waveform of AE
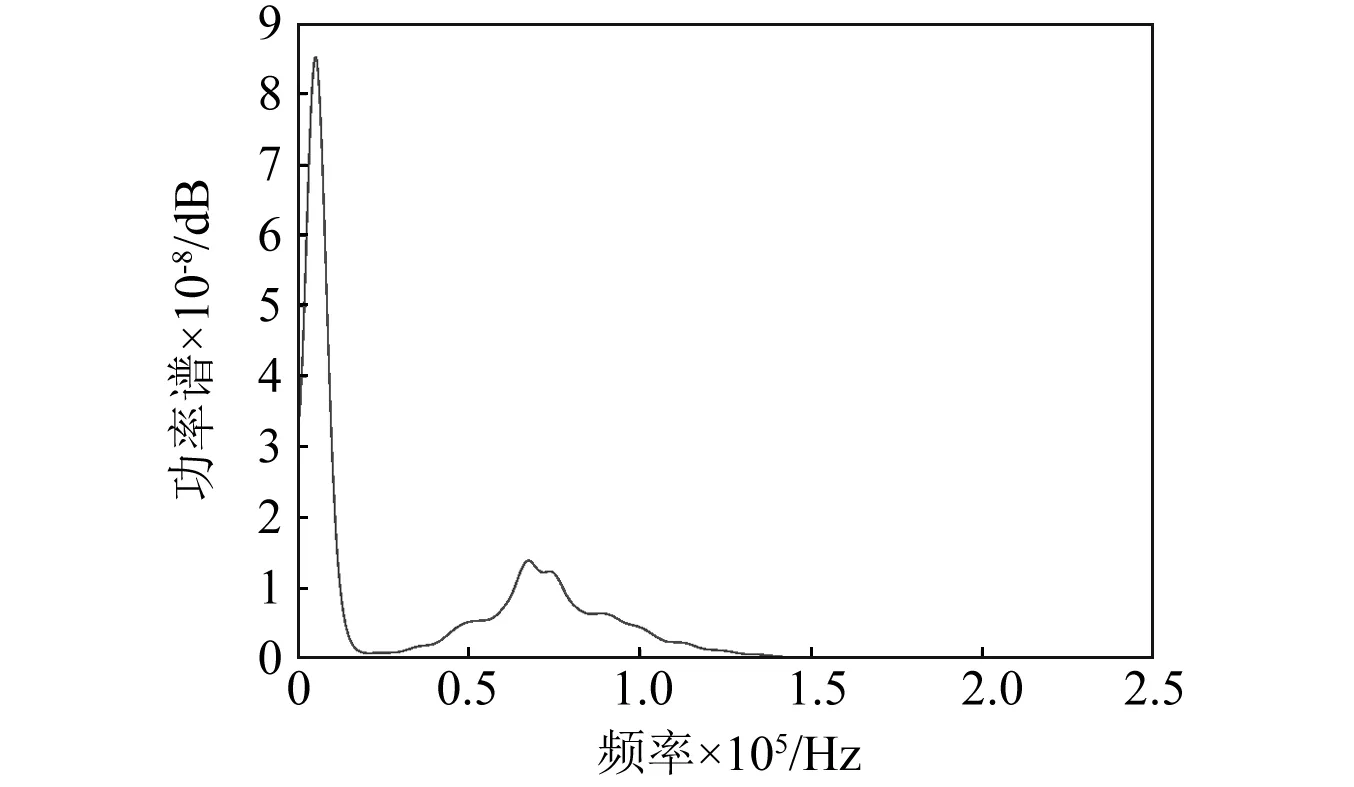
图9 功率谱分析图Fig.9 Power spectrum analysis
从图9中可以看出,声发射信号分为两个频段0~25 kHz,25~150 kHz。
采用改进的EEMD算法对岩石声发射时域波形进行分解,分解结果取前8个如图10所示。
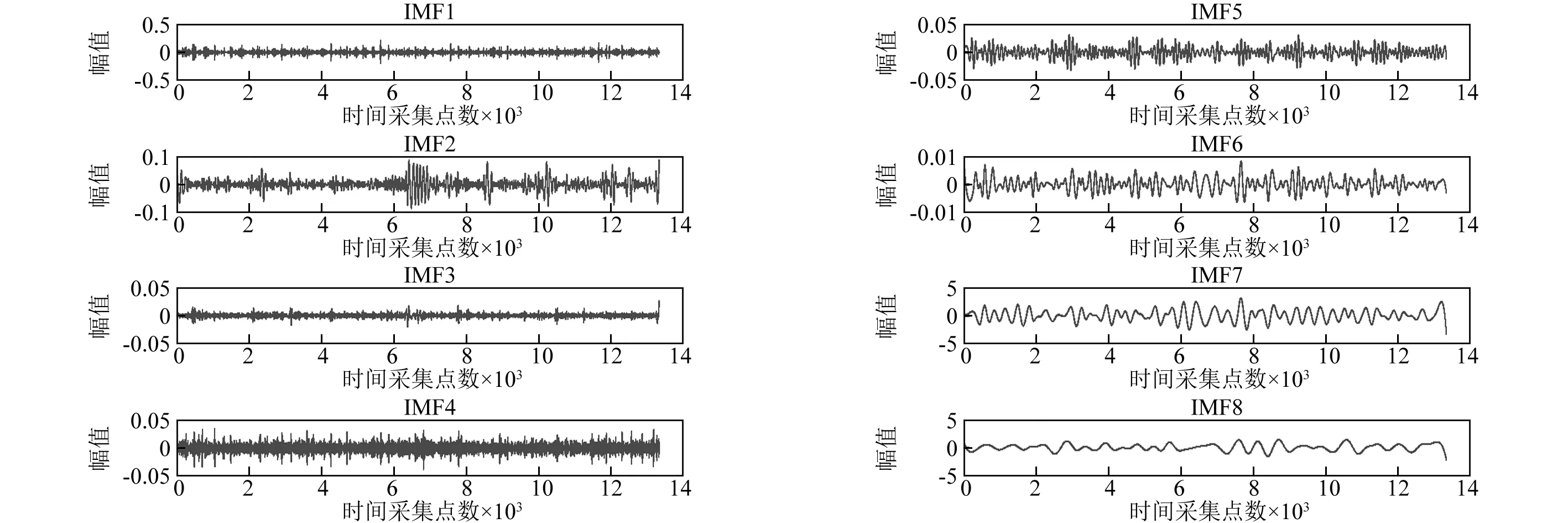
图10 岩石声发射信号的前8个IMF波形Fig.10 The first 8 IMF waveforms of rock acoustic emission signals
由图10中可以看出IMF5、IMF6、IMF7、IMF8分量是原始信号中分解出的时间尺度最长、频率较低的分量,代表信号中的低频成分。运用云相似度法计算被分解出的IMF1~IMF8与原始信号的云相似值,得到云相似度值如表2所示。

表2 IMF1-IMF8与原始信号的云相似值
在表2中,simq(q=1,2,…,8)分别表示IMFn(n=1,2,…,8)与原信号的云相似值。从表中可以看出,IMF4、IMF5、IMF6、IMF7、IMF8的相似值与其他IMF分量的云相似度值存在明显的差异,差值范围为0.346~0.906。为了进一步观察云相似度值的分布规律和阈值选取的普遍性,取10组岩石声发射信号分别经改进的EEMD分解,然后计算分解出的各分量与原始信号的云相似值,都取前6个分量的云相似值进行曲线拟合,如图11所示。
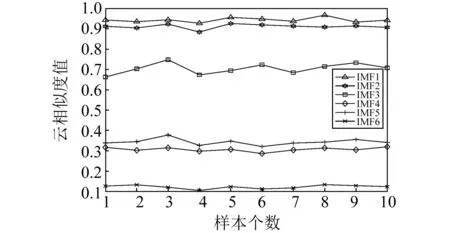
图11 所有样本的云相似值拟合曲线图Fig.11 Fitting curves of cloud similarity values for all samples
从图11中可以得知,IMF1、IMF2、IMF3虽然都有一定的波动,但所有值都很大,说明含有原始信号的信息量更多,关联性更强,可以完全反映原始信号的特征。而IMF4、IMF5、IMF6的值相对较小,说明是与原始信号无关的噪声。根据多次实验统计分析,因此可选阈值为0.655。
利用前三个分量进行重构,并分析重构信号的功率谱,如图12、13所示。
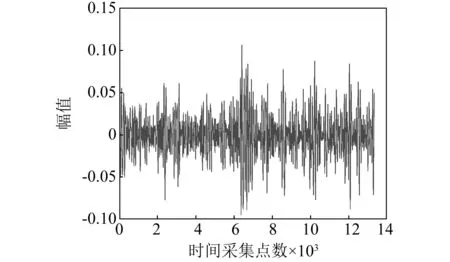
图12 重构的岩石声发射信号Fig.12 Acoustic emission signal of reconstructed rock

图13 重构信号的功率谱图Fig.13 Power spectrum of reconstructed signal
从图8与图12中可以明显看出大部分噪声已经被滤除,原始声发射信号的特征也比较明显。比较图9和图13可知,在75 kHz左右的幅值变化不大,而0~25 kHz的频段几乎为零,故可将0~25 kHz对应于IMF4、IMF5、IMF6、IMF7、IMF8低频分量,而25~150 kHz可对应于IMF1、IMF2、IMF3高频分量。因此,红砂岩声发射信号的有效频率范围为25~150 kHz。
4 结 论
(1) 本文提出了一种改进的EEMD算法,即用云相似度法来选取敏感的IMF分量,并与基于相关系数法选取的固有模态函数进行比较,分析了各自选取分量重构信号的信噪比及均方误差,得出该方法能更好的达到去噪效果,克服了以往在选取敏感分量上存在误判的现象;
(2) 将该方法应用到岩石声发射信号处理中,经过改进EEMD分解,计算各分量与原始信号的云相似度值,其信号的能量主要分布在前三个分量,并经过多组实验统计分析,进而选取阈值为0.655;
(3) 实验结果表明:改进的EEMD对红砂岩声发射信号降噪是一种有效的方法,将0~25 kHz对应的IMF4、IMF5、IMF6、IMF7、IMF8低频分量作为噪声滤除,而25~150 kHz对应的IMF1、IMF2、IMF3高频分量作为敏感分量进行保留,并最后得出红砂岩破裂过程的声发射信号的有效频段为25~150 kHz,与砂岩声发射信号的频率大致对应,为选出相应工作频率的声发射传感器提供依据,对声发射源信号的定位及失稳预测具有重要意义。

