主成分分析和长短时记忆神经网络预测水产养殖水体溶解氧

陈英义，程倩倩，方晓敏，于辉辉，李道亮



主成分分析和长短时记忆神经网络预测水产养殖水体溶解氧

陈英义1,2，程倩倩1,3，方晓敏1,3，于辉辉1,3，李道亮1,2

（1. 中国农业大学信息与电气工程学院，北京 100083；2. 农业部农业信息获取技术重点实验室，北京 100083；3. 北京农业物联网工程技术研究中心，北京 100083）

为了提高水产养殖溶解氧预测的精度，提出了基于主成分分析（principal component analysis, PCA）和长短时记忆神经网络（long short-term memory，LSTM）的水产养殖溶解氧预测模型。首先通过主成分分析提取水产养殖溶解氧的关键影响因子，消除了原始变量之间的相关性，降低了模型输入向量维度；然后，在Tensorflow深度学习框架的基础上建立LSTM神经网络的水产养殖溶解氧预测模型；最后，利用该模型对浙江省淡水水产养殖研究所综合实验基地某池塘溶解氧进行验证。试验结果表明：该模型与BP神经网络等其他浅层模型相比，模型评价指标平均绝对误差、均方根误差和平均绝对误差分别为0.274、0.089和0.147，均优于传统的预测方法；该模型具有良好的预测性能和泛化能力，能够满足水产养殖溶解氧精确预测的实际需要，可以为水产养殖水质精准调控提供参考。

水产养殖；溶解氧预测；主成分分析；LSTM神经网络；循环神经网络

0 引 言

水产养殖溶解氧含量是反映水产品生长状况、水质状况的重要指标[1]，易受温度、风速、风向、雨量、水生生物新陈代谢以及人为活动等多种因素的影响[2]，且具有非线性、大时滞和不稳定等特点。因此对水产养殖溶解氧预测方法进行研究，及时准确掌握未来溶解氧的变化规律，对于预防水质恶化与疾病爆发，减少养殖风险、优化养殖管理具有重要意义。

目前，国内外学者针对水质溶解氧预测方法已经进行了大量的研究[3-5]，取得了一定的成果。如徐敏等[6]提出基于混沌理论、相空间重构思想和嵌入理论的预测模型对于河流溶解氧预测；朱成云等[7]建立了基于混沌变异的分布估计算法优化最小二乘支持向量机模型对工厂化水产养殖溶解氧预测分析；刘双印等[8]采用了蚁群算法优化最小二乘支持向量机对河蟹养殖溶解氧进行预测；宦娟等[9]构建了基于K-means聚类和极限学习机（extreme learning machine, ELM）神经网络的养殖水质溶解氧预测模型。上述涉及的预测方法均属于浅层结构的机器学习方法，在处理大数据上缺少鲁棒性，导致模型普遍缺乏长效性和扩展能力，不能完全反映数据的本质特征。

近年来，基于深度学习的预测方法得到广泛应用[10-11]。此方法可以实现高维函数的逼近，挖掘出蕴藏于数据中的隐含信息，具有强大的高度抽象化特征能力，与浅层结构的机器学习方法相比具有更强的数据学习能力和泛化能力[12]。在众多深度学习模型中，循环神经网络（recurrent neural network, RNN）将时序的概念引入到网络结构设计中使其在时序数据分析中表现出更强的适应性[13-14]。LSTM神经网络，作为RNN的变种模型，可以有效地解决RNN训练时存在梯度消失和梯度爆炸等问题，大大提高了RNN网络的准确性[15]。陈卓等[16]提出了基于LSTM神经网络的电力负荷预测方法，预测效果很好；于家斌等[17]构建了基于LSTM神经网络的蓝藻水华预测模型，实现了对水华发生的精准预测；王鑫等[18]利用LSTM神经网络对故障时间序列数据进行预测，验证了模型的精确性。然而利用LSTM神经网络对水产养殖水质参数预测的相关研究较少。

因此，本文在与BP神经网络、PSO-BP神经网络、ELM、LSSVM等传统模型进行对比的基础上，提出并构建了基于PCA-LSTM神经网络的预测方法，以期探索出较好的方法用于提高溶解氧预测精确度。并采用浙江省淡水水产养殖研究所综合试验基地养殖池塘采集到的水质参数展开试验。

1 数据获取与预处理方法

1.1 试验区域

试验数据样本采集自浙江省淡水水产养殖研究所综合试验基地。该基地位于湖州市吴兴区八里店现代农业综合开发区内（120.197 3N, 30.805 9E），面积约33.3 hm2，是集“水产选育种、优质苗种繁育、健康养殖试验基地及内陆水域增殖放流中心”等功能为一体的综合性基地。选取的池塘长为32 m，宽为32 m、水深约1.2 m，养殖品种为杂交鲌鱼，并且池塘中央安装了一个叶轮式增氧机进行增氧。

1.2 数据源及数据预处理

采用自动监控传感器和手持传感器相结合的方式采集试验池塘溶解氧等水质参数。池塘中央，选取同一平面的4个点位放置监控传感器，数据实时上传至水产养殖智能监控平台；池塘四周，选取16个点位，使用手持传感器现场记录水质参数；同时在池塘的东北角位置搭建便携式气象站，实时在线采集雨量、风速、风向、太阳辐射、空气温度、空气湿度、大气压强、土壤水分、土壤温度生态环境数据，试验中所使用的采集设备及现场照片如图1所示。采集周期为2017年7月8日至8月8日，每10 min采集1次。因篇幅有限，仅展示采集的2017年7月17日部分原始数据如表1所示。

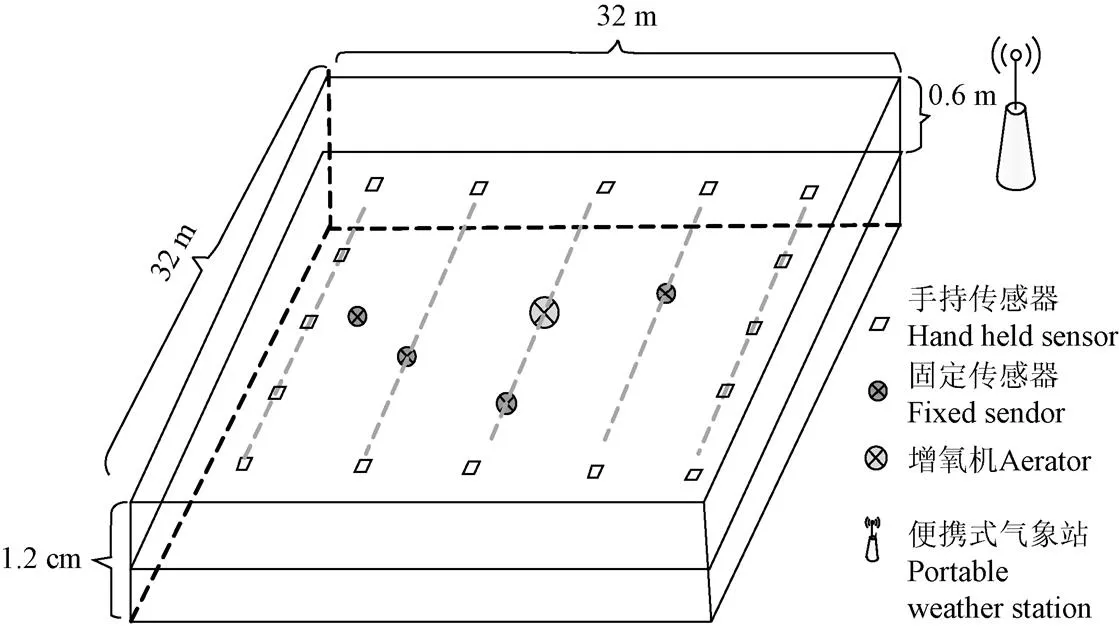
图1 池塘水质监测立体示意图

表1 2017年7月17日采集的部分原始数据

由于设备故障、网络不佳、恶劣环境以及人为因素等影响，传感器采集所得的原始数据难免出现数据缺失、数据异常等情况。这样的数据称为“脏数据”，“脏数据”会导致数据处理成本和相应时间的增加。此外，不同量纲的数据序列也会影响最终模型的预测性能。因此，在进行模型研究前针对前后时间间隔不大的缺失数据现象[19-20]，采用式（1）线性插值的方法对其进行修复处理；若丢失数据较多或时间间隔较大，则采用天气类型相同或对相近相邻几天中同一时刻的数据来填补；对出现的异常数据采用式（2）均值平滑法进行水平处理和式（3）均值法进行垂直处理；并采用式（4）对数据进行归一化处理。

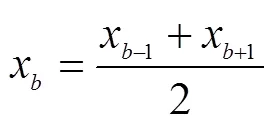
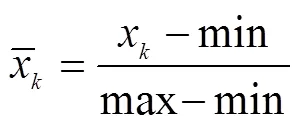
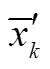
2 预测模型构建

2.1 主成分分析法

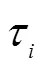
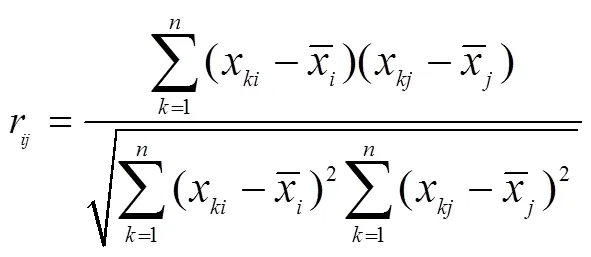
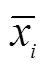
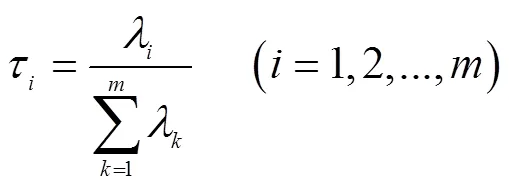
其中，选取主成分的个数取决于主成分的累计贡献率，用于表示综合变量解释原始变量的能力。累计贡献率越大说明数据信息损失越小；5）计算主成分载荷矩阵以及主成分得分。其中载荷矩阵表示原始数据的协方差矩阵的特征值。

最后，将原始样本数据带入主成分的表达式中即可计算出主成分得分。

2.2 长短时记忆神经网络

LSTM神经网络可以从经验中学习分类，更好地对长短时依赖进行表达。目前，LSTM神经网络已经成为RNN甚至深度学习框架中热点的研究模型，并且在手写字符识别、语音识别和机器翻译等领域获得了很好的效果，引起了广泛的关注[22]。循环神经网络是一类允许节点连接成有向环的人工神经网络。RNN网络可以看作是一个所有层共享相同权值的深度前馈神经网络，包含输入层、输出层和隐藏层，分别用向量序列(1,…,x)，(1,…,o)，(1,...,)表示。隐含层和输出层的计算公式为

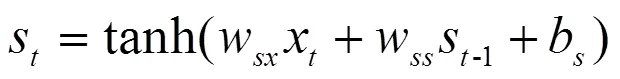
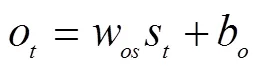
式中w、w和 w分别指输入层和隐含层、隐含层和隐含层以及输出层和隐含层之间的权重矩阵。b和b均表示偏差。为网络权值，所有层次共享同一参数，tanh为双曲线正切激活函数。

理论上，RNNs能够对任何长度的序列数据进行处理，实际中，如果序列过长会出现梯度消失和梯度爆炸的问题。除此之外RNN难以保持较长时间的记忆。而LSTM网络的出现有效地解决了这些问题。LSTM网络不仅具有传统循环神经网络的功能，而且LSTM网络采用特殊的控制单元，解决了误差信号消亡的问题[23]。经过不断的改进，目前广泛应用的LSTM模型存储单元的基本架构如图2所示。

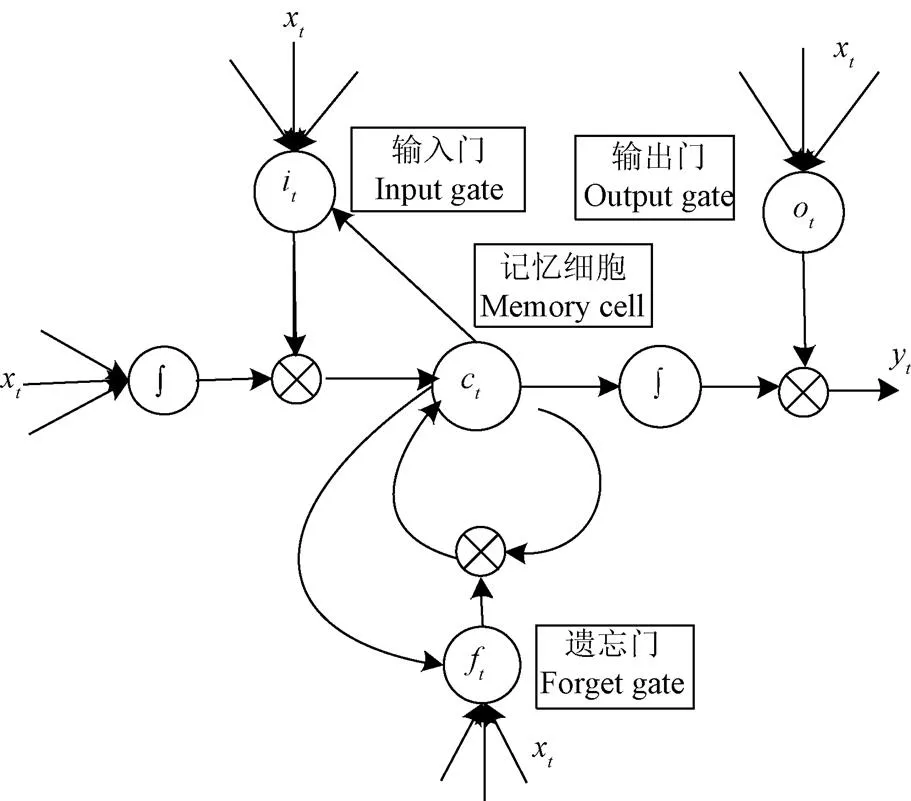
注：xt、yt分别为输入和输出序列，it、ft、ct和ot为t时刻的输入门、遗忘门和输出门，∫为激活函数。

主要包括输入门、输出门、遗忘门和细胞状态。遗忘门确定需要从从细胞状态中忘记哪些信息；输出门确定将要更新哪些信息到细胞状态中；输出门确定将要输出哪些信息。这3个门是控制信息流的关键。整个存储单元计算过程可以用如下公式表示

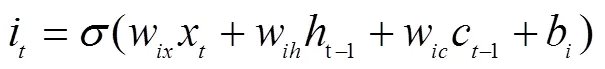
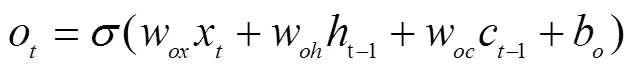
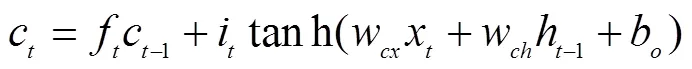
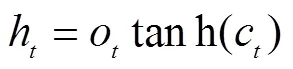
式中i、f、o分别为时刻输入门、遗忘门和输出门的计算方法；c为时刻记忆细胞的计算方法；h为时间点LSTM单元的所有输出。和tan分别表示sigmoid和双曲正切激活函数。和表示相应的权重系数矩阵和偏置项。LSTM模型训练的具体流程为1）根据公式（6）－（10）计算LSTM存储单元的输出值；2）计算每个LSTM存储单元的误差项，包括时间和网络层级2个反向传播方向；3）结合相应的误差项，计算每个权重的梯度；4）采用梯度优化算法，本文选用的适应性动量估算法，更新权值。

2.3 基于PCA_LSTM神经网络的溶解氧预测模型

基于上述算法，为了提高预测模型的精度，本文将2种算法相结合，构建了基于PCA-LSTM的水产养殖溶解氧预测模型。其预测流程如图3所示，主要包括水质数据获取及数据预处理、溶解氧关键影响因子筛选、基于LSTM神经网络的预测模型训练、模型测试和模型应用，具体的水产养殖溶解氧的预测过程如图3。

图3 基于PCA-LSTM的水质溶解氧预测流程图

1）通过水质在线检测系统和小型气象站获取水产养殖水环境数据和当地的气象数据，并对采集到的数据进行修复和归一化预处理；

2）利用PCA筛选出水产养殖溶解氧的关键影响因子，降低模型输入参数的维度，消除了变量之间的冗余性和相关性，并划分相应的样本训练集和测试集；

3）初始化预测模型的参数，将训练样本数据集输入模型，不断调整模型参数，直到获取目标准确率，构建基于PCA-LSTM的水产养殖溶解氧预测模型；

4）采用测试集测试水产养殖溶解氧预测模型性能，与其他传统预测模型对比分析，实现对未来某一时刻的水产养殖溶解氧含量的精确预测。

2.4 模型评价指标

使用预处理后的数据作为模型的输入，对基于PCA-LSTM的预测模型进行训练和测试。本文选用的预测模型性能评价指标有平均绝对误差（MAE），均方根误差（RMSE）和平均绝对百分误差（MAPE）。如下，公式（16）为MAE的计算公式，公式（17）为RMSE的计算公式，公式（18）为MAPE的计算公式。

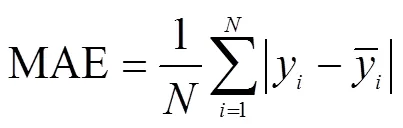
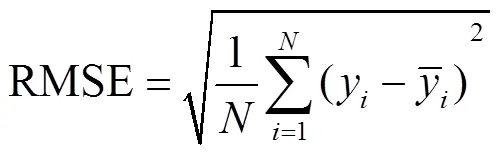
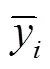
3 结果与讨论

3.1 试验准备

试验之前，我们首先介绍试验中所选用的数据集，与本文提出的PCA-LSTM模型相对比的其他预测模型，试验运行平台和软硬件环境，评价了对不同预测模型优劣精度度量指标。

3.1.1 数据集

本节以浙江省淡水水产养殖研究所试验基地某试验池塘中的溶解氧为研究对象。采用已经预处理过的试验数据，主要包括水温、pH值、溶解氧、风速、风向、太阳辐射、空气温度、空气湿度、大气压强、土壤湿度和土壤温度等水产养殖生态环境数据。最终实现2 h后的溶解氧含量预测，在线采集到的5 007条样本数据作为数据源，利用K折交叉验证法验证和测试模型性能[24]，其基本思想是将原始数据分为份，然后取-1份为训练集，余下的1份作验证集，首先用训练集对模型进行训练，再利用验证集来测试训练得到的模型。上述过程重复次，最后利用次验证集上的模型精度的平均值作为评价模型的性能指标。

3.1.2 对比模型

除了与单一的LSTM预测模型对比，本文还将PCA-LSTM模型与以下4种浅层模型进行试验对比。

1）BP （back propagation, BP）神经网络

BP神经网络在复杂的非线性系统中具有较高的建模能力，并对数据具有良好的拟合能力，在预测方面应用广泛。研究表明，这种简单的网络结构可以逼近任意非线性的函数，是一种典型的函数映射之间的关系[25]。

2）粒子群优化BP神经网络

BP神经网络存在容易陷入局部极值、稳定性差、收敛速度慢等问题，因此目前很多研究着将智能算法加入BP网络中，以达到优化[26]。粒子群算法（particle swarm optimization, PSO）通过不断地更新速度和位置实现优化到全局最优解，不依靠梯度信息，可调参数少，算法实现容易且运行效率高，具有良好的全局搜索性能，利用个体间的协作和竞争实现全局搜索，减少了陷入局部最优解的风险，鲁棒性强。因此利用PSO优化BP神经网络的初始权值和阈值，能够改善网络的性能，增强泛化能力，提高预测精度。

3）极限学习机

ELM（extreme learning machine, ELM）是一种简单易用、有效的的单隐层前馈神经网络[27]。与传统的前馈神经网络训练速度慢，容易陷入极小值点，学习率的选择敏感等缺点，ELM算法随机产生输入层与隐含层的连接权值及隐含层神经元的阈值，且在训练过程中无需调整。只要设置隐含层神经元的个数，便可以获得唯一的最优解，具有学习速度快、泛化能力好等优点[28-29]。

4）最小二乘支持向量机

最小二乘支持向量机（least squares support vector machine, LSSVM）采取结构风险最小原则，有效提高了求解速度和噪声能力，在解决小样本、非线性等问题中表现出色[30]。它扩展了SVM（support vector machine, SVM）的形式，并保留了SVM结构风险最小化和小样本等优点，对SVM模型进行优化，将SVM中的损失函数替换成最小二乘损失函数，不等式约束条件替换成等式约束条件，使求解过程由二次寻优问题转化为线性方程组的求解，简化了求解过程、提高运算效率[31]。

3.1.3 平台和环境

试验所使用计算机的配置如下：处理器为AMD A8-4500M，CPU频率为2GHz；内存为4.00GB；操作系统为Windows 7（64-bit）；程序设计语言为python 3.5（64-bit）和MATLAB 7.11.0（64-bit），集成开发环境为Anaconda 3和MATLAB R2010b。程序设计中，LSTM模型由基于Anaconda的tensorflow 1.2.0程序包实现，BP神经网络、PSO-BP神经网络、极限学习机和最小二乘支持向量回归均结合MATLAB所提供的工具箱并完成相关程序的编写。

3.2 试验结果分析

3.2.1 仿真分析

使用小型气象站采集到的气象因子较多，它们之间存在一定的相关性，直接作为模型的输入会使网络结构过于庞大，所以使用主成分分析法对池塘养殖环境数据降维和分析，得到不相关的新变量，最终提取出养殖池塘溶解氧的关键影响因子。本文利用SPSS软件实现对溶解氧关键影响因子的筛选，方差及主成分贡献率如表2所示。选择“特征值”大于1的成分作为提取主成分的原则，表2中可以直观看出，前3个因子的特征值均大于1，因此选择前3个因子代替原变量。采用具有Kaiser标准化的正交旋转法得到各个环境因子对不同主因子的因子载荷，得到的成分矩阵如表3所示，对第1因子贡献最大的有太阳辐射和土壤温度；第2因子贡献较大的是风速和溶解氧，风向和土壤水分对第3因子贡献较大。

表2 方差及主成分贡献率

表3 成分矩阵

因此本文选用的关键影响因子有水温、太阳辐射、风速、风向、土壤温度和土壤水分和溶解氧，也与养殖领域专家凭借经验选取水质溶解氧的关键影响因子基本一致，降低了数据维度和复杂度，并以此构建未来某一时刻溶解氧预测模型的输入样本，输出参数为2 h后的溶解氧含量。由于所使用的计算机配置不足，为了提高训练速度，抽取其中的1 000条数据作为样本数据集，并采用5折交叉验证方法对模型精度进行评估。

首先，选取2.3节提出的方法建立水产养殖溶解氧预测模型。采用Adam算法进行优化，迭代次数为2 000次时，其中输入层节点数为7和输出层节点数为1，5次试验所对应的隐含层节点数、学习率、批尺寸和时间步的值如表4所示。图4为5折交叉验证后训练PCA-LSTM模型得到的5组误差曲线和预测趋势图。

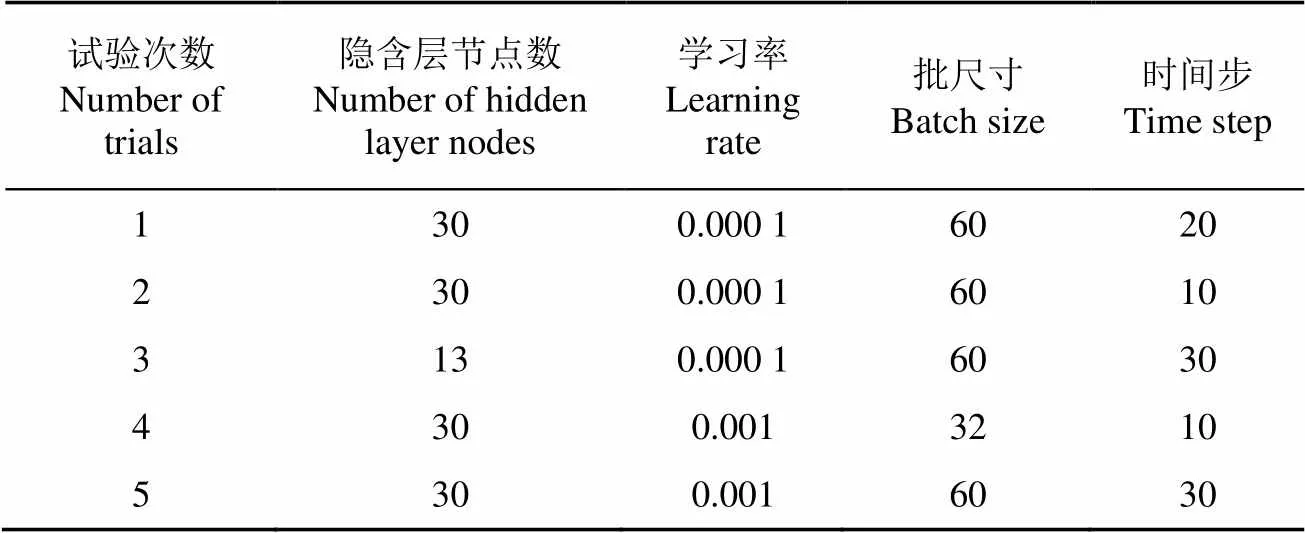
表4 PCA-LSTM算法的参数对比

图4中右列的5个图表示LSTM神经网络的预测值和实际值的变化趋势，从图中可以看出，样本集合1、3和5得到的模型精度较高且拟合性能好，样本集2和4误差波动较大，且比较分散。但是从第二列的5组图中可以看出，不同样本最后的预测结果总体趋势与实际值较吻合。

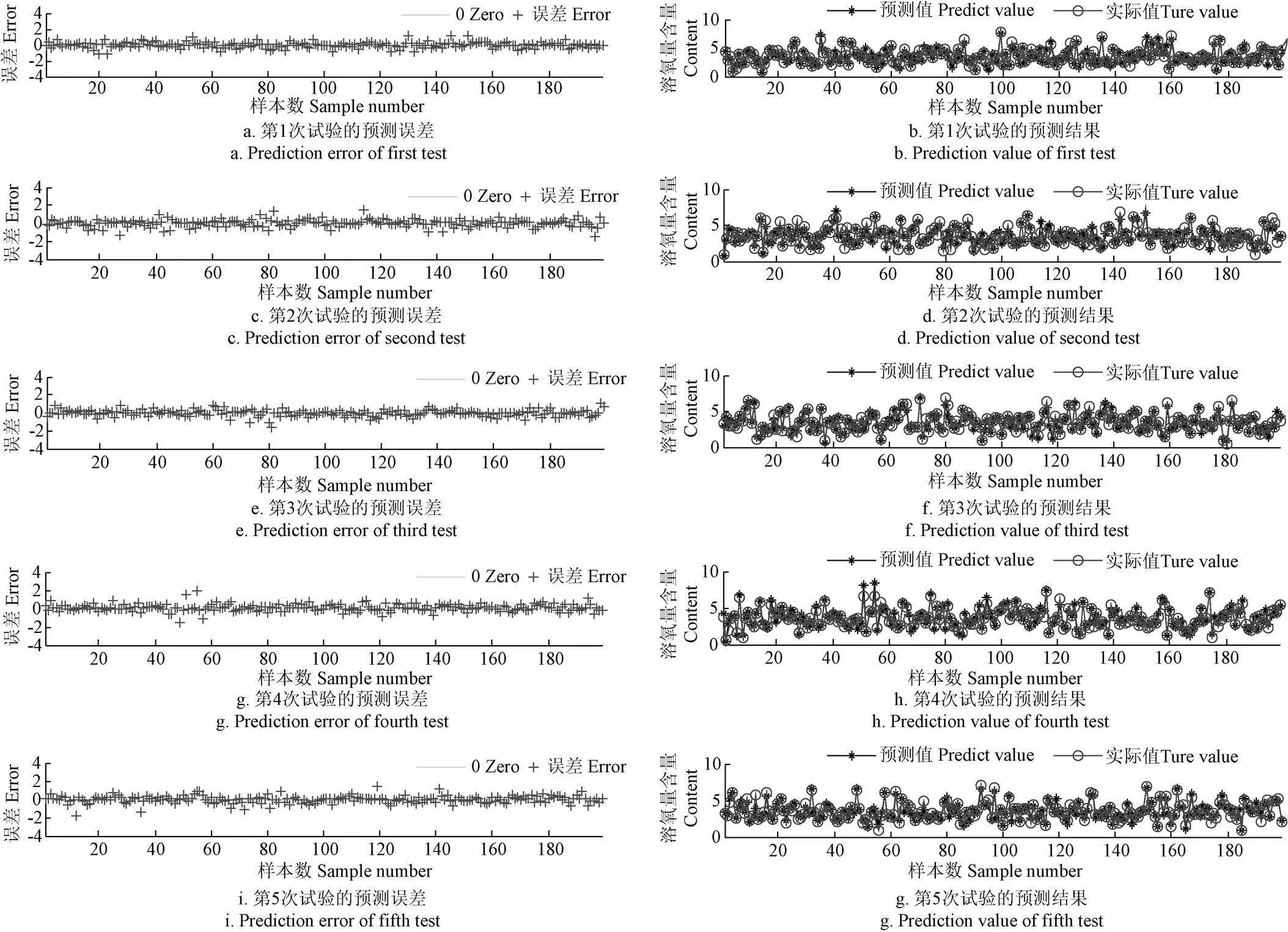
图4 PCA-LSTM模型的误差曲线和预测趋势

为了更加直观比较PCA-LSTM神经网络预测模型的误差值，表5为5次试验后得到的LSTM模型的平均相对误差、平均绝对百分误差和均方根误差的值。从表中也可以看出，相对于其他的样本集，样本1最终取得的预测性能最好，MAE、MAPE和RMSE分别达到了0.252 9、0.081 4和0.118 6。此外，PCA-LSTM模型的整体预测精度较为理想，MAE、MAPE和RMSE（保留3位有效数字）分别达到了0.274、0.089和0.147，说明了基于PCA-LSTM神经网络的水产养殖溶解氧预测模型具有较为理想的泛化性能，可以很好地拟合养殖生态环境因子与水质溶解氧之间复杂的非线性关系。

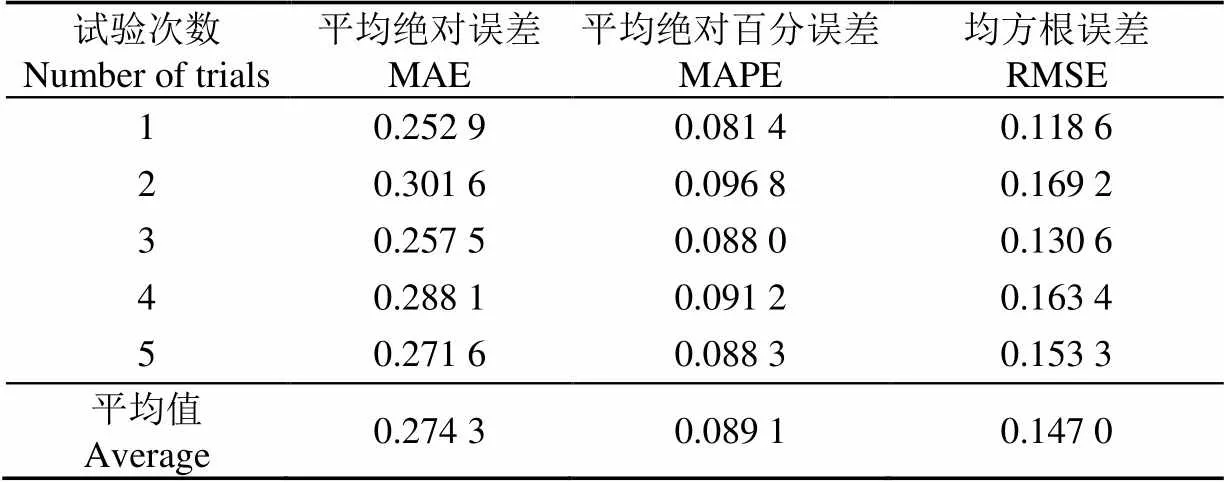
表5 PCA-LSTM预测模型的精度分析

3.2.2 模型对比

为了进一步验证PCA-LSTM神经网络的预测效果，我们采用不同的预测模型进行对比，分别为单一的LSTM模型、PCA-BP模型、PCA-PSOBP模型、PCA-ELM模型和PCA-LSSVM模型，均以相同的样本集进行5折交叉验证。图5表示PCA-LSSVM、PCA-PSO-BP、PCA-BP、PCA-ELM、单一的LSTM和PCA-LSTM的预测误差曲线。可以直观地看出，PCA-LSSVM、LSTM以及PCA-LSTM的预测值和实际值的误差较小，预测效果较为理想，并且PCA-LSTM模型的误差曲线波动较小。

由表6可知，PCA-LSTM模型比单一的LSTM模型预测精度高，PCA-LSTM模型的MAE、MAPE和RMSE（保留3位有效数字）分别为0.274、0.089和 0.147，与单一的LSTM模型相比，MAE、MAPE和RMSE分别提高了8%、1.4%和14.1%，可以看出利用PCA实现了原始数据的降维处理，消除了变量之间的冗余性和相关性，提升了LSTM模型的预测精度和稳定性。除此之外，与其他4种浅层模型相比，PCA-LSTM模型明显优于PCA-BP、PCA-PSOBP和PCA-ELM，略高于PCA-LSSVM模型。结果表明提出的PCA-LSTM模型的预测精度高、泛化能力强，能够准确掌握水产养殖溶解氧含量未来2 h的变化，达到了比较理想的预测效果，可以为水质预警和水质调控提供决策依据。

图5 各模型预测误差曲线

表6 各模型预测结果精度分析

4 结 论

本文提出并构建了基于PCA-LSTM神经网络的水产养殖溶解氧预测模型。主要结论如下：

1）采用PCA筛选出溶解氧的关键影响因子，实现了模型输入的降维，消除了变量之间的冗余性和相关性，有利于提升LSTM预测精度和稳定性；

2）本文提出的PCA-LSTM模型能够准确的预测未来2 h溶解氧含量，预测精度和稳定性较高，能够很好地拟合水产养殖溶解氧与其他生态环境因子之间的非线性关系；

3）本文提出的PCA-LSTM模型与BP神经网络等其他模型相比，模型评价指标平均绝对误差、均方根误差和平均绝对误差分别为0.274、0.089和0.147，均优于传统的预测方法，解决了传统预测方法预测精度低、鲁棒性差等问题。

本文溶解氧预测模型具有良好的预测性能和泛化能力，可以为预防水体恶化、水产疾病爆发、水质的智能调控与管理方面具有重要的指导意义。

[1] 刘双印. 基于计算智能的水产养殖水质预测预警方法研究[D]. 北京：中国农业大学，2014.

Liu Shuangyin. Prediction And Early-Warning of Water Quality in Aquaculture Based on Computational Intelligence[D]. Beijing: China Agricultural University, 2014. (in Chinese with English abstract)

[2] 徐龙琴，刘双印，张垒，等. 基于DBN-LSSVR的南美白对虾养殖溶解氧预测[J]. 仲恺农业工程学院学报，2017(4)：1－7.

Xu Longqin, Liu Shuangyin, Zhang Lei, et al. Prediction of dissolved oxygen in Litopenaeus vannamei culture based on deep belief network and least squares support vector regression[J]. Journal of Zhongkai University of Agriculture and Engineering, 2017(4): 1－7. (in Chinese with English abstract)

[3] Liang Jin, Luo Fei, Xu Yuge. Dissolved oxygen concentration prediction control through multiobjective evolutionary RBF neural network[C]// Decision and Control, 2009: 1878－1883.

[4] 陈彦，殷建军，项祖丰，等. 基于时间序列模型的海洋溶解氧分析与预测[J]. 轻工机械，2012(3)：83－87.

Chen Yan, Yin Jianjun, Xiang Zufeng, et al. Marine dissolved oxygen analysis and prediction based on the time series model[J]. Light Industry Machinery, 2012(3): 83－87. (in Chinese with English abstract)

[5] 马晓涛，温继文，陈英义. 基于ARIMA和RBF神经网络模型的溶解氧预测分析[J]. 江苏农业科学，2015(5)：413－415.

[6] 徐敏，曾光明，谢更新，等. 混沌理论在河流溶解氧预测中的应用初探[J]. 环境科学学报，2003(6)：776－780.

Xu Min, Zeng Guangming, Xie Gengxin, et al. Prelimiary research on the application of chaos theroy to dissoved oxygen prediction[J]. Acta Scientiae Circumsitantiae. 2003(6): 776－780. (in Chinese with English abstract)

[7] 朱成云，刘星桥，李慧，等. 工厂化水产养殖溶解氧预测模型优化[J]. 农业机械学报，2016(1)：273－278.

Zhu Chengyun, Liu Xingqiao, Li Hui, et al. Optimization of prediction model of dissolved oxygen in industrial aquaculture[J]. Transaction of the Chinese Society for Agricultural Machinery, 2016(1): 273－278. (in Chinese with English abstract)

[8] 刘双印，徐龙琴，李道亮，等. 基于蚁群优化最小二乘支持向量回归机的河蟹养殖溶解氧预测模型[J]. 农业工程学报，2012，28(23)：167－175.

Liu Shuangyin, Xu Longqin, Li Daoliang, et al.Dissolved oxygen prediction model of eriocher sinensis culture based on least squares support vector regression optimized by ant conlony algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(23): 167－175. (in Chinese with English abstract)

[9] 宦娟，刘星桥. 基于K-means聚类和ELM神经网络的养殖水质溶解氧预测[J]. 农业工程学报，2016，32(17)：174－181.

Huan Juan, Liu Xingqiao. Dissolved oxygen prediction in water based on K-means clustering and ELM neural network for aquaculture[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(17): 174－181. (in Chinese with English abstract)

[10] Zhao Z, Chen W, Wu X, et al. Lstm network: A deep learning approach for short-term traffic forecast[J]. Iet Intelligent Transport Systems, 2017, 11(2): 68－75.

[11] Kuremoto T, Kimura S, Kobayashi K, et al. Time series forecasting using a deep belief network with restricted boltzmann machines[J]. Neurocomputing, 2014, 137(Supp.1): 47－56.

[12] Benuwa B B, Yong Z Z, Ghansah B, et al. A review of deep machine learning[J]. International Journal of Engineering Research in Africa, 2016, 24: 124－136.

[13] LeCun Y, Bengio Y, Hinton G. Deep learning[J]. Nature, 2015, 521(7553): 436－444.

[14] Bengio Y. Learning deep architectures for AI[J]. Foundations and Trends in Machine Learning, 2009, 2(1): 1－56.

[15] Hochreiter S, Schmidhuber J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735－1780.

[16] 陈卓，孙龙祥. 基于深度学习LSTM网络的短期电力负荷预测方法[J]. 电子技术，2018(1)：39－41.

Chen Zhuo, Sun Longxiang. Short-term electrical load forecasting based on deep learnig LSTM networks[J]. Electronics Design & Application, 2018(1): 39－41. (in Chinese with English abstract)

[17] 于家斌，尚方方，王小艺，等. 基于GF-LSTM网络的蓝藻水华预测方法[J]. 计算机应用，2018：1－6.

Yu Jiabin, Shang Fangfang, Wang Xiaoyi, et al. Cyanobacterial bloom forecast method based on GF-LSTM network[J]. Journal of Computer Applications, 2018: 1－6. (in Chinese with English abstract)

[18] 王鑫，吴际，刘超，等. 基于Lstm循环神经网络的故障时间序列预测[J]. 北京航空航天大学学报，2018，44(4)：772－784.

Wang Xin, Wu Ji, Liu Chao, et al. Exploring LSTM based recurrent neural network for failures time series prediction[J]. Journal of Beijing Unversity of Aeronautics and Astronautics, 2018, 44(4): 772－784. (in Chinese with English abstract)

[19] 吴松涛，侯风华，戴锋. 非线性数据标准化处理过程中的线性近似法[J]. 信息工程大学学报，2007，8(2)：250－253.

Wu Songtao, Hou Fenghua, Dai Feng.Linear approxmiating method in the transacting process of nonlinear standardization of data[J]. Journal of Information Engineering University, 2007, 8(2): 250－253. (in Chinese with English abstract)

[20] 徐龙琴，刘双印. 基于APSO-WLSSVR的水质预测模型[J]. 山东大学学报：工学版，2012，42(5)：80－86.

Xu Longqin, Liu Shuangyin. Water quality prediction model based on APSO-WLSSVR[J].Journal of Shandong University: Engineering Science, 2012, 42(5): 80－86. (in Chinese with English abstract)

[21] Wold S, Esbensen K, Geladi P. Principal component analysis[J]. Chemometrics And Intelligent Laboratory Systems, 1987, 2(1/2/3): 37－52.

[22] Jian Z, Cencen X, Ziang Z, et al. Electric load forecasting in smart grids using long-short-term-memory based recurrent neural network[C]// Information Sciences and Systems. IEEE, 2017.

[23] Fujita T, Bai W, Quan C. Long short-term memory networks for automatic generation of conversations[C]// Software Engineering, Artificial Intelligence, Networking And Parallel/Distributed Computing, 2017: 483－487.

[24] 汤宝平，刘文艺，蒋永华. 基于交叉验证法优化参数的Morlet小波消噪方法[J]. 重庆大学学报，2010，33(1)：1－6.

Tang Baoping, Liu Wenyi, Jiang Yonghua. Parameter optimized Morlet wavelet de-noising method based on cross validation method[J]. Journal of Chongqing University, 2010, 33(1): 1－6. (in Chinese with English abstract)

[25] Hirose Y, Yamashita K, Hijiya S. Back-propagation algorithm

which varies the number of hidden units[J]. Neural Networks, 1991, 4(1): 61－66.

[26] 陈啸，王红英，孔丹丹，等. 基于粒子群参数优化和BP神经网络的颗粒饲料质量预测模型[J]. 农业工程学报，2016，32(14)：306－314.

Chen Xiao, Wang Hongying, Kong Dandan, et al. Quality prediction model of pellet feed basing on BP network using PSO parameters optimization method[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(14): 306－314. (in Chinese with English abstract)

[27] Huang G, Zhu Q, Siew C. Extreme learning machine: theory and applications[J]. Neurocomputing, 2006, 70(1/2/3): 489－501.

[28] Huang G B, Zhu Q Y, Siew C K. Extreme learning machine: a new learning scheme of feedforward neural networks[J]. Neural Network: IEEE, 2004: 985－990

[29] Huang G, Zhou H, Ding X, et al. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems Man and Cybernetics Part B-Cybernetics, 2012, 42(2): 513－529.

[30] Zhang Y, Liu Y. Traffic forecasting using least squares support vector machines[J]. Transportmetrica, 2009, 5(3): 193－213.

[31] Suykens J, Vandewalle J. Least squares support vector machine classifiers[J]. Neural Processing Letters, 1999, 9(3): 293－300.

Principal component analysis and long short-term memory neural network for predicting dissolved oxygen in water for aquaculture

Chen Yingyi1,2, Cheng Qianqian1,3, Fang Xiaomin1,3, Yu Huihui1,3, Li Daoliang1,2

(1.,,100083,; 2.,,100083,; 3.,100083,)

China has the largest aquaculture industry, accounting for almost 70% of the aquaculture production in the world. The dissolved oxygen in aquaculture directly affects the quality and safety of aquatic products. The dissolved oxygen is susceptible to many factors such as temperature, wind speed, wind direction, etc. So it is significant to understand timely and accurately the change of the dissolved oxygen content which can prevent water quality deterioration, disease outbreaks and optimize aquaculture management. The traditional methods in dissolved oxygen prediction have problems such as low prediction accuracy and poor robustness, with shortcomings like limited ability to express complex functions under limited amount of sample data as well as poor generalization ability for complicated problems. In order to improve the prediction accuracy of the dissolved oxygen in aquaculture, a hybrid model based on principal component analysis (PCA) and long short-term memory (LSTM) neural network was proposed to forecast the dissolved oxygen content in aquaculture. First, the key impact factors of dissolved oxygen in aquaculture were extracted by PCA, which can eliminate the correlations of original variable and reduce the input dimension. Therefore, the key impact factors selected were water temperature, solar radiation, wind speed, wind direction, soil temperature and soil moisture, respectively. Then, a LSTM network model was built based on Tensorflow deep learning framework to construct the nonlinear prediction model between the dissolved oxygen and these key impact factors. Finally, based on the presented prediction model of PCA-LSTM, the dissolved oxygen content was predicted for an experimental pond during July 8th, 2017 to August 8th, 2017 in the Research Institute of Freshwater Aquaculture, Zhejiang province. In the model accuracy analysis process, a 5-fold cross validation method was used to evaluate the approximation accuracy. The experimental results showed that the proposed prediction model of PCA-LSTM had better prediction performance than BP neural network (BPNN), particle swarm optimization BP neural network (PSO-BP), extreme learning machine (ELM) and least squares support vector machine (LSSVM). In the case of the same data set, the MAE, MAPE and RMSE of the PCA-LSTM were 0.274, 0.089 and 0.147, respectively; the MAE, MAPE and RMSE of LSTM were 0.354, 0.103 and 0.288, respectively; the MAE, MAPE and RMSE of PCA-LSSVM were 0.338, 0.100 and 0.297, respectively; the relative MAE, MAPE and RMSE of PCA-ELM were 0.419, 0.130 and 0.343, respectively; the relative MAE, MAPE and RMSE of PCA-PSO-BP were 0.377, 0.133 and 0.280, respectively; and the relative MAE, MAPE and RMSE of PCA-BP were 0.414, 0.141 and 0.335, respectively. It was clear that the presented prediction model was more accurate than BP algorithm, PSO-BP algorithm and ELM algorithm, slightly higher than LSSVM algorithm. The dissolved oxygen prediction model based on PCA-LSTM network exhibited best prediction accuracy and generalization performance when compared with other traditional forecasting models. Therefore, the presented model based on PCA-LSTM network can meet the actual demand of accurate forecasting of dissolved oxygen and provide a reference for water quality control in aquaculture. As well as it also can help farmers make decisions and reduce farming risks.

aquaculture; dissolved oxygen prediction; principal component analysis; long short-term memory; recurrent neural network

10.11975/j.issn.1002-6819.2018.17.024

TP391

A

1002-6819(2018)-17-0183-09

2018-05-23

2018-08-04

山东省重点研究发展计划“设施蔬菜环境准确监测与控制技术研究与示范（NO. 2017CXGC0201）”，北京市科技计划“淡水鱼大规模健康养殖智能控制技术装备研究与示范”（NO. Z171100001517016）

陈英义，副教授，博士生导师，主要研究方向为农业模型和信息处理技术。Email：chenyingyi@cau.edu.cn

陈英义，程倩倩，方晓敏，于辉辉，李道亮. 主成分分析和长短时记忆神经网络预测水产养殖水体溶解氧[J]. 农业工程学报，2018，34(17)：183－191. doi：10.11975/j.issn.1002-6819.2018.17.024 http://www.tcsae.org

Chen Yingyi, Cheng Qianqian, Fang Xiaomin, Yu Huihui, Li Daoliang. Principal component analysis and long short-term memory neural network for predicting dissolved oxygen in water for aquaculture[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(17): 183－191. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2018.17.024 http://www.tcsae.org