基于基尼系数法的全国十大水资源一级区水资源与经济社会要素时空匹配分析

杜军凯，李晓星，贾仰文，仇亚琴，张海涛，陈 静

(1.中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室，北京 100038；2.中国环境科学研究院，北京 100012)

1 概 述

水资源是一种有限而脆弱的基础性资源，具有经济、社会和生态的多维属性。众所周知，我国水资源总量丰富，多年平均水资源量2.8×1012m3，但人均占有量仅为世界平均水平1/4，且随着经济社会发展，“水多、水少、水脏、水浑”等水问题愈加突出。作为一种基础性资源，水的空间分布不均及与生产、生活水平的不匹配是制约经济社会发展的重要因素。坚持空间均衡，坚持“四水四定”——以水定城、以水定地、以水定人、以水定产是破解水资源短缺难题的必然选择[1]。与其他资源相比，水资源具有独特的流域自然属性。因此，分析研究水问题必须从水循环的基本规律出发，以流域为单元[2]，超脱就水论水的藩篱，协调好水与经济社会间的关系。如何有效地定量描述水与地、水与城、水与人、水与产等经济社会要素的关系，是分析“四水四定”的关键。

据文献调研，基尼系数法具有定量地、科学地描述不同要素的匹配程度的优势，在水资源与其他经济社会要素匹配格局定量化研究方面受到众多学者[3-6]的青睐。尽管已有研究均取得了较好的研究成果，但总的来说仍存在以下问题：①对水资源格局的分析多以行政区域为研究单元，缺乏建立在水循环基础上的流域角度研究。②研究多从空间维度入手，缺乏在时间维度上对水资源格局变化规律的揭示。③当前研究关于水资源与单一要素的匹配程度的描述较多，但具体到单元内部，“四水四定”的首要因素是什么？换言之，基于区域水资源禀赋现状条件，水资源-土地资源、水资源-人口、水资源-产值三者孰为制约经济社会发展的最强水资源约束，在此方面开展的研究较少。

2 研究思路与技术方法

2.1 研究思路

针对以上问题，本次研究依托《中国水资源公报(2004-2013)》系列数据，以流域统筹的视角来研究全国水资源的时空匹配格局，以全国10个水资源一级区为研究对象，以水资源二级区为基本计算单元，运用基尼系数法计算分析各水资源一级区的水资源与土地资源、水资源与人口、水资源与产值的匹配程度并分析各要素的时间变化趋势。研究目的如下：①在空间维度上，从流域角度分析水资源对经济社会发展的约束作用；②在时间维度上，分析各类水资源约束的变化趋势；③识别出各水资源一级区关键的制约因素。研究技术路线见图1。

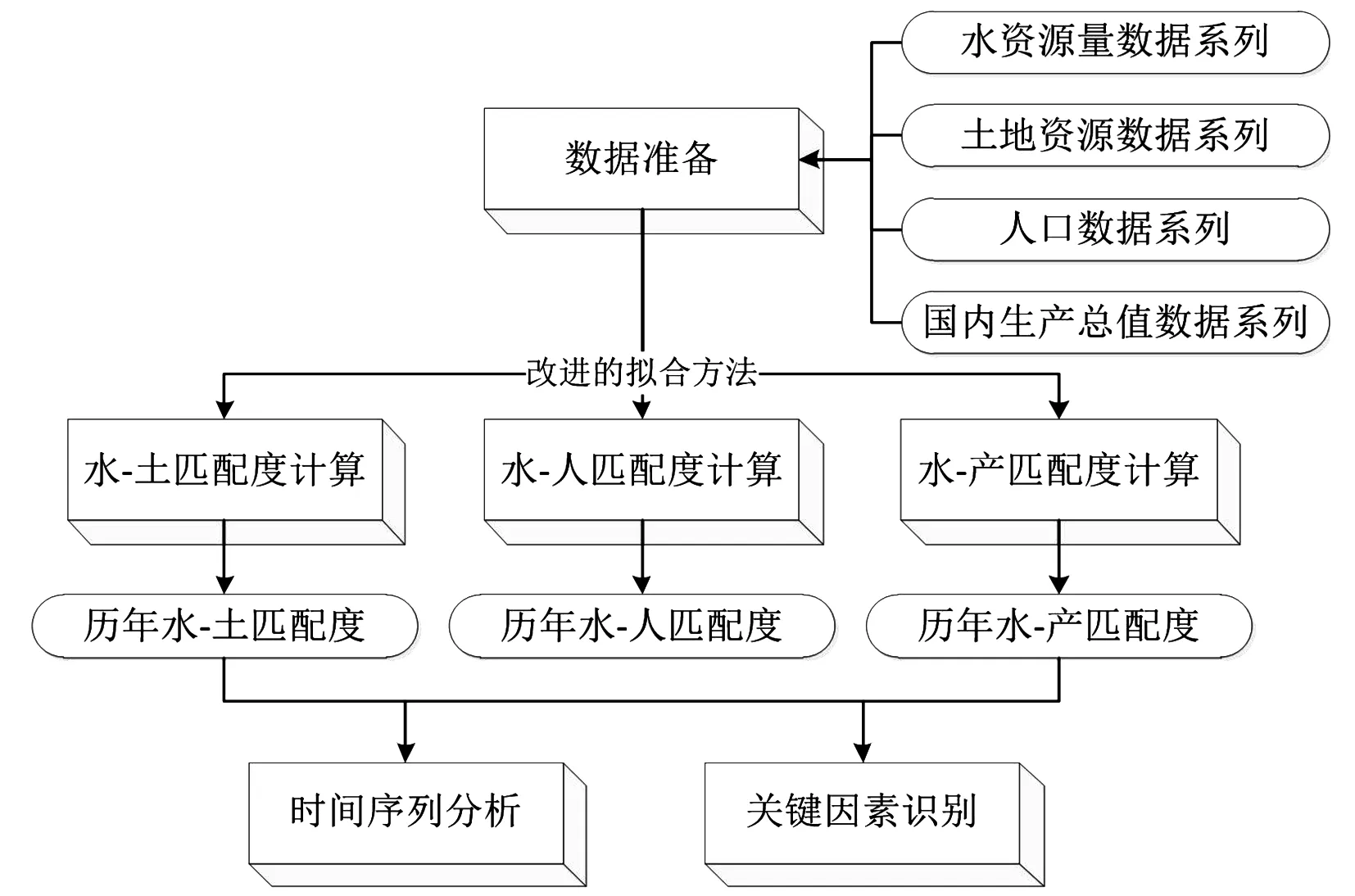
图1 研究技术路线图

2.2 基尼系数法

作为一个经济学概念，基尼系数(Gini Coefficient)最早由意大利籍学者基尼(Gini)基于洛伦茨曲线推导而出。美国经济学家Paul R. Krugman根据资源的空间分布特点，提出了用于研究区域空间维度上资源匹配的基尼系数求解模型[7]，见图2。

图2 基尼曲线示意图

图2中，横坐标为要素1的累积比例X，取值范围为[0,1]；纵坐标为要素2的累积比例Y，取值范围为[0,1]；理想分布线为图1中斜率为1的直线，记为Y=f1(x)；要素1与要素2的双累积线为图1中的Y=f2(x)；要素1与要素2的基尼曲线为图1中的Y=f3(x)。理想分布线表示在理想情况下，要素1与要素2在空间上呈绝对均匀的分布；双累积线表示实际情况下，要素1与要素2在空间上的分布情况；基尼曲线为双累积线的拟合曲线。基尼系数在数值上等于基尼曲线Y=f3(x)与理想分布线Y=f1(x)所围成的阴影部分A面积的2倍，表征要素1和要素2实际分布与理想情况下的差异。

如前所述，基尼系数在数值上等于基尼曲线与理想线所围成的阴影部分A面积的2倍，计算方法见式(1)：

(1)

本文沿用文献[8-9]对基尼系数的阈值划分：G在0～0.2区间为高度匹配；0.2～0.3区间表示相对匹配；0.3～0.4区间为比较匹配； 0.4～0.5区间为不匹配；超过0.5 为极不匹配。

2.3 趋势分析方法

2.3.1 线性趋势检验

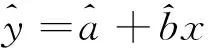
R检验过程见式(2)、式(3)

|R|>Ra

(3)

对给定的检验水平a，对比R与相关系数临界值Ra，如果满足式(3)，则认为此水平下，回归效果是显著的。

2.3.2Mann-Kendall趋势分析法

Mann-Kendall趋势检验法是一种典型的非参数检验方法。该方法构造一个标准正态分布统计量Z，对给定的检验水平a，如果满足式(4)，则认为此水平下，系列存在增大(Z>0)或减小(Z<0)的趋势，反之则认为系列无明显变化趋势。方法原理见文献[11]。

|Z|≥Z1-a/2

(4)

2.3.3 基尼曲线的正交最小二乘拟合

已有研究在研究水资源与相关资源的匹配问题时多使用最小二乘法进行基尼曲线的拟合。最小二乘曲线拟合法的使用前提是自变量本身不存在误差[12]，鲁铁定等[13]运用间接平差原理证明了在自变量误差较大时，正交最小二乘法的拟合精度显著高于普通最小二乘法。

而无论是模型计算或统计生成的水资源量成果均存在不同程度的误差。为提高计算精度，本研究选用正交多项式最小二乘法进行基尼曲线的拟合，正交多项式拟合原理介绍如下：

m次正交多项式最小二乘法拟合方程见式(5)：

p(x)=b0B0(x)+b1B1(x)+…+bmBm(x)

(5)

其中，bj(j=0,1,2,…,m)为m次正交多项式的拟合系数，构造给定的n个点上正交的m次多项式函数系Bi(x)(i=0,1,2,…,m)为基函数，见式(6)：

基函数Bj(x)(j=0,1,2,…,m)计算见式(7)：

基函数Bj(x)由系数αj和βj决定，αj和βj确定方法见式(8)：

3 实例分析

本研究的基础数据来自于《中国水资源公报》(2004-2013)。水资源公报统计报表的上报单元为水资源二级区嵌套地市，统计要素包括社会经济数据、水资源量数据和水资源开发利用数据等，为保障准确性，各报表均经过省级和全国的两重复核，相关介绍见《水资源公报编制规程》(GB/T 23598-2009)。

本研究以全国10个水资源一级区为研究对象，以79个(不含台澎金马诸河)水资源二级区为基本计算单元(图3)，采用正交二项式最小二乘拟合方法计算水资源与各社会经济要素的基尼系数。在其基础上，本文采用线性回归和M-K趋势检验方法分析不同要素之间基尼系数的变化趋势，并对分析结果进行显著性检验。

图3 全国水资源二级分区示意图

3.1 水资源与土地/人口/产值的基尼系数

全国十大水资源一级区2004～2013各对要素的基尼系数分析结果见表1、图4。

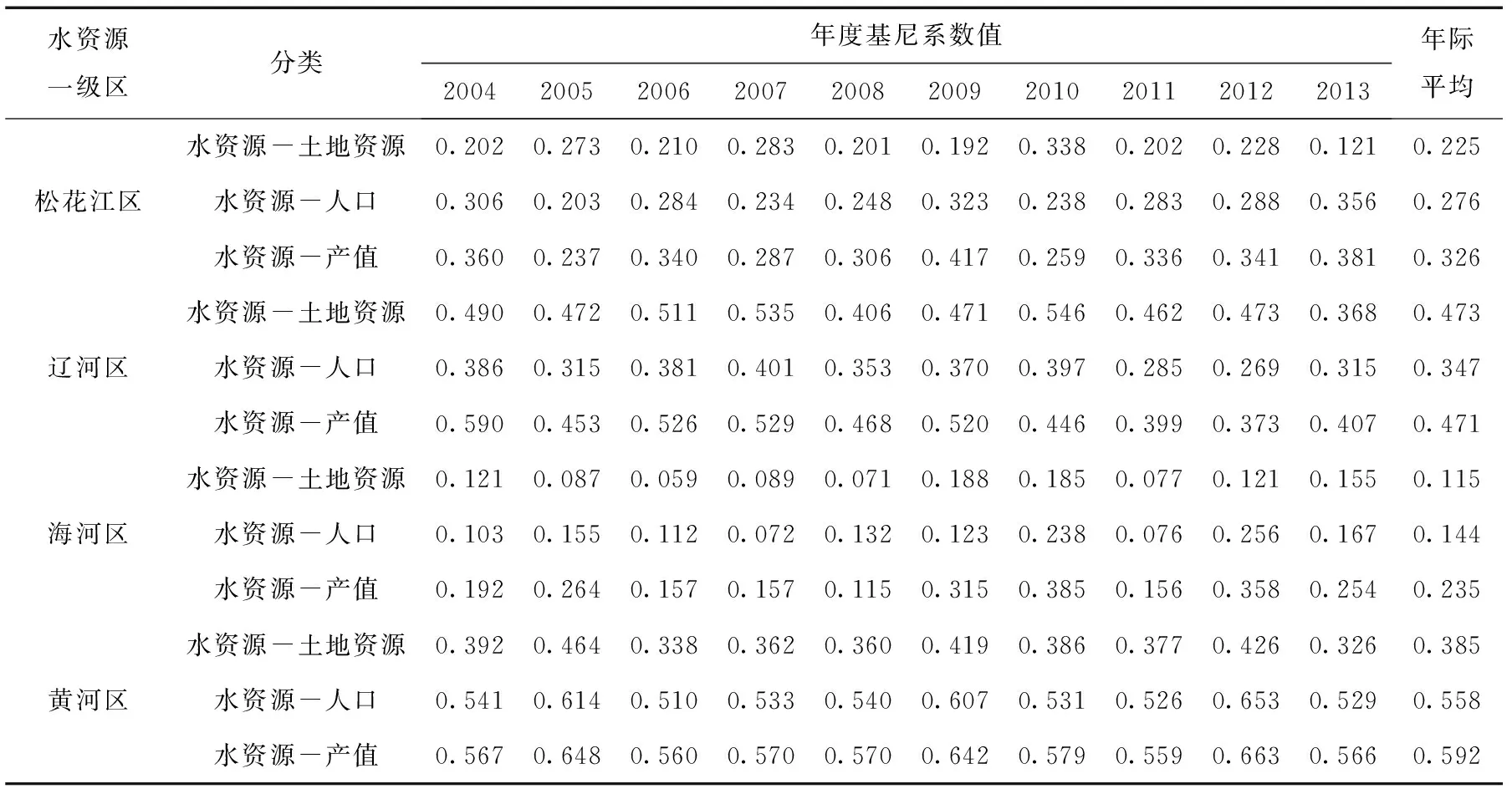
表1 全国十大水资源一级区基尼系数(2004～2013)

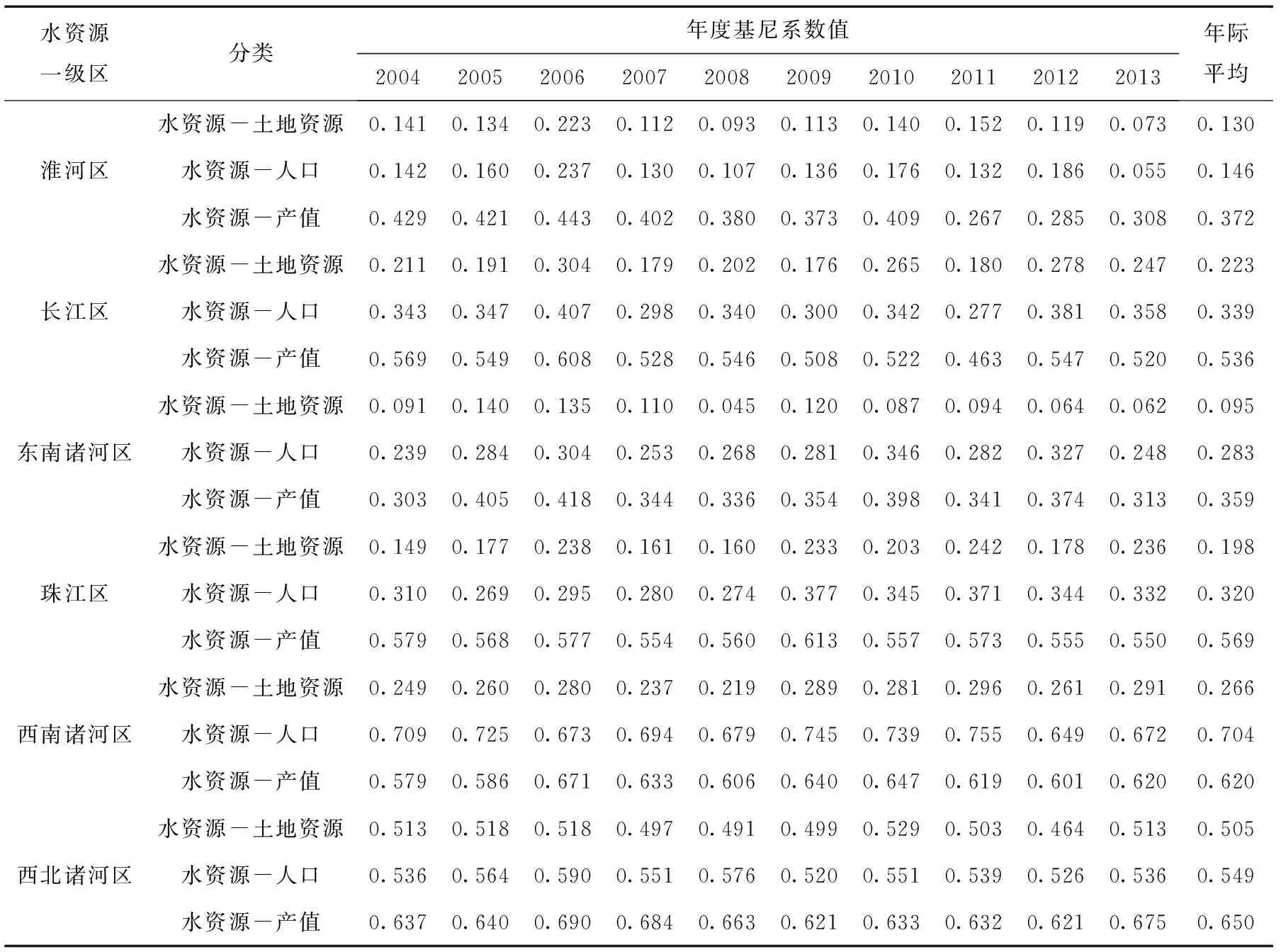
续表1

图4 全国十大水资源一级区各要素组基尼系数时空分布(2004～2013)

在空间分布上，西北诸河区、西南诸河区和黄河区各对要素的基尼系数普遍高于其他流域，反映出这些区域水资源与经济社会要素间的匹配度较差；海河区各要素组的基尼系数最低，水资源与经济社会要素的匹配度较好。

从要素类型看，水资源-产值的基尼系数普遍高于水资源-土地和水资源-人口；其中以辽河区水资源与土地资源的基尼系数最高，西南诸河区水资源与人口的基尼系数最高，其余8个一级区水资源与产值的基尼系数最高。

3.2 基尼系数变化趋势

根据本文前述趋势分析方法，全国十大水资源一级区水资源与各经济社会要素的基尼系数趋势分析分结果见表2。总体而言，两种趋势检验的结果具有较好的一致性；全国十大一级区30对要素的基尼系数的变化趋势中，呈下降趋势的有16个，呈上升趋势的有14个，下降趋势略高于上升趋势。

在空间分布上，松花江区、黄河区的水资源-土地资源的基尼系数呈下降趋势，其余2个要素组呈上升趋势；辽河区、淮河区和西北诸河区3个要素组均呈下降趋势；海河区3个要素组均呈上升趋势； 长江区、珠江区的水资源-产值的变化呈下降趋势，其余2个要素组呈上升趋势；东南诸河区水资源-人口呈上升趋势，其余2个要素组的变化呈下降趋势；西南诸河区水资源-人口的变化呈下降趋势，其余2个要素组呈上升趋势。

在要素类型上，水资源-产值和水资源-土地资源的基尼系数以下降趋势为主，全国十大一级区中下降趋势的流域个数与上升个数之比为6∶4；水资源-人口的基尼系数以上升趋势为主，下降趋势的流域个数与上升个数之比为4∶6。其中，辽河区、长江区和淮河区的水资源-产值的基尼系数下降趋势显著(显著性水平α=0.05)。

表2 全国十大水资源一级区基尼系数趋势分析

4 讨 论

文献[14]指出1995年全国水土资源匹配区域基尼系数为0.566；文献[4]的研究成果表明吉林省2010年水资源与农业产值、工业产值及人口匹配的基尼系数分别为0.574、0.632、0.503；文献[5]指出黑龙江省2002～2004年平均水资源与第二产业总产值、人口匹配基尼系数分别为0.460和0.718；文献[6]指出2012年重庆市水资源与第二产业产值与人口匹配的基尼系数分别为0.709和0.533。

据水资源区划(图3)，松花江区包含黑龙江省全部和吉林省大部，辽河区包含吉林省南部小部分区域、长江区包含重庆市全部。对比已有研究成果，从要素组间的基尼系数大小对比情况看，本文的研究成果与其一致，即研究区水资源-产值的基尼系数均大于其他要素组。另一方面，水资源一级区各要素组的基尼系数值均小于行政区的值。

造成水资源一级区基尼系数低于行政分区的原因有以下两个方面：①水资源具有流域自然属性，与行政区划相比，其在流域内的分布状态更加具有一致性，本底状态更优。②基尼系数的取值与分析单元的空间尺度有关，空间范围越大，单元内要素组间存在的差异越被均化，基尼系数则越小；空间范围越小，要素组间的差异性越能得以体现，基尼系数则越大。全国水资源一级区的空间范围普遍比省级行政区大，故本文得出水资源一级区各要素组的基尼系数普遍低于已有研究的结论是合理的。

关于趋势分析的合理性说明。需要指出的是，本文对十个水资源一级区基尼系数趋势分析的成果是初步的。一方面是资料条件限制，本研究只获取了10年的数据。如M-K分析法关于数据系列正态分布的假设要求其长度不小于10，本文的数据系列仅满足这一临界条件。另一方面因研究范围较大，难以对趋势分析成果进行直接验证。以上因素均对结果产生一定的影响。为克服以上不利因素，本文运用M-K和线性检验两种方法进行了趋势分析，二者具有较高的一致性(表2)，表明趋势分析的结果具有较高的可靠性，同时与相关研究成果的对比分析也支撑了这一点。综合来说，区域各要素组基尼系数变化趋势的分析尚需更为翔实数据以开展进一步的研究。

由于本文旨在分析水资源在要素维度上的最强约束与变化趋势，重在摸清一级流域水资源与各要素匹配程度的基本状态，故所用的水资源量数据均为天然水资源量系列，并未考虑水资源一级区内上下游单元之间调配。相对而言，基于水资源调配后的用水量和要素系列的匹配系数可认为是经济社会应对水资源压力并且主动响应后的一种优化状态，二者的系统结合将有助于动态地跟踪和分析水资源系统与经济社会系统影响机制。

5 结 论

通过对全国十大水资源一级区2004～2013年水资源-土地资源、水资源-人口以及水资源-区域生产总值各年度基尼系数的计算和趋势分析，本文结论如下：

1) 水资源分布与产值分布的不匹配是我国经济社会发展最强的水资源约束。在全国十大水资源一级区中，共有8个一级区水资源-产值的基尼系数最高，匹配程度最差。未来经济发展应更加关注产业布局与水资源分布的匹配问题：一方面须在允许范围内对现有产业结构进行适度调整以缓解缺水压力；同时，制定行业发展规划时需充分考虑这种约束作用，力争通过顶层设计层面的协调以规避风险，提高水资源对经济发展的保障能力。

2) 不同的流域应采取不同的策略应对水资源问题。由趋势分析结果可知，在十大水资源分区中，共有6个一级区的水资源-人口基尼系数存在上升趋势。因此，除考虑水资源分布与产值分布的不匹配之外，诸如海河区、黄河区、西南诸河区等流域同时需关注水资源-人口的不匹配问题；西北诸河区水资源禀赋条件较差，需更全面地统筹水资源、土地资源、人口和经济协调发展。

3) 水资源一级区各的基尼系数普遍小于省(市)的基尼系数。除考虑区域间的平衡外，解决水问题应充分认识与尊重水循环的基本规律，更加重视在流域层面对水资源的统一规划、合理配置和统筹管理，以便于最大限度发挥水资源的效率，支撑经济社会的协调、可持续发展。

4) 正如前文所述，不同时空尺度的数据系列均会影响到分析结果，因数据条件的制约，本文仅以全国水资源一级区的水资源-土地资源，水资源-人口、水资源-区域生产总值为对象开展研究。延长时间序列，将研究拓展到更为精细的分区，获取更细致的行业经济数据，更系统地揭示水资源对经济社会的瓶颈制约机制，将是下一步的重点研究内容。