基于改进PID控制的三关节机械臂运动轨迹跟踪误差研究
宁 煜
(陕西工业职业技术学院机械工程学院,陕西 咸阳 712000)
在机器人技术的发展过程中,机械臂是应用较为广泛的自动化装置,在工业制造、太空、军事及医疗领域都有其身影[1-2]。机械臂主要包括3个部分:1)机械主体;2)机械驱动系统;3)机械控制系统。其能够替代手工业劳动,可以实现自动控制、重复编程,不仅生产效率高,而且生产成本低。机械臂是机器人的一个分支,是当今社会发展的高科技设备,智能化程度较高,能够实现感知外界环境、发布指令和提供驱动动力等多种功能。在执行复杂任务时,若控制系统输出不稳定,就会导致不可预计的经济损失,因此研究机械臂稳定的控制方法,对于促进智能化发展具有重大意义。
机械臂控制系统相对复杂,必须设计出具有较强稳定性的控制器才能完成末端关节运动轨迹的精确定位[2]。大量科研人员对机械臂运动轨迹的稳定性控制展开了研究。例如:文献[3]、[4]研究了欠驱动机械臂PID控制算法,创建机械臂平面动力学模型,采用粒子群优化算法对PID控制参数进行整定,设计了改进PID控制系统,给出了控制系统流程图,通过仿真验证系统输出的稳定性,从而快速实现了机械臂运动轨迹跟踪。文献[5]、[6]研究了机械臂智能控制与PID控制算法,采用RBF 神经网络的PID控制器,通过仿真验证神经网络PID控制系统的输出精度,较好地实现了机械臂关节运动轨迹的跟踪。但是,以往研究的机械臂关节在受到外界环境因素的影响时,其输出轨迹与预期运动轨迹误差较大。为此,对三关节机械臂运动轨迹采用改进的单神经元PID控制方法。在数学软件Simulink中,对机械臂末端关节运动轨迹输出误差进行仿真验证,并与改进前的控制方法进行对比和分析,为降低机械臂关节运动轨迹误差研究提供了理论依据。
1 三关节机械臂模型
本文以三关节机械臂为研究对象,其关节简图如图1所示。
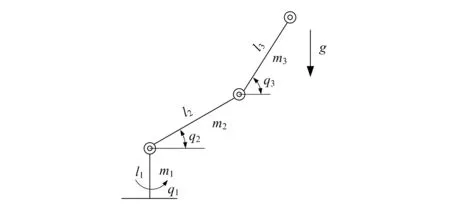
图1 三关节机械臂简图
图中:q1,q2,q3分别为关节1、关节2、关节3的角位移;m1,m2,m3分别为关节1、关节2、关节3的质量;l1,l2,l3分别为关节1、关节2、关节3的长度;g为重力加速度。
采用拉格朗日方法,可以推导出三关节机械臂动力学方程式[7]为:
H(q)q′+C(q,q′)q′+F(q′)+G(q)+τd=τ
(1)
式中:H(q)为机械臂的惯性矩阵;C(q,q′)为机械臂的离心力和哥氏力组成的矩阵;G(q)为重力矢量;F(q′)为摩擦力矩阵;τ为控制力矩阵;τd为干扰矩阵。
2 机械臂改进PID控制
2.1 PID控制
PID控制器采用比例、积分、微分计算出控制量进行控制,其控制原理如图2所示。
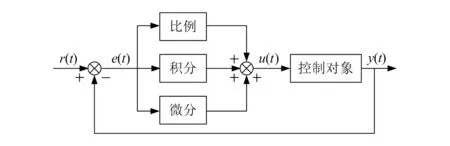
图2 PID控制原理图
理论输入值r(t)与实际输出值y(t)之间一定会有误差e(t),其方程式为:
e(t)=r(t)-y(t)
(2)
PID控制器通过对误差的比例、积分及微分的控制量,对被控对象进行在线调节,其在线控制方程式[8]为:
(3)
式中:KP为比例系数;TI为积分时间常数;TD为微分时间常数。
2.2 微分跟踪器
PID控制器采用微分跟踪器,能够输出原始信号的最佳逼近。微分跟踪器具有较强的抗外界干扰能力,无超调的跟踪原始信号,其控制方程式[9]为:
(4)
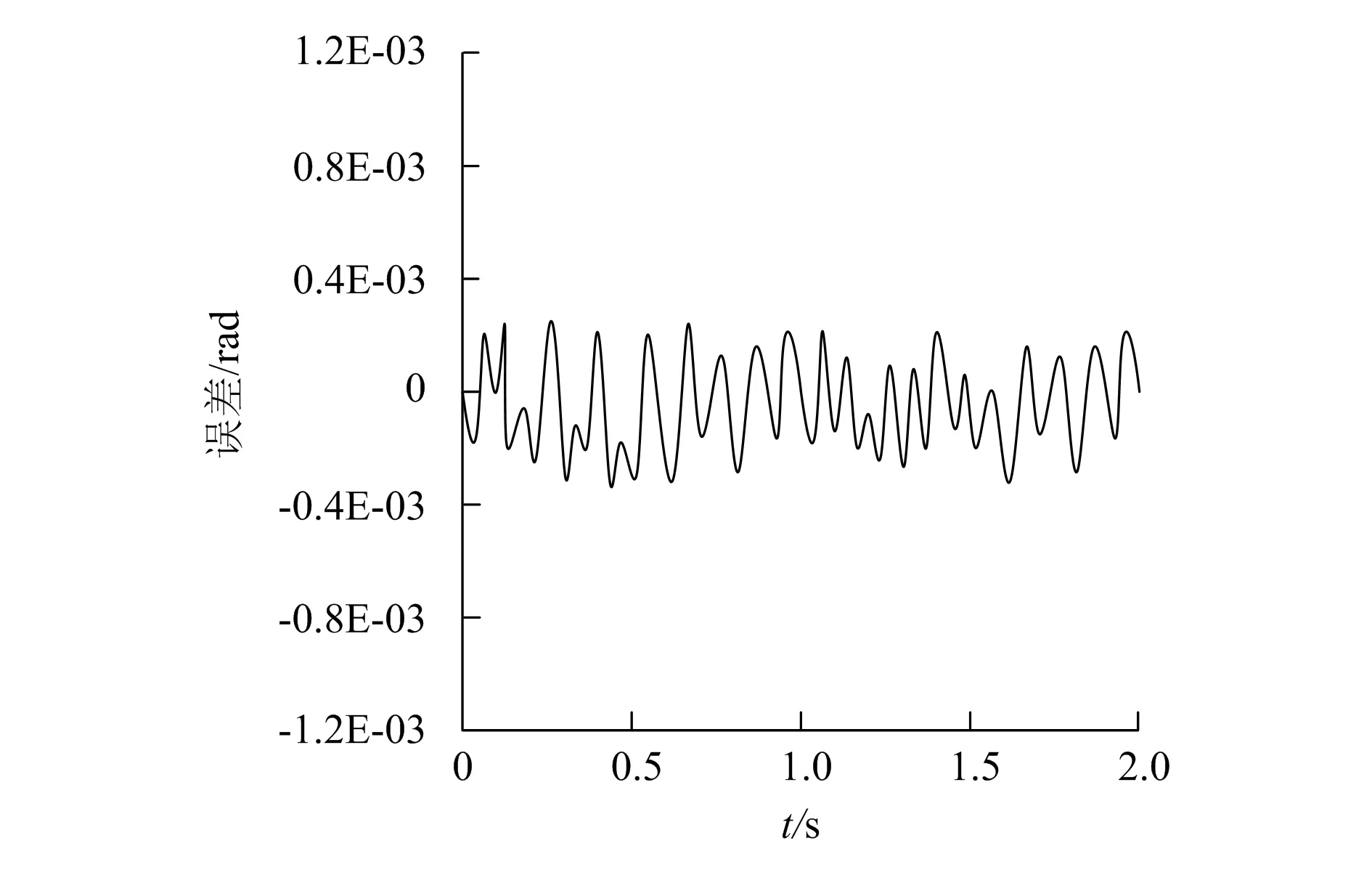
式中:v(t)为噪声位置信号;x1为跟踪信号;R>0;a0,a1,b0,b1为大于等于零的实数;m,n为大于0的奇数,且m 当a1=b1=0时,微分跟踪器跟踪控制方程式为: (5) 单神经元是神经网络的基本单位,其结构简单、计算方便且具有自适应学习能力。单神经元PID控制能够克服传统PID控制器不易在线实时整定参数的缺点,能够对参数时变、非线性、强耦合系统进行有效的控制。单神经元PID控制原理如图3所示。 图3 单神经元PID控制原理图 单神经元控制器通过修改加权系数,从而完成自适应、自组织功能。根据有监督的Hebb学习规则来修改权系数,其控制算法方程式[10]为: (6) 式中:x1(k)=e(k);x2(k)=e(k)-e(k-1);x3(k)=e(k)- 2e(k-1) +e(k-2);k为单神经元的比例系数,k>0。 学习算法方程式[10]为: (7) 式中:z(k)=e(k);ηI为积分学习速率;ηP为比例学习速率;ηD为微分学习速率。 单神经元PID控制器采用增量式控制方式,其控制算法[10]如下: Δu(k)=u(k)-u(k-1)=KP[e(k)-e(k-1)]+KIe(k)+KD[e(k)-2e(k-1)+e(k-2)] (8) 式中:KI为积分调节系数;KD为微分调节系数。 采用微分跟踪器耦合单神经元PID控制器是对传统PID控制的改进,其控制器的结构如图4所示。 图4 改进单神经元PID控制器结构 输入、输出微分信号通过微分跟踪器进行滤波,采用单神经元PID控制器对PID控制参数进行整定,从而给出控制信号。传统PID控制算法中,由于是全量输出,导致每次输出都与上一次输出有关。为了减少误差累积量,提高计算效率,对增量式PID控制器进行改进,采用微分器输出的离散微分信号,如下所示: Δu(k)=KP[e(k)-e(k-1)]+KIe(k)+KD[de(k)-de(k-1)] (9) 假设:y(k)为微分器输出位置信号,dy(k)为速度信号,v(k)为输入信号,则: de(k)=d[yd(k)-y(k)]=dyd(k)-dy(k) (10) 采用微分器输出微分信号,可以缩短采样周期,降低系统输出误差。 三关节机械臂在执行任务时,关节1的运动通过关节2传递到关节3,因此关节3运动轨迹产生的误差相对最大。采用数学软件MATLAB对机械臂关节3运动轨迹跟踪误差进行仿真,初始参数设置如下:机械臂关节期望运动轨迹为q3=cos(2πt),初始角位移为q(0)=[0 0 0]T,外界干扰波形为τ1=10sin(2πt),连杆的长度为l1=l2=l3=1.0m,连杆的质量为m1=m2=m3=1.0kg,重力加速度为g=10m/s2,仿真时间为t=4s。假设外界环境没有干扰,采用PID控制器误差仿真结果如图5所示,采用改进单神经元PID控制器误差仿真结果如图6所示。假设外界环境受到正弦波干扰,采用PID控制器误差仿真结果如图7所示,采用改进单神经元PID控制器误差仿真结果如图8所示。 对比图5、图6可知,机械臂关节3在理想环境条件下,PID控制器产生的最大误差为0.34×10-3rad,改进单神经元PID控制器所产生的最大 误差为0.22×10-3rad,二者跟踪误差大致相同。 图5 无干扰时PID控制器输出误差 图6 无干扰时改进PID控制器输出误差 图7 有干扰时PID控制器输出误差 图8 有干扰时改进PID控制器输出误差 对比图7、图8可知,机械臂关节3在受到正弦波干扰时,PID控制器产生的最大误差为0.76×10-3rad,改进单神经元PID控制器所产生的最大误差为0.22×10-3rad,二者跟踪误差相差较大。对比误差跟踪结果可知,采用改进的单神经元PID控制方法能够抵抗外界环境因素的干扰,系统输出的稳定性较好,因此可以提高机械臂末端执行器的跟踪精度。 本文针对外界环境对机械臂末端关节跟踪控制的干扰,采用了改进单神经元PID控制方法,考虑到传统PID控制方法不能抑制系统的抖动现象,将抑制外界环境干扰因素作为控制目标,在PID控制方法的基础上,增加神经网络和微分控制器,使系统输出信号更加稳定,从而降低机械臂运动轨迹跟踪误差。通过仿真实验验证可知,改进单神经元PID控制方法具有很强的鲁棒性和控制精度,有效抑制了外界波形对机械臂运动轨迹的干扰。2.3 单神经网络PID控制器

2.4 微分跟踪器耦合单神经元PID控制器

3 误差仿真及分析



4 结束语

