数学能力的改善:针对工作记忆训练的元分析*
郭丽月 严 超 邓赐平
数学能力的改善:针对工作记忆训练的元分析*
郭丽月 严 超 邓赐平
(华东师范大学 心理与认知科学学院, 上海 200062)
工作记忆训练指针对工作记忆各成分进行的训练, 以实现个体记忆与其他认知能力的提升。该领域一直都是研究者关注的热点, 越来越多的研究正在试图利用工作记忆训练改善个体的数学能力。然而回顾过往的研究, 发现研究所关注的数学能力类型、针对的被试人群、使用的方法、结论等存在较大差异, 目前尚没有系统性综述专门探讨工作记忆训练对数学能力的影响。因此, 本文首先回顾和数学能力有关的工作记忆训练方式, 然后结合元分析, 从数感、运算能力和数学推理能力三个方面, 分别回顾归纳工作记忆训练对数学能力的提升作用。具体而言, 尽管研究数量相对有限, 工作记忆训练可能有效改善数感, 其效应量为中等(Cohen’s= 0.51); 而可能无法有效改善运算和数学推理能力, 它们的效应量小(运算:Cohen’s= 0.04; 数学推理:Cohen’s= −0.06)。此外, 训练目标类型与训练效果有着密切的联系。
工作记忆训练; 数学能力; 数感; 运算; 数学推理
1 引言
工作记忆训练指对存储系统(包括语音回路(phonological loop)、视空模板(visuospatial sketchpad))或中央执行系统(包括转换(shifting process)、刷新(updating)和抑制(inhibition)成分)的训练, 通过提升个体工作记忆容量或工作记忆资源使用效率, 从而产生迁移效应(von Bastian, Langer, Jäncke, & Oberauer, 2013; 黎翠红, 何旭, 郭春彦, 2014; 刘春雷, 周仁来, 2012)。常见的训练模式主要有两大类, 一类是针对单一系统(如语音回路)进行训练, 另一类针对多种系统(如语音回路与视空模板)进行同时训练。
工作记忆在数学能力的发展中发挥重要作用, 研究显示不论是成人还是儿童, 正常发展还是发展障碍儿童, 工作记忆所有子成分的加工过程都与数学表现的优劣(比如运算)存在密切联系(Friso-van den Bos, van der Ven, Kroesbergen, & van Luit, 2013; Raghubar, Barnes, & Hecht, 2010)。鉴于此, 研究者开始逐步关注工作记忆训练对数学能力的提升或者改善效果。尽管, 过去有综述和元分析探讨了工作记忆训练对数学能力的提升效果(Peijnenborgh, Hurks, Aldenkamp, Vles, & Hendriksen, 2016; Schwaighofer, Fischer, & Bühner, 2015; 刘春雷, 周仁来, 2012), 但其或者只从数学能力的单个维度探讨, 或者一概而论。事实上数学能力是一个多维概念, 涉及数感、运算能力和数学推理能力等多个层面(Geary, 2006)。过去的研究结果存在很大的异质性, 具体来说, 不同的研究关注数学能力的不同层面(如数感、运算和数学推理), 纳入不同特征的被试群体(如不同年龄、心理发展状况)、使用不同的干预手段, 都可能会导致不同的研究结论(Alloway, 2012; Ang, Lee, Cheam, Poon, & Koh, 2015; Bergman-Nutley & Klingberg, 2014; Dahlin, 2013; Dunning, Holmes, & Gathercole, 2013; Harrison et al., 2013; Kroesbergen, Van’t Noordende, & Kolkman, 2012, 2014; Kyttälä, Kanerva, & Kroesbergen, 2015; Nelwan & Kroesbergen, 2016; Redick et al., 2013; Robert et al., 2016; Söderqvist & Nutley, 2015; Witt, 2011)。因此, 从单一维度或者笼统地探讨工作记忆训练对于数学能力的作用可能会阻碍我们对于工作记忆训练迁移效果的理解。然而, 目前尚未有综述专门针对数学能力这些不同层面的迁移效应做过系统地概括和探讨。本文试图从数感、运算和数学推理这三个层面着手, 结合元分析的研究方法, 深入探讨工作记忆训练对数学能力的提升和改善效果, 并分析影响训练效果的可能因素, 在前人工作记忆训练元分析的基础上(Melby- Lervåg & Hulme, 2013; Peijnenborgh et al., 2016; Schwaighofer et al., 2015), 我们将聚焦考察年龄、被试类型、训练目标、训练任务、控制组类型、训练强度、训练频率、每次训练时长和训练持续时间对训练效果的影响。
2 工作记忆的训练任务
在介绍工作记忆训练对不同数学能力的提升效果之前, 我们首先回顾与数学能力有关的工作记忆训练方式, 以更好理解工作记忆的训练类型及训练目标, 本文主要从工作记忆单一系统以及多系统的这两个训练模式进行总结。
2.1 单一成分训练任务
2.1.1 语音回路
分类工作记忆广度任务(Categorization Working Memory Span task, CWMS)分类工作记忆广度任务适用于9~86岁的被试群体(Borella, Carretti, & De Beni, 2008; Giofrè, Mammarella, & Cornoldi, 2013), 其训练周期一般为3个系列, 每个系列持续时间大约60分钟。在每个系列中, 被试将会完成一项任务, 这项任务包含有一系列以语音形式呈现的词语, 被试被要求记住这些词语, 待词语呈现完毕后将任务要求回忆的词语写出来(如图1所示)。三项任务的广度都为2~5个单元, 即呈现的词语在2~5个之间变化 (Borella, Carretti, Riboldi, & De Beni, 2010)。
2.1.2 视空模板
(1) 找不同(Odd One Out, OOO)
找不同任务, 适用的年龄范围为4~22岁(Alloway, Gathercole, Kirkwood, & Elliott, 2008)。任务会呈现三个图形, 其中一个形状与另外两个不同(如图2-A), 被试需要辨认出不同的图形并记住它所在的位置, 当每次所有刺激呈现完毕之后, 会呈现空白方格(如图2-B), 要求被试在上面指出那个不同图形所对应的位置。任务难度通过增减试次中刺激的呈现数量来进行调整, 同时, 被试所需记忆的图形数量也随之改变。这项任务的主要指标是广度, 即被试最多能够正确回忆多少个不同刺激所在位置。
在van der Molen, van Luit, van der Molen, Klugkist和Jongmans (2010) 的训练中, 被试每周接受3次训练, 每次6分钟, 持续5周, 训练难度从1到7单元逐步递增, 并随着被试的表现而改变。
(2) Cogmed JM
Cogmed是应用最为广泛的工作记忆训练程序(www.cogmed.com), Cogmed工作记忆训练包含3个版本, 分别为Cogmed JM 、Cogmed RM和Cogmed QM, 其中Cogmed JM(如图3所示)专门针对视空模板进行训练。在Cogmed JM中, 每天训练15~20分钟, 每周训练5天, 持续训练5周, 适用人群为4~6岁的学前儿童。训练包括7个视空间工作记忆任务, 具体为水塘任务(Pool)、动物任务(Animals)、碰碰车任务(Bumper Cars)、过山车任务(Rollercoaster)、摩天轮任务(Ferris Wheel)、旅馆任务(Hotel)、旋转任务(Twister)。以动物任务为例, 任务以转盘为背景, 在转盘上有8种动物, 这些动物以随机的顺序变亮, 要求受训儿童按呈现顺序依次点击。

图1 广度为3的CWMS任务范例(Borella et al., 2010; Carretti, Cornoldi, De Beni, & Palladino, 2004)。词语以每秒1个呈现, 听到动物词语时轻击桌面, 并记住每个系列中的某个词汇, 词语系列之间的时间间隔为2秒。所有词语系列呈现完毕后, 回忆所有要求记住的词汇。
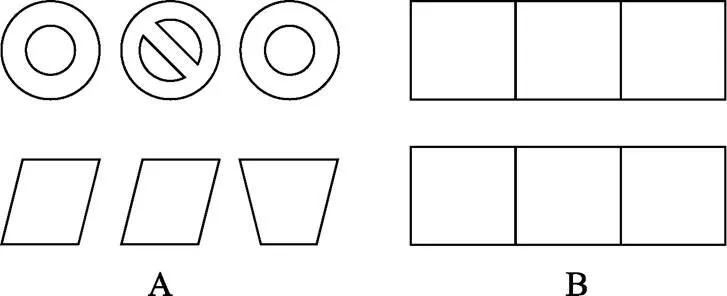
图2 广度为2的找不同任务范例 (Henry, 2001)。A)刺激; B)反应卡片。先呈现反应卡片, 之后呈现刺激, 要求指出每行中不同的图形并记住其位置, 之后在反应卡片上指出不同图形对应位置。
2.1.3 刷新
(1) N-back任务
N-back任务根据刺激呈现的形式, 可以分为视觉N-back任务和听觉N-back任务。一些研究进行一种形式的N-back任务训练, 如视觉空间位置的N-back训练(Jaeggi, Buschkuehl, Jonides, & Shah, 2011), 在训练中, 呈现6个位置, 一只青蛙随机在这6个位置出现, 要求判断每一次青蛙出现的位置与此前第n次出现时所在的位置是否一样(见图4)。也有研究使用双N-back任务, 如同时呈现视觉的位置和听觉的字母进行训练(Jaeggi, Buschkuehl, Jonides, & Perrig, 2008), 视觉的任务为在8个位置呈现方块, 要求判断每一次出现方块的位置是否与此前呈现过的第n个方块所在的位置一致, 与此同时, 听觉上呈现字母语音, 要求判断当前所听到的字母与之前听到的第n个字母是否一样(见图5)。
在研究中, N-back的指标主要包括被试所能达到的水平n, 正确率与反应时。在不同研究中, 训练强度有所不同, 一般每次的训练时间范围大概在10~45分钟, 训练次数为8~20次, 在训练中, 任务难度与被试的表现相匹配, 训练结束给予一定的奖励。
(2) 活动记忆任务(Running Memory, RM)
活动记忆任务最早由Pollack, Johnson和Knaff (1959)设计, 任务以视觉或听觉方式呈现一系列未知长度的项目串后, 要求按顺序回忆一个指定长度的项目串。比如在屏幕中呈现字母串Q、A、I、N、D、T, 之后要求回忆最后三个字母, 即NDT。任务的刺激内容包括字母、数字、位置或图片, 可通过改变项目串的长度和指定回忆的长度, 或者刺激呈现的时间长短来改变任务难度。活动记忆任务在研究中用于6~75岁的被试群体(Ang et al., 2015; Jahanshahi, Saleem, Ho, Fuller, & Dirnberger, 2008)。
活动记忆任务的指标同样为广度, 该任务训练刷新能力, 在赵鑫等人(赵鑫, 王一雪, 刘丹玮, 周仁来, 2011)的研究中, 每天训练15~20分钟, 每周3~4次, 共完成15次的训练。

图3 Cogmed JM (Pearson Inc., www.cogmed.com)
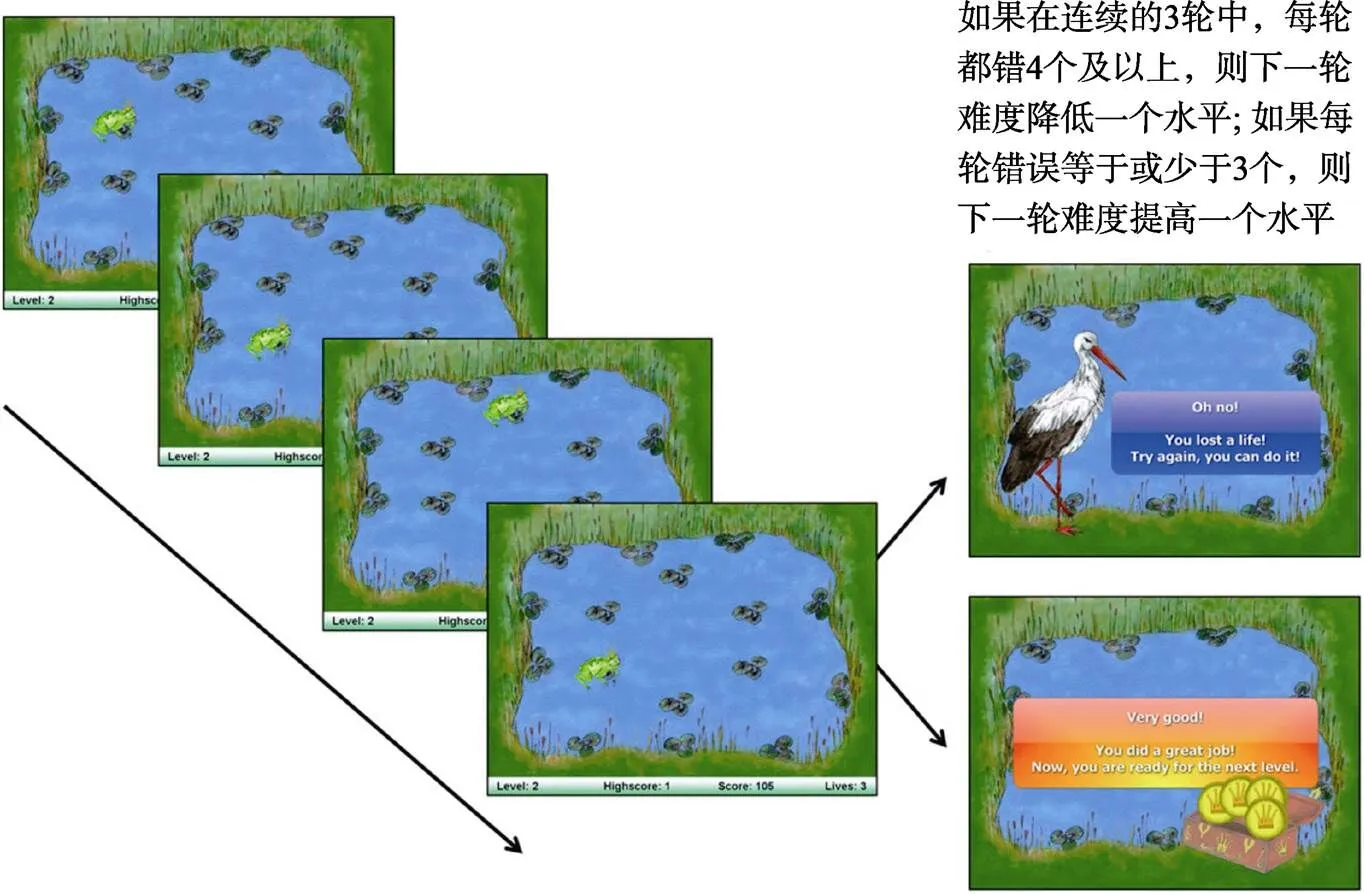
图4 空间n-back (Jaeggi et al., 2011)。青蛙在6个位置随机出现, 呈现时间500 ms, 试次之间的时间间隔2500 ms。每个回合有15+n个试次, 每个试次中要求判断每一次青蛙出现的位置与此前第n次出现时所在的位置是否一样。
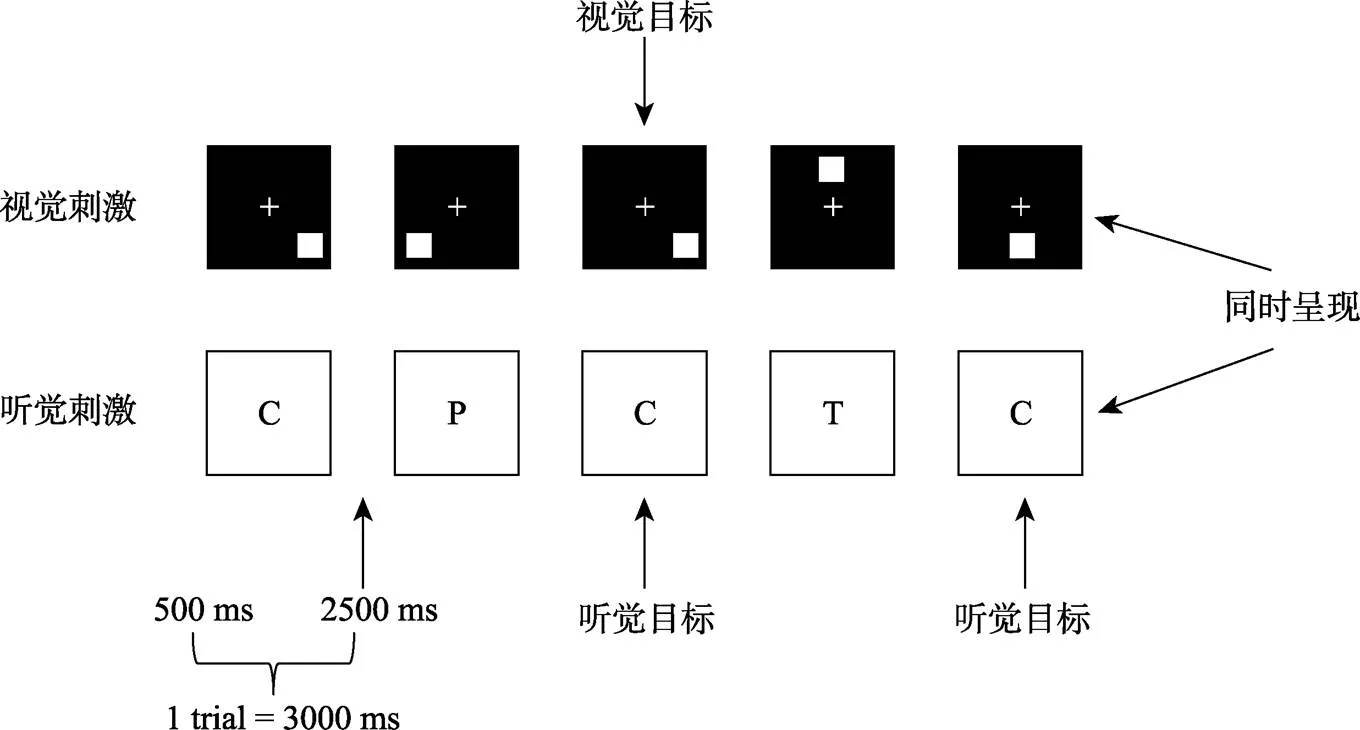
图5 双N-back范例(Jaeggi et al., 2008)。同时呈现视觉的位置和听觉的字母任务, 视觉的任务为在8个位置呈现方块, 要求判断每一次出现方块的位置是否与此前呈现过的第n个方块所在的位置一致, 一致时按“A”键, 与此同时, 听觉上呈现字母语音, 要求判断当前所听到的字母与之前听到的第n个字母是否一样, 一样时按“L”键。
2.2 多成分训练任务
2.2.1 Cogmed工作记忆训练(Cogmed Working Memory Training, CWMT)
Cogmed工作记忆训练的另外两个版本为Cogmed RM和Cogmed QM (见表1), 其中Cogmed RM版本每天训练30~45分钟, 针对7~18岁的学龄儿童和青少年设计, 包括13个言语工作记忆和视空间工作记忆任务, 这些任务分别为资料室任务(Data room)、编码者任务(Decoder)、分类者任务(Sorter)、3D立方体任务(3D cube)、行星游戏(Asteroids)、旋转数字连线任务(Rotating data link)、旋转点阵任务(Rotating dots)、太空漫步游戏(Space Whack)、输入模式任务(Input module)、视觉数字连线任务(Visual data link)、限制输入模式任务(Input module with lid)、校正者任务(Corrector)、平衡杆游戏(Stabilizer)。以视觉数字连线任务为例(见图6-A), 表盘上的红灯以随机顺序亮起, 呈现完之后要求按顺序依次点击这些变亮的灯。Cogmed QM每天训练30~45分钟, 适用于成人, 训练任务包括扭动任务(Twist)、3D网格任务(3D Grid)、校正任务(Correct)、隐藏任务(Hidden)、立方体任务(Cube)、分类任务(Sort)、弹出任务(Pop-Up)、网格任务(Grid)、数字任务(Numbers)、字母任务(Letters)、旋转任务(Rotating)、混沌任务(Chaos)、组装任务(Assembly)等13个任务。例如隐藏任务(见图6-B), 受训者在听到一系列的数字之后, 需要按顺序在表盘上点击这些数字。以上两个版本的训练强度均是每周训练5天, 持续5周。

表1 Cogmed三个版本的比较

图6 Cogmed 任务界面(Pearson Inc., www.cogmed.com)。A)视觉数字连线, 表盘上的红灯以随机的顺序变亮, 要求按顺序依次点击这些变亮的灯; B)隐藏任务, 要求在听到一系列的数字之后在表盘上按顺序点击这些数字。
2.2.2 丛林记忆(Jungle Memory, JM)
丛林记忆(http://junglememory.com)为在线干预任务(T. Alloway, 2012; T. P. Alloway, Bibile, & Lau, 2013), 训练语音回路和视空模板, 适用于7~16岁的儿童, 包括三个游戏, 游戏一针对视空模板, 如图7-A所示, 字母在矩阵中呈现, 要求记住目标刺激的位置; 游戏二针对视空模板, 如图7-B所示, 呈现两个字母, 其中一个字母旋转, 被试需要记住旋转字母配对所旋转的角度, 当一系列的字母呈现结束后, 需要按顺序将这些字母的旋转角度回忆出来; 游戏三针对语音回路, 要求解决难度逐渐增大的数学运算问题, 如图7-C所示, 左侧呈现运算问题, 右侧呈现数字键, 受训者在此输入正确答案, 等题目呈现完毕,按顺序回忆这些答案。该程序的难度有30个水平, 且训练难度随受训者的表现而改变。
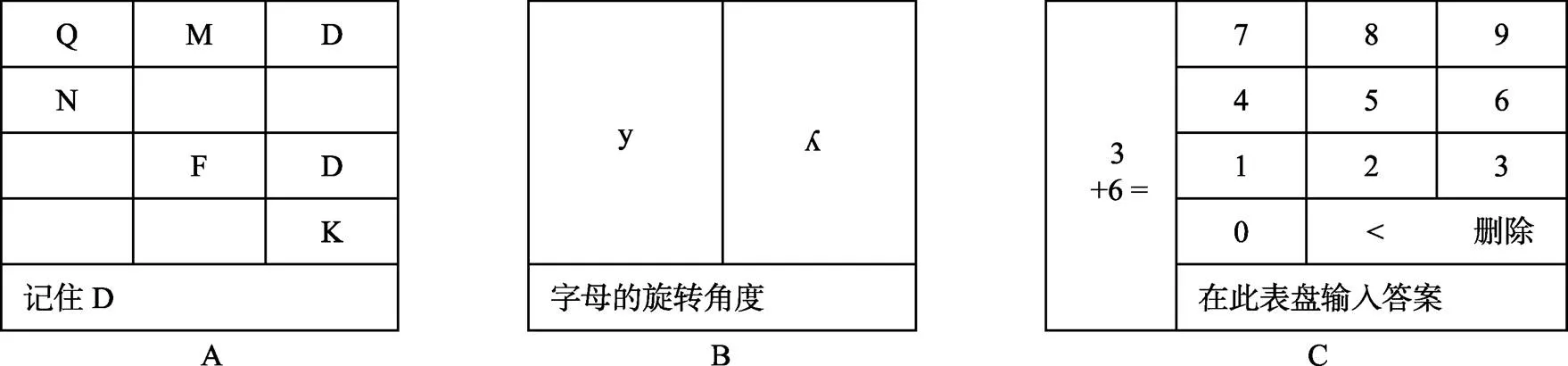
图7 丛林记忆任务(Memosyne Ltd., http://junglememory.com)。A) 矩阵任务, 在矩阵中呈现字母, 要求记住目标刺激的位置; B)字母旋转任务, 呈现两个字母, 其中一个字母被旋转, 要求记住其旋转角度, 当一系列的字母呈现结束后, 按顺序回忆这些字母的旋转角度; C)计算广度任务, 要求解决难度逐渐增大的数学运算问题。
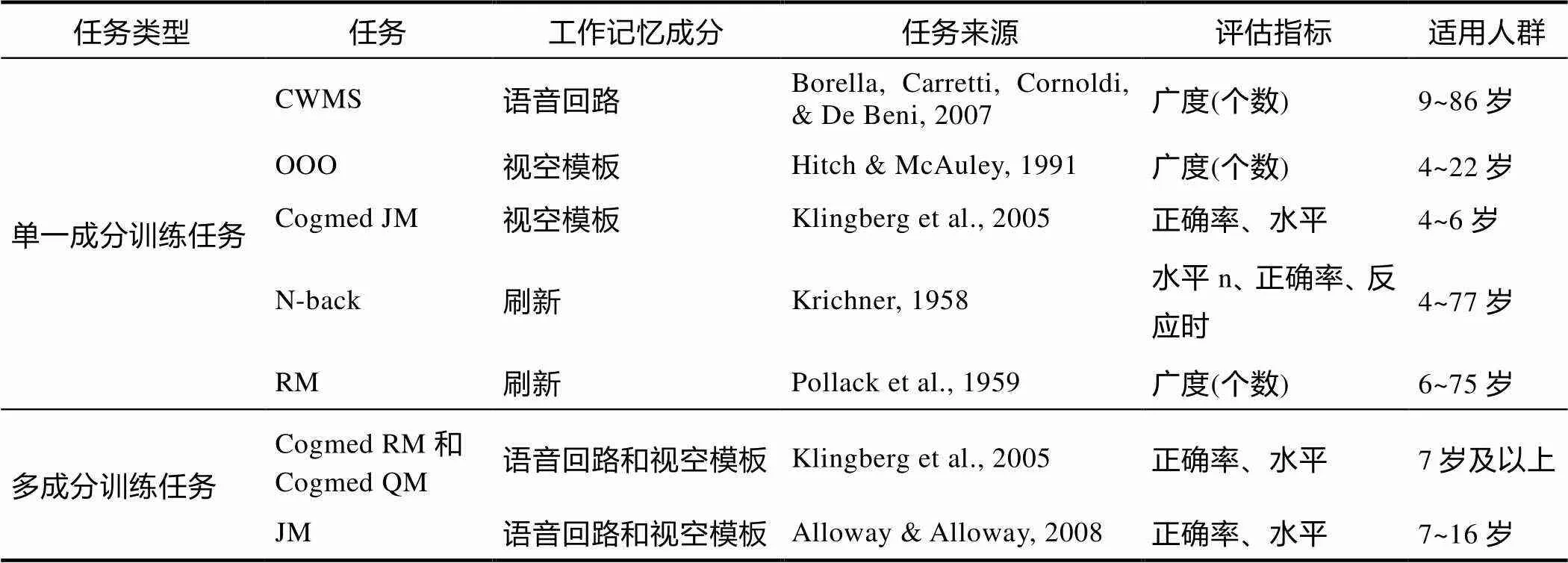
表2 工作记忆的训练任务
注:CWMS=Categorization Working Memory Span; OOO=Odd One Out; RM=Running Memory; JM=Jungle Memory
与数学能力有关的工作记忆训练中常用多任务开展干预, 其中较为常见的训练任务为CWMT和JM, 并且CWMT最被广泛应用, 而另外几个任务更多和其它工作记忆任务结合进行训练。通过对以上任务(概括见表2)的简单介绍, 可以更好理解训练任务类型和训练目标, 从而认识数学能力提高的机制。
3 工作记忆训练对数学能力的提升作用
3.1 数学能力的多维结构
数学能力是一个多维的概念, 涉及包括数感、运算能力和数学推理能力等多个层面(Geary, 2006)。数感是心理表征和操作数字与数量的能力(Friso-van den Bos, Kroesbergen, & van Luit, 2014; Dehaene, 2001), 主要包括数数、数量区分、数轴估计等能力(Jordan, Kaplan, Ola´h, & Locuniak, 2006; Kroesbergen et al., 2012)。运算包括执行计算所需的事实和过程(Brainerd, 1983)。数学推理指对数量关系进行分析以解决问题的能力(Nunes, Bryant, Barros, & Sylva, 2012)。本综述将首先针对以上三种数学能力的工作记忆训练研究进行元分析, 之后再结合元分析结果分别详细介绍三种数学能力的工作记忆训练研究, 以了解工作记忆训练对它们的作用机制。
3.2 工作记忆训练对数学能力作用的元分析
3.2.1 研究方法
(1)文献检索与纳入
在数据库检索平台(PubMed, PsycINFO)对2000~2016年发表的文章进行检索, 检索关键词working memory training和math*、arithmetic*、calculation*、number sense*、reason*的组合。另外, 为了避免遗漏文献, 对当前几篇综述进行文献回溯检索(Melby-Lervåg & Hulme, 2013; Peijnenborgh et al., 2016; Schwaighofer et al., 2015; Titz & Karbach, 2014)。具体检索流程见图8。文献纳入和排除标准为:干预类型为工作记忆训练; 训练效果中包含对数感、运算或数学推理能力的测量, 且在这些测试中可以抽取以上三种数学能力的相关数据以计算效应量; 文献语言为英文; 仅纳入已发表的文章。最终有23篇文献纳入元分析, 具体包括:数感的文献4篇, 运算能力的文献11篇, 数学推理能力的文献10篇, 其中2篇文献同时测量运算能力和数学推理能力。
(2) 调节变量的编码
表3显示调节变量的具体编码。调节变量有助于解释影响训练效果的因素, 参照已有研究的编码方式(Melby-Lervåg & Hulme, 2013; Schwaighofer et al., 2015), 本文将各类调节变量进行如下编码。
(3) 效应量计算
本研究采用Comprehensive Meta-Analysis (Borenstein, Hedges, Higgins, & Rothstein, 2005)进行元分析。采用Cohen’s作为效应量指标, 其中0.8为大效应量, 0.5为中等效应量, 0.2为小效应量。元分析采用随机效应模型(random-effects model)。
3.2.2 工作记忆训练对数感的效果
工作记忆的各个成分在数感任务中均发挥一定作用, 其中语音回路对于言语理解和获得产生作用, 使儿童理解数感任务中对数字的口头指导(Friso-van den Bos et al., 2014)。为正确执行数感任务, 数字表征需要与对应数量相联系, 这种数量表征的空间映射与视空模板相关(Bachot, Gevers, Fias, & Roeyers, 2005; Herrera, Macizo, & Semenza, 2008; Kroesbergen et al., 2014); 并且特定策略的使用也需要视空模板的参与, 如手指数数的策略(Kyttälä, Aunio, Lehto, Van Luit, & Hautamäki, 2003)。中央执行系统在数感任务的提取和存储过程发挥作用, 以数字比较为例, 对于两个不同的数字, 需要使其与对应的数量匹配, 为更准确地执行任务, 这些信息需要被储存起来, 中央执行系统的功能为帮助从长时记忆中提取这些信息, 执行任务时, 帮助整合与更新信息(Kroesbergen et al., 2014)。
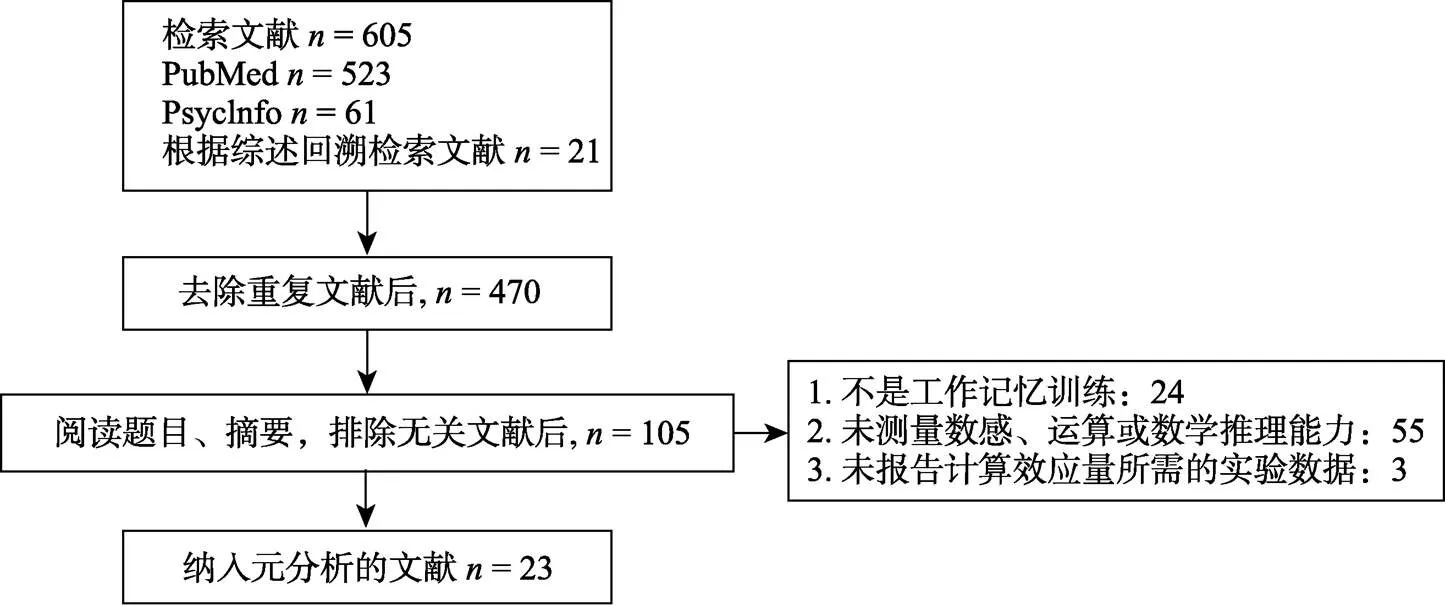
图8 文献检索流程图

表3 调节变量的编码
由于工作记忆与数感之间存在的紧密联系, 因此工作记忆训练对数感能力的作用也受到研究者的关注。一些研究发现, 当进行工作记忆训练时, 不论是正常儿童还是数感能力较低的儿童, 他们的数数、数量比较、数轴任务等成绩都得到了提高(Kroesbergen et al., 2012, 2014; Passolunghi & Costa, 2016)。但是也有研究者对正常儿童进行数数和工作记忆结合进行训练, 结果却显示进行这样训练的被试在数数任务上并没有得到提高(Kyttälä et al., 2015)。具体信息参考电子版附表1。
尽管如此, 研究更为一致的发现是工作记忆训练对数感的改善可能是有效的, 并且在我们元分析的发现也验证了这一点, 尽管研究数量相对有限, 我们发现数感的效应量为中等(Cohen’s= 0.51), 即工作记忆训练可能有效改善数感能力(如表4所示)。同时, 我们也考察训练强度等变量对数感能力改善效果的影响, 然而结果显示这些因素均无法预测效应量的改变(如表5所示), 即这些因素对训练效果的影响较小, 但由于研究数量相对有限, 这一结论需要更多研究验证。
3.2.3 工作记忆训练对运算能力的效果
已有研究表明, 工作记忆参与运算执行的过程中, 包括:工作记忆在运算的表征中发挥作用(Demir, Prado, & Booth, 2014; Rotzer et al., 2009), 比如对于水平呈现的题目人们倾向于使用语音回路进行言语表征, 垂直呈现的题目则使用视空模板进行视觉表征(Caviola, Mammarella, Cornoldi, & Lucangeli, 2012); 影响运算题目信息、中间结果(如29+34, 个位数上9+4=13, 需要将进位的中间结果保持, 并在十位数的运算中提取这个中间结果)及其它暂时信息的存储 (张明, 陈骐, 2006); 影响策略的选择与切换(Hubber, Gilmore, & Cragg, 2014; Wu et al., 2008; 陈英和, 王明怡, 2006; 王明怡, 陈英和, 2006); 抑制无关运算的进行与无关信息的干扰(Cragg & Gilmore, 2014; 陈英和, 耿柳娜, 2004)等等。
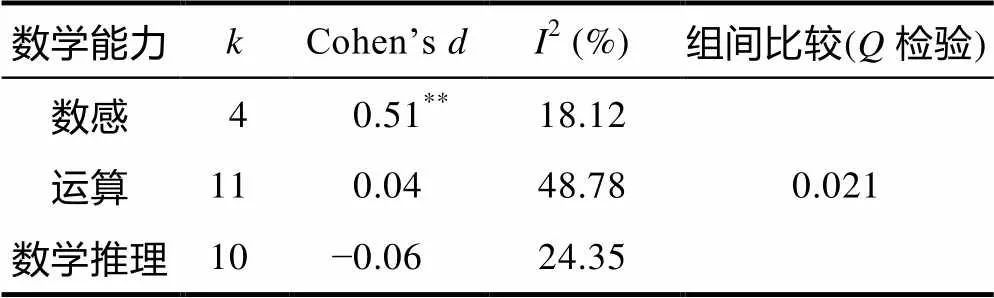
表4 工作记忆训练对数学能力的作用
注:表示纳入研究个数。**< 0.01.
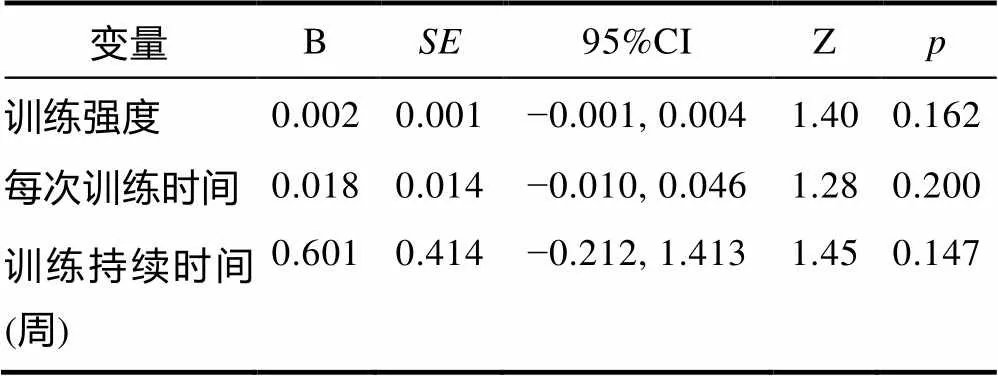
表5 连续的调节变量对数感能力作用的影响
鉴于工作记忆在运算过程的重要作用, 因此很多研究者利用工作记忆设计针对运算能力的训练。不少研究发现了工作记忆训练能够提高运算能力。例如, 对存在轻微智障的儿童进行视空模板任务的训练, 结果发现他们在10周之后运算能力提高了(van der Molen et al., 2010)。此外, 对注意缺陷和数学困难的儿童(Nelwan & Kroesbergen, 2016)、患有工作记忆缺陷的儿童(Bergman-Nutley & Klingberg, 2014)或正常儿童(Söderqvist & Nutley, 2015)进行语音回路和视空模板的训练, 训练均提高了他们的运算表现。当在正常儿童中同时针对工作记忆三个成分进行训练时, 结果发现他们在加法任务中的错误率更低(Witt, 2011)。在这些研究中, 不管是对工作记忆的单一成分, 还是同时对多个成分进行训练, 都发现了训练对于运算能力的积极作用。
但是, 也有很多研究并未验证这个训练的积极效应。有研究对成人进行语音回路或刷新能力的训练, 在正常、注意缺陷多动障碍(Attention Deficit Hyperactivity Disorder, ADHD)或需要接受特殊教育的儿童中进行CWMT训练, 均未能提高他们的运算能力(Dahlin, 2013; Fälth, Jaensson, & Johansson, 2015; Minear et al., 2016; Partanen, Jansson, Lisspers, & Sundin, 2015)。对工作记忆和数学困难的儿童用CWMT与刷新任务进行训练, 结果发现这两种训练均无法提升障碍儿童的运算能力(Ang et al., 2015; Roberts et al., 2016)。有研究甚至对工作记忆的三个系统都进行训练, 但仍然未获有效提升(Kuhn & Holling, 2014)。具体信息参考电子版附表2。类似的, 我们元分析的结果也显示工作记忆训练无法迁移到运算能力, 其改善的效应量小, Cohen’s= 0.04, 这与过去的元分析的发现是一致的(Melby-Lervåg, Redick, & Hulme, 2016; Peijnenborgh et al., 2016)。
由于分类调节变量样本分布较为不均, 如表6所示, 所以本部分仅探究连续的调节变量的作用(见表7), 结果发现训练频率、训练强度、每次训练持续时间和训练持续周数对训练效果没有影响, 已有研究也证实了这些因素对于迁移效果没有作用, 研究者解释可能是由于样本数量太少, 数据统计力低(Melby-Lervåg & Hulme, 2013; Schwaighofer et al., 2015)。
另外, 训练方式的差异可能也会影响训练效果, 比如Kuhn和Holling (2014)与Witt (2011)的研究, 前一项研究采用的是适应性训练, 每天的训练内容一样, 但是任务难度会随被试表现而改变, 训练方式属于核心训练(core training), 即训练目标是工作记忆的内在机制, 任务中需要运用工作记忆资源, 后一项研究中, 学生每周训练的任务不同, 并且学习内容中涉及完成任务的策略, 不仅包括核心训练, 还包括策略训练(strategy training), 策略训练指授予被试有效的编码、保持和提取方法(Morrison & Chein, 2011), 因而后一项研究的训练方式产生的效果更大。但由于在本研究中, 采用后一种训练的研究很少, 因此无法对训练方式进行编码, 分析其作用, 未来还需要更多研究对此进行探讨。
3.2.4 工作记忆训练对数学推理能力的效果
大量研究已经探讨工作记忆对一般推理能力的影响, 通过影响推理过程, 个体将题目信息维持在工作记忆中, 随后利用这些信息确定各单元图形的关系, 做出选择(张清芳, 朱滢, 2000)。研究发现工作记忆的不同成分在不同类型的推理任务中发挥作用各异, 比如视空模板可预测图形推理能力的改善 (Stevenson, Heiser, & Resing, 2013)。通过训练, 增大工作记忆容量, 或者提高使用策略与知识的效率, 便能够提高推理能力。另外, 工作记忆与流体智力有重叠的脑区, 包括侧前额皮层和顶叶皮层(Gray, Chabris, & Braver, 2003; Kane & Engle, 2002), 对这些重合的脑区进行训练, 也能使推理能力得到提升。由于数学推理能力在一般推理能力、数能力(如运算)等能力的基础上发展而来(Geary, 2006), 因此, 工作记忆训练可能也能够提高数学推理能力。
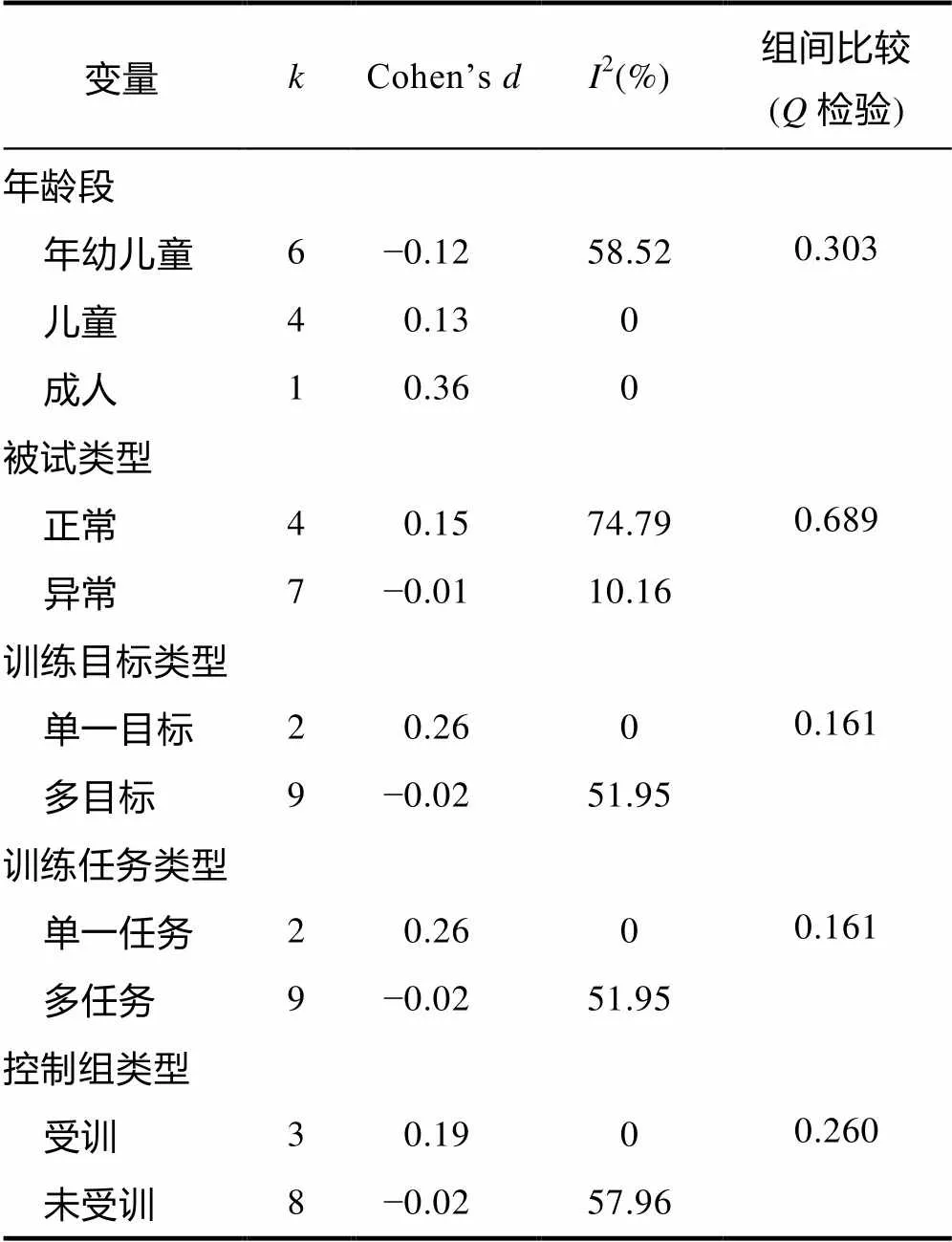
表6 分类调节变量对运算能力作用的影响
注:表示纳入研究个数。
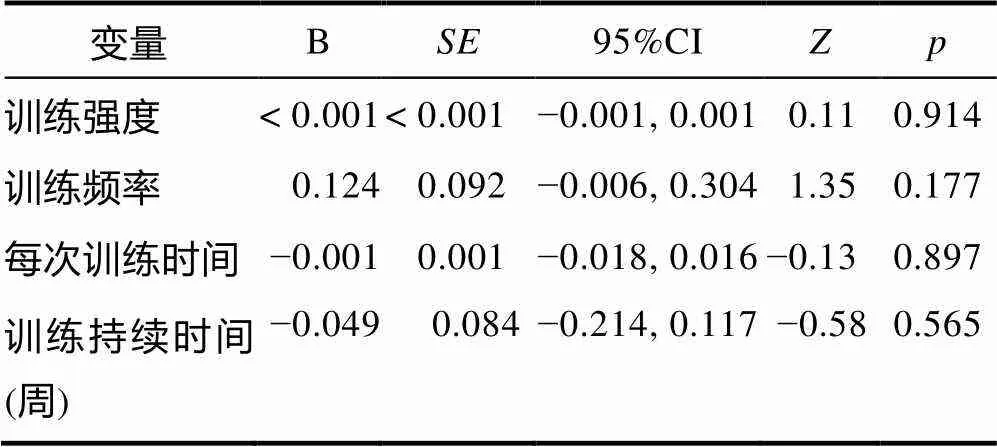
表7 连续的调节变量对运算能力作用的影响
然而, 现有的较少研究表明工作记忆训练能够提高数学推理能力。用听力广度任务对正常儿童进行训练, 8次之后, 他们的数学推理能力提高了, 并且效果保持到3个月后(Cornoldi, Carretti, Drusi, & Tencati, 2015)。在异常儿童中, 如学习困难儿童或低工作记忆能力的儿童, 用JM或CWMT任务进行语音回路和视空模板的训练, 也得到了积极的结果(Alloway, 2012; Holmes, Gathercole, & Dunning, 2009)。但是, 更多的研究发现这样的训练对数学推理能力没有提升作用, 无论是正常(Harrison et al., 2013; Mansur-Alves & Flores- Mendoza, 2015; Redick et al., 2013; Rode, Robson, Purviance, Geary, & Mayr, 2014)还是异常(Alloway et al., 2013; Dunning et al., 2013; Phillips et al., 2016)个体都是如此。具体信息参考电子版附表3。
在本研究元分析的结果中, 同样显示工作记忆训练无法改善数学推理能力, Cohen’s= −0.06, 这与前人的发现一致(Melby-Lervåg & Hulme, 2013)。这可能是因为很多研究的训练目标主要集中在语音回路和视空模板, 而不是中央执行系统, 而过去有元分析表明刷新能力与数学表现之间存在着较强的联系(Friso-van den Bos et al., 2013), 刷新训练能够改善一般推理能力(Au et al., 2015)。因此未来关于提升数学推理能力的研究应该更专注于利用中央执行系统的训练。
进一步分析调节变量的作用, 发现多目标训练效果可能差于单一目标训练效果(见表8, 单一目标:Cohen’s= 0.07, 多目标:Cohen’s= −0.24,= 0.060 )。这与已有研究结果不一致(Schwaighofer et al., 2015), 尽管对工作记忆多个系统进行训练, 可以增加训练和迁移情境之间的相似性, 但若是受训者无法对各种混合情境进行正确辨认, 则可能会减弱它的作用, 甚至损害训练的效果。研究还发现其它调节因素(如年龄段、被试类型等)均不影响训练的迁移效果, 但也有一些研究却发现10岁以上的儿童能够在言语工作记忆上获益更多, 但这一特点并没有体现在数学推理能力上, 这可能是因为迁移到与工作记忆较为不一致的任务中, 其难度更大, 无法体现出年龄上的优势(Peijnenborgh et al., 2015)。Titz和Karbach (2014)则认为低能力个体在工作记忆训练中能获益更多, 但我们的元分析并未验证这一观点。另外, 虽然研究中发现训练任务类型和控制组类型对训练效果没有影响, 但是由于样本差异较大, 需谨慎对待。最后, 训练强度、训练频率和训练持续时间对干预效果的影响(见表9)与已有研究的发现较为一致(Melby-Lervåg & Hulme, 2013; Schwaighofer et al., 2015), 它们对于远迁移的作用较为有限。训练持续周数对数学推理能力也没有影响, 这或许是因为对于数学推理能力的工作训练持续时间较为接近, 变异性低, 因此无法体现它的作用。
综上所述, 工作记忆训练对数感可能具有改善作用, 效应量为中等(Cohen’s= 0.51), 而在运算和数学推理能力中工作记忆训练则无积极作用。此外, 训练目标会影响数学能力的改善效果。但值得注意的是, 由于研究数量的有限, 对这些分析所得出的结论需谨慎看待, 未来还需要更多的研究来探讨这些变量的作用。
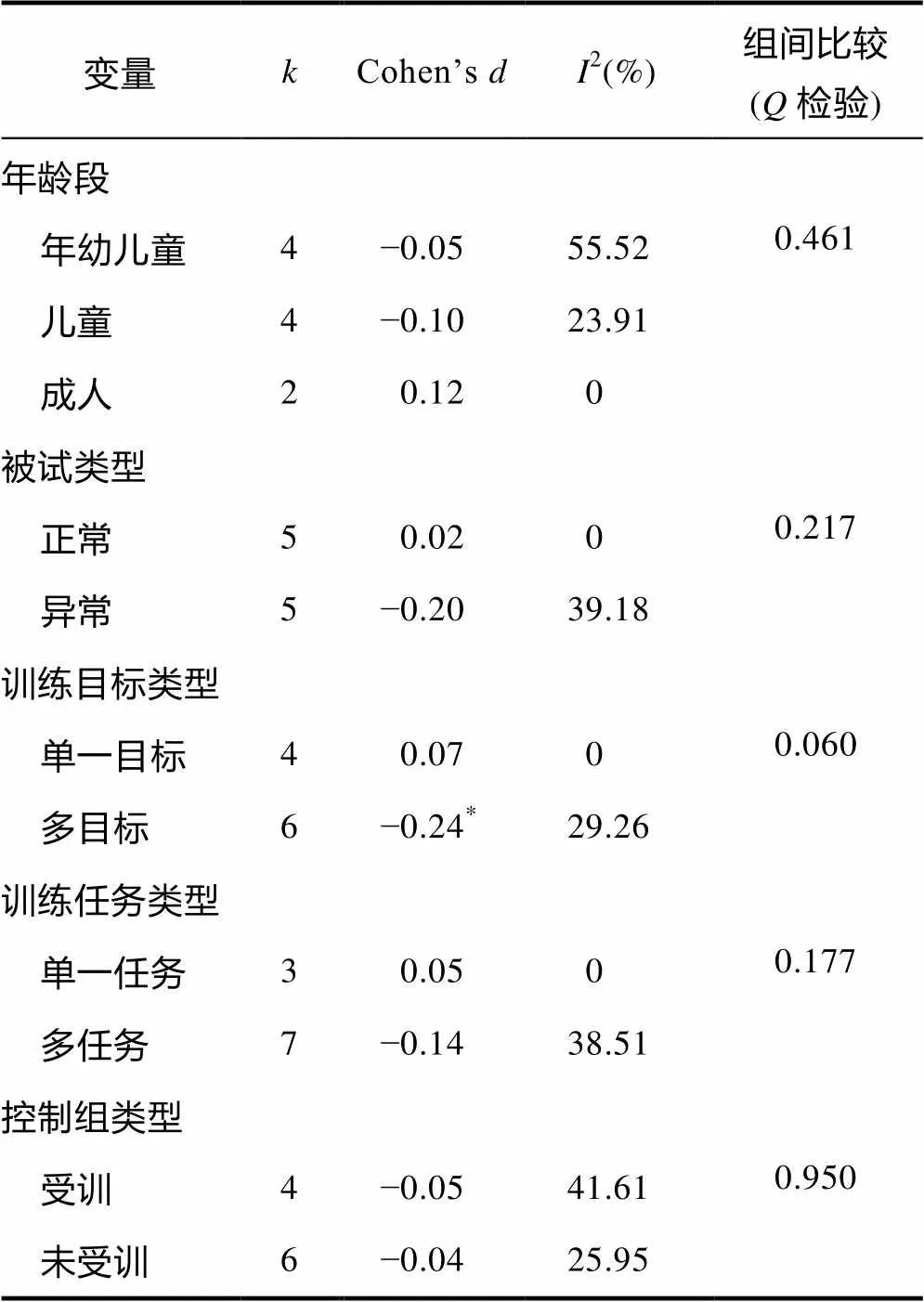
表8 分类调节变量对数学推理能力作用的影响
注:表示纳入研究个数。*< 0.05.
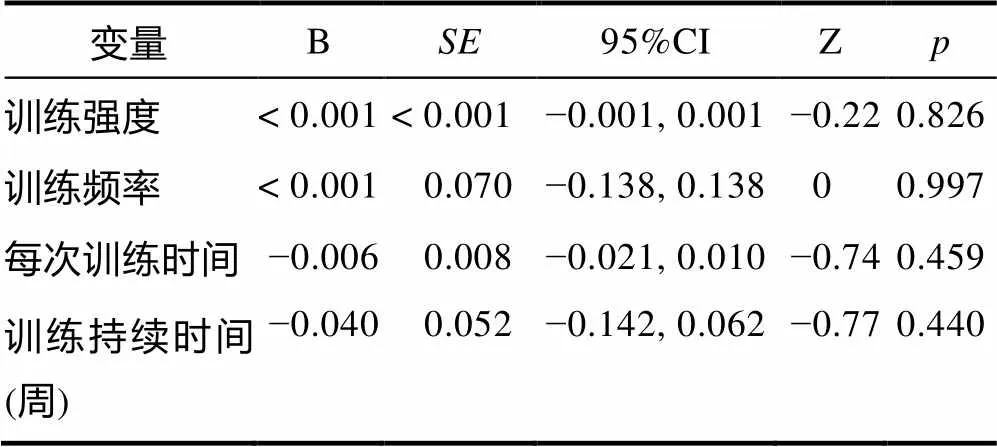
表9 连续的调节变量对数学推理能力作用的影响
尽管本研究发现工作记忆训练可能对数感具有改善作用, 但是数感能力为什么得到提升的背后机制还不是非常清楚, 值得深入探讨。另外, 鉴于导致数学障碍的原因之一是数感能力的缺陷, 因此是否能够通过工作记忆训练改善数感能力, 从而对数学障碍有所缓解, 这也是值得进一步探讨的方向。
本研究发现了训练任务所针对的目标会影响训练效果, 但是依然存在很多问题需要进一步探讨, 比如, 训练方法的有效性, 训练任务是否准确触及了所针对的工作记忆能力?不同目标的训练方式对于提高数学能力究竟存在哪些不同影响。由于过去的研究很多都采用多维度任务进行训练, 因此我们很难判断究竟哪些训练更为有效, 或者完全无关哪个训练任务, 而是取决于不同训练任务叠加训练效应。这些问题同样需要今后大量的实证研究进行探讨。
(*为纳入元分析文献)
陈英和, 耿柳娜. (2004). 工作记忆与算术认知的研究现状与前瞻.(1), 40–44.
陈英和, 王明怡. (2006). 工作记忆广度对儿童算术认知策略的影响.(2), 29–35.
黎翠红, 何旭, 郭春彦. (2014). 工作记忆训练的研究述评.(3), 407–412.
刘春雷, 周仁来. (2012). 工作记忆训练对认知功能和大脑神经系统的影响.(7), 1003–1011.
王明怡, 陈英和. (2006). 工作记忆中央执行对儿童算术认知策略的影响.(4), 24–28.
张明, 陈骐. (2006). 工作记忆子成分在听觉障碍儿童心算过程中的作用.(1), 76–79.
张清芳, 朱滢. (2000). 工作记忆和推理.(1), 12–17.
赵鑫, 王一雪, 刘丹玮, 周仁来. (2011). 工作记忆刷新训练对儿童流体智力的影响.(17), 1345–1348.
*Alloway, T. (2012). Can interactive working memory training improve learning.(3), 197–207.
Alloway, T. P., & Alloway, R. G. (2008).. Edinburgh, United Kingdom: Memosyne.
Alloway, T. P., Gathercole, S. E., Kirkwood, H., & Elliott, J. (2008). Evaluating the validity of the Automated Working Memory Assessment.(7), 725–734.
*Alloway, T. P., Bibile, V., & Lau, G. (2013). Computerized working memory training: Can it lead to gains in cognitive skills in students?(3), 632–638.
*Ang, S. Y., Lee, K., Cheam, F., Poon, K., & Koh, J. (2015). Updating and working memory training: Immediate improvement, long-term maintenance, and generalisability to non-trained tasks.(2), 121–128.
Au, J., Sheehan, E., Tsai, N., Duncan, G. J., Buschkuehl, M., & Jaeggi, S. M. (2015). Improving fluid intelligence with training on working memory: A meta-analysis.(2), 366–377.
Bachot, J., Gevers, W., Fias, W., & Roeyers, H. (2005). Number sense in children with visuospatial disabilities: Orientation of the mental number line., 172–183.
*Bergman-Nutley, S., & Klingberg, T. (2014). Effect of working memory training on working memory, arithmetic and following instructions.(6), 869–877.
Borella, E., Carretti, B., Cornoldi, C., & De Beni, R. (2007). Working memory, control of interference and everyday experience of thought interference: When age makes the difference.(3), 200–206.
Borella, E., Carretti, B., & De Beni, R. (2008). Working memory and inhibition across the adult life-span.(1), 33–44.
Borella, E., Carretti, B., Riboldi, F., & De Beni, R. (2010). Working memory training in older adults: Evidence of transfer and maintenance effects.(4), 767–778.
Borenstein, M., Hedges, L., Higgins, J., & Rothstein, H. (2005).(Version 2) [Software]. Engelwood, NJ: Biostat.
Brainerd, C. J. (1983). Young children's mental arithmetic errors: A working-memory analysis.(4), 812–830.
Carretti, B., Cornoldi, C., De Beni, R., & Palladino, P. (2004). What happens to information to be suppressed in working-memory tasks? Short and long term effects.(6), 1059–1084.
Caviola, S., Mammarella, I. C., Cornoldi, C., & Lucangeli, D. (2012). The involvement of working memory in children's exact and approximate mental addition.(2), 141–160.
*Cornoldi, C., Carretti, B., Drusi, S., & Tencati, C. (2015). Improving problem solving in primary school students: The effect of a training programme focusing on metacognition and working memory.(3), 424–439.
Cragg, L., & Gilmore, C. (2014). Skills underlying mathematics: The role of executive function in the development of mathematics proficiency.(2), 63–68.
*Dahlin, K. I. E. (2013). Working memory training and the effect on mathematical achievement in children with attention deficits and special needs.(1), 118–133.
Dehaene, S. (2001). Précis of the number sense.(1), 16–36.
Demir, Ö. E., Prado, J., & Booth, J. R. (2014). The differential role of verbal and spatial working memory in the neural basis of arithmetic.(6), 440–458.
*Dunning, D. L., Holmes, J., & Gathercole, S. E. (2013). Does working memory training lead to generalized improvements in children with low working memory? A randomized controlled trial.(6), 915–925.
*Fälth, L., Jaensson, L., & Johansson, K. (2015). Working memory training – A Cogmed intervation.(2), 28–35.
Friso-van den Bos, I., Kroesbergen, E. H., & van Luit, J. E. H. (2014). Number sense in kindergarten children: Factor structure and working memory predictors., 23–29.
Friso-van den Bos, I., van der Ven, S. H. G., Kroesbergen, E. H., & van Luit, J. E. H. (2013). Working memory and mathematics in primary school children: A meta-analysis., 29–44.
Geary, D. C. (2006). Development of mathematical understanding. In W. Damon, R. M. Lerner, D. Kuhn, & R. S. Sielger (Eds.),(6th ed., pp.777– 810). New York: Wiley.
Giofrè, D., Mammarella, I. C., & Cornoldi, C. (2013). The structure of working memory and how it relates to intelligence in children.(5), 396–406.
Gray, J. R., Chabris, C. F., & Braver, T. S. (2003). Neural mechanisms of general fluid intelligence.(3), 316–322.
Harrison, T. L., Shipstead, Z., Hicks, K. L., Hambrick, D. Z., Redick, T. S., & Engle, R. W. (2013). Working memory training may increase working memory capacity but not fluid intelligence.(12), 2409–2419.
Henry, L. A. (2001). How does the severity of a learning disability affect working memory performance?(4–6), 233–247.
Herrera, A., Macizo, P., & Semenza, C. (2008). The role of working memory in the association between number magnitude and space.(2), 225–237.
Hitch, G. J., & McAuley, E. (1991). Working memory in children with specific arithmetical learning difficulties.(3), 375–386.
*Holmes, J., Gathercole, S. E., & Dunning, D. L. (2009). Adaptive training leads to sustained enhancement of poor working memory in children.(4), F9–F15.
Hubber, P. J., Gilmore, C., & Cragg, L. (2014). The roles of the central executive and visuospatial storage in mental arithmetic: A comparison across strategies.(5), 936–954.
Jaeggi, S. M., Buschkuehl, M., Jonides, J., & Perrig, W. J. (2008). Improving fluid intelligence with training on working memory.(19), 6829– 6833.
Jaeggi, S. M., Buschkuehl, M., Jonides, J., & Shah, P. (2011). Short- and long-term benefits of cognitive training.(25), 10081–10086.
Jahanshahi, M., Saleem, T., Ho, A. K, Fuller, R., & Dirnberger, G. (2008). A preliminary investigation of the running digit span as a test of working memory.(1–2), 17–25.
Jordan, N. C., Kaplan, D., Ola´h, L. N., & Locuniak, M. N. (2006). Number sense growth in kindergarten: A longitudinal investigation of children at risk for mathematics difficulties.(1), 153–175.
Kane, M. J., & Engle, R. W. (2002). The role of prefrontal cortex in working-memory capacity, executive attention, and general fluid intelligence: An individual-differences perspective.(4), 637–671.
Klingberg, T., Fernell, E., Olesen, P., J., Johnson, M., Gustafsson, P., Dahlström, K., … Westerberg, H. (2005). Computerized training of working memory in children with ADHD: A randomized, controlled trial.(2), 177–186
Krichner, W. K. (1958). Age differences in short-term retention of rapidly changing information.(4), 352–358.
*Kroesbergen, E. H., Van't Noordende, J. E., & Kolkman, M. E. (2012). Number sense in low-performing kindergarten children: Effects of a working memory and an early math training. In: Z. Breznitz, O. Rubinsten, V. Molfese, & D. Molfese (Eds.),(pp. 295–313). Netherlands: Springer.
*Kroesbergen, E. H., Van't Noordende, J. E., & Kolkman, M. E. (2014). Training working memory in kindergarten children: Effects on working memory and early numeracy.(1), 23–37.
Kuhn, J.-T., & Holling, H. (2014). Number sense or working memory? The effect of two computer-based trainings on mathematical skills in elementary school.(2), 59–67.
Kyttälä, M., Aunio, P., Lehto, J. E., Van Luit, J., & Hautamäki, J. (2003). Visuospatial working memory and early numeracy.(3), 65–76.
*Kyttälä, M., Kanerva, K., & Kroesbergen, E. (2015). Training counting skills and working memory in preschool.(4), 363–370.
*Mansur-Alves, M., & Flores-Mendoza, C. (2015). Working memory training does not improve intelligence: Evidence from Brazilian children.(3), 474–482.
Melby-Lervåg, M., & Hulme, C. (2013). Is working memory training effective? A meta-analytic review.(2), 270–291.
Melby-Lervåg, M., Redick, T. S., & Hulme, C. (2016). Working memory training does not improve performance on measures of intelligence or other measures of "far transfer": Evidence from a meta-analytic review.(4), 512–534.
*Minear, M., Brasher, F., Guerrero, C. B., Brasher, M., Moore, A., & Sukeena, J. (2016). A simultaneous examination of two forms of working memory training: Evidence for near transfer only.(7), 1014–1037.
Morrison, A. B., & Chein, J. M. (2011). Does working memory training work? The promise and challenges of enhancing cognition by training working memory.(1), 46–60.
*Nelwan, M., & Kroesbergen, E. H. (2016). Limited near and far transfer effects of Jungle Memory working memory training on learning mathematics in children with attentional and mathematical difficulties., 1384.
Nunes, T., Bryant, P., Barros, R., & Sylva, K. (2012). The relative importance of two different mathematical abilities to mathematical achievement., 136–156.
*Partanen, P., Jansson, B., Lisspers, J., & Sundin, Ö. (2015). Metacognitive strategy training adds to the effects of working memory training in children with special educational needs.(3), 130–140.
*Passolunghi, M. C., & Costa, H. M. (2016). Working memory and early numeracy training in preschool children.(1), 81–98.
Peijnenborgh, J. C., Hurks, P. M., Aldenkamp, A. P., Vles, J. S.., & Hendriksen, J. G. M. (2016). Efficacy of working memory training in children and adolescents with learning disabilities: A review study and meta-analysis.(5–6), 645–672.
Phillips, N. L., Mandalis, A., Benson, S., Parry, L., Epps, A., Morrow, A., & Lah, S. (2016). Computerized working memory training for children with moderate to severe traumatic brain injury: A double-blind, randomized, placebo-controlled trial.(23), 2097–2104.
Pollack, I., Johnson, L. B., & Knaff, P. R. (1959). Running memory span.(3), 137–146.
Raghubar, K. P., Barnes, M. A., & Hecht, S. A. (2010). Working memory and mathematics: A review of developmental, individual difference, and cognitive approaches.(2), 110–122.
*Redick, T. S., Shipstead, Z., Harrison, T. L., Hicks, K. L., Fried, D. E., Hambrick, D. Z., ... Engle, R. W. (2013). No evidence of intelligence improvement after working memory training: A randomized, placebo-controlled study.(2), 359–379.
*Roberts, G., Quach, J., Spencer-Smith, M., Anderson, P. J., Gathercole, S., Gold, L., ... Wake, M. (2016). Academic outcomes 2 years after working memory training for children with low working memory: A randomized clinical trial.(5), e154568.
*Rode, C., Robson, R., Purviance, A., Geary, D. C., & Mayr, U. (2014). Is working memory training effective? A study in a school setting.(8), e104796.
Rotzer, S., Loenneker, T., Kucian, K., Martin, E., Klaver, P., & von Aster, M. (2009). Dysfunctional neural network of spatial working memory contributes to developmental dyscalculia.(13), 2859–2865.
*Söderqvist, S., & Nutley, S. B. (2015). Working memory training is associated with long term attainments in math and reading., 1711.
Schwaighofer, M., Fischer, F., & Bühner, M. (2015). Does working memory training transfer? A meta-analysis including training conditions as moderators.(2), 138–166.
Stevenson, C. E., Heiser, W. J., & Resing, W. C. M. (2013). Working memory as a moderator of training and transfer of analogical reasoning in children.(3), 159–169.
Titz, C., & Karbach, J. (2014). Working memory and executive functions: Effects of training on academic achievement., 852–868.
*van der Molen, M. J., van Luit, J. E., van der Molen, M. W., Klugkist, I., & Jongmans, M. J. (2010). Effectiveness of a computerised working memory training in adolescents with mild to borderline intellectual disabilities.(5), 433–447.
von Bastian, C. C., Langer, N., Jäncke, L., & Oberauer, K. (2013). Effects of working memory training in young and old adults.(4), 611–624.
*Witt, M. (2011). School based working memory training: Preliminary finding of improvement in children's mathematical performance., 7–15.
Wu, S. S., Meyer, M. L., Maeda, U., Salimpoor, V., Tomiyama, S., Geary, D. C., & Menon, V. (2008). Standardized assessment of strategy use and working memory in early mental arithmetic performance.(3), 365–393.
附录:
附表1 工作记忆训练对数感影响的研究总结列表
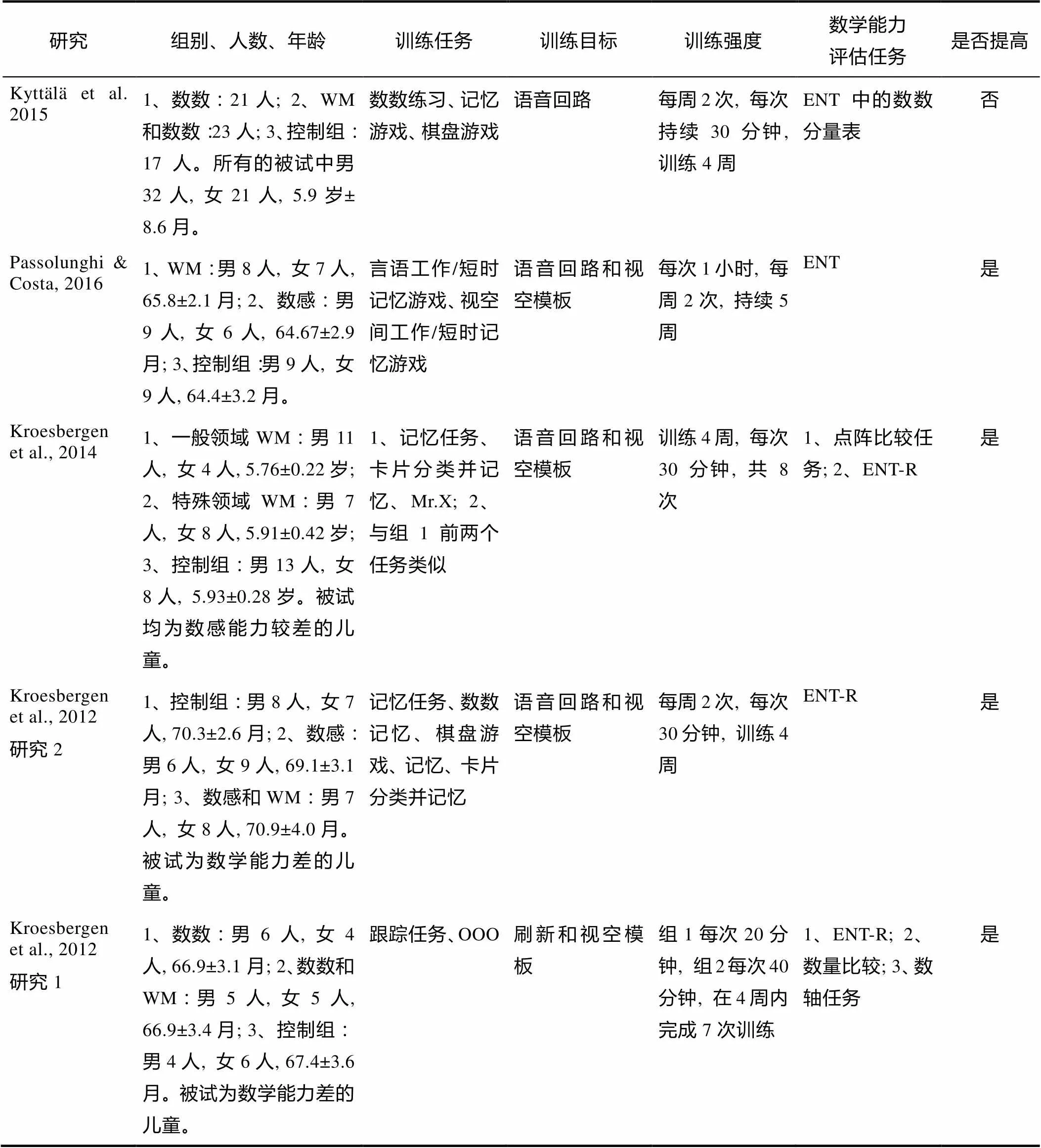
研究组别、人数、年龄训练任务训练目标训练强度数学能力评估任务是否提高 Kyttälä et al. 20151、数数:21人; 2、WM和数数:23人; 3、控制组:17人。所有的被试中男32人, 女21人, 5.9岁± 8.6月。数数练习、记忆游戏、棋盘游戏语音回路每周2次, 每次持续30分钟, 训练4周ENT中的数数分量表否 Passolunghi & Costa, 20161、WM:男8人, 女7人, 65.8±2.1月; 2、数感:男9人, 女6人, 64.67±2.9月; 3、控制组:男9人, 女9人, 64.4±3.2月。言语工作/短时记忆游戏、视空间工作/短时记忆游戏语音回路和视空模板每次1小时, 每周2次, 持续5周ENT是 Kroesbergen et al., 20141、一般领域WM:男11人, 女4人, 5.76±0.22岁; 2、特殊领域WM:男7人, 女8人, 5.91±0.42岁; 3、控制组:男13人, 女8人, 5.93±0.28岁。被试均为数感能力较差的儿童。1、记忆任务、卡片分类并记忆、Mr.X; 2、与组1前两个任务类似语音回路和视空模板训练4周, 每次30分钟, 共8 次1、点阵比较任务; 2、ENT-R是 Kroesbergen et al., 2012研究21、控制组:男8人, 女7人, 70.3±2.6月; 2、数感:男6人, 女9人, 69.1±3.1月; 3、数感和WM:男7人, 女8人, 70.9±4.0月。被试为数学能力差的儿童。记忆任务、数数记忆、棋盘游戏、记忆、卡片分类并记忆语音回路和视空模板每周2次, 每次30分钟, 训练4周ENT-R 是 Kroesbergen et al., 2012研究11、数数:男6人, 女4人, 66.9±3.1月; 2、数数和WM:男5人, 女5人, 66.9±3.4月; 3、控制组:男4人, 女6人, 67.4±3.6月。被试为数学能力差的儿童。跟踪任务、OOO刷新和视空模板组1每次20分钟, 组2每次40分钟, 在4周内完成7次训练1、ENT-R; 2、数量比较; 3、数轴任务是
注:WM=Working Memory; ENT= Early Numeracy Test; ENT-R= Early Numeracy Test-Revised; OOO=Odd One Out. 以上研究未探讨训练后效
附表2 工作记忆训练对运算能力影响的研究总结列表
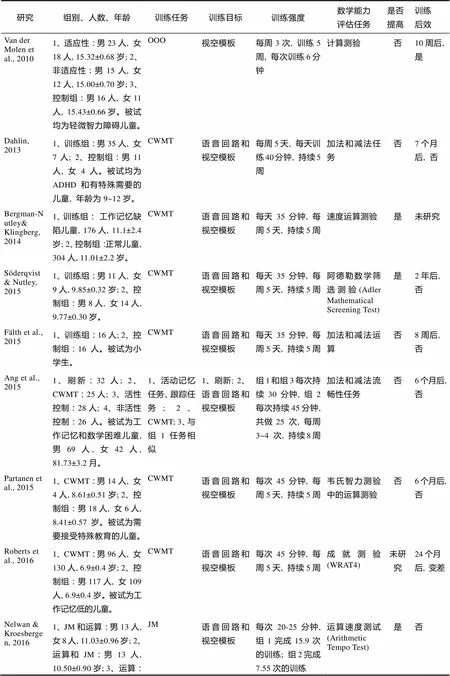
研究组别、人数、年龄训练任务训练目标训练强度数学能力评估任务是否提高训练后效 Van der Molen et al., 20101、适应性:男23人, 女18人, 15.32±0.68岁; 2、非适应性:男15人, 女12人, 15.00±0.70岁; 3、控制组:男16人, 女11人, 15.43±0.66岁。被试均为轻微智力障碍儿童。OOO视空模板每周3次, 训练5周, 每次训练6分钟计算测验否10周后, 是 Dahlin, 20131、训练组:男35人, 女7人; 2、控制组:男11人, 女4人。被试均为ADHD和有特殊需要的儿童, 年龄为9~12岁。CWMT语音回路和视空模板每周5天, 每天训练40分钟, 持续5周加法和减法任务否7个月后, 否 Bergman-Nutley& Klingberg, 20141、训练组:工作记忆缺陷儿童, 176人, 11.1±2.4岁; 2、控制组:正常儿童, 304人, 11.01±2.2岁。CWMT语音回路和视空模板每天35分钟, 每周5天, 持续5周速度运算测验是未研究 Söderqvist & Nutley, 20151、训练组:男11人, 女9人, 9.85±0.32岁; 2、控制组:男8人, 女14人, 9.77±0.30岁。CWMT语音回路和视空模板每天35分钟, 每周5天, 持续5周阿德勒数学筛选测验(Adler Mathematical Screening Test)是2年后, 否 Fälthet al., 20151、训练组:16人; 2、控制组:16人。被试为小学生。CWMT语音回路和视空模板每天35分钟, 每周5天, 持续5周加法和减法运算否8周后, 否 Ang et al., 20151、刷新:32人; 2、CWMT:25人; 3、活性控制:28人; 4、非活性控制:26人。被试为工作记忆和数学困难儿童, 男69人, 女42人, 81.73±3.2月。1、活动记忆任务、跟踪任务; 2、CWMT; 3、与组1任务相似1、刷新; 2、语音回路和视空模板组1和组3每次持续30分钟, 组2每次持续45分钟, 共做25 次, 每周3~4 次, 持续8周加法和减法流畅性任务否6个月后, 否 Partanen et al., 20151、CWMT:男14人, 女4人, 8.61±0.51岁; 2、控制组:男18人, 女6人, 8.41±0.57岁。被试为需要接受特殊教育的儿童。CWMT语音回路和视空模板每次45分钟, 每周5天, 持续5周韦氏智力测验中的运算测验否6个月后, 否 Roberts et al., 20161、CWMT:男96人, 女130人, 6.9±0.4岁; 2、控制组:男117人, 女109人, 6.9±0.4岁。被试为工作记忆低的儿童。CWMT语音回路和视空模板每次45分钟, 每周5天, 持续5周成就测验(WRAT4)未研究24个月后, 变差 Nelwan & Kroesbergen, 20161、JM和运算:男13人, 女8人, 11.03±0.96岁; 2、运算和JM:男13人, 10.50±0.90岁; 3、运算:男15人, 女4人, 10.86±1.00岁。被试为注意和数学困难的儿童。JM语音回路和视空模板每次20-25分钟, 组1完成15.9次的训练; 组2完成7.55次的训练运算速度测试(Arithmetic Tempo Test)是否
续表2
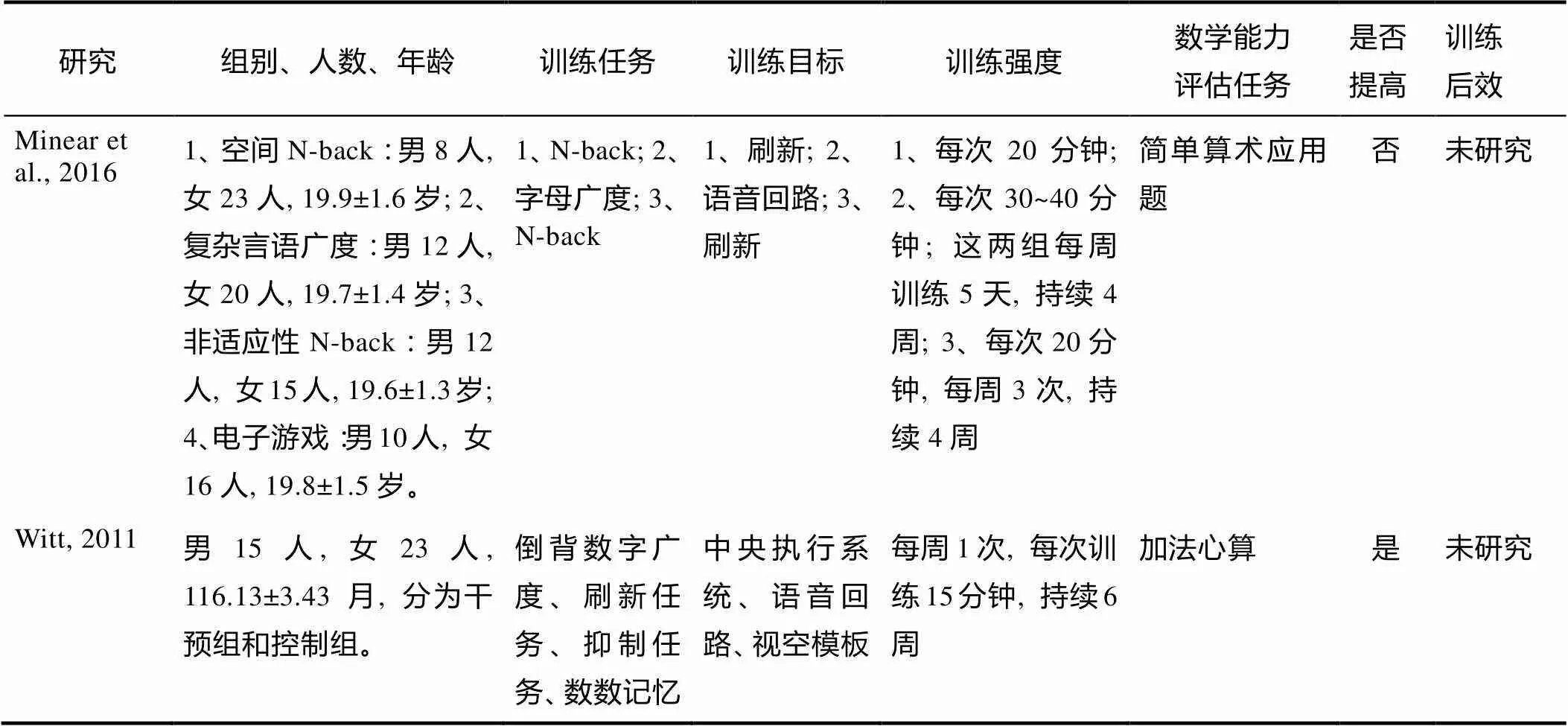
研究组别、人数、年龄训练任务训练目标训练强度数学能力评估任务是否提高训练后效 Minear et al., 20161、空间N-back:男8人, 女23人, 19.9±1.6岁; 2、复杂言语广度:男12人, 女20人, 19.7±1.4岁; 3、非适应性N-back:男12人, 女15人, 19.6±1.3岁; 4、电子游戏:男10人, 女16人, 19.8±1.5岁。1、N-back; 2、字母广度; 3、N-back1、刷新; 2、语音回路; 3、刷新1、每次20分钟; 2、每次30~40分钟; 这两组每周训练5天, 持续4周; 3、每次20分钟, 每周3次, 持续4周简单算术应用题否未研究 Witt, 2011男15人, 女23人, 116.13±3.43月, 分为干预组和控制组。倒背数字广度、刷新任务、抑制任务、数数记忆中央执行系统、语音回路、视空模板每周1次, 每次训练15分钟, 持续6周加法心算是未研究
注:OOO=Odd One Out; ADHD=Attention Deficit Hyperactivity Disorder; CWMT=Cogmed Working Memory Training; WRAT4=Wide Range Achievement Test-4th ed; JM=Jungle Memory
附表3 工作记忆训练对推理能力影响的研究总结列表
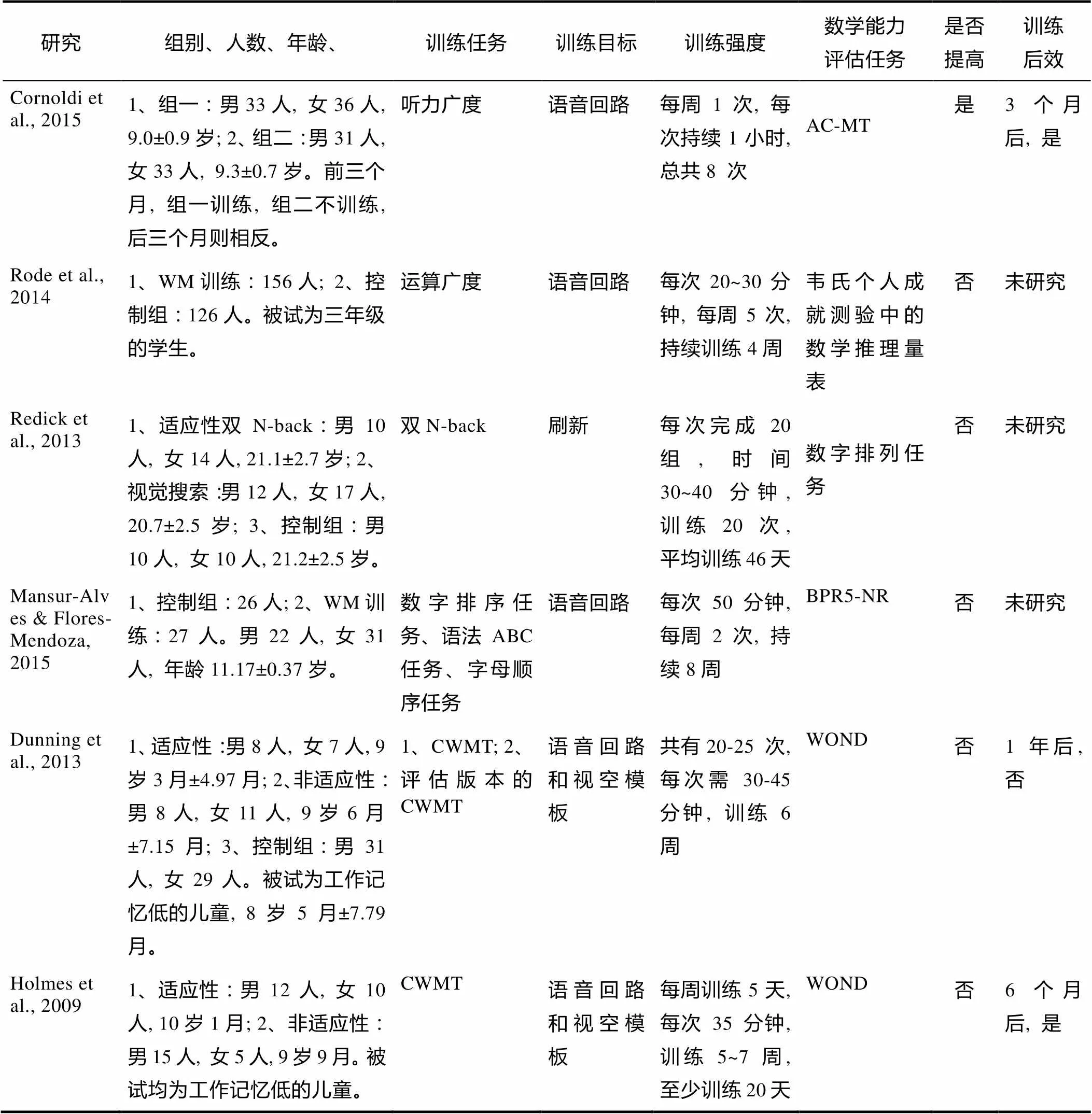
研究组别、人数、年龄、训练任务训练目标训练强度数学能力评估任务是否提高训练后效 Cornoldi et al., 20151、组一:男33人, 女36人, 9.0±0.9岁; 2、组二:男31人, 女33人, 9.3±0.7岁。前三个月, 组一训练, 组二不训练, 后三个月则相反。听力广度语音回路每周1次, 每次持续1小时, 总共8 次AC-MT 是3个月后, 是 Rode et al., 20141、WM训练:156人; 2、控制组:126人。被试为三年级的学生。运算广度语音回路每次20~30分钟, 每周5次, 持续训练4周韦氏个人成就测验中的数学推理量表否未研究 Redick et al., 20131、适应性双N-back:男10人, 女14人, 21.1±2.7岁; 2、视觉搜索:男12人, 女17人, 20.7±2.5岁; 3、控制组:男10人, 女10人, 21.2±2.5岁。双N-back 刷新每次完成20 组, 时间30~40分钟, 训练20 次, 平均训练46天数字排列任务否未研究 Mansur-Alves & Flores- Mendoza, 20151、控制组:26人; 2、WM训练:27人。男22人, 女31人, 年龄11.17±0.37岁。数字排序任务、语法ABC任务、字母顺序任务语音回路每次50分钟, 每周2次, 持续8周BPR5-NR 否未研究 Dunning et al., 20131、适应性:男8人, 女7人, 9岁3月±4.97月; 2、非适应性:男8人, 女11人, 9岁6月±7.15月; 3、控制组:男31人, 女29人。被试为工作记忆低的儿童, 8岁5月±7.79月。1、CWMT; 2、评估版本的CWMT语音回路和视空模板共有20-25 次, 每次需30-45分钟, 训练6周WOND否1年后, 否 Holmes et al., 20091、适应性:男12人, 女10人, 10岁1月; 2、非适应性:男15人, 女5人, 9岁9月。被试均为工作记忆低的儿童。CWMT 语音回路和视空模板每周训练5天, 每次35分钟, 训练5~7周, 至少训练20天WOND否6个月后, 是
续表3
注:AC-MT=Assessment of arithmetic and problem solving skills; WM=Working Memory; BPR5-NR=Brazilian Cognitive Reasoning Battery-Numerical Reasoning; CWMT=Cogmed Working Memory Training; WOND=Wechsler Objective Numerical Dimension; JM=Jungle Memory
Enhancing mathematical abilities: A meta-analysis on the effect of working memory training
GUO Liyue; YAN Chao; DENG Ciping
(School of Psychology and Cognitive Science, East China Normal University, Shanghai 200062, China)
Working memory training can effectively improve individual’s cognitive performance. In last decades, accumulating studies examined the transfer effects of working memory training on the mathematical abilities. However, findings from these studies render inconsistent depending on the measure of mathematical abilities, types of working memory training, and participants. In this meta-analysis, we thus reviewed two types of trainings strategies–uni-dimensional and multi-dimensional trainings – and their effects on the enhancement of mathematical skills, including number sense, arithmetic and mathematics reasoning. Results showed that working memory training significantly improved number sense with a medium effect size (Cohen’s= 0.51), rather than arithmetic (Cohen’s= 0.04) and mathematics reasoning (Cohen’s=-0.06). Furthermore, the types of working memory training significantly moderated the transfer effects of working memory training on mathematical performance.
working memory training; mathematical ability; number sense; arithmetic; mathematical reasoning
B849:G44
2017-07-10
* 国家自然科学基金面上项目(项目编号71373081); 国家自然科学基金青年项目(项目编号31500894)。
严超, E-mail: cyan@psy.ecnu.edu.cn; 邓赐平, E-mail: cpdeng@psy.ecnu.edu.cn
10.3724/SP.J.1042.2018.01576

