基于有限元法的悬架系统振动传递函数研究

徐寅生，岳涛

（安徽江淮汽车集团股份有限公司，安徽 合肥 230601）

引言

悬架是车身与车桥间一切传力连接的装置，弹性地连接车体和车轮，缓和并衰减由于路面不平度传递至车辆的振动[1]，合理的悬架振动传递特性设计，达成较好的隔振性能，可以避免车轮的振动过大的通过悬架，传递至车身，减小车身结构振动，降低车内噪声，提升悬架NVH特性。

1 基本理论

1.1 有限元法

有限元法是用有限个单元将结构弹性体或空气离散化，根据力学或声学方程，得到联立代数方程并求解，得到结构振动特性或声学特性，适用于低频振动模拟和分析。对系统进行有限元分析，预测振动传递特性，通过分析结果对设计方案进行优化，提高设计水平。

1.2 传递路径分析法

传递路径分析法就是复杂系统受到多种振动噪声源激励，每种激励都可能通过不同的路径，传递到响应点。[2][3]

假设某系统受到m个激励力作用，每个激励有x,y,z三个方向分量（用k=1,2,3表示），每个激励分量都对应着n个特定的传递路径，那么这个激励分量和对应的传递路径就产生一个系统响应分量，整个振动响应可以表示为：

Hmnk表示传递函数，Fnk表示激励频谱。

1.3 模态贡献量及响应分析

1.3.1 模态贡献量

模态贡献量是某阶模态的响应在总响应中的比重，模态分解后得到模态贡献量。通过贡献量分析，优化更有方向性，修改某一阶模态而改进总响应。

1.3.2 响应分析

响应分析是以传递函数曲线为响应目标，基于模态贡献量分析，预测曲线优化前后的变化趋势，快速得到优化方向。

2 悬架系统测试与仿真

2.1 悬架系统实验测试

测试采用力锤敲击，采集测点响应，完成数据处理及拟合的方法对其进行测量。主要测试部件包括前下摆臂、前副车架、后扭力梁，示意图如图1所示。

图1 悬架系统零部件模态测试示意图

识别前后悬架振动传递的主要路径及激励方向，布置传感器进行传递函数测试，如图2所示。

图2 传递函数测试点示意图

测试结果用于和仿真分析结果对比，验证有限元模型精度。

2.2 悬架系统仿真分析

建立悬架系统有限元模型，如图3。

图3 悬架系统有限元模型示意图

设置模态分析工况，计算并提取相应结果。传递函数分析边界条件及考察指标与测试保持统一，分析模型如图4所示。

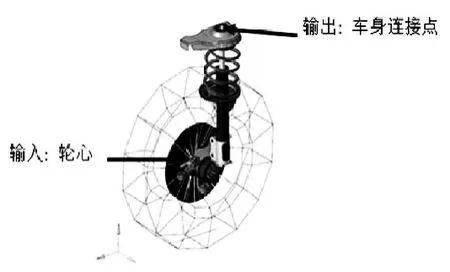
图4 振动传递函数分析示意图

3 验证分析

对比悬架系统零部件模态仿真分析结果与实验测试结果，以及传递函数分析与测试结果，验证有限元模型精度，为后期传递函数分析研究奠定基础。

3.1 零部件精度验证

将实验测试结果与仿真结果进行对比，误差低于 5%，精度满足要求，如表1所示。

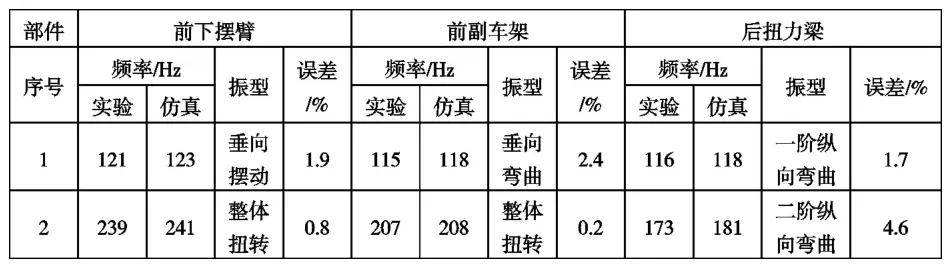
表1 零部件模态精度验证

3.2 传递函数验证

传递函数峰值对应的频率、曲线变化趋势基本一致，精度满足要求，如图5、6所示。

图5 前悬架传递函数验证

图6 后悬架传递函数验证

备注：红色曲线为实验测试结果曲线，黑色曲线为仿真分析结果曲线

综合模态、传递函数验证结果，悬架系统有限元模型可用于进一步研究。

4 传递函数研究

对传递函数曲线某个峰值频率进行模态贡献量分析，精准找出对该处峰值影响较大的模态频率，并进行响应分析，计算该频率对峰值及整个频道段内传递函数的影响[4]。

4.1 模态贡献量分析

以前悬架轮心至前减震器车身安装点振动传递曲线为例，对 43Hz处峰值进行模态贡献量分析，得到传递函数该峰值贡献量较大的前5阶模态，如图7所示：

图7 模态贡献量分析结果示意图

在五个主要贡献的模态频率中，第41阶模态（43.82Hz）和第31阶模态（14.81Hz）贡献量相对较大，分别为+39.36%和+31.87%。

4.2 响应分析

计算第41阶模态在整个频率段对传递函数的影响，所得优化前后传递函数对比如下图8所示；该阶模态对43Hz峰值削减明显，若对其他关注频率点有反作用，则该优化不可取。

图8 传递函数优化前后对比

备注：蓝色实线为优化前传递函数曲线，红色虚线为优化后传递函数，绿色实线为优化百分比。

据上分析结果，第41阶模态对43Hz处响应削弱明显，在整个考察频率范围内，对传递函数有不同程度的优化效果。结合对应的模态振型，对其进行结构优化。从而对传递函数在 43Hz处的峰值进行较大幅度的优化，并且在其他频率点也有不同程度的优化。

另一方面，多条传递路径进行模态贡献量以及响应分析时，在权衡各条路径中模态贡献量的同时，响应分析也要关注多个响应点的变化趋势，如此更有利于我们找到响应优化的最佳方向。

5 总结

结合悬架系统模态实验及传递函数测试，对有限元模型调校及分析，使模型达到精度要求。在精度提升过程中，识别影响悬架系统传递特性的主要因素，并基于有限元分析所得的悬架系统振动传递函数，对曲线峰值频率进行模态贡献量分析，找出影响该峰值的主要模态频率，进行响应分析，快速找到优化前后结果对比及传递函数变化趋势，明确优化方向，提高悬架系统隔振性能。