风向分辨率及零位误差对船舶真风解算误差影响研究

李志乾，宫永翔，漆随平，胡桐，于宏波，王东明

(1.齐鲁工业大学(山东省科学院)，山东省科学院海洋仪器仪表研究所，山东省海洋监测仪器装备技术重点实验室，国家海洋监测设备工程技术研究中心，山东 青岛，266001)

大中型船舶一般都安装有船舶气象仪，为船舶提供实时气象导航，尤其是风速风向等参数在船舶航渡、抛锚和靠泊等过程中有着不可替代的作用，因此，风测量的准确性尤为重要。Iwasaka[1]对自愿观测船舶测量的风速和风向进行了误差估计研究。Moat等[2]研究了船舶形状和风速计安装位置对风速测量的影响。王国峰等[3]通过空间测量的方法确定测量误差与空间倾角的对应关系，提出一种基于空间模型的风速风向测量误差补偿算法，建立了船舶运动状态下风速风向矢量的空间模型。周亦武等[4]通过对大量实验数据的分析，提出了基于多变量非线性拟合的补偿算法，实现了船舶摇摆影响下风速风向的高准确度动态测量。江立军等[5]研究了船舶运动状态下超声波风速风向动态测量建模与分析。郜冶等[6]研究了舰载风速仪测量误差与安装位置的关系，给出了风向角及风速值测量误差随安装位置的变化规律，以及船体本身对风速仪测量精度的影响程度。田东霞等[7]对单体建筑物进行了敏感性试验分析，定量评估了气象站风观测对障碍物的距离要求。郭颜萍等[8]对锚泊状态下未来0.5 h的船面风速和风向进行估算。上述文献研究了传感器实测风的误差控制方法，并取得了一定应用效果。但是，海上航行船舶需要的是真风，真风是指合成风扣除船舶因运动产生的航行风计算出来的自然界实际风，实测风误差并不能如实反映真风误差情况。本文从传感器风向分辨率及船舶真风解算模型的原理出发，分析测风传感器零位安装误差对真风速解算的影响，对传感器在船上的安装有重要的实践指导作用。

1 船舶真风解算误差模型

风既有大小，又有方向，是一种常见矢量。不考虑安装误差时，记传感器实测的相对风为V，船舶因运动而产生的航行风为H，自然界真风为T，风的合成遵守运动合成法则：T=V-H，此即理想情况下船舶真风解算模型。

真风速解算矢量模型转化为标量形式：

‖T‖2=‖H‖2+‖V‖2-2·‖H‖·‖V‖·cosαHV。

(1)

在公式(1)中，αHV是航行风与相对风的夹角，当有零向安装误差时，αHV=α+δ，αHV误差中包含测角误差mα和固定误差δ。

此时的标量形式：‖T‖2=‖H‖2+‖V‖2-2·‖H‖·‖V‖·cos(αHV+δ)，由于是矢量解算，零向误差并不是线性传到真风。考察固定角度误差δ对真风速的计算影响。

2 测风传感器风向分辨率对真风速的影响

风向分辨率是指传感器的风向最小分辨刻度，以某型号测风传感器5°分辨率为例，分析风向分辨率对真风解算的影响。T是自然界真风，与船舶运动无关，可记为常矢量C，航行风H由船舶运动而产生，与航速航向所组成的矢量相同，相对风H是运动合成风，随船舶航速航向的变化而变化。

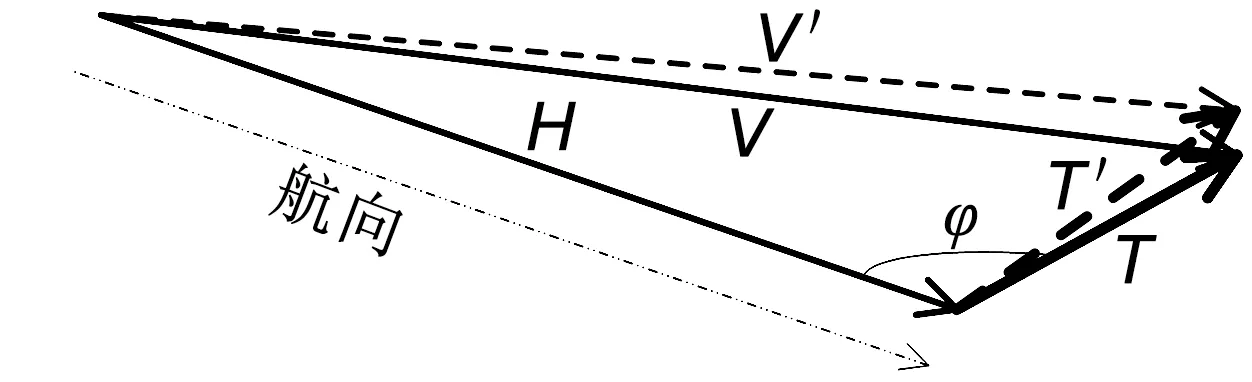
图1 风向分辨率对真风的影响Fig.1 Influence of wind direction resolution to the true wind

图2 风弦角示意图Fig.2 Schematic diagram of wind chord angle

如图1所示，真风为T(常矢量C)，船舶与真风呈φ角度航行，航行风为H(可由航速航向给出)，传感器实测相对风大小为‖V‖，由余弦定理可算得航行风与相对风的夹角

(2)

公式(2)中，由于传感器5°分辨率的限制，相对风向实际读数为β=k·5，此时的相对风应为V′，如图2所示。将相对风V′和航行风H带入真风解算模型，计算得到真风T′，见图1。

在风向分辨率限制下，计算真风速值为‖T′‖，环境真风速值为‖T‖，记

f(Δ) =‖T′‖-‖T‖

(3)

在公式(3)中，航速‖H‖与真风‖T‖一定时，此时f(Δ)的大小与传感器的风向分辨率有关。当航向与真风的夹角φ=130°与φ=150°时，f(Δ)随‖H‖与‖T‖的变化如图3所示，5°风向分辨率对真风解算的影响在±0.5 m/s之间，且航速越小则误差也越小。该现象可结合图1,2解释，当航行风‖H‖增大时，相对风‖V‖也增大，弦角α则相应减小，但由于传感器风向分辨率的限制，弦角α减小量并不明显，造成相对风向理论值与实测值有所偏差。

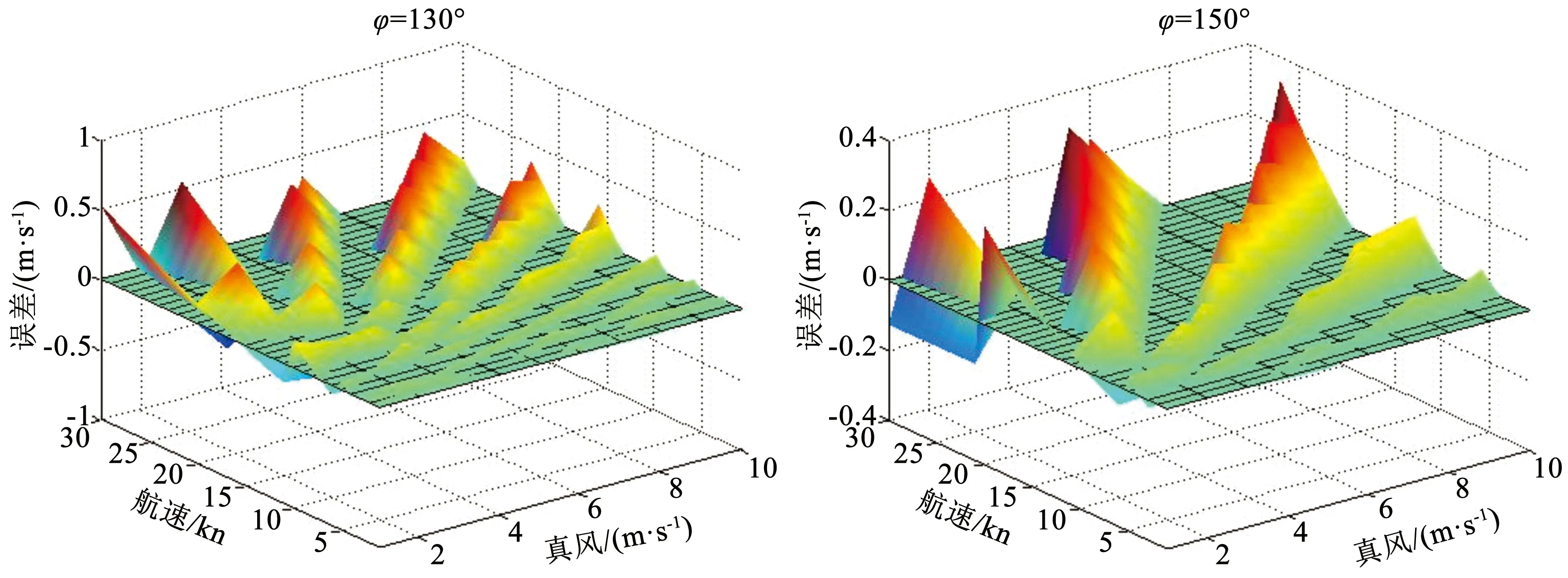
图3 5°风向分辨率对真风解算的影响Fig.3 Influence of 5° wind direction resolution on the true wind

不考虑航行风误差情况下，由图3可知，传感器风向分辨率对真风计算结果的影响与航速大小有关，5°风向分辨率对真风速的影响总体在±0.5 m/s以下。

3 测风传感器零位安装精度对真风速的影响

传感器实测的相对风向是以船艏艉线为参考，来风方向与船艏向的夹角，如果传感器零位安装不准，在真风解算过程中会引进一角度固定误差。因船舶真风解算模型的非线性，其对真风计算结果的影响也是非线性的，无法直接消除。下面推导风向分辨率及安装误差对真风计算的误差模型。

记相对风向读数为α，真风解算模型的标量形式‖T‖2=‖H‖2+‖V‖2-2·‖H‖·‖V‖·cosα中，记风向分辨率产生的误差为δ，零向安装误差为θ，实际真风速应为

(4)

本文分两种情况来分析零位安装误差对真风解算的影响。

3.1 负向零位安装误差

如图4所示，在相对风V、航行风H和真风T组成的矢量三角形中，由余弦定理算得相对风与航向的夹角应为α。在图5中，由于负向零位角θ的存在，传感器的风向读数应为β=α-θ，再加上风向分辨率的叠合影响，传感器的示值应为γ=β+δ。如图4所示，此时的相对风为V′，再将V′带入真风解算模型求得T′，负向零位角引起的真风解算误差为f(Δ)=‖T′‖-‖T‖。

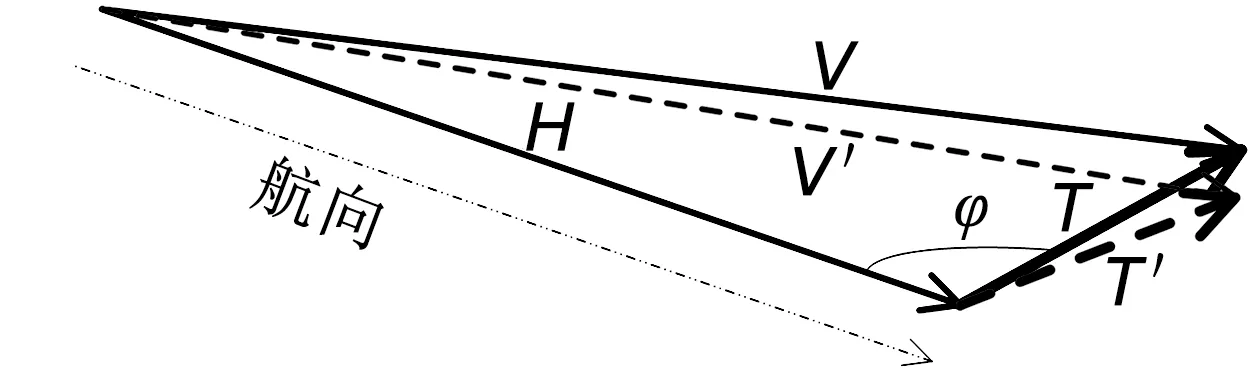
图4 负向零位对真风解算的影响Fig.4 The influence of negative zero position on the calculation of true wind

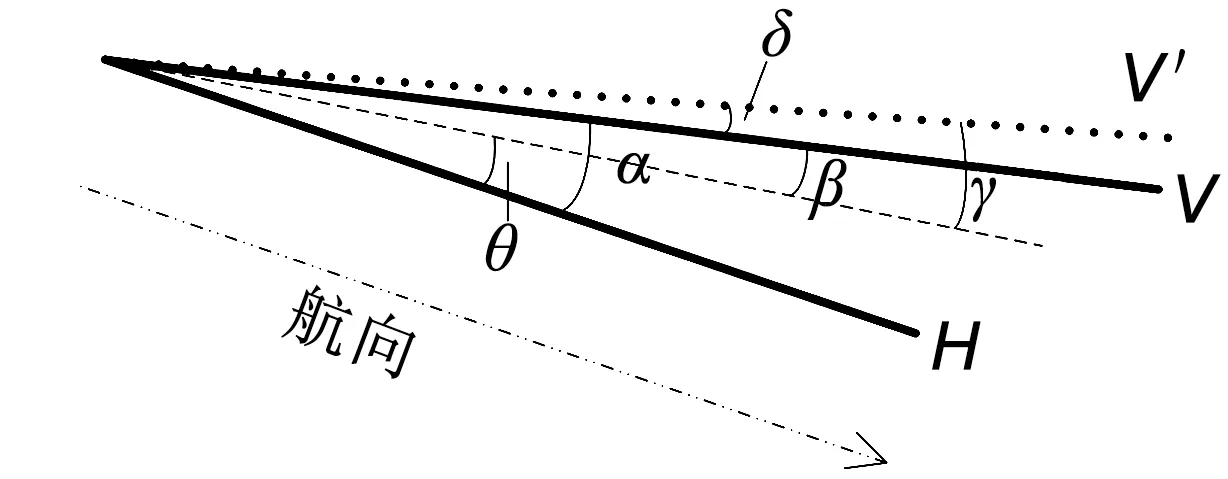
图5 负向零位风弦角示意图Fig.5 Negative zero position wind string angle diagram

令φ=130°，θ=-12°，f(Δ)随‖H‖与‖T‖的变化如图6所示，从图中可以看出，真风误差是负值，说明模型解算出的真风要小于实际真风，航速越大误差也越大，且真风越大误差也越大。

图6 -12°零向安装误差Fig.6 -12° zero direction installation error

3.2 正向零位安装误差

同理，如图7所示，在相对风V、航行风H和真风T组成的矢量三角形中，由余弦定理算得相对风与航向的夹角应为α，在图8中，由于正向零位角θ的存在，传感器的风向读数应为β=α+θ，再加上风向分辨率的叠合影响，传感器的示值应为γ=β+δ，如图7所示，此时的相对风为V′，再将V′带入真风解算模型求得T′，正向零位角引起的真风解算误差为f(Δ)=‖T′‖-‖T‖。

图7 正向零位对真风解算的影响Fig.7 The influence of positive zero position on the calculation of true wind

图8 正向零位风弦角示意图Fig.8 Positive zero position wind chord angle diagram

图9 12°零向安装误差Fig.9 12° zero direction installation error

4 结语

固定平台上的风速风向传感器，其零向安装误差是一个固定误差，可通过与其他测风装置对比来消除；对移动平台来说，如船舶在海上航行时，安装在桅杆上的风速风向传感器实测的是运动合成风，而实际需要的是真风。本文分析了传感器风向分辨率与零位安装误差对船舶真风解算的影响，从分析的结果来看，5°以内的风向分辨率对真风计算的结果影响不大，但叠加传感器的零位安装误差后，尤其是正向误差(如安装误差在11°以上)，在高航速高真风的情况下，能达到30%以上的误差。要提高真风的测算精度，在安装施工时需严格控制传感器零位安装误差。