电力电子电路故障诊断技术探索与预测
倪巧云
(湖北工业大学,湖北武汉430064)
0 引言
在现代电子设备中,电力电子电路的应用非常广泛,且国内外研究人员高度重视对其健康管理的研究,早期研究的内容集中在电力电子电路故障诊断方面。为了及时在电力电子电路故障发生前发现问题,研究人员越来越重视对故障预测的研究,即:依据电路在运行中的退化和趋势,预测其未来的健康水平。下面,笔者主要探讨电力电子电路故障诊断与预测技术。
1 电力电子电路故障诊断
1.1 小波分析
小波是小的波形。小波分析是分析信号的频率与时间的方法,其能在频域、时域上表征信号的局部特征,且其频率窗、时间窗均可改变,即利用平移、伸缩灯运算功能多尺度细化分析信号,以提取出信号中的有用信息。研究发现,小波分析表现出多分辨率分析的特征,即:低频部分的时间分辨率较低,频率分辨率较高;高频部分的时间分辨率较高,频率分辨率较低。其目的是构造在频率上与平方可积的实数空间L2(R)高度逼近的正交小波基,用以发挥不同带宽的带通滤波器的作用。据此特性,可提取出信号中的有用信息,并忽视其中的干扰信号或噪声。
1.2 马氏距离
马氏距离由统计学家P.C.Mahalanobis提出,即指数据的协方差距离,其可有效计算出某一样本与样本集的间隔距离或相似性。马氏距离的性能在模式识别中比欧式距离更优,且量纲不会对其产生影响,即数据单位不会对点间马氏距离产生影响,同时马氏距离考虑进了特性间的联系且从测量尺度中独立开来。研究发现,在马氏距离的计算中,总体样本数n要求比样本维数m大,否则会得到无效的总体样本协方差矩阵逆矩阵,继而使马氏距离计算失败。
1.3 电路故障诊断流程
下面,笔者在电力电子电路软、硬故障诊断中引入小波分析与马氏距离,其中前者用来分析电路信号和提取故障的特征参数;后者用来度量某一电路故障与待测电路的距离和求取待测电路与一切故障类型的马氏距离,且若某一马氏距离出现最小值,则对应故障便为待测电路的故障。图1所示为基于小波分析与马氏距离的电力电子电路故障诊断流程图。
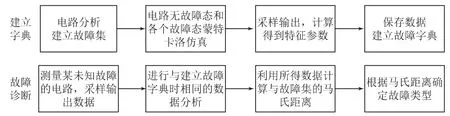
图1 电路故障诊断流程图
图1所示的电力电子电路故障诊断流程图由建立字典、故障诊断组成,即:
(1)建立故障字典:首先,创建Pspice电路文件,并分析软、硬故障可能有的模式,继而建立故障集;其后,对处于故障、健康状态的电路分别开展蒙特卡洛仿真分析,并采样求取测量点对应的电压值;最后,分析数据,并算得某一故障对应的故障特征向量,继而建立故障字典。
(2)故障诊断:首先,通过对待测电路输出电压采样,以获得数据和求取故障特征参数;其后,根据特征与故障字典提供的数据,求取未知故障电路的特征参数与每一故障(故障字典)的马氏距离,并找到与最小马氏距离对应的故障号,即为待测电路故障。
为了检验基于小波分析与马氏距离的电力电子电路故障诊断方法是否有效,可通过反复分析和诊断待测电路的未知故障,以确定诊断结果的准确度和故障诊断的准确率。
2 电力电子电路故障预测
2.1 AR模型预测算法
AR模型(自回归模型)是一类具备连续功率谱的线性时间序列信号模型,其常用在平稳随机序列的研究中。其中,平稳随机序列产生于典型噪声源对线性系统的激励作用,噪声源通常选择白噪声。关于AR模型,可用下列公式表示其差分方程:
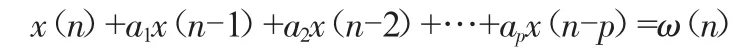
可见,根据x(n)前p个点,可算得x(n)的值及AR模型的参数ai。AR模型参数常用最小二乘法、Burg递推法、列文森法、自相关函数法和Yula-Walker法进行求解。其中,最小二乘法(或最小平方法)是通过最小化误差的平方来寻求数据的最佳函数匹配,其可快速求得未知数据及使其与实际数据的误差平方和最小;Burg递推法是先用格型预测误差滤波器来求取前、后向预测误差的最小平均功率,再运用列文森递推公式计算AR模型系数、输入噪声方差,其中针对AR信号,运用Burg算法可提高估计的精确度。
2.2 BP神经网络预测算法
BP算法是BP神经网络(多层前馈神经网络)在学习中运用的误差逆传播算法,其原理为:先从样本数据与网络输出中获得误差函数,再运用梯度下降法求取误差函数的最小值,然后不断修正神经网络连接权值,以使网络误差在允许范围内。基本的BP算法由信号前向传播、误差反向传播两部分组成,即:网络输出按“输入→输出”的方向进行计算;权值与阈值按“输出→输入”的方向进行修正。其中,在误差反向传播过程中,先对每一层神经元逐层算出输出误差,再逐层运用梯度下降法算出连接权值、阈值,直到整个网络全局的误差满足给定极值的要求,自此可从权值与阈值中获得历史数据与未来值得关系,并用于预测数据。在实际使用中,BP神经网络要求重点考虑期望误差、学习速率、阈值初值、网络权值、隐层神经元数目和输入层个数的选取。
在神经网络中,BP算法被认为是最成熟、使用最多的训练算法。其中,神经网络初值可随机初始化,但其易向局部最小点收敛,则为了克服随机选取的缺点,建议在神经网络初值计算中引入遗传算法,用以增强所得模型的曲线拟合能力。其中,遗传算法的演算步骤为选择→交叉→变异。神经网络初值经遗传算法优化后,可赋予网络,用以训练网络,继而获得网络参数。
2.3 改进预测算法
电力电子电路健康状态衡量值的波动具有非线性、复杂性(亦或混沌特性),故可运用混沌信号分析法来进行数据分析,继而优化电路的预测效果。下文,笔者从混沌时间序列相空间重构理论的角度,探讨AR模型、BP神经网络模型预测效果的优化(图2),即:先按相空间重构理论获得嵌入维数m、时间延迟τ,并相空间重构数据,其后再用AR模型、BP模型训练和预测数据矩阵。
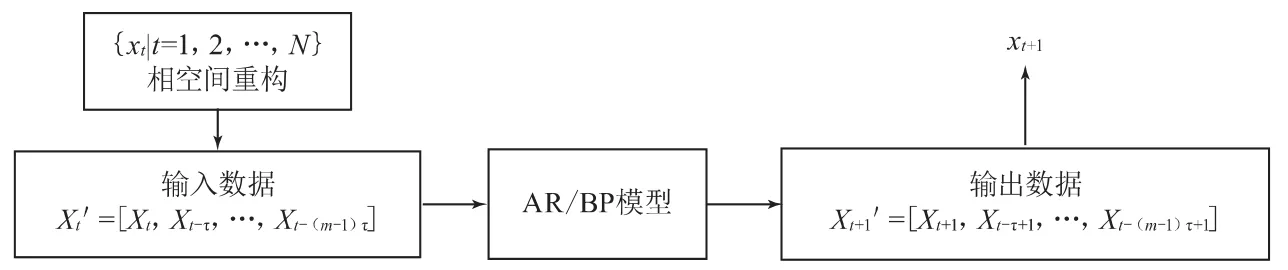
图2 相空间重构后的预测流程
3 结语
综上研究,基于小波分析和马氏距离的电力电子电路故障诊断方法可高效检测参数性、结构性故障,且基本可准确定位故障点。同时,本文谈及的AR模型预测算法、BP神经网络预测算法等方法可有效预测电力电子电路的健康状态和剩余寿命。但针对电力电子电路故障诊断与预测技术的研究仍待完善,值得高度重视。

