基于平均化骨骼模型的接骨板优化设计
张荣丽,何坤金,张玉雪
(1.河海大学 物联网工程学院,江苏 常州 213022; 2.常州市图形图像与骨科植入物数字化技术重点实验室,江苏 常州 213022)(*通信作者电子邮箱kjinhe@163.com)
0 引言
人口老龄化的加剧和各类交通事故的频发导致骨科植入物的需求大幅度增加。目前,外科手术中最常见的骨科植入物有:接骨板、髓内钉、钢针等,其中接骨板的设计是植入物设计的核心[1-2]。接骨板的设计包括个性化设计和系列化设计[3],相较于个性化接骨板,具有通用性的系列化接骨板应用更为广泛。然而,系列化接骨板目前仍存在一些问题。尺寸设计方面,技术水平限制我国现有系列化接骨板主要是参照国外参数生产,骨骼形状的较大差异导致从国外引进的接骨板形状尺寸难以满足国人的需求。其中,在材料和应力方面,接骨板的主要制作材料钛合金价格昂贵,且由于应力集中导致接骨板易断裂。
近年来,数字骨科[4]发展迅速,申晓光等[5]从工程加工角度上总结了快速成型技术在人工假体等制造技术的研究成果,为我国在数字骨科领域奠定了基础;任龙韬等[6]采用CT(Computed Tomography)原始数据实现骨折的模拟复位及个性化解剖型接骨板的三维实体模型的创建;Nrto等[7]从设计的角度先基于骨骼表面生成接骨板的大致形状,并对其进行修剪生成符合患者所需形状模型,实现术前规划。上述研究提出了基于骨骼模型设计个性化接骨板,但设计方法可重用性差。Yumer等[8-9]提出利用语义特征编辑形状,该方法允许非专业用户利用语义引导形状变化,关键问题在于构建高层语义参数与底层几何元素之间的映射关系;Langerak[10]在自由曲面上定义语义参数,基于特征提供对形状的高级控制。上述研究提出了曲面的参数化设计,考虑到接骨板基于曲面设计,可将参数化思想应用于接骨板设计中。Arnone等[11]提出了采用基于有限元分析的计算机辅助仿真模型指导骨科植入物的设计方法;Kaman等[12]提出基于有限元的数值仿真,估算胫骨手术中接骨板和螺钉受到的冯米斯应力;Megan等[13]对锁骨固定接骨板的有限元参数进行研究,指出接骨板的厚度对其结构刚度有较大的影响。上述研究成果提出利用有限元分析接骨板的应力,然而,通过调整厚度参数实现接骨板材料节约以及应力分散的文章鲜有报道。
课题组对平均化骨骼的构建和接骨板设计已有相关研究[14-15],重点研究了平均化语义骨骼模型的构建和接骨板贴合面层次参数化设计。本文在课题组已有研究成果的基础上,着重研究基于平均化几何骨骼模型设计具有一般性的通用接骨板,定义接骨板的实体参数,并对其作优化设计,关键问题在于如何获取平均化骨骼模型以及如何快速有效地优化接骨板厚度。本文通过带权值的平均化骨骼模型,设计指定类型接骨板及定义语义参数,以便于后期接骨板的优化修改;并利用二分策略快速修改接骨板厚度参数,在满足应力的条件下尽可能减少材料。
1 平均化骨骼模型生成
接骨板的设计依赖于骨骼模型特征[16],平均化骨骼模型为系列化接骨板数量及其尺寸大小的合理分布提供了科学依据。本文构建了带权值的平均化骨骼模型生成方法,如式(1)所示:

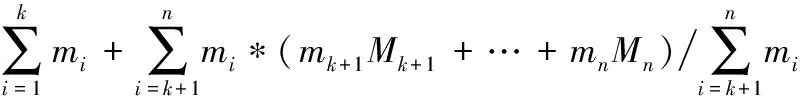
(1)
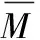
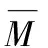
(2)
构建平均化骨骼模型包括如下步骤:
步骤1 将N个同类型的骨骼点云或者网格模型看成N个节点的集合,且每个节点设有权值。
步骤2 选出节点集合中任意两个节点(如图1(a)~(c)),利用刚体配准和非刚体变形[17](如图1(d)、(e)),使两个骨骼具相同的拓扑结构(如图1(f)),生成一个新的平均化节点(如图1(g)),其权值为选出的两个节点的权值之和。
步骤3 从节点集合中删除选取的两个节点,将生成的新的平均化节点加入到集合中。
步骤4 重复步骤2,直到集合中最后一个节点,即为平均化骨骼模型,权值为N个节点的权值之和。
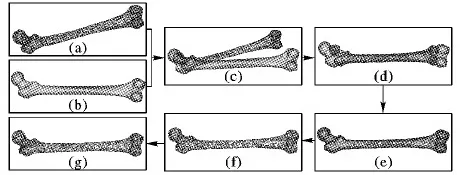
图1 任意两根骨骼配准变形获取平均化模型
以股骨为例,采集100根形状尺寸各不相同的股骨作为节点集合。首先,定义初始状态下股骨的权值为1;其次,选取其中任意两根股骨(一根作为源模型,一根作为目标模型),通过刚体配准和非刚体变形生成一个新的平均化模型,其权值为2;然后,在100根股骨模型集中删除选取的两个股骨模型,将新生成的平均化股骨模型加入到模型集中;最后重复以上步骤,直至最后一根股骨,此时其权值为100,该骨骼即为100根股骨的平均化股骨模型。
2 基于平均化骨骼模型的接骨板设计
基于平均化骨骼模型可以设计出具有一般性的通用接骨板,以股骨三叶型接骨板为例,具体设计方法如下:首先,在平均化股骨模型表面定义感兴趣区域并绘制边界线,如图2(a)、(b)所示;然后,定义感兴趣区域内部约束线,如图2(c)所示;最后,通过曲面生成方式(如填充)生成新的独立曲面,该曲面即为接骨板的贴合面,如图2(d)所示。
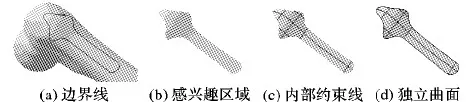
图2 选取感兴趣区域构建接骨板贴合面
为实现接骨板形状的修改和编辑,需要作贴合面参数化设计,重点在于如何通过修改少量的语义参数实现接骨板贴合面变形。接骨板贴合面为自由曲面,其参数化定义较为复杂,本文采用基于特征点和特征线的层次化参数化方法[18-19]:底层参数描述曲线和曲面的特征点,如图3(a)所示;中间层参数描述特征线形状,包括边界线和内部约束线,如图3(b)所示;高层语义参数用于描述曲面形状,如图3(c)所示。各层参数之间存在约束关系[20-21],通过少量高层语义参数实现曲面特征的修改。
贴合面参数用于描述曲面形状,实体参数用于定义接骨板不同位置的厚度,实体参数是本文的重点。厚度参数定义在接骨板贴合面和外表面之间,生成贴合面之后,运用式(3)生成外表面:
E(u,v)=A(u,v)+d(u,v)*I(u,v)
(3)
其中:A(u,v)是贴合面;E(u,v)是外表面;d(u,v)是贴合面与外表面不同位置的厚度;I(u,v)是贴合面不同位置的单位法向量。外表面相应关键点的位置可以式(4)表示:
Pi′=Pi+di*Ii
(4)
其中:Pi′是外表面对应的关键点,Pi是定义在贴合面上的关键点,di是厚度参数,Ii是Pi位置的单位法向量。
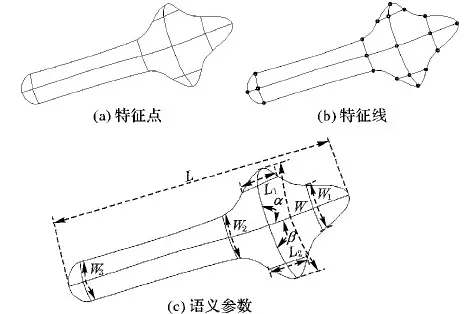
图3 接骨板贴合面参数化
结合式(3)和式(4),构建接骨板主要包括以下步骤:
步骤1 选取感兴趣区域构建接骨板贴合面,如图4(a)所示;
步骤2 在贴合面上定义关键点、约束线和语义参数,建立各层参数之间的约束关系,通过调整语义参数编辑修改贴合面,如图4(c)、(d)所示;
步骤3 在贴合面关键点定义厚度参数生成对应的外表面关键点,如图4(e)所示;
步骤4 基于步骤3生成的关键点构建外表面,并定义厚度语义参数,如图4(f)所示;
步骤5 连接贴合面和外表面生成接骨板实体,如图4(b)所示。
3 接骨板优化
在参数化接骨板的基础上,通过修改语义参数,可以快速设计出形状尺寸各不相同的系列化接骨板。针对接骨板的优化,本文在选择尺寸大小适合的接骨板基础上,侧重于厚度参数的修改作接骨板优化,以减少接骨板材料使用,分散接骨板应力。
3.1 接骨板变形与分析
在接骨板不同位置定义不同厚度参数值,其应力强度也不同。针对上文中在平均化股骨模型上设计的三叶型接骨板,在其关键位置定义5个厚度参数H1、H2、H3、H4、H5,如图5所示。通过修改厚度参数值可以生成新的接骨板,如图6所示。
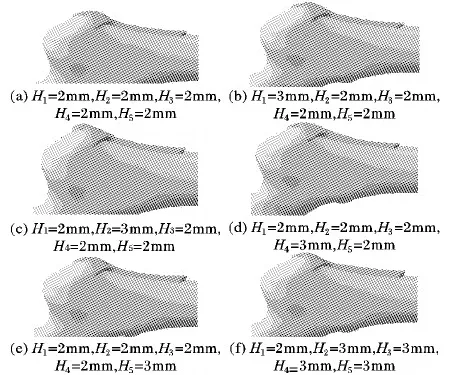
图6 不同厚度接骨板
接骨板在人体内受到的载荷受到各种因素的影响,包括肌肉、韧带与螺钉摩擦力以及冲击载荷等[22]。本文仅考虑正常60 kg成年男子单腿站立时接骨板受到的轴向压缩力,其余影响因素忽略不计。接骨板所受轴向压缩力的载荷设定为600 N,方向设定为与板面平行线呈15°角,与人直立时的负重力线一致[23]。接骨板材料为医用钛合金,弹性模量为105 GPa,泊松比为0.3。对上述不同厚度接骨板作有限元分析得出应力分布图,如图7所示。实验结果显示不同厚度接骨板所受应力也不同。为了快速合理地设计出满足应力需求的接骨板,在3.2节提出了优化方法。

图7 不同厚度接骨板应力分析
3.2 接骨板优化
制造接骨板的材料通常有两种:钛合金和不锈钢。钛合金由于其具有质量轻、高强度和高韧性的特点在接骨板制造中被广为使用;但是钛合金价格昂贵,而且由于应力集中导致接骨板易断裂,因此,为了减少质量节省材料,同时使应力尽可能分散,需要对接骨板作优化设计。Andrade等[24]和Kutuk等[25]提出一种基于拓扑优化获取接骨板最小质量的方法;Arnone等[11,26]提出一种基于计算机辅助工程减少植入物质量使其满足安全系数约束的设计方法。然而,以上方法均基于相同厚度的接骨板设计。本文提出在贴合面固定在受损骨骼的前提上优化接骨板厚度,对接骨板作不等厚设计,在应力集中的位置增加厚度;相反则减少厚度。
式(5)给出了计算接骨板体积的微积分方程:
M=∬d(u,v)dσ=∬|E(u,v)-A(u,v)|dσ≈
∑Δs*di
(5)
其中:M是接骨板的体积;Δs是接骨板贴合面的微分面积;di是不同位置的厚度;A(u,v)是贴合面;E(u,v)是外表面,如图8所示。M约等于∑Δs*di。
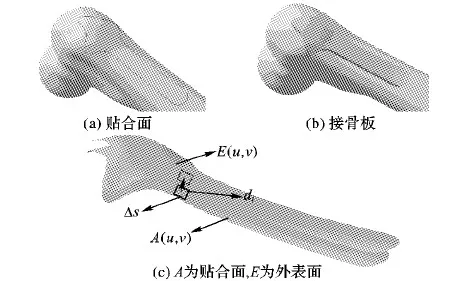
图8 计算接骨板体积
本文采用二分策略快速计算和优化接骨板的厚度,二分策略即基于二分思想有针对性地将大规模数据分解成小的数据集,逐步缩小求解规模。优化流程如图9所示,图中Pi表示接骨板最大压力值,di表示接骨板各个关键位置的厚度,考虑到生产工艺的难度,其数值精确到小数点后两位,dmin表示接骨板最小厚度。
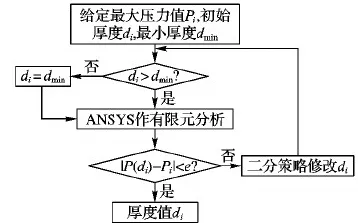
图9 优化接骨板厚度流程
二分策略修改di主要包括如下步骤:
步骤1 首次分析应力后,ti=di,若P(ti)
步骤2 再次分析应力后,若(P(di)-P(ti))*(P(ti)-Pi)>0,则重复步骤1;否则di=(di+ti)/2。
步骤3 重复应力分析,直至满足条件,输出di。
以三叶型接骨板为例,最大压力值Pi设定为医用钛合金的最大屈服强度817 MPa[27],初始厚度值di设定为2 mm,为保证后期接骨板螺钉的固定最小厚度值dmin设定为1.5 mm。具体优化过程如图10所示,步骤中显示了优化过程中不同厚度接骨板的线框图和应力分布图:设定接骨板初始厚度值为2 mm,分析其应力分布情况;然后在应力较小的位置减小厚度参数,在应力较大的位置增大厚度参数,再次进行应力分析;接着利用二分策略迭代,如图10(a)~(c)所示,最终得到满足应力条件下使用材料最少的接骨板,如图10(d)所示。由于钛合金为各向同性的弹性材料,只有一个点或者较小的范围内出现高应力不会对材料整体造成屈服影响,故本文中当接骨板较大范围内应力低于屈服强度时认为满足应力条件。
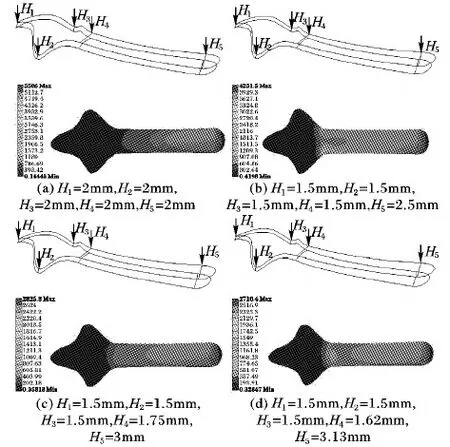
图10 采用二分策略的三叶型接骨板厚度优化过程
3.3 实例分析
对本文所提方法在VC++ 2008和几何造型引擎CATIA V5R21平台进行了实例测试,系统运行环境所需软硬件环境如下:操作系统Windows 7及以上,内存2 GB或以上,CPU 2.1 GHz或以上,硬盘100 GB或以上。最终实现了基于平均化骨骼模型的接骨板优化设计。
以股骨远端Ⅲ型接骨板为例,首先在平均化股骨上选择感兴趣区域构建接骨板贴合面,并对其参数化,如图11(a)所示;贴合面参数化针对接骨板形状设计,修改贴合面参数可以构建大小尺寸各不相同的接骨板,如图11(b)所示;然后在关键点设置厚度参数H1、H2、H3、H4和H5,如图11(c)所示;厚度参数用于描述接骨板不同位置的厚度,如图11(d)~(h)所示;最后通过二分策略和有限元分析优化厚度,图12显示利用该方法优化接骨板厚度的过程,显示了各个步骤不同厚度的接骨板及其应力分布。
在接骨板优化分析过程中:图12(a)接骨板初始厚度设定为H1=2 mm,H2=2 mm,H3=2 mm,H4=2 mm,H5=2 mm,有限元分析结果显示H1、H2应力较大,需增大厚度,H3、H4和H5应力较小,需减小厚度。根据二分策略,修改接骨板厚度值为H1=2.5 mm,H2=2.5 mm,H3=1.5 mm,H4=1.5 mm,H5=1.5 mm,如图12(b)所示;迭代有限元分析和修改接骨板厚度的过程,如图12(c)、(d);最终得出接骨板的最优厚度H1=2.13 mm,H2=2.63 mm,H3=1.88 mm,H4=1.5 mm,H5=1.5 mm,如图12(e)所示,此时接骨板应力较为分散。
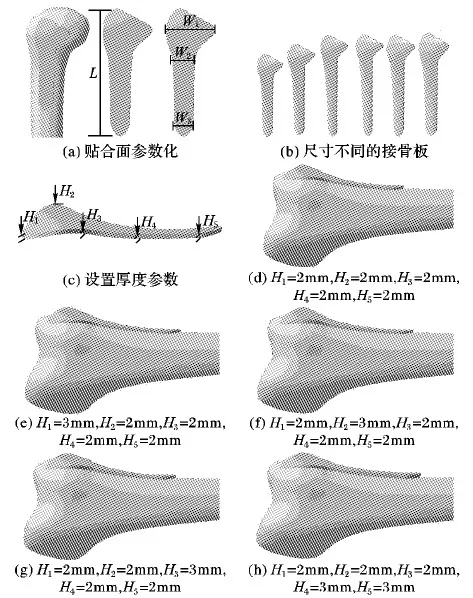
图11 Ⅲ型接骨板的参数化与不同厚度接骨板
将本文中优化前等厚接骨板与优化后不等厚接骨板作体积和最大应力比较,结果如表1所示。由表1可知:三叶型接骨板优化后体积减小2.7%,最大应力减小56.9%;股骨远端Ⅲ型接骨板体积减小12.2%,最大应力减小24.4%。实验表明:利用本文方法优化接骨板可以减少接骨板体积,达到节省材料减小质量的目的;同时优化后的接骨板应力分布更为均匀,降低了接骨板断裂风险。
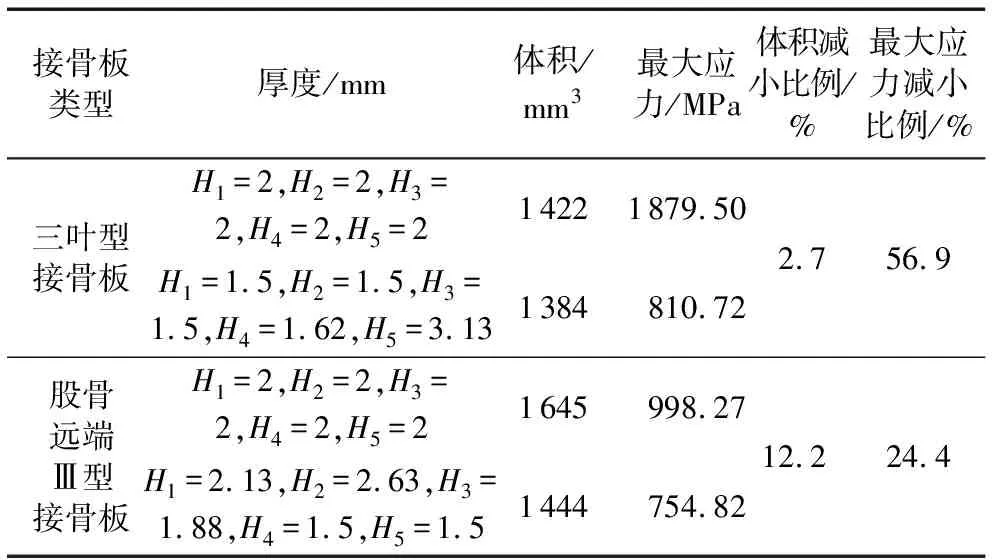
表1 不同厚度接骨板体积与最大应力比较
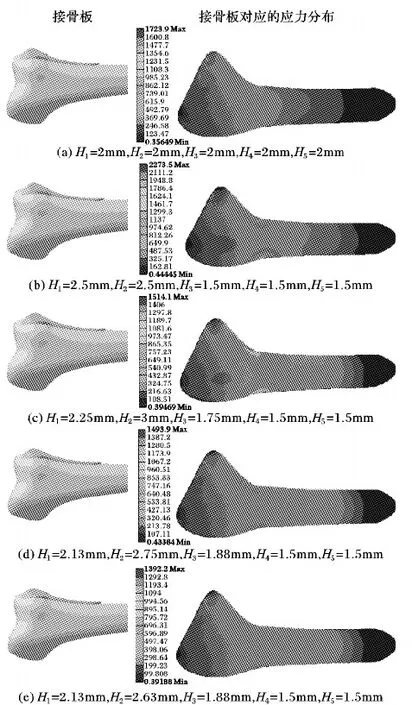
图12 修改厚度参数优化股骨远端Ⅲ型接骨板
4 结语
为优化接骨板应力分布、节省生产材料,本文提出基于平均化骨骼模型的接骨板优化设计方法。主要包括:通过多个同类型骨骼模型,构建平均化骨骼模型;在平均化骨骼模型的指定区域设计接骨板,并定义语义参数;通过二分策略快速修改接骨板厚度参数,使得接骨板在满足应力的条件下使用材料最少。本文方法的特点在于:1)构建了带权值的平均化骨骼模型生成方法,此方法有利于后期的平均化模型扩展,如有新的骨骼模型加入;2)在接骨板上定义语义参数,便于从高层参数编辑修改生成新的接骨板;3)将二分策略应用于接骨板设计优化中,快速构建出理想的接骨板,以满足材料节约和应力分散的要求。下一步工作将结合医学需求,分析统计参数间的关联关系,更好地设计出不同个体需求的个性化接骨板,并进一步优化接骨板的拓扑结构。

