软件众包任务发布优先级计算方法
赵焜松,余敦辉,2,张万山,2
(1.湖北大学 计算机与信息工程学院,武汉 430062; 2.湖北省教育信息化工程技术中心,武汉 430062)(*通信作者电子邮箱yumhy@163.com)
0 引言
随着互联网技术的迅速发展,众包(crowdsourcing)[1]受到了更多工业和学术界人士的极大关注。众包平台,尤其是软件众包(software crowdsourcing)平台,成为当前软件开发的流行方式之一。软件众包的相关研究已成为当前的研究热点之一,众多研究人员就软件众包任务设计、任务标价、欺诈者分析、任务分配、众包工人选择等问题展开了大量的研究。
文献[2-3]中概括了任务分配中相关研究,为以后的研究提供了参考。文献[4]中提出了质量控制策略和众包结果质量评估方法,有效地控制了任务完成质量;但对任务复杂度和效益等考虑不足。文献[5]中对软件任务参与度的影响因素进行了分析,但忽略了发布者对任务的影响。文献[6-7]中对众包质量进行评估,但欠缺对任务发布者的考虑。文献[8]中提出了一种基于用户信誉值的激励机制,并通过仿真实验验证了激励机制的有效性,但涉及实际用户参与度对众包质量的影响。文献[9]中针对众包系统中的激励和信誉机制进行研究,设计了激励机制和信誉机制来确保用户尽最大努力高质量地完成任务,但实际上发布者、众包工作者和众包任务的特征均会对任务发布之后的结果产生一定影响。文献[10]中提出了基于用户可靠性的众包系统任务分配机制,通过仿真实验证明了所设计任务分配机制的高效性;但是活跃度也会对用户有实际影响。文献[11]中提出基于活跃度的众包工作者信誉模型,综合考虑了众包活跃度与信誉值;但并未考虑众包任务本身的特性。文献[12]中针对任务本身的特性,分析了众包任务设计对众包参与者行为的影响;但忽略了任务发布者所产生的影响。然而上述研究并未将任务发布者与任务综合考虑,且都建立在众包任务被分配的基础上。
对于软件众包平台而言,不同的发布者在平台发布软件众包任务的踊跃程度不一样,历史发布任务的总金额不同,因此,不同任务发布者对于平台的重要性是不同的;同时,某个被发布的软件众包任务的效益权重和紧迫程度也存在差异。所以,相对于平台而言,对于不同发布者发布的任务,如何进行优先级排序,从而提高平台收益,是其关注的重点。
本文工作主要研究如何根据发布者和任务的特征,衡量任务发布的优先级。为了解决上述问题,本文假设某时间段内有平台收到若干软件众包任务申请,以优化任务发布次序为目标,提出了一种基于发布者活跃度与任务权重的软件众包任务发布优先级(Task Release Priority, TRP)计算算法:首先,基于任务发布者的活跃度及其任务累积成交额,利用半正弦曲线的时间权重函数度量任务发布者权重;然后,对任务本身的特性进行分析,以模块复杂度、设计复杂度和数据复杂度三个方面度量任务复杂度,衡量任务效益和任务紧急程度,计算得到任务权重;最后,综合考虑发布者权重与任务权重计算得到任务优先数。使用该模型可以使平台以最优的方式确定任务分配优先级,以便合理安排将要发布的任务,最终提高平台收益。
1 软件众包任务发布者权重模型
软件众包任务发布者本身的属性会影响平台收益。为了反映在某一周期内任务发布者对平台的重要程度,本文采用了一种半正弦的时间权重函数作为拟合曲线,通过给不同的任务发布者属性赋予权值来反映其所占比重。
1.1 基于半正弦曲线的时间权重函数
本文约定半正弦曲线函数的时间权重函数为:
weight(t)=[sin (πt/T)+1]/2
(1)
如图1所示,t是距离周期起始时刻的时间,t越小说明距离周期起始时刻越近,即距离当前时刻越远,平台无需对其过分关注,因此所占权重趋向于0;t越大则说明距离当前时刻越近,该发布者对平台的重要程度越高,因此,平台加大其权重。
式(1)中T表示一个具有调节作用的函数周期,不同的t会产生不同权重值结果,t的取值范围为[0,T/2],weight(t)的取值范围在[0,1],适用于反映任务发布者对平台的重要程度。

图1 半正弦曲线
1.2 软件众包任务发布者权重模型
软件众包任务发布优先级模型设计的主要目标之一就是对任务发布者的权重进行计算,以确定该发布者对平台的重要程度。为此,本文定义发布者活跃度Pw和任务累计成交额Vw对发布者权重进行度量。
定义1 发布者活跃度。描述当前任务发布者活跃程度所占比重,以任务发布者在某一周期T内发布任务的次数S度量任务发布者的活跃度,用Pw表示:
(2)
其中:S是周期T内该发布者发布任务总次数,ti表示距离周期起始时刻的时间,ti越大表示该任务距离当前时间越近,说明该发布者对平台重要程度越高,所以其权重越大。
定义2 任务累计成交额。描述该发布者发布众包任务累积成交金额,以任务发布者在某一周期T内累积发布任务的总额来衡量该发布者对平台的重要程度,用Vw表示:
(3)
其中:S是周期T内该发布者发布任务总次数,mi是该发布者发布的第i个众包任务的成交金额,ti表示距离周期起始时刻的时间,ti越大表示该任务距离当前时间越近,说明该发布者对平台重要程度越高,所以其权重越大。
综上,任务发布者权重Wpro计算如式(4)所示:
Wpro=ωPw+(1-ω)Vw
(4)
其中ω为任务发布者权重因子,ω∈[0,1]。实验表明,当ω=0.4时效果最佳。
2 基于复杂度的软件众包任务权重
软件众包任务发布优先级计算中的任务权重模型,是从模块复杂度、设计复杂度和任务复杂度等方面度量任务复杂度,并基于任务复杂度,从任务效益和任务紧急程度两方面计算得到任务权重。对于平台在某时间段接收的任务,用集合T={t1,t2,…,tn}表示,对于每个任务ti∈T,由于任务复杂度、报价、任务期限都存在差异,因此所占权重也不同。
2.1 软件众包任务复杂度计算
任务权重模型中的任务复杂度,是基于软件工程中的软件架构及数据流图模型,并参照文献[13]所述复杂度计算方法计算而来,包括模块复杂度、设计复杂度及数据复杂度三个方面。
模块复杂度Cmod是通过计算系统中各个子模块的复杂度得出,计算如下:
(5)
其中:n表示模块的总数,ev(Gi)表示第i个子模块的复杂度。
设计复杂度Cdes则以系统级模块之间的相互调用关系来度量,其值为程序中所有模块设计复杂度之和,公式如下:
(6)
(7)
其中:Ci, j表示模块i是否调用模块j,若调用,则Ci, j=1;反之Ci, j=0,n是模块总数。
数据复杂度Cstr是使用数据流图中路径个数和每条路径的长度来进行度量,其值为所有路径复杂程度之和。所谓路径,是指从某个特定的输入,经过一系列处理,最终得到某个输出的全流程。数据复杂度计算如下:
(8)
其中:m是数据流图中的路径个数,Lk是第k条路径的长度。
综上,可得任务复杂度Ctas如式(9):
Ctas=αCmod+βCdes+γCstr;1>α>β>γ>0,
α+β+γ=1
(9)
式(9)表明,在众包平台中,模块复杂度是衡量任务复杂度最重要的指标,其次是模块间的耦合程度,而数据复杂性则较为次要。实验表明,当α=0.5,β=0.3,γ=0.2时效果最佳。
2.2 基于复杂度的软件众包任务权重
考虑到报价与完成周期对任务的影响,根据任务复杂度,以单位报价与任务期限度量任务权重。为此,本文定义任务效益和任务紧急程度两个因子来进行任务权重的计算。
2.2.1 任务效益
相对于众包平台,任务报价是其较为优先考虑的因素,本文以任务复杂度与任务报价度量任务效益。当任务复杂度相同时,任务报价越高,任务效益越高。任务效益因子B是将任务复杂度除以任务报价,并将所得结果归一化得来,公式如下:
B=e-Ctas/Q
(10)
其中:Q表示任务的总报价,Ctas表示任务复杂度。
2.2.2 任务紧急程度
为使平台中所有发布者的任务尽可能多地被分配出去,当任务复杂度相同时,任务期限越短,任务紧急程度越高,因此,任务紧急程度因子U是将任务期限除以任务复杂度,并将所得结果归一化得来,公式如下:
U=e-AT/Ctas
(11)
其中:AT表示任务期限,Ctas表示任务复杂度。
2.2.3 任务权重
如上所述,本文定义任务权重Wtas,并采用对数Logistic模式,计算如下:
Wtas=1/(1+e-λB-μU);1>λ>μ>0,λ+μ=1
(12)
其中λ是任务效益权重因子,约束条件1>λ>μ>0表明报价始终是平台优先考虑的因素,因此其所占比重最大,而对任务期限考虑则相对较小,这符合实际中平台的考虑方式。实验表明,当λ=0.8,μ=0.2时效果最佳。
3 软件众包任务发布优先级计算
3.1 软件众包任务发布优先级计算
任务发布优先级模型通过计算任务发布者权重Wpro和任务权重Wtas,得到任务优先数δ,根据任务优先数确定任务发布的优先级。任务优先数δ如式(13)所示:
δ=φWpro+(1-φ)Wtas
(13)
其中φ是任务优先数因子,φ∈[0,1],实际应用表明,当φ=0.6时效果最佳。
任务发布优先级TRP算法描述如算法1所示。
算法1 TRP算法。
输入:任务发布次数S,历史任务总额M,任务报价Q,任务期限AT。
输出:任务优先数δ。
1)基于权重时间函数计算发布者活跃度Pw和任务累计成交额Vw;
2)基于Pw和Vw计算任务发布者权重Wpro;
3)基于系统架构图、数据流图计算模块复杂度Cmod、设计复杂度Cdes和数据复杂度Cstr;
4)基于Cmod、Cdes和Cstr计算任务复杂度Ctas;
5)基于任务复杂度Ctas和任务报价Q计算任务效益因子B;
6)基于任务复杂度Ctas和任务期限AT计算任务紧急程度因子U;
7)基于B和U计算任务权重Wtas;
8)基于任务发布者权重Wpro和任务权重Wtas计算任务优先数δ;
9)返回任务优先数δ,算法结束。
根据以上算法,可以计算出任务优先数,平台根据任务优先数合理安排任务。
3.2 算法复杂度分析
TRP算法主要由三大部分构成,其中,众包任务发布者权重模型中,计算发布者活跃度与任务累计成交额的复杂度均为Ο(n1),所以计算发布者权重的时间复杂度为Ο(n1);在任务权重模型中,计算模块复杂度和数据复杂度的时间复杂度均为Ο(n2),而设计复杂度仅与模块间的相互调用有关,因为有n个模块,所以其时间复杂度为Ο(n22),因此计算任务权重的复杂度为Ο(n22)。综上可知,TRP算法的复杂度为Ο(n1)+Ο(n22)。
4 实验结果与分析
本文提出的软件众包任务发布优先级模型,综合考虑了任务发布者与任务本身的权重,实现了任务发布优先级的排序,其合理性和有效性通过实验予以验证。
4.1 实验数据集
为了验证TRP算法的有效性,本文抓取了程序员客栈上12 739个任务发布者及其成功发布的4 721条任务信息进行实验,由于主要验证不同数据量对算法性能的影响,所以取式(4)中ω=0.4,式(9)中α=0.5,β=0.3,γ=0.2,式(12)中λ=0.8,μ=0.2,式(13)中φ=0.6,任务数量的取值范围是[400,3 600],任务发布者数量的取值范围是[1 000,9 000]。
4.2 实验结果与分析
4.2.1 发布者数量变化对算法的影响
当任务发布者数量为{1 000,2 000,…,9 000}时,分别分析算法准确度和算法运行时间,部分任务发布者信息如表1所示。

表1 任务发布者信息表
当任务数量恒定时,任务发布者数量对算法的影响如图2~3所示。
由图2~3可以看出,当任务数量恒定时,随着任务发布者数量的增加,算法准确度逐渐提升。当任务发布者数量超过7 000之后,算法准确度慢慢趋向于稳定,并基本稳定在0.92。算法运行时间也随着任务发布者数量的增加而缓慢增加,当任务发布者数量超过5 000之后,算法运行时间增大的幅度越来越小,说明数据量太大时,不会对算法的性能造成很大影响,验证了算法的稳定性。

图2 任务发布者数量与准确度之间的关系

图3 任务发布者数量与运行时间之间的关系
4.2.2 任务数量变化对算法的影响
当任务数量为{400,800,1 200,…,3 600}时,分别分析算法准确度和算法运行时间,部分任务信息如表2所示。
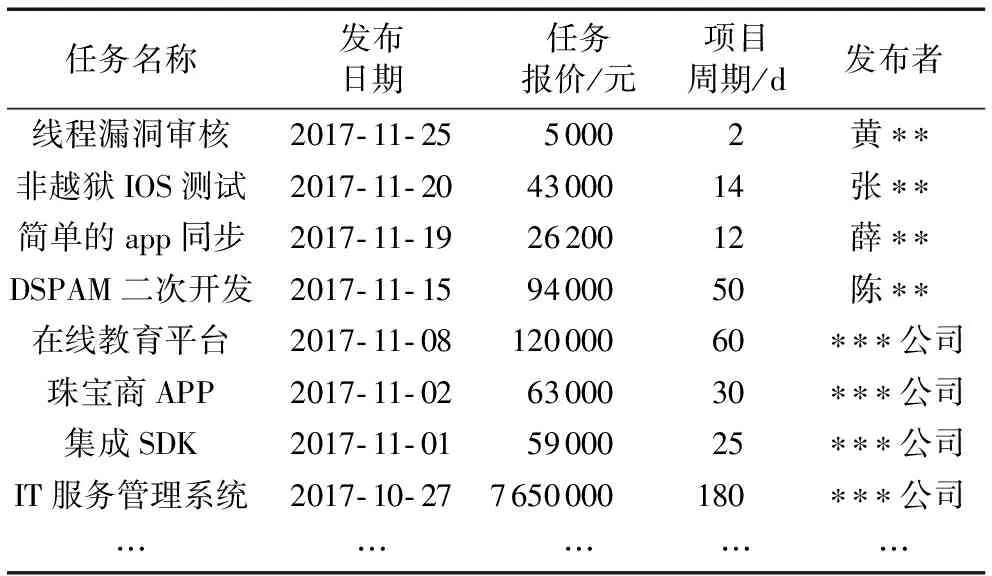
表2 部分任务信息表
当任务发布者数量恒定时,任务数量对算法的影响如图4~5所示。

图5 任务数与运行时间之间的关系
由图4~5可以看出,当任务发布者数量恒定时:随着任务数量的增加,算法准确度逐渐提升,当任务数量超过2 000之后,算法准确度基本稳定在0.93;当任务数量较少时,算法运行时间变化较大,随着任务数量的增加,算法运行时间也缓慢增加;当任务数量超过2 000之后,算法运行时间变化越来越小,基本趋向于水平。由此,验证了算法的有效性。
4.2.3 参数设定
本文利用爬取的数据,在自己的平台上做模拟实验,以确定最适合的参数。每次都选择发布序列中的前100个任务进行实验。
1)任务发布者权重因子ω,任务权重计算中任务效益权重因子λ及任务优先数因子φ的确定。
本文对任务发布前和任务实际接收后的数据进行对比,以任务成功分配的概率作为度量条件,其结果如图6~8所示。

图6 任务发布者权重因子与任务成功分配率之间的关系
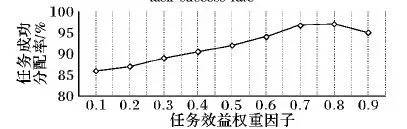
图7 任务效益权重因子与任务成功分配率之间的关系

图8 任务优先数因子与任务成功分配率之间的关系
由图6可知,当任务发布者权重因子ω=0.4时,任务成功分配率最高,为97%;由图7可知,当任务效益权重因子λ=0.8时,任务成功分配率高达97.6%,由式(12)的约束公式可知,此时μ=0.2;由图8可知,当任务优先数因子φ=0.6时,任务成功分配率最高,为98.1%。
2)任务复杂度计算中相关参数的确定。
本文对任务发布前和任务实际接收后的数据进行对比,提出预期复杂可信度,即以任务预期复杂度与软件开发实际复杂度之间的吻合度的高低作为其度量条件,由式(9)可知,α∈[0.4,0.8],γ∈[0.1,0.3],其结果如图9所示。

图9 参数α、γ与预期复杂可信度之间的关系
由图9可知,当参数α=0.5,γ=0.2时,吻合度最高,为98%,此时β=0.3。
5 结语
软件众包任务发布优先级是众包研究中一个重要的环节,本文针对软件众包任务发布过程中发布者和众包任务两大类因素对众包任务优先级的影响,提出了种基于发布者权重与任务权重的软件众包任务发布优先级计算方法。实验表明,该算法具有一定的有效性和合理性,同时也具有较高的稳定性。

