平头弹飞行阻力工程模型*
刘铁磊,沈培辉,梁化鹏
(南京理工大学智能弹药技术国防重点学科实验室,南京 210094)
0 引言
为了提高弹丸的停止作用,实现低侵彻目的,弹丸的弹头形状被设计成平头[1]。该型枪弹较以前枪弹而言,为全新的结构,对其外弹道特性研究较少,尤其体现在缺乏合适的弹丸阻力模型。对于该弹型的外弹道计算与实验数据表明现有的卵形弹和锥头弹阻力模型[2]均不能较好的计算其阻力系数。其主要原因为该弹丸头部形状为平头,弹头激波产生部位与卵形弹和锥头弹的不同,导致弹丸的头部阻力系数发生变化。传统上,计算阻力系数一般通过1943年阻力定律和弹形系数的方法[3]求解,然而该方法不适合正在设计过程中的弹丸;近年来,利用CFD软件进行仿真计算阻力系数得到广泛应用[4],然而该方法联合外弹道方程计算耗时长,且易受建模本身影响。因此,从空气动力学出发,建立平头弹阻力模型用于外弹道计算,并通过实验进行验证与修正,仍然不失为一个好的方法。
1 平头弹激波阻力系数工程模型
对于任意一种锥形平头弹,其形状主要由三个因素确定:前端面半径R1,弹丸半径R2,半顶角a。其外形如图1所示。
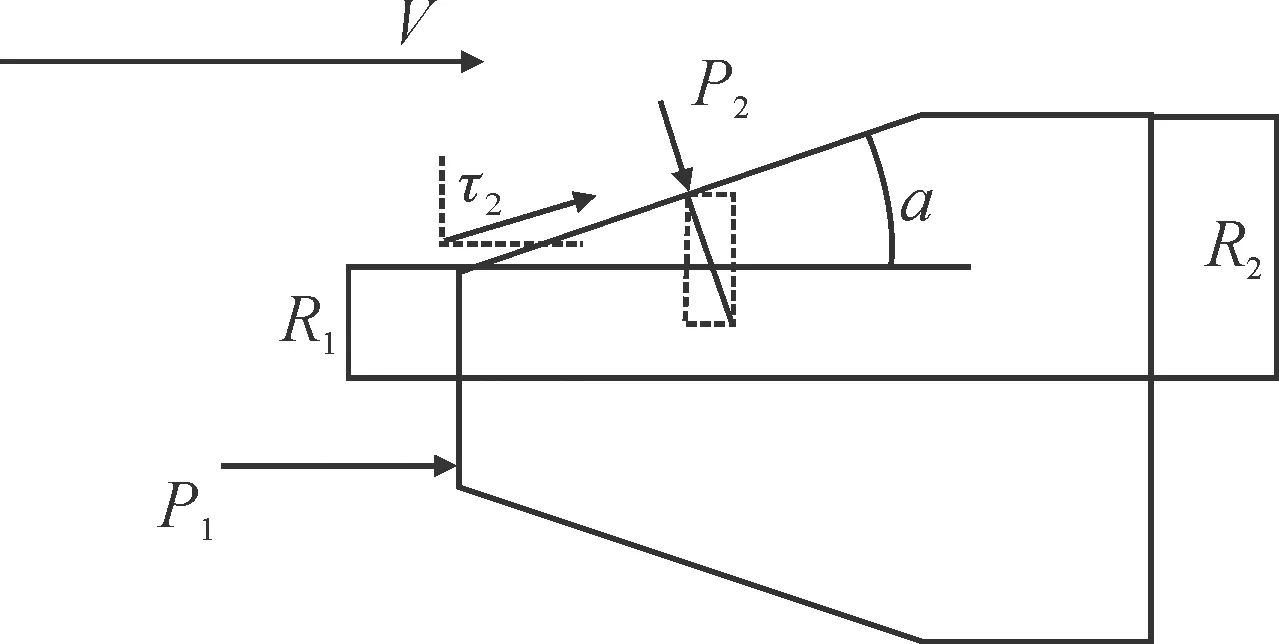
图1 平头弹头部形状示意图
根据压力的定义,有:
(1)
式中:P1为弹头前端面的压力,P2为弹头锥面处的压力,τ为弹丸的切向力,其方向与压力方向垂直。其中对上述力在轴向和垂直轴向的方向上进行分解,有:
P斜=P2sina+τ2cosa
(2)
由于斜面是曲面,构建曲面方程为:
(3)
则阻力为:
(4)
式中∑1为弹前端面面积。对式(4)进行求解可得:
(5)
从上述表达式可以看出,平头弹的阻力由两部分组成,一个是前端面的阻力,另一个是斜锥面上的阻力。
波阻的表达式为[3]:
(6)
式中:ρ∞为远场的流体密度;V∞为远场流速;SM为弹丸横截面积。所以,对于一定形状的平头弹丸只要知道压力P1、P2,切向力τ2,即可求出弹丸的头部阻力系数。
2 对波后压力的求解
上节已构建了任意形状的平头弹的阻力模型,并且将相关问题转化为求解压力P1、P2,切向力τ2。本节从空气动力学出发,构建求解平头弹的气动方程。
波阵面前后的气体状态如图2所示。从图2可以看出,对于平头弹,将会产生两个斜激波,激波1和激波2,由于文中讨论的是弹头的阻力情形,因此暂不讨论激波2的情况。为简化分析,假设:①波阵面前后的气体状态稳定,②流体为无粘性的。
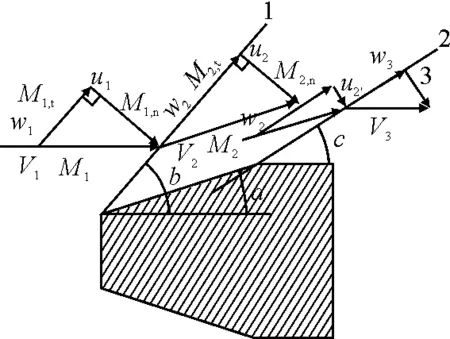
图2 波阵面前后气体状态示意图
利用已有结论[5],所需参量的求解如式(7)~式(10)所示。
(7)
(8)
(9)
(10)
式(10)表明,激波角只与来流马赫数和弹头形状有关,可以通过查表或数值计算的方法求解b的值。此外作用在弹头前端面的压力应该为动压与静压之和。值得注意的是,对于弹头阻力系数的压力,应取表压。
综合上式,平头弹的弹头阻力系数求解公式为:
(11)
式中:P为大气压力;P1为动压;b为激波角;γ为比热容比,取1.4。
从式(11)可以看出,平头弹的头部激波阻力与弹丸的平头半径,弹丸半径,半顶角以及速度大小有关。弹丸的速度越大,波阻越小;弹丸头部半顶角越小,波阻越小;弹丸平头半径越小,波阻越小。若取R1为0,则该模型即退化为锥形弹的波阻模型。
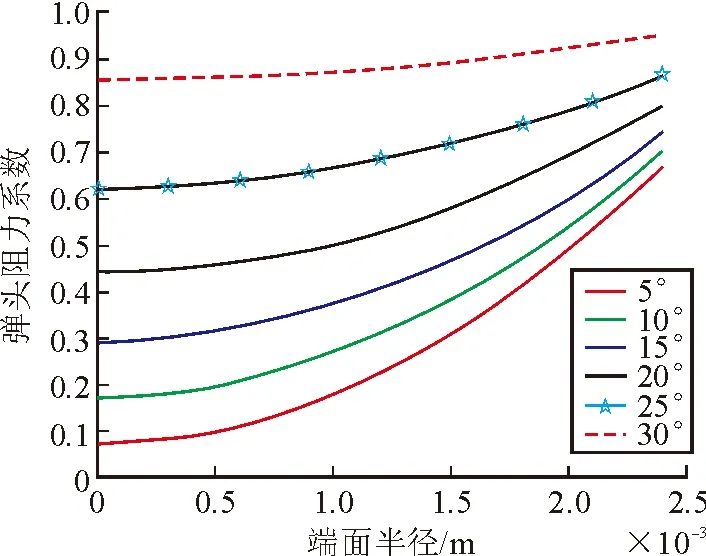
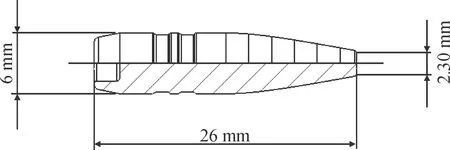
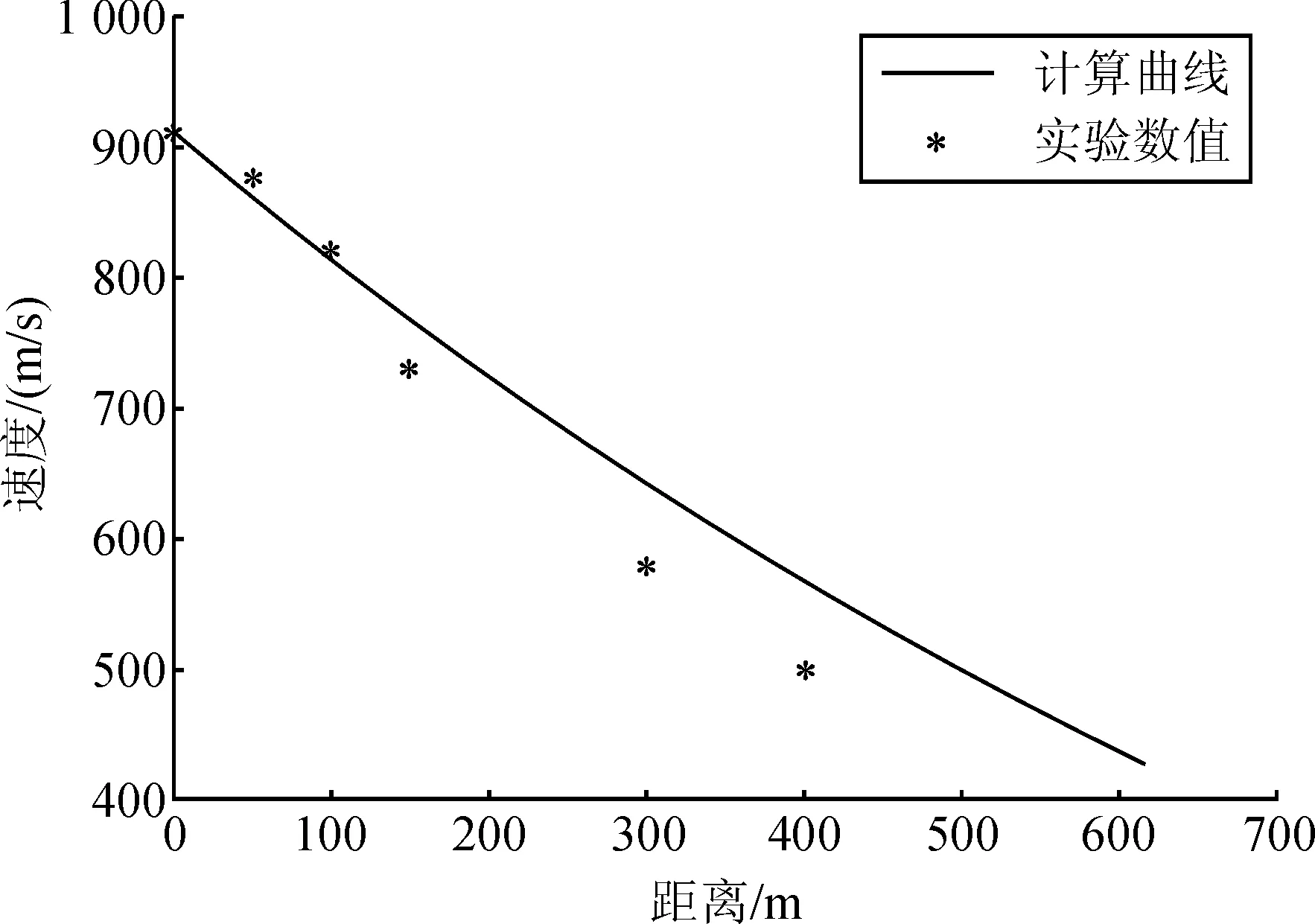
由于该模型是基于斜激波的理论建立,因此模型应用范围为1 应用Matlab软件,可以绘制阻力系数与弹头形状,速度的变化趋势图,能够更加直观地反映弹头阻力系数的影响因素。绘制曲线如图3、图4所示。 图3 不同端面半径和速度下弹头阻力系数(a=10°时) 图4 不同端面半径和半顶角下弹头阻力系数(Ma=2.8时) 平头弹的波阻系数表达式现已解出,结合现有的底阻和摩阻半经验公式,平头弹的阻力系数可以表示为: (12) (13) 将式(12)与质点外弹道方程式(13)联立,可以解得弹丸的外弹道运动轨迹。 为验证平头弹的阻力模型的正确性,对平头弹进行了外弹道试验,测量在各点处的速度降。平头弹实物图如下,其中弹丸的端面半径为1.15 mm,弹丸半径为3 mm,半顶角为10°。 图5 平头弹实物图 图6 平头弹尺寸图 对弹丸在各点处的速度记录如表1所示。 表1 弹丸各点处速度 联立式(12)、式(13)编制质点外弹道程序,弹道曲线如图7所示。 图7 外弹道计算曲线和实验拟合图 对外弹道实验所求数据与经过阻力模型计算曲线进行对比。可得该模型与实验结果趋势一致,且误差不大。因此,该模型可以较好地预测平头弹的外弹道特性。 文中根据空气动力学原理建立了平头弹阻力模型,利用该模型计算结果与外弹道实验所得数据吻合一致,证明了该平头弹阻力模型用于小口径平头弹外弹道计算时具有良好的准确性。本模型还涵盖了尖头卵形弹的弹道计算,可为小口径枪弹的设计提供参考。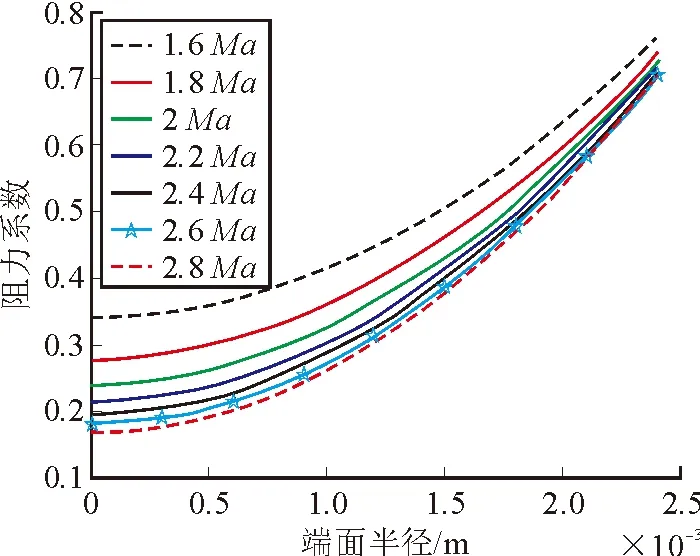
3 平头弹阻力系数表达式
4 试验验证


5 结论

