Age hardening process modeling and optimization of aluminum alloy A356/Cow horn particulate composite for brake drum application using RSM,ANN and simulated annealing

Chidozie Chukwuemeka Nwoi-Okoye,Basil Quent Ochieze

aFaculty of Engineering,Anambra State University(Chukwuemeka Odumegwu Ojukwu University),Uli,Nigeria

bDepartment of Mechanical Engineering,Chukwuemeka Odumegwu Ojukwu University,Nigeria

Keywords:Artificial neural network Response surface methodology Simulated annealing Age hardening Metal matrix composite

A B S T R A C T Most conventional ceramic based aluminum metal matrix composites(MMCs)are either heavy,costly or combination of both.In order to reduce cost and weight,while at the same time maintaining quality,cow horn particles(CHp)was used with aluminum alloy A356 to produce MMC for brake drum application and other engineering uses.The aim of this research is to model the age hardening process of the produced composite using response surface methodology(RSM)and artificial neural network(ANN),and to use the developed ANN as fitness function for a simulated annealing optimization algorithm(SA-NN system)for optimization of age hardening process parameters.The results show that ANN modeled the age hardening data excellently and better than RSM with a correlation coefficient of experimental response with ANN predictions being 0.9921 as against 0.9583 for the RSM.The SA-NN system optimized process parameters were in very close agreement with the experimental values with the maximum relative error of 1.2%,minimum of 0.35%and average of 0.71%.

1.Introduction

One of the principal requirements in automotive industry,which are the major driving forces for developing and implementing new materials,are fuel economy and emissions reduction.Heavier vehicles have greater inertia and greater rolling resistance and increased fuel consumption.Less weight means less power and fuel consumption.This also translates to less carbon dioxide emissions,which benefits the environment.

Aluminum and other light metals have lower density in comparison with the conventional materials used in the automotive industry(grey cast iron and steel).Their use helps to reduce vehicle mass,as well as increases efficiency;hence the basic requirements on fuel economy and vehicle emissions reduction are achieved.Despite this obvious advantage,their tribological properties are not wonderful which makes them not amenable for use in the production of tribomechanical vehicle parts.In order to solve this problem,the use of aluminum metal matrix composites(Al MMCs)is advocated[1].

Previous studies on brake drums,an important automotive component,showed that aluminum metal matrix composite(Al-MMC)automotive brake drums have high heat dissipation characteristics,better liner wear characteristics and less weight than similar size of cast iron brake drum[2].Also studies on the microstructure and mechanical properties of aluminum alloy A356 reinforced with silicon carbide and graphite particles reported significant improvement in hardness and tensile properties[3].Similarly,studies on the use of fly ash and red mud(an industrial waste)in reinforcement of aluminium/metal matrix composites yielded good results for wear resistant applications and improved engineering properties [4,5].Unfortunately,all these reinforcements reported in earlier researches were either heavy,costly or a combination of both,hence the use of aluminum alloy A356/cow horn particulate(A356/CHp)composites was proposed as an alternative because of its cheapness,lightness and good mechanical properties(hardness and wear resistance).As stated above,hardness is an important mechanical property of brake drums and numerous engineering components and materials.

Modeling and prediction of the mechanical properties of engineering materials is an extremely important component of engineering analysis.The use of mathematical models,often based on regression analysis,have been the earliest tool available to the engineer for modeling the properties of engineering materials[6,7].However,in recent times,due to great advances in information and computer technology,artificial intelligence and soft computing techniques are increasingly replacing mathematical models in modeling properties of engineering materials[8,9].Computational models are often favoured over mathematical models because they are easier to develop and are often more accurate than mathematical models[6,9-11].

Artificial neural networks(ANNs)have been a dominant computational method of modeling the properties of engineering materials.Several researchers have successfully applied ANN to model properties of engineering materials.Such researchers include:Atuanya et al.[10]who used ANN to model the mechanical properties of date palm fibre-polyethylene composite,Nwobi-Okoye and Umeonyiagu who carried out extensive research on the use of ANN for prediction of the strength of concrete made with concrete making material sourced from the east of Nigeria[6-9,12]and several other researchers.Of numerous mathematical models used in modeling engineering materials,response surface method is a very popular method used extensively.Suresh et al.[13]used response surface methodology to predict the Mechanical properties of stir cast Al-TiB2 composites.Similarly,Rostamiyan et al.[14],modeled the effect of weight percentage of nano silica,nano clay and fiber orientation on tensile and izod impact strength of epoxy/glass fiber/SiO2/clay hybrid laminate composite.These two works typifies the numerous applications of RSM in modeling material properties.

Quite often it is necessary to optimize process parameters during the development of materials used for engineering applications.Several optimizations techniques such as genetic algorithm,particle swarm optimization,simulated annealing etc have been used in this regard[15,16].Sometimes because of the accuracy of ANN in modeling processes,they are sometimes used as fitness functions to the optimization algorithms[15,16].

The aim of this work was to model the hardness of metal matrix composite(MMC)produced from cow horn(CHp)and aluminum alloy(A356)metal.The hardness was modeled using response surface methodology(RSM)and artificial neural network(ANN)and a performance comparison made between the two models.Subsequently the hardness values were optimized using simulated annealing optimization algorithm with the ANN as the fitness function.

2.Experimental procedure and composite production method

2.1.Production of composite samples

2.1.1.Mixing process

The mixing of A356 powder and CHp reinforcement particles was done using a 3D inversion mixer.The materials were put in a tungsten mixing jar which contains 50 tungsten milling balls that are 10 mm diameter(the ball to powder weight ratio was 5:2).The mixing was done at room temperature for a time duration of 8 h.This was done to obtain good dispersion/distribution of reinforcements in the aluminum matrix.For more details of the mixing process see Ochieze[20],Ochieze et al.[21]and Basil et al.[22].

2.1.2.Spark plasma sintering(SPS)

The aluminum matrix composites samples was processed using a spark plasma sintering machine(model SPS 10-3),manufactured by Thermal Technologies LLC.The SPS equipment is provided with a hydraulic pump which can generate a force of up to 100 kN.Graphite dies and punches were used to fabricate samples at low pressures(≤100MPa).Thermocouples,K type and C type were used to measure the die temperatures during the experiments.

Compaction of materials using spark plasma sintering machine is mainly achieved by placing materials in-between dies and punches at a required temperature and pressure.The desired temperature and pressure determines the choice and design of dies,punches,and spacers.Aluminum matrix composites sintering is considered a low temperature and low pressure sintering process because the melting point of aluminum is ～660°C.Based on the wide availability,ease of machining and high thermal and electrical conductivities at elevated temperatures of graphite,it is the most widely used material for making dies and punches for spark plasma sintering.Generally,graphite dies and punches are used to sinter aluminum matrix composites below 30 MPa.In this work,the sintering was performed at a temperature of 550°C and pressure of 30 MPa.For more details of this process see Ochieze[20],Ochieze et al.[21]and Basil et al.[22].

2.1.3.Production of bulk samples of A356/CHp composite

The A356 alloy of composition shown in Table 1 was used for the research.

The A356 matrix/xCHp(x=0,5,10,15,20)composite samples were produced using spark plasma sintering.Samples of dimensions,diameter 100×5 mm,weighing about 103 g were produced using graphite dies and punches.The composites were produced at 550°C and 30 MPa with heating and cooling rate of 100°C/min.The thermocouple was inserted into the bottom punch to measure the temperatures of the process.All the samples were produced in a closed furnace where 2-10 torr vacuum was maintained throughout the experiment.For more details of this process see Ochieze[20],Ochieze et al.[21]and Basil et al.[22].

2.1.4.Cutting of the samples

Circular,rectangular and square shaped specimens for analytical tests and heat treatment were cut out from the produced sinters as shown in Plate1.The cutting was done using Robofill 240 automatic cutting machine.

2.2.Thermal treatment of the samples

The test samples were solution heat-treated at temperature of 520°C in an electrically heated furnace,soaked for 3h at this temperature and then rapidly quenched in warm water at 65°C.Thereafter,the samples were thermally aged at temperatures of 150°C and 350°C,for various ageing times until the peak ageing was exceeded.The ageing characteristics were evaluated using hardness values obtained from the solution heat-treated and thermally aged samples.For more details see Ochieze[20],Ochieze et al.[21]and Basil et al.[22].

2.3.Determination of hardness values

The hardness values of both as-sintered and thermally agehardened samples were determined according to the provisions of American society for testing and materials(ASTM E18-79).Rockwell hardness tester on scale “B”(Frank Welltest Rockwell Hardness Tester,model 38506),with 1.56 mm steel ball indenter,major load of 100 kg,minor load of 10kg and 101.2HRB standard block,was utilized for the research.Prior to running the test on the specimens and calibration of the testing machine using the standard block,the mating surface of the indenter,plunger rod and test samples were thoroughly cleaned of dirt,scratches and oil.Thereafter,the samples were put on the anvil which supported the test samples.Initially a minor load of 10 kg was applied to the sample in a controlled manner without inducing impact or vibration and when a zero-datum position was established,the major load of 100kg was then applied.Experimental readings were taken from the hardness tester when the large pointer came to rest or when it had slowed very well and stayed steady for up to 2 s.Thereafter,the load was taken out by returning the crank handle to the latched position,and the hardness value was subsequently read off directly from the digital scale.For more details of see Ochieze[20],Ochieze et al.[21]and Basil et al.[22].

Table 1 Composition of the A356 alloy.

2.4.Statistical design analysis and development of mathematical model for the thermal ageing process

The statistical experimental design was based on two levels and three factors for each level.The levels for the three factors are as shown in Table 2 and Fig.1 and the treatment combinations for the two levels and these three factors were tabulated in Table 3.

Although CHp particle size affects the mechanical properties,a CHp particle size of 150μm was used in the production of the composite based on the recommendations from literature for optimum mechanical properties.Hence,the particle size was not varied nor used as a variable in the age hardening process.

Representing the hardness value byH,the responsefunction can be expressed in the form stated in Equation(1):

WhereAT=Ageing temperature.

The model selection was based on the effects of main variables as well as the first-order and second-order interactions of all variables.Consequently,the general model is written as stated in Equation(2):

Table 2 Statistical experimental design of the thermal ageing process.

Where βois average response ofWand β1,β2,β3,β4,β5,β6,β7are coefficients associated with each variableAT,CP,Atand interaction.

3.Artificial neural networks(ANNs)

Artificial neural networks(ANN)are computational modeling tools often employed in modeling input output relationships of systems or processes where it is difficult or impossible to find mathematical models for defining such systems.ANN was inspired by the network of neurons in the brains of living organisms which enable them to act intelligently.Artificial neural networks use of artificial neurons as computational tools.Artificial neural networks(ANNs)mimic the manner of operation of natural neurons in living things.Most ANN's are feed forward multilayer perceptron networks.Feed forward networks use backward propagation algorithms for learning.Some learning algorithms include but not limited to gradient descent algorithm,Levenberg-Marquardt algorithm,genetic algorithm etc[6,17,18].ANN consists of several nodes which represents the neurons.The input nodes represent the independent variables while the output nodes represent the dependent variables.

This study used ANN to accurately model the age hardening process of aluminum alloy A356/CHp particulate composite.Accurate prediction of the parameters of any process is critical to the quality,economics and optima performance of the process.Once a satisfactory ANN model is developed,the model is integrated into an optimization procedure known as simulated annealing,as its fitness function,to optimize the age hardening process parameters.The ANN inputs consisted of temperature,percentage composition of cow horn particles and time,while the output consisted of the hardness values.

4.Simulated annealing

According to Piuleac et al.[11],conventional optimization methods consist of two methods:direct search methods and gradient methods.Direct search methods,such as simplex algorithm,use the objective function and constraints to search for the optimum.Gradient methods use calculus(differentiation)to obtain optimum values.Direct search methods which are considered to use brute force are slow and the gradient methods fails if the function is discontinuous or non differentiable.These deficiencies gave rise to the invention of metaheuristics which includes natural optimization algorithms.Simulated annealing(SA)is a metaheuristics method that belongs to natural optimization algorithm.

Simulated annealing(SA)is an optimization method that mimics the process of annealing used in metallurgy to harden materials by raising their temperature and gradually lowering it to ambient temperature.Simulated annealing is a variant of metropolis algorithm,a process for simulating the evolution to the thermal equilibrium of a solid at a given temperature.SA differs from metropolis algorithm in the fact that in SA the temperature moves from high to low.SA is a gradual descent algorithm moderated by random ascents aimed at escaping local minima which are not global minima.SA comprises of two stochastic processes.One of the processes is responsible for the generation of solutions and the other for the acceptance of generated solutions.It is been proved that given sufficiently large number of iterations at each temperature,SA will almost surely converge to the global optimum[19].

Table 3 Factorial design of the ageing process showing treatment combination.

5.Results and discussion

5.1.Experimental results

5.1.1.Hardness values

Figs.2-3 show the hardness values(HV)as a function of aging time at 150 and 350°C for the alloy and composites.A reduced hardness of the matrix was observed as compared with reinforced alloy.The times required to attain the peak hardness for samples artificially aged between 150°C and 350°C are summarized in Tables 4 and 5.The presence of CHp in the matrix decreased the time needed to achieve the peak hardness.This suggests that the addition of CHp to the matrix causes considerable acceleration in the aging kinetics of the composite.Increase in the aging temperature from 150°C to 350°C leads to a decrease in the time to obtained peak hardness of the samples(see Figs.3-4).

The included CHp particles in all experiments were generally high so that their effect on hardness improvement would gradually increase as the proportion increases.But the limit of the CHp content was 20 wt%CHp as shown in Figs.2 and 3.At 25wt%CHp,there was over shooting of temperature to 650°C and melting of the aluminium alloy was observed(an undesirable effect).Also,effect such as melting out the matrix from the mould was observed with 25wt%CHp sample,for these reasons the 25 wt%CHp was not considered in the research.See Ochieze[20]for details.

Strength increasing mechanisms involve the increase in hardness due to grain refinement(Hall-Petch relationship),the hindering effect of the particles on dislocation motion as well as the accumulation of dislocations due to the different thermal expansion of the ceramic particles and the matrix material(see Fig.4).

There exists a significant coefficient of thermal expansion mismatch between the matrix and the CHp,which would result in the prismatic punching of dislocations at the interface leading to work hardening of the matrix.The dislocation density generation is likely to be higher,which in turn would result in increasedstrengthening.Incremental strength, Δσ=αμρ(1/2)bwhere α=constant=1.25,μis the modulus of rigidity of the matrix(Al),bis Burger's vector.Dislocation density(ρ)is given by ρ=10Aε/(bt(1-A)),whereAis the reinforcement(CHp)wt%,ε is thermal strain,bis Burger's vector,andtis the dimensions of the reinforcement.

Table 4 Results of age-hardening of the composites.

Table 5 Hardness values of A356 alloy/CHp composites.

The decreased in the hardness values after the optimum point has been reached can be attributed to the over-ageing of the composites.Also,the decrease in hardness values of the unhardened samples can be explained by the contribution of inter-atomic spacing due to strain hardening which arises from the fact that the inter-atomic spacing permitted a dislocation to maneuver round obstacles.The hardness values are given by the formula:

τ=τ=hardness values,λ=Inter-particle spacing,G=Shear energy of dislocation andb=Burger vector.

The smaller the values ofλ,the greater the hardness values due to strain hardening.A testament to the fact that the microstructures displaced above with smallerλhave greater hardness values than those with largerλ(coarse structures).This shows that dislocations cause the hardness increase in alloy and also residual stress increase due to the fact that it acts as non-uniform nucleation sites in the interface due to the heat treatment.The scientific explanation for this is that as the quantity of fine grain sizes in the composite increases,the density of dislocations equally increases resulting to increase in hardness of the composite material.

The fine-grained structure and the dispersed nature of the precipitates contained in the fine grained structure of the matrix restricts the smooth movement of dislocations resulting to the high hardness of the peak ageing.The samples became finer grained due to the fact that the precipitates interfere with the nucleation growth process.Thus,the precipitates enhanced nucleation by creating disorder in the incorporation of atoms into the lattice or inhibition of the surface diffusion of atoms towards growing centres and exert a detrimental effect on the crystal growth.This effect of grain refining is beneficial for the hardness values of the samples.From Fig.4,the hardness values of as-produced and age-hardened composite samples increased as the percentage of CHp addition increases in the composite.This is due to increase in the percentage of the hard and brittle phase of the ceramics body in the composite.The improvement obtained in hardness values of the composites which ranges from 70 to 80 HRB is within the limit for brake rotors produced with aluminum composites[23].

5.2.Response surface modeling results of A356/CHp

5.2.1.Model for prediction of thermal ageing behaviour

The test results were recorded against the standard order of sequence as shown in Table 6.The sum of squares for main and interaction effects was calculated using Yates algorithm.The significant factors(main and interaction)were identified by analysis of variance technique using design expert software.

The developed model equation for the hardness values of the composites can be expressed as:

From the model equation,it was observed that the coefficient ofA(temperatures)is positive,that ofB(wt%CHAp)is positive,that ofC(time)is positive and the interaction betweenABis positive andBCis negative.This means that by increasing the ageing temperature from 150 to 350°C increased the hardness values by 1.51,by increasing the ageing time from 1 to 15 h increased the hardness values by 0.73,while by increasing the reinforcement from 0 to 20 wt%also increased the hardness values by9.32 and by increasing the temperature and reinforcement at the same time increased the hardness values by 1.19,but by increasing the ageing time and reinforcement at the same time decreased the hardness values by 4.54.

These explanations can be clearly seen from Figs.5-8.From Figs.6-8,it can be seen that the hardness values of the composites are highly influenced by the reinforcer(wt%CHp).For example,as reinforcer increased from 0 to 20 wt%,the hardness values also increased(see Figs.5-8).

Substituting the coded values of the experimental variables in the response surface model of Equation(1),the hardness values for the composites for any parameter combination can be determined.Fig.9 shows the predicted hardness values and the actual experimental values in varying experimental conditions.

As shown in Fig.9,the actual experimental values are in close agreement with the predicted values.A prediction error of less than 1.5%shows that the model equation is a very reliable tool for predicting the hardness values with a reasonably high degree of accuracy.

ANOVA was used to determine the design parameters which have significant effects on the hardness values.The values ofFcalculated(F=Fishers distribution)were compared withFcritical.Fdistribution critical values for degrees of freedom(1,7)at 95%confidence level(see Table 7).The Model F-value implies the model is significant.There is only a 0.65%chance that a “ModelF-Value”this large could occur due to noise.

Values of“Prob ＞F′′less than 0.0500 indicate model terms are significant.

In this caseB(wt%CHp),BC(interaction between wt%CHp and ageing time)are significant model terms.

The“Pred R-Squared”of 0.9583 is in reasonable agreement with the “Adj R-Squared”of 0.9909.

Correlation coefficientRwas used to determine the adequacy of the developed model as shown in Table 7.The calculated value ofRobtained in this study is 0.9583,which shows that the hardness values obtained from the developed response surface model has high correlation with the experimentally determined values.

5.3.The network architecture and characteristics

The feed forward backward propagation neural network was used because the application was for prediction.The optimum network performance was reached at an epoch of 18.The epoch was set at 1000 to ensure that the network was well trained beforetesting and validation.The number of hidden layers which gave optimum performance was10.The training algorithm was levenberg-marquardt which performed better than others.One hundred and fifty(150)experimental inputs and responses were used for ANN training,testing and validation.Seventy percent(70%)of the data(104)were used for training,while fifteen percent(15%)each(23)were used for testing and validation respectively.

Table 6 Standard order of test sequence and result.

The network architecture consists of three input units,ten(10)hidden layers and one output unit as shown in Fig.10.This structure performed better than other configurations that we tested.The inputs consist of temperature,percentage composition of cow horn particles and time,while the output consists of the hardness values.

The mean squared error(MSE)of the trained network at the point of minimum validation error was 0.75,theMSEof the validated network was 1.2272,while theMSEof the tested network was 1.8.TheMSEare as shown in Fig.11.The best validation performance occurred at the epoch of 12 as shown in Fig.11.The regression coefficientRof the trained network was 0.99452 as shown in Fig.12 while the overall regression coefficient(training,testing and validation)was 0.99214 as shown in Fig.13.

Table 8 shows some ANN predictions of the experimental responses.Table 8 was used to plot Fig.13.As shown in Fig.13 and stated earlier,the overall regression coefficient for the network was 0.99214.The regression coefficient of the RSM model was 0.9583 as earlier stated.

5.4.Optimization procedure

A MATLAB function which is a well trained ANN as previously described was used as the fitness function for a simulated annealing algorithm used to carry out the optimization of the coagulation process.The upper and lower limits of the experimental variables were used as the upper and lower bounds of the optimization algorithm.The starting point of the optimization was the values of the experimental variables that gave the highest efficiency.The negative values of the hardness were used because the objective of the simulated annealing algorithm is to minimize the objective function.

The simulated annealing algorithm used has the following settings.

Initial temperature(IT):100.

Temperature function:IT*0.95kwherekis the annealing parameter.

Annealing function:@annealfast.

Re-anneal interval:100.

Acceptance function:

Stopping criteria:TolFun(1.0000e-06).

Table 9 shows the optimum process parameters for some percentage compositions of cow horn particles in the composite.The simulated values obtained from the simulated annealing algorithm are in very close agreement with the experimental values.

As shown in Table 9,assuming the percentage composition of cow horn particles wanted in the composite is 8%,what temperature and treatment time will give the optimum hardness?The optimization result shown in Table 9 answers the question by recommending ageing temperature of 350 and ageing time of 7.3 with simulated hardness value of 71 very close to experimental value of 71.87 with a relative error of 1.21%.The simulated optimum hardness values shown in Table 9 are very close to the experimentalresult with maximum relative error of 1.2%,minimum of 0.35%and average of 0.71%.

Table 7 Analysis of variance table to identify significant factors influencing hardness.

6.Conclusions

The following conclusions could be drawn from this study:

(i.)Response surface methodology could be used to model the agehardening process of A356 alloy/CHp particulate composite.

(ii.)ANN is an excellent tool for modeling the age hardening process of A356 alloy/CHp particulate composite.

(iii.)ANN is a much better tool than RSM in the prediction of hardness values obtained from age hardening of A356 alloy/CHp particulate composite.

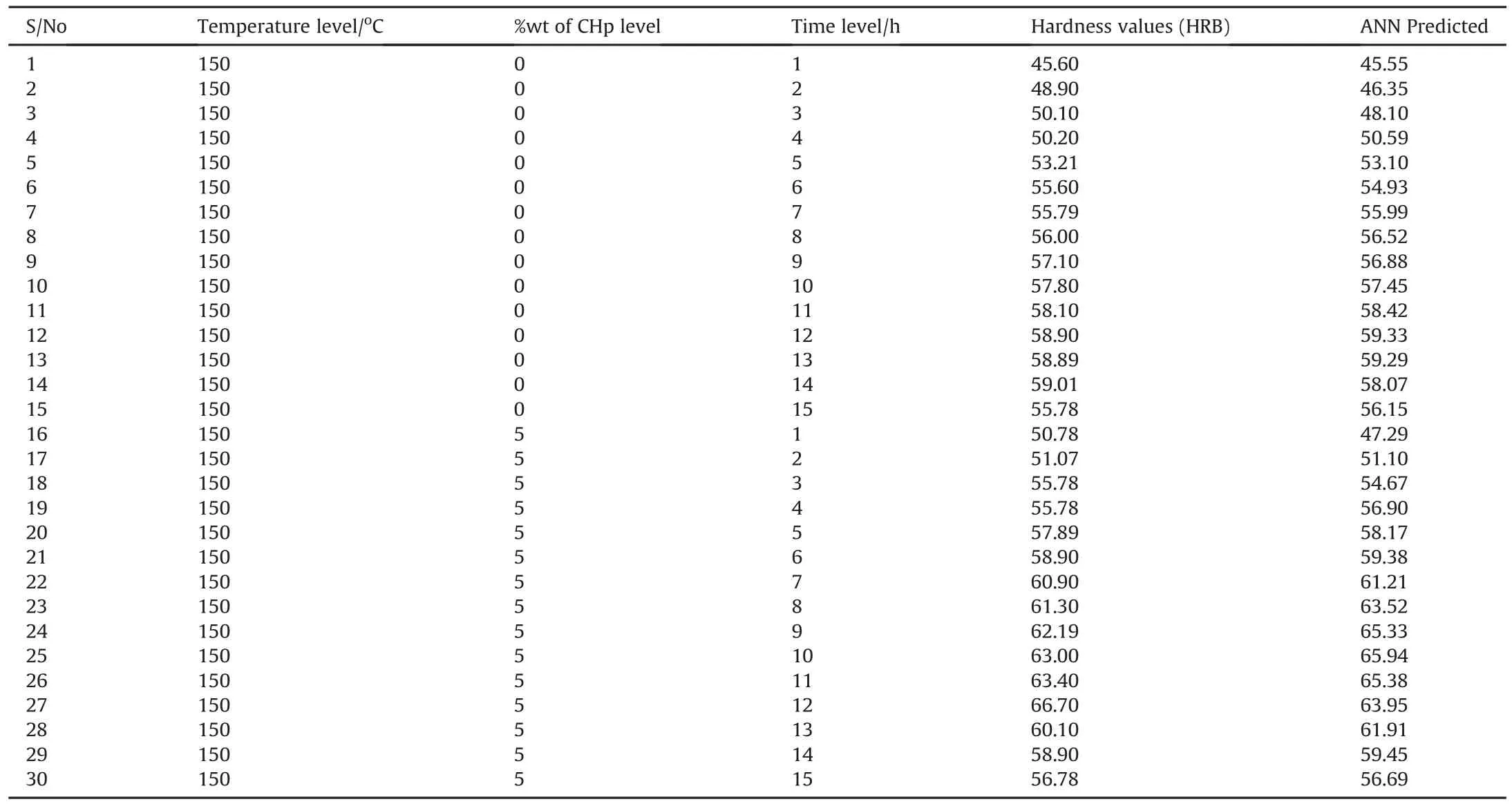
Table 8 Some experimental responses and predicted responses.

Table 9 The process parameters that gave the optimum efficiency.

(iv.)Simulated annealing with ANN as fitness function(SA-NN system)is an excellent tool for optimization of process parameters in age hardening process of A356 alloy/CHp particulate composite.

(v.)The developed models have a general character and could be applied to any age hardening process.