水下机器人惯性导航系统

李秦牧，朱大奇，邓志刚

（上海海事大学信息工程学院，上海 201306）

0 引言

海洋面积十分广阔，占据着整个地球十分之七的面积。广袤的海洋蕴藏的种种未知刺激着人们无尽的求知欲望，人类逐渐认识到对于海洋资源的开发与利用的重要性。水下机器人因为其能有效的帮助人类完成水下持续探索，深海工作等水下工作优势，成为人类科学研究的重点。为了应付水下的复杂环境，路径导航成为关键。本次以“海鲨”ROV水下机器人为模型作为仿真对象，选用捷联惯导系统完成水下运动的路径导航，通过仿真以验证算法的可行性，同时确保3分钟航行的绝对误差在2.5米以内。

1 惯导的基本介绍

惯性导航是当代技术科学中的一门新兴的研究领域，将惯性导航技术运用到水下机器人中可以满足现代化水下搜索工作。

导航就是指运动目标从起点出发，沿着事先规划的航线在沿着规定轨迹到达目的地。自古以来，人们学会利用自然环境进行导航，例如天上星宿中的北极星来确认方向。随着时代的前进，现代科学的飞速发展，导航逐渐发展成为一门具体研究导航理论方法与导航技术器件的学科[1]。

而在所有的导航体系中，惯性导航系统是唯一在真正意义上能够实现自主导航的系统，惯性导航系统能够根据运载体测试得到的加速度、角速度、航向角、横向角等信息，仅仅依靠运载体自身实现自主导航的任务。

惯性导航的基本原理是在牛顿经典力学的基础上，依靠挂载在运载体上的惯性元件测量得出加速度、角速度、航向角等信息，通过数学运算解析的方式，计算得出运载体的位置定位信息。虽然惯性导航的理论基础较为简单，但是在实际应用中就会面临诸多困难，例如高精度的惯性器械元件，高计算速度的计算机，可靠高效的惯导系统。随着科学技术的进步，这些问题才逐渐解决，惯性导航系统才出现实际运用的可能性[2]。

惯性导航系统可以分为两类，一类称为平台惯性导航系统，而另一类称为捷联惯性导航系统。在平台式惯性导航系统中，将陀螺仪和加速度计等惯性元件安置在一个物理平台上，利用陀螺仪和加速度计等惯性元件，模拟得到一个导航坐标系，为加速度计提供一个标准的坐标模板，也保持了三轴加速度计始终沿着既定方向进行测量，同时也使惯性测量元件和运载体的相对运动保持稳定。

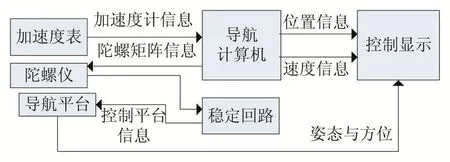
图1 平台式惯性导航系统原理

但是平台式惯导需要高精度的相对水平平台，这种水平平台不仅占地面积较大，而且受到工艺的复杂性和精密度制约，所以成本十分昂贵。限于外界条件的限制，平台式惯导的实际应用受到很大的制约。

而捷联惯系导航系统不在需要实体平台，将陀螺仪和加速度计这类惯性元件直接安置于运载载体，惯性元件的检测轴安装在与载体坐标系的三轴相平行的三个方向上。在运载体的实际航行过程中，惯性元件测量得到运载体相对于惯性坐标系的角速度，再通过矩阵变换，得出载体坐标系至导航坐标系的坐标变换矩阵，即姿态矩阵。然后再运用姿态阵将加速度计测得的加速度信息进行矩阵运算，并融合进入导航坐标系中进行导航计算，也就是说姿态矩阵代替了实体平台，充当着“数学平台”的作用，得到的载体姿态与速度为[3]：

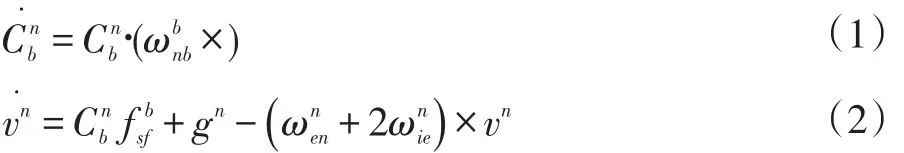
通过上面两个公式就可以求得数学平台的姿态矩阵已经比力变换参考，以代替平台式惯导中模拟的地面水平面以及加速度计直接读出的三轴导航方向的加速度值。

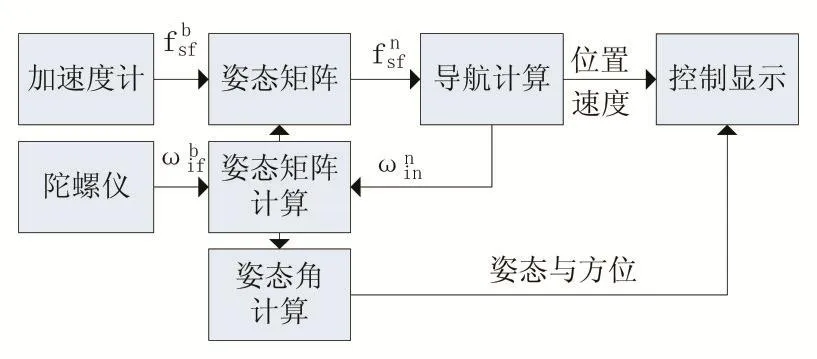
图2 捷联惯性导航系统原理

考虑到平台惯导在实际应用受到的条件约束，捷联惯导的优势可以总结为4条：

（1）节约了绝对水平的惯导平台，大小、面积、重量以及成本大大降低；

（2）捷联惯导的惯性元件可以直接的读出运载体的加速度、角速度信息，这些都是进行姿态变换的计算必要信息；

（3）大大提高系统的性能以及可靠性；

（4）捷联式惯导系统的初始对准快捷方便。

因此结合以上优点，“海鲨”ROV水下机器人选用捷联惯导作为本次实验的导航系统。

2 捷联惯导的数学算法

水下机器人的导航在地球上进行的，定位和定向都是相对于地球球面而言的。经度、纬度和高度是导航的重要计量参数，重力加速度是导航的基本自然参考量。为实现水下机器人捷联惯导系统，一方面需要完成坐标系之间的转换，实现姿态转换，另一方面需要设计得到捷联惯导算法[4]。

2.1 坐标轴的定义以及变换

（1）坐标系定义

①载体坐标系b系：用oxbybzb表示，o点位于船体的重心，xb轴沿着船体横轴向右，yb沿着船体纵轴向前，zb沿着船体竖轴向上。载体坐标系和矫正坐标系的方位关系可以用姿态矩阵或者姿态角、方位角来表示。

②矫正坐标系t系：用oxtytzt表示，陀螺仪和加速度计的3轴应该与船体的3轴对齐，但实际情况中总有不对准角的存在，对导航的精度有着不良的影响，为了提高精度需要校准精度角。o点位于船体的重心，xt轴沿着校准后船体横轴向右，yt沿着校准后船体纵轴向前，zt沿着船体立轴向上。矫正坐标系和导航坐标系的方向关系可以用姿态矩阵护着姿态角、方位角来表示。

③导航坐标系n系：用oxnynzn表示，它是导航系统在求解导航参数时所采用的参考坐标轴。o点位于船体的重心，xn轴指向东（E），yn轴指向北（N），zn轴指向天顶（U），即俗称为东-北-天（E-N-U）坐标系。

（2）坐标系之间的变换关系

①载体坐标系和校正坐标系之间的关系

惯性传感器（陀螺仪与加速度计）的安装偏差角主要包括位置的错位和未校准角。与飞机不同，ROV在行进过程中没有高速的角运动，正因为如此，位置的错位是可以忽略的，只需要考虑未校准角[5]。

因为IMU被安装于船体的质心，校正坐标系t的原点与载体坐标系b的原点重合。在船体运动过程中偏差角也就是图所示的Δx,Δy,Δz。

所以从t到b的变换矩阵为公式（3）：

其中Δx，Δy，Δz为偏差角，所以数值较小，因此上式可以简化为：

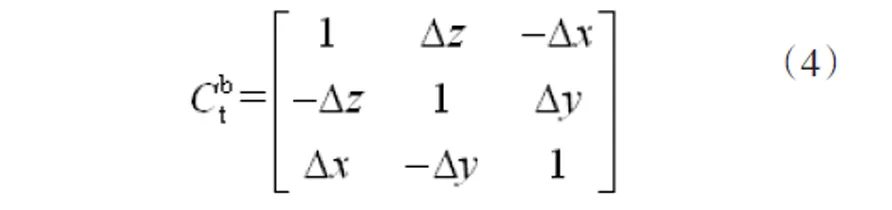
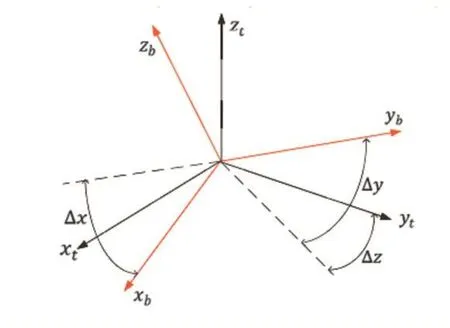
图3 安装偏差角

Δx，Δy，Δz是在校正坐标系t中测量的，所以从载体坐标系b到校正坐标系t的矩阵变换为，也就是：

（2）载体坐标系到导航坐标系之间的变换关系

俯仰角（pitch）：可以用θ表示，载体坐标系x轴与水平面的夹角。当x轴的正半轴位于过坐标轴原点的水平面之上时，俯仰角为正，否则为负，也是说俯仰角是围绕x轴旋转的。

横向角（roll）：可以用γ表示，载体坐标系zb轴与通过载体xb轴的铅垂面的夹角，载体向右滚为正，反之为负。也就是说横向角是围绕z轴旋转的。

航向角（yaw）：可以用ψ表示，载体坐标系xb轴在水平面上投影与地面坐标系xg轴（在水平面上，指向目标为正）之间的夹角，由xg轴逆时针转置载体xb的投影线时航向角为正，即载体右航向为正，反之为负。也就是说航向角是围绕y轴旋转的。

导航坐标系oxnynzn绕zn轴负向转角ψ得ox'y'z'，ox'y'z'绕 x'轴转角 θ得 oxnynzn，oxnynzn再绕 yn轴转角γ则得到矫正坐标系oxtytzt（旋转顺序不能改变），因此矫正坐标系与导航坐标系之间的关系用方向余弦阵可以表示为公式（6）。

所以，如公式（7）。

仅考虑航向角转动的情况下可以得到：

假设：

其中：

所以由姿态矩阵提取姿态角如下：

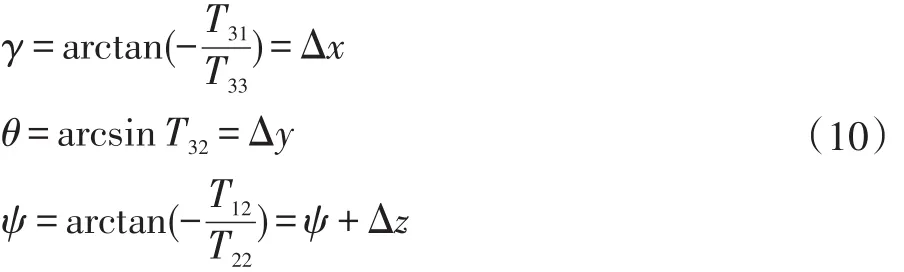
2.2 接连惯导数字迭代算法

（1）姿态更新算法

选用的是东-北-天（E-N-U）坐标系作为接连惯导系统的导航参考坐标系，则姿态微分方程为：

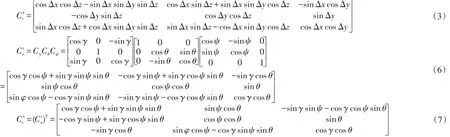
式中，角标括号中的m表示tm时刻。因为i系是一个绝对惯性参考系，所以它与时间无关，而n系和b系相对于i系是动坐标，均与时间有关，需要标注时间[6]。

其中Arot为陀螺仪得到的角速度，为：

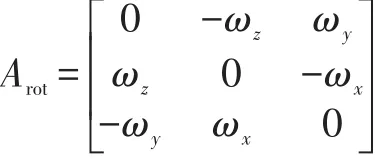
上式即为接连惯导递推姿态更新算法。

（2）速度更新算法

对上式在[tm-1,tm]时间段内两边做积分可得：

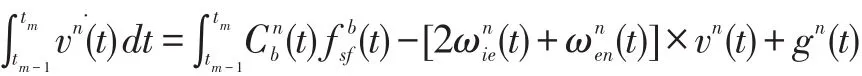
展开可得：

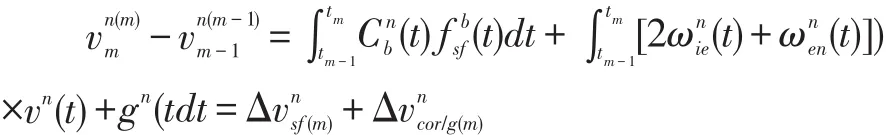
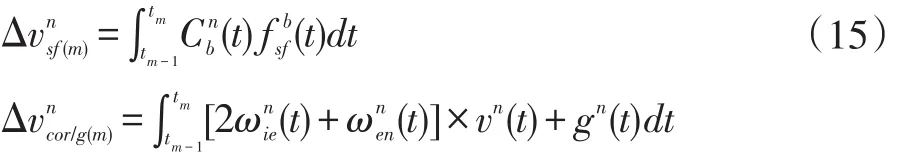
所以将上式可以改写为：

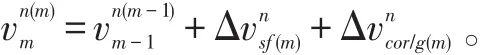
因为ROV在水下航行时，短时间[tm,tm-1]内引起的导航坐标系旋转和重力矢量变化都十分小，因此一般认为的被积函数可以忽略不计。所以只需要考虑[tm,tm-1]时间段内比力速度增加量。

（3）置更新算法

捷联惯导系统位置微分方程为：

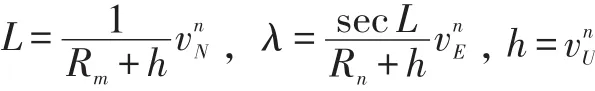
将经度、纬度、高度改写为矩阵形式可以得到：p=Mpvvn。

其中记：

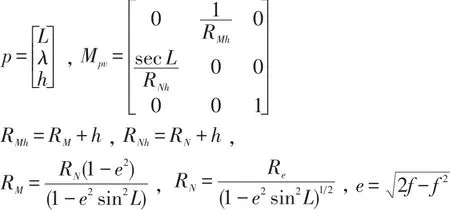
对上式在[ ]tm-1,tm时间段内两边做积分离散化可得：

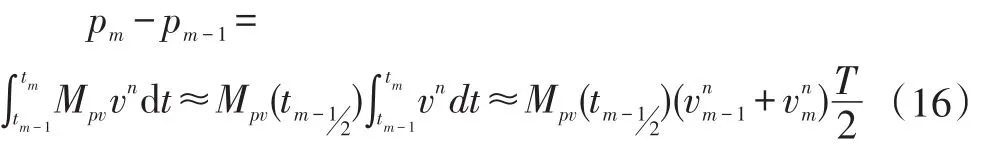
移项后就可以得到位置更新算法：

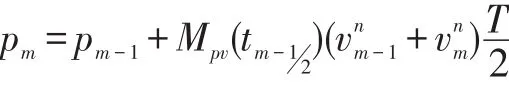
3 仿真与测量结果

进一步简化可以得到：

前一节已经给出基于水下机器ROV的捷联惯导算法，这里对于所提出的算法进行仿真分析，验证算法的有效性，并且与实际GPS路径进行比较，验证算法的精度。仿真结果主要分为两部分：捷联惯导位置推算路径仿真与推算路径与实际GPS轨迹的比较。同时需要满足航行3分钟位置绝对偏差控制在3.5米以内。

捷联惯导位置推算路径仿真，设计出水下机器人ROV导航系统框图如图4所示。

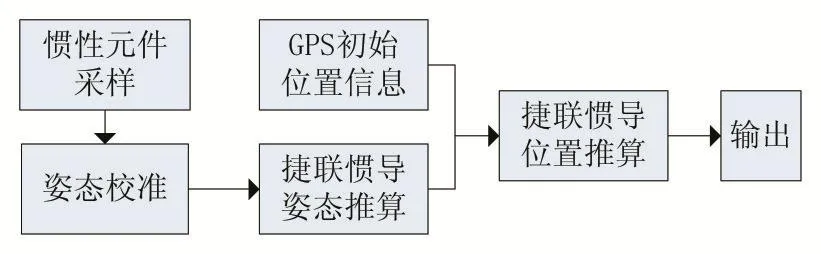
图4 导航系统框图

首先惯性元件陀螺仪和加速度计采样到各时刻运载体的角速度和加速度，从而可以得出姿态矩阵，再通过姿态校准将安装偏差角的误差消除，然后经过捷联惯导算法推算出下一时刻的姿态，再结合GPS读出的初始航向角，推算出导航的位置，继而实现惯性导航。

根据惯性元件采集到的数据，进过捷联惯导系统推算后得到的仿真导航路径如图5所示。

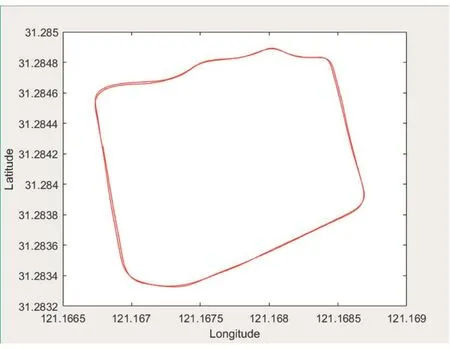
图5 捷联惯导推算路径

图中，x轴为经度，y轴为维度，蓝色实线即为捷联惯导推算得到的路径。为了直观的检验捷联惯导算法的准确性，将推算路径与GPS得到的实际轨迹进行比较，如图6所示。

图中，红色实线为捷联惯导推算轨迹，蓝色实线为GPS实际轨迹。可以看出捷联惯导推算得到的路径与GPS实际轨迹能够保持较高的重合度，并未出现重大误差的情况。而绝对误差如图7所示。

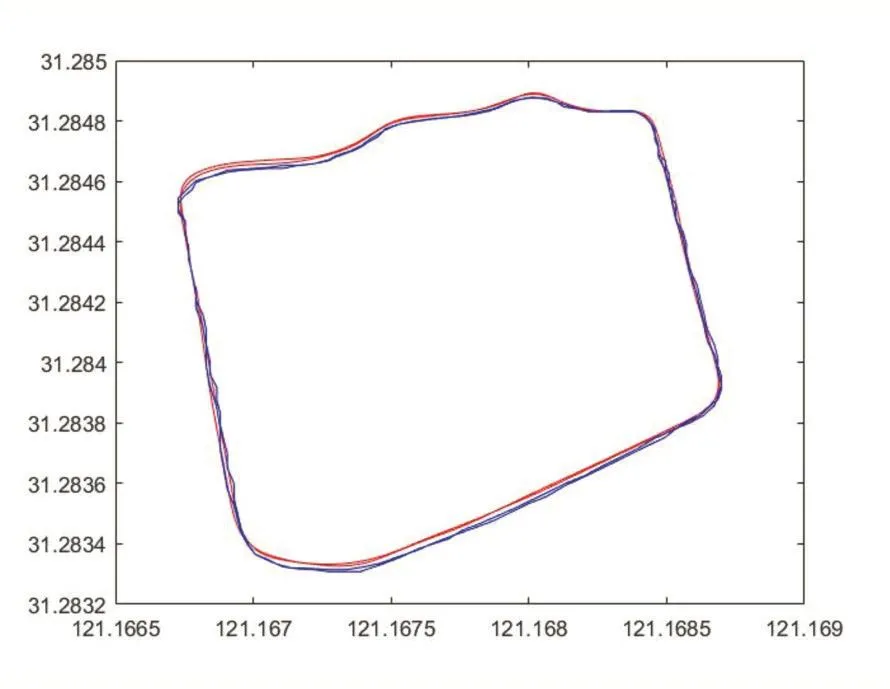
图6 捷联惯导推算路径和GPS实际轨迹

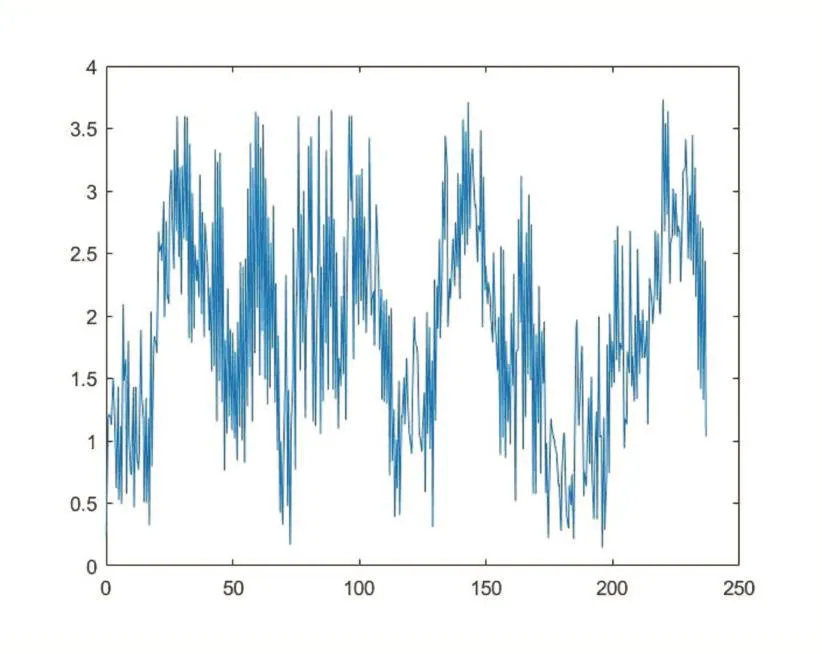
图7 捷联惯导推算路径与GPS实际轨迹的绝对误差

图7中，x轴为测试时间，单位为秒,y轴为捷联惯导推算路径与GPS实际轨迹的绝对误,单位为米。可以看到在运行的3分钟内，绝对误差并没出现超过3.5米的情况，验证了算法的准确性。