基于理解的信息技术深度教学思考与设计
刘鸣家
目前的信息技术课堂,形式越来越多样,活动越来越丰富,如游戏式教学、小组合作、自主探究、竞赛比拼……这些活动都是取外力协助的策略,以活动调动非智力因素,帮助学生建构知识技能。那么,取之于内的策略呢?如何通过更多的智力活动来帮助学生实现理解呢?教什么比怎么教更重要,方向重于方法,内容决定形式,在教学内容和教材挖掘上下功夫,這正是求之于内的策略。信息技术教师精通各类软件操作,面对问题总是随便动动手便可解决,然而解决问题之道真是自然浮现在我们脑中的吗?核心素养中的计算思维讲求解决问题的一系列思维活动,周以真教授也提出计算思维中包括抽象、分解、建模等要素。教师要认定答案不是自然浮现的,自有其来龙去脉,通过拷问内心式的追问,探寻自己的思维过程,寻求对知识技能的更深层理解,才能得以拓展教学设计思路,才能引导学生理解。下面,我结合初中信息技术教材中电子表格部分的两处内容(地址引用与图表创建),谈一谈具体的设计与做法。
● 从顺序到逆推的教学目标设定
以《图表创建》一课为例,有的教师在课后和我交流:24小时空气质量数据表一定要用折线图来表示?本课的常规教学目标是知道图表的类型、掌握创建方法、知道表图关联。以上述教学目标来组织教学,因为数据与时间相关,为表现变化趋势,自然是用折线图。而在我的公开课中,学生面对同一表格,最多呈现了七张图,区别在哪里?因为我的目标设定是用图表表达思想。我的思维过程是假设学生真正理解了图表,那么,我期望他们是根据任务要求完成图表创建,还是根据表格绘制多张图表进行数据分析呢?很显然,如果学生真正理解了,那么我们期待的是后者。基于这一结果预期,我开始追问自己:
一表多图,学生需要做什么?——选数据,建图表。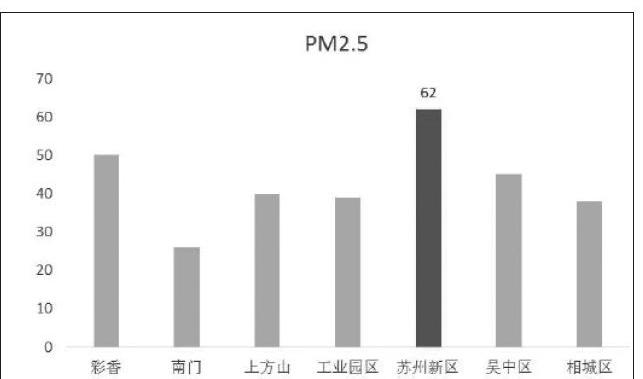
为什么选数据可以建立不同的图表?——因为数据源不同,图表自然不同。
为什么要选择不同的数据源?——因为想要表达的内容不同。
图表是一种表达形式,因需要合理表达,所以需要选择合适的图表类型。那么,在教学目标设定时,关注表达需求应是一切目标的起点,这样的目标设定,才更符合学科核心素养,才能提高信息意识,为解决问题服务。图表的学习是为了能更好地解决表达的问题,不同的表达需要不同的数据,不同的表达需要不同的图表类型。
● 从多杯到一缸的教师思维深度
“与人一杯水,自有一缸水。”这是对教师的学科专业要求。此处的一缸水不只是简单的多少问题,而是包括深度和广度两个方面。通过访谈多位一线教师,我发现,在对教材和所授内容的理解上,教师更多的类似拥有多杯水,广度有余而深度不足。以苏科版初中信息技术7年级教材为例,其中关于图表和地址相对引用的说明如下。
图表的作用:“我们通常难以记住一连串数字,以及它们之间的关系和变化趋势,但可以轻松地记住一幅图画或者一条曲线。……数据转换为对应的图示,更直观的方式显示数据……”
地址相对引用:“计算式中直接用到了单元格地址B8和C8,这就是单元格地址的引用。……可见,通过填充柄填充数据时,只是复制了其中的运算关系,单元格地址做了自动调整,这就是单元格地址的相对引用。”
接受访谈的教师大多理解,图表形象直观,易于记忆;相对地址引用就是普通单元格地址做填充拖拉的时候会自动改变。基于这样的理解,教师进行授课后就出现如文章开头所说,学生在课堂上证明掌握了技能,却在面对新的问题场景时无能为力,迁移并未形成,理解并未真正发生。针对这一情况,我对这两个概念的界定进行了基于更深层次理解的设计。
1.抽丝剥茧,追本溯源
比较法是在进行这一部分教学时教师常用的策略,将文本、表格、图表进行对比,得出图表形象直观、易于记忆的特性,在这一点上,教材、教师、学生的理解层级一致。如果教师更深一层会怎样呢?从表达的角度(借助信息的概念)来看,文本表达了全部的信息;表格剥离了大量的文本信息,保留了必要的字段和数字信息(如表1);图表剥离了大部分的数据信息,保留了PM2.5和监测点信息(如下图)。通过这样抽丝剥茧,我们发现图表保留的信息量远小于文本和表格,那么易于记忆和表达突出是必然的效果。
文本呈现:
为检测空气质量,苏州市设立了7个空气质量监测点,检测包括AQI、PM2.5、PM10等八项数据。
某日,苏州市南门检测点测到的PM2.5的数据是26,相城区监测点监测到的数据是38,工业园区监测点的数据是39,上方山的数据是40,吴中区的数据是45,彩香的数据是50……
当理解进入这一层次,如何制作图表已不重要,重要的是需要保留的数据与表达的含义。此时我完成了自己的深层理解建构,也切合到前文设定的教学目标,摆在我面前的设计之路将比以往更加宽广。
2.咬文嚼字,立足生活
地址引用同样是学生理解的难点,教材、教师、学生的理解层级也是惊人一致,有$的地址引用叫绝对地址,填充时不变,无$的地址引用叫相对地址,填充时自动改变。当然这样生硬的概念谈不上理解,也无法指导学生灵活运用。在此处,我对名词进行咬文嚼字式的理解,并尝试回归生活寻求问题的本源,请看下页表2。
相对在物理学中有明确概念,相对的关键是参照物。相对地址A1:对于B1来说,别称是“左1”,对于C1来说,别称是“左2”。这样一转换,发现和平时我们提的问题是一致的(请在总分一栏计算左边三格之和),地址的相对性自然就凸显出来。相对的参照物是引用单元格、利用地址加别称来找到相对性。同理可以尝试去理解国际象棋问题、杨辉三角问题。基于这样的理解,在公式函数被复制、拖拉填充时的地址变化就一目了然了。基于这样的理解,课堂上学生可以练习和思考的东西更多了,设计之路再次被拓展。
● 从单一到开放的教学环节设计
当我们立足教材,以学生理解预期逆推教学目标,以教师深层理解深挖教材之后,就可以更有底气回答第一部分中的問题:如果学生理解了,那么他们能做什么?教师和学生的深层理解给教与学带来了多样化的选择,理解给了我们选择的力量。理解技术,教师思路将得到拓展,产生更多的选择,由单一方向的命题成为多角度发散性的命题。理解技术,学生思路将得到拓展,在面对开放性试题的时候,有更多的想法和选择。在《为未知而教,为未来而学》中,戴维·珀金斯这样描述:学习即理解,理解即思考。前文我们也提过,理解真正发生的标志是迁移运用的产生,即学生会拥有选择的能力。在面临真实问题和项目时,学生面临的挑战更多的是选择工具,并不断转化问题。现在我们还是回到图表和地址引用的例子上来,看看发生理解后可以做的学生练习设计。
1.教师:设计问题从单一到多样开放
练习设计:将E3单元格(=E2+E4+D3+F3)复制到G7,它的公式会变成什么?你还可以自己设计几个类似这样有趣的问题?
理解:这个公式计算的是E3单元格上下左右四个单元格的和,那么到了G7公式自然会变成……类似的问题本质在于相对性,我也可以这样设计……
原有课堂的练习基本集中在利用填充柄进行横向和纵向的拖动,实现公式的复制。运用相对性来理解地址引用以后,则可以进行公式远距离、跨表复制的命题。比如累计和小计,比如国际象棋问题,理解的不是字符和地址,而是穿越地址直达公式的意义。此时地址的概念是在运用,所谓的公式也回归本真。正如我们说s=vt的时候,其实我们想表达的是路程=速度×时间。而由学生来设计问题,经由他们对问题的天马行空的联想,对语句的反复推敲,进一步加深他们的理解。
2.学生:面对问题的多元开放思考
练习设计:吴江某地24小时空气质量跟踪表,用什么图来进行表达展示比较合适?在什么情况下可以用柱形图呢?可以用饼图展示其中的一些数据吗?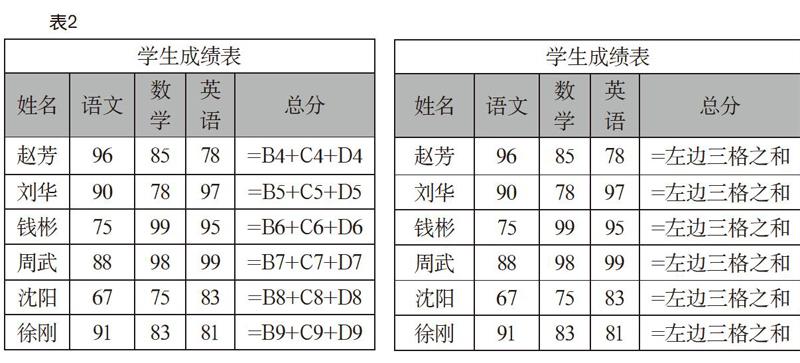
理解:图是为了表达,柱形图比较数值大小,选择表中的2~3个数据,用柱形图就非常合适了。
原先的命题是要求反映数据关系,寻找变化规律。如果理解不够深入,那么学生一般就是套用。先是全部数据的选定,或者两列数据的选定,然后固定化地产生比大小柱形、看变化折线、现比例饼图的思维。在理解为何图更具力量的基础上,选择数据将更灵活,目的从制作图真正转化为用图表达,以图说话,锻炼了逆向思维,以终定始。比如常见的天气变化折线图,如果确定结果需要的是柱形图,需要选择哪些数据,反映何种关系。这里我们用“如果”一词来引导学生逆向思维的产生,进而推动他们对“数据是图的基础,图是数据的表达”这一观点的更深层理解,明白最终数据和图都是为观点服务。
当学生遗忘了我们传授的东西以后,当学生遗忘了我们传授的一步步的操作以后,他们还留下什么呢?我想应该是理解,应该是学生建构出来的,关于问题解决,关于技能本身的理解,专属于学生自身的理解。这份理解将帮助他们日后需要的时候重拾记忆,快速上手,并帮助他们将这份技能迁移到不同的工作环境中,这份理解才是激发、激活他们创造力的源泉。

