密度峰值快速聚类算法优化研究

王鹏飞，杨余旺，柯亚琪

(1.南京理工大学计算机科学与工程学院,江苏 南京 210094; 2.南京农业大学园艺学院，江苏 南京 210095)

1 引言

近年来随着数据的不断增长和累积，如何从这些大数据中挖掘出有用的信息成为了当前的研究热点，聚类就是一种能够从大数据中挖掘出有用信息的有效方法[1]。聚类是聚类分析的简称，是一种无监督的学习过程[2]。聚类是在无先验认知的条件下，根据发现的数据对象的相似性，将对象分组，从而达到对数据的深刻理解，获得有用信息或者压缩数据的目的[3,4]。

聚类分析现在已经应用于诸多领域，如：数据库知识发现、计算机视觉、图像处理、生物信息学等[5]。正因为聚类分析的实用性，许多聚类算法已经被人们提出，其中比较经典的有K-means算法、模糊C-means算法、具有噪声的基于密度的聚类方法DBSCAN(Density-Based Spatial Clustering of Applications with Noise)算法等，近几年又提出了近邻传播AP(Affinity Propagation)算法和CFSFDP(Clustering by Fast Search and Find of Density Peaks)算法[6]。这些聚类算法都旨在解决不同情况下的大数据聚类问题。K-means算法是一种基于距离的迭代式算法，其旨在将数据点划分到距离最近的聚类中心所在的簇中，但K-means算法需要提前指定聚类中心的个数，且对于非球形的数据集很难取得令人满意的聚类结果[7]。基于数据点的密度进行聚类的算法，如经典的DBSCAN算法，则摆脱了对数据集形状要求的束缚，它可以得到任意形状的类簇。DBSCAN算法需选择一个密度阈值，密度高于该阈值的点则成为“核心点”，之后将所有“密度相连”的点聚合为一个类[8]。DBSCAN算法不需要事先确定聚类中心的个数，且能够很好地排除噪声点和离群点。但是，该算法对于密度分布不均匀的数据集所取得的效果并不理想，且该算法最终的结果对所选择的密度阈值十分敏感，这使得对于密度阈值的选择有一定的困难。除了上述两个问题外，DBSCAN算法的计算复杂度也很高，这也导致它很难运用于高维数据环境[9]。

Rodriguez等人[10]于2014年在《Science》上提出了一种基于密度峰值的空间聚类算法，该算法可以对任何无规则的数据集进行聚类[11]。快速寻找密度极点聚类算法CFSFDP算法首先通过使用一截断距离来计算每个点的局部密度，然后计算各数据点与局部密度高于它们的数据点之间的最小距离；然后根据计算出的每个点的局部密度和最小距离绘制决策图，接着在决策图中人工选取聚类的中心，之后将剩余的非聚类中心的数据点划分到与之距离最近的聚类中心所在的簇中；最后再将所得到的各个簇划分为簇核心和簇光晕，从而得到最终的聚类结果。使用CFSFDP算法进行聚类时只需要计算一次距离，并且不需要进行迭代，因此算法的计算速度很快。但是，该算法选择聚类中心的时候需要在决策图中人工选取，这增加了算法的冗余性，不利于算法的自动化，且在最后将簇划分为簇核心和簇光晕时会将簇边缘的本属于簇核心的一些点划分到簇光晕中，影响最终的聚类效果。

针对CFSFDP算法上述两个不足点，本文引入了一种聚类中心的自动选择策略，通过使用异常检测的思想自动计算得到数据集的聚类中心，从而避免了CFSFDP算法需要在决策图中人工选择聚类中心，影响算法自动化的问题。并且在得到初步的聚类结果后进行簇核心和簇光晕的划分时，引入了簇内局部密度的概念，改进了CFSFDP算法原本的划分方法，使得簇核心和簇光晕点划分结果更为合理。实验结果表明，本文提出的算法可以有效地提高CFSFDP算法的自动化程度，并且最终得到的聚类结果与CFSFDP算法相比更为准确合理。

2 CFSFDP算法

CFSFDP算法进行聚类时首先需要确定类的中心点，其假设簇的聚类中心的局部密度高于其周围数据点的局部密度，并且聚类中心与那些局部密度更高的数据点之间的距离较大。对于一个给定的数据集，CFSFDP算法需要为每个数据点计算两个量化值：数据点的局部密度ρi和它与局部密度比其高的数据点之间的距离δi。

数据点xi的局部密度ρi有两种计算方式：基于截断核的计算方式和基于高斯核的计算方式。使用截断核计算局部密度ρi的公式为:

χ(δij-dc)

(1)

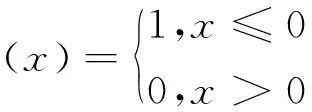
使用高斯核计算局部密度ρi的公式为:

(2)

其中,δij为数据点之间的距离，Is为i的值域，dc为截断距离即距离阈值。使用该计算方式得到的局部密度ρi仍然满足与数据点xi的距离小于dc的点越多，局部密度ρi就越大的结论。使用截断核计算局部密度和使用高斯核计算局部密度这两种计算方式的区别在于使用截断核计算得到的结果为离散值而使用高斯核计算得到的结果为连续值。因此，相对而言，使用高斯核计算得到的数据点具有相同的局部密度的概率比使用截断核计算得到的数据点具有相同的局部密度的概率要小，使用高斯核计算局部密度ρi更方便比较数据点局部密度之间的大小关系。

数据点之间的距离δi是通过计算数据点xi与比该数据点局部密度高的其他数据点的距离得到的，数据点之间的距离δi可以根据公式(3)计算得到。

(3)

一般而言，数据点之间的距离δi为数据点i与比该数据点局部密度ρi更高的其他数据点的所有距离中的最小值，但对于局部密度ρi最高的点，数据点之间的距离δi为其他数据点与之距离的最大值。

CFSFDP算法根据数据点之间的距离δi与数据点的局部密度ρi的各自的大小关系绘制决策图，通过在决策图中人工选取簇的聚类中心，其决策图如图1所示。算法将δi值大且ρi值较大的点认定为簇的聚类中心，即在决策图中处于右上角与其他点分离明显的部分点。在确定簇的聚类中心之后，便将其他剩余的数据点划分到局部密度比其高且与之距离最近的聚类中心所在的簇中。

Figure 1 Decision graph of CFSFDP图1 CFSFDP算法决策图

CFSFDP算法不同于DBSCAN等聚类算法，其对于较低密度的簇类点没有引入噪声的概念，而是为每一个簇引入了一个光晕的概念，簇的光晕中则包含了其他算法中所定义的噪声以及数据集中的离散点。CFSFDP算法将一个簇划分为簇核心和簇光晕，属于簇核心中的数据点的局部密度ρi较大，而属于簇光晕中的数据点的局部密度ρi较小，局部密度ρi较小的点则包含了簇的噪声点以及数据集的离散点。为了划分簇的簇核心与簇光晕，CFSFDP算法引入了“边界区域”的概念，它的定义为：数据点属于该簇，但在与该数据点的距离小于dc的范围内存在属于其他簇的数据点，由这些点构成的区域范围称为该簇的“边界区域”。在取得每个簇的“边界区域”后，将“边界区域”中局部密度最大的点的局部密度值作为该簇的簇核心与簇光晕的分割阈值ρb。最后根据该簇中的数据点的局部密度ρi与该簇的密度阈值ρb的关系将该簇数据点划分到簇核心或者簇光晕中，若该簇内的数据点的局部密度ρi大于ρb，则该数据点划分到该簇的簇核心中，否则将其划分到该簇的簇光晕中。经过将各簇进行簇核心与簇光晕的划分之后便得到了CFSFDP算法最终的聚类结果。

3 CFSFDP算法改进

CFSFDP算法在选择聚类中心时需要人工辅助选择，选择方式为在决策图中，将右上角的点作为起点，向左下方拉矩形，利用矩形框选择与其它点差异最大的一组点，该组点即为聚类中心。该过程因为需要人工参与，使得算法的冗余性增加，并且人工选择具有一定的主观性，选择结果的不同将会影响最终聚类的结果，这不利于最终结果的准确性以及算法的自动化。除此之外，CFSFDP算法在划分簇核心和簇光晕时，会将一些处于簇边缘的数据点划分到簇光晕中，使得最终得到的聚类结果的准确性降低。本节针对CFSFDP算法上述两个不足点提出了优化方案，使得算法可以自动选择聚类中心且对于簇核心与簇光晕的划分更为合理，从而获得更合理的聚类效果。

3.1 聚类中心的自动选择

通过对CFSFDP算法的介绍可知，CFSFDP算法有两个基本立足点：

(1)聚类中心的局部密度很大。

(2)聚类中心与其他局部密度更大的数据点之间的距离相对较大。

根据这两个基本立足点可知，聚类中心的局部密度ρi和与局部密度比其高的数据点之间的距离δi这两个值都是比较大的。鉴于此，本文提出的聚类中心自动选择的策略为：使用标准化的局部密度ρi和相邻距离δi的乘积来评测聚类点之间的差异度，然后对于该乘积使用高斯分布进行异常检测的方法得出其中的异常点，对于需要进行聚类的数据集而言，这些异常点即为聚类中心。高斯分布是非常适合做异常检测的一个模型，分布在两端的小概率事件可认为是异常点，利用这一点可以得到数据集的聚类中心。

首先引入一个簇中心权值的概念，定义一个数据点的簇中心权值γi为:

(4)

(5)

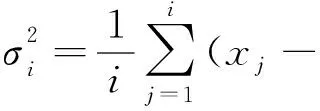
(6)

接着对于每个γi，根据公式(7)分别计算它们各自的概率密度。

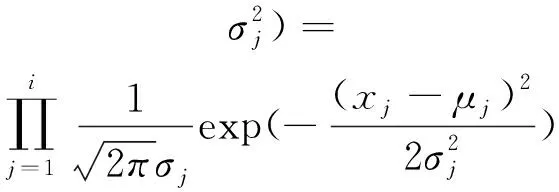
(7)

最后根据p(γi)与给定的一个阈值ε的关系来判断数据点是否为异常点即聚类中心，ε为一个较小的常数，本文选取的阈值为0.005。对于交叉验证集可以尝试多个ε，并基于该ε计算交叉验证集上的F1值，取最高者返回。F1的定义如下：

(8)

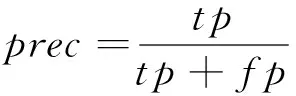
Figure 2 3-spiral dataset图2 三螺旋数据集

Figure 3 Clustering center obtained from anomaly detection图3 异常检测所得的聚类中心图

算法1给出了聚类过程中簇的聚类中心自动选择的具体步骤。

算法1聚类中心自动选择策略

步骤1将每个数据点的局部密度ρi和数据点间的距离δi标准化。

步骤2求取每个点的簇中心权值γi。

步骤4求取每个点的概率密度p(γi)。

步骤5判断p(γi)与阈值ε的大小关系，若满足p(γi)<ε，则该数据点为簇中心，否则不是聚类中心。

3.2 簇核心与簇光晕的分割优化

χ(διj-dc),ci=cj

(9)

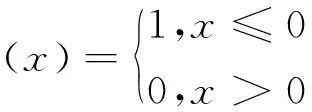
算法2给出了在得到初步的聚类结果后，所得到的簇的簇核心与簇光晕分割的具体步骤。

算法2簇核心与簇光晕分割策略

步骤1确定簇的“边界区域”。

步骤2求取“边界区域”内每个数据点的簇内局部密度。

步骤3计算“边界区域”的平均簇内局部密度。

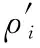
Figure 4 Three types of classical datasets图4 三种典型的数据集

4 仿真实验

为了表明本文所提算法的有效性，使用Matlab进行数据仿真得到聚类结果。选用三个具有代表性的数据集：数据集1来自文献[13]，是一组模拟的二维数据集，如图4a所示，共有788个数据点，该数据集的数据分布较为密集，各区域间的分隔较为明显，一般该数据集根据数据点的聚集情况被划分为7类；数据集2来自文献[14]，是一组由15个相似的二维高斯分布组成的模拟数据集，如图4b所示，共有600个数据点，该数据集中，四周的数据分布较为稀疏，中间部分的数据分布较为密集且各区域之间粘连较多，一般该数据集根据数据点的聚集情况被划分为15类；数据集3是一组选自Olivetti人脸数据集(Olivetti Face Database)中的部分图像，图中每一行为同一个人的不同表情的图像，同一个人的不同图像之间有细微的差别，是一组真实的数据集，如图4c所示。

图5为使用原始CFSFDP算法对数据集1和数据集2进行聚类时得到的决策图，图中灰色的点为人工选择得出的数据集的聚类中心，点的个数即为数据集聚类时类的个数，这些点是多次人工选择聚类中心进行实验后选出的最为合理的聚类中心点。图6为使用本文所提出的异常检测方法所得到的数据集中的聚类中心，图中灰色的点为算法自动计算得出的聚类中心。

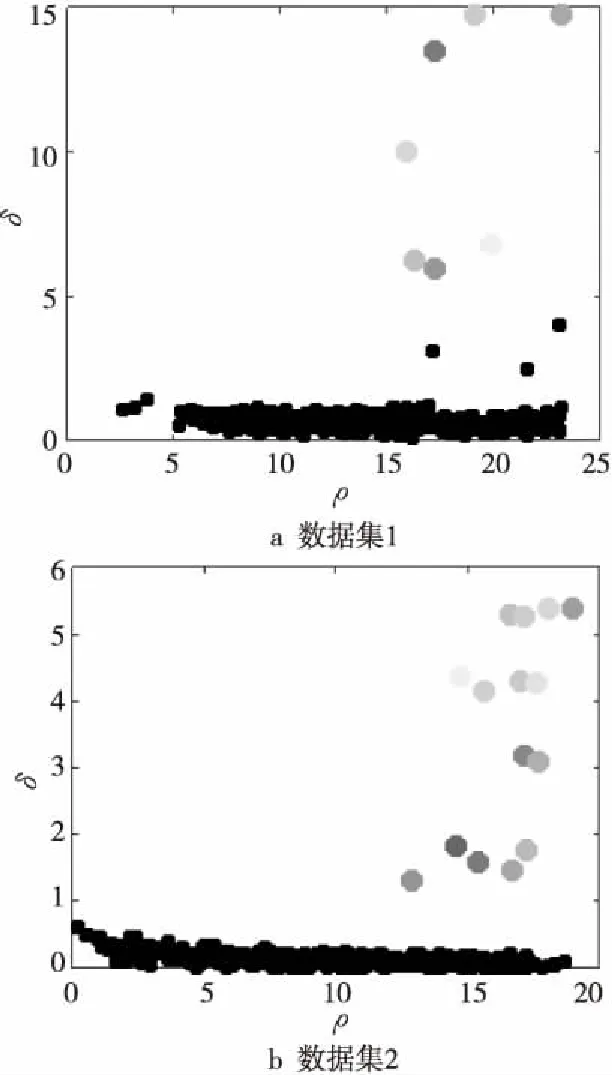
Figure 5 Decision graphs obtained by CFSFDP图5 利用原始CFSFDP算法获得的决策图

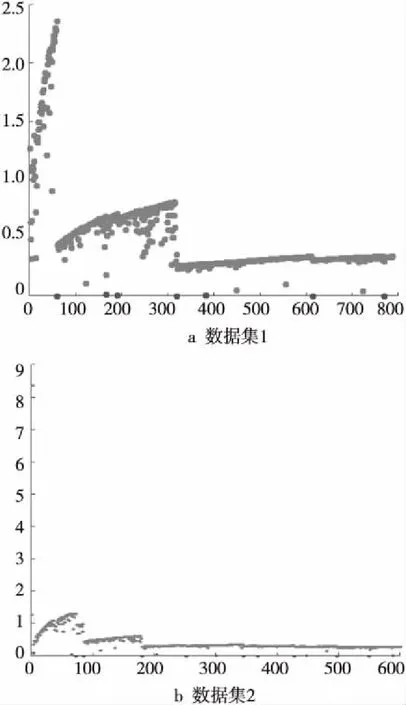
Figure 6 Clustering center obtained from improved CFSFDP anomaly detection图6 改进的CFSFDP算法异常检测得到的聚类中心图

Figure 7 Comparison of decision graph and anomaly detection of datasets 1图7 数据集1决策图法与异常检测法实验结果对比

Figure 8 Experimental result comparison between decision graph and anomaly detection of datasets 2图8 数据集2决策图法与异常检测法实验结果对比

图7和图8为对数据集1和数据集2使用CFSFDP决策图方法得到的聚类结果与使用改进的CFSFDP算法的异常检测方法得到的聚类结果，图中每种灰度代表一个簇，黑色的点则为各簇的簇光晕部分。图7和图8中使用异常检测法得到的聚类结果中，簇核心与簇光晕的划分使用的是原始CFSFDP算法中簇核心与簇光晕的划分方法。从图7和图8对比可以看出，使用改进的常检测方法得到的聚类结果与使用原始决策图法得到的聚类结果完全相同，这表明使用改进的CFSFDP算法得到的聚类中心较为准确，可以代替使用原始CFSFDP算法的决策图法人工选择聚类中心，实现对CFSFDP算法的进一步自动化。

在得到初步的聚类结果后，对得到的簇进行簇核心与簇光晕分割优化后的实验结果如图9所示，图中黑色的点为分割后的簇的簇光晕部分。通过图9a与图7a的对比以及图9b与图8a的对比可以看出，使用本文提出的簇核心与簇光晕优化分割方法得到的实验结果，将簇的边缘部分本属于簇核心部分的数据点划入簇光晕中的几率变小，只有簇之间粘连部分的数据点以及数据集中的离散点被划入了簇光晕中，得到的最终实验结果与CFSFDP算法得到的实验结果相比更为合理。

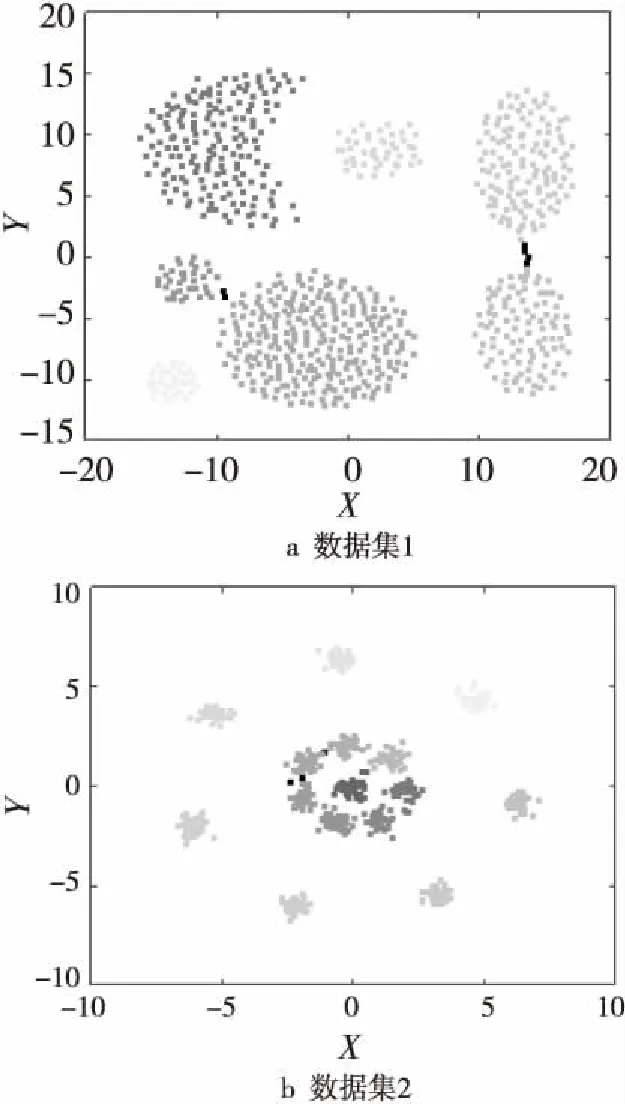
Figure 9 Division optimization results of cluster core and cluster halo图9 簇核心与簇光晕分割优化实验结果图

图10为对数据集3的Olivetti人脸数据集聚类后的结果，图10a为使用CFSFDP算法得到的聚类结果，图10b为使用本文改进的CFSFDP算法得到的聚类结果。图10中的人脸小图的右上角使用圆点标记的为算法所选择的聚类中心，人脸小图左下角的每种小图标代表一个簇，左下角未被小图标标记的人脸小图则不属于任何一个簇。从实验结果可以看出，本文改进的CFSFDP算法自动选取的聚类中心与原始CFSFDP算法人工选取的聚类中心相同，从聚类的结果来看本文改进的方法略优于原始的CFSFDP算法。

Figure 10 Clustering result comparison between CFSFDP and the optimized CFSFDP 图10 原始CFSFDP算法与本文改进的CFSFDP算法对Olivetti人脸数据集进行聚类的实验结果图

从上述对比实验可以看出，本文提出的方法可以有效地提高CFSFDP算法的自动化程度，且聚类效果更准确有效。

5 结束语

本文提出的算法是对CFSFDP算法的两点不足进行的优化改进。针对CFSFDP算法需要在决策图中人工选择聚类中心，导致算法的准确性和自动化受到影响，本文采用改进的CFSFDP算法的异常检测方法自动计算出聚类中心，针对CFSFDP算法最后进行簇核心与簇光晕分割时会将簇的边缘数据点划入簇光晕中，影响实验结果，本文通过引入簇内局部密度，根据簇内数据点的局部密度与簇内局部密度的平均值的关系划分簇核心和簇光晕。仿真实验对比结果表明，本文提出的算法是有效可行的，其实验结果比原始CFSFDP算法的实验结果更为准确合理。