专题复习要举一反三

于爱文 盛建武

鉴于中考数学压轴题的综合性、阶梯性与难突破性，初中数学专题复习至关重要，例题的选择与讲解的效果直接影响学生应用数学知识的能力。因此，初中数学专题复习的例题选择与讲解更应该注意相应的技巧和策略，让学生能够充分地吸收例题中蕴含的解题思路和方法，实现从教知识向教方法、思想的转变，让学生通过专题复习优化自己在该专题的知识结构。那么，在数学专题复习中，如何真正做到举一反三，实现学生在知识、能力、情感态度、经验积累的全面提升？我们以“二次函数的面积问题”为例，从数学核心素养角度出发，创新教学设计，探究了有效的数学专题复习教学策略。

一、原教学设计简述

环节1.自主研学

如图1，在平面直角坐标系中，已知抛物线P的顶点M（1，4），且与x轴交于A，B两点，与y轴交于点C（0，3）。

问题1：求出抛物线P及直线BC的解析式；

问题2：设抛物线P的对称轴与BC相交于点D，求出线段BC与线段 MD的长度；

问题3：连接MC，MB，求出吟MCB的面积。

环节2.合作探学

问题4：设E点是抛物线P上第一象限的动点，连接EB，EC，当吟ECB的面积最大时，求出E点的坐标及面积的最大值。

变式1：设E点是抛物线P上第一象限的动点，连接EB，EC，当四边形OBEC的面积最大时，求出E点的坐标。

环节3.拓展研学

环节4.总结思学

请从数学解题思想与应用到的数学方法方面小结。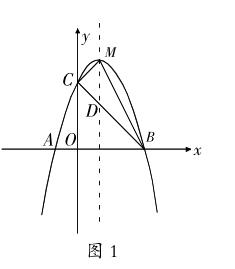

点评：1.在教学目标的设计上，力求通过学生的探究，将二次函数与三角形、四边形、相似等知识融合在一起，构建它们之间的联系，形成关于二次函数的面积问题的新的认知结构，从而优化学生的认知结构。但在实际教学过程中，一次抛出三个问题，对于学生来说难度较大，环节1花的时间比较多，且效果不佳，大多数学生无从下手，学习积极性不高，思维未被激活。这主要是教师过高地估计了学生的认知和思维发展水平，教学脱离了学生的实际。

2.本节复习课的重点是学生在解决二次函数的面积问题的过程中，体会转化的数学思想。转化的数学思想可以化难为易、化隐为显、化繁为简、化曲为直，从而让学生较容易地建立未知与已知之间的联系，构建数学模型，解决数学问题。本次复习的具体转化的策略是水平分割与竖直分割，化隐为显，建立二次函数与三角形、四边形面积之间的联系。但在教学过程中，呈现的方式与呈现的层次性不够，导致学生尽管能掌握这一问题的解答，但对于转化的数学思想体验不够，经验积累不足，目标达成大打折扣。

二、改进后的教学设计

基于以上思考，为了突破难点，有效地实现本专题的复习目标，我们对本节数学专题复习课重新进行了设计，修改如下：

如图2，在平面直角坐标系中，抛物线P的顶点M（1，4），且与x轴交于A，B两点，与y轴交于点C，其中B（3，0）。

问题1：求出抛物线P的解析式。

点评：在初中数学学业水平考试中，求解抛物线解析式是经常考查的问题，大部分学生仅局限于用抛物线的一般式进行计算求解，而一般式涉及解三元一次方程组，不仅式子复杂，运算量也大；不但容易出错，而且浪费时间，因而选择一种简便的解析式和计算途径至关重要。本题的设计，出于优化学生解题策略的考虑，让学生根据解析式的问题特征，选择用顶点式y=a（x-h）2+k进行求解。因为使用顶点式求解，代入顶点坐标后，仅需解一个一元一次方程，大大简化了计算。这样，学生解决问题的思维方式更合理。

将题目的原设计C（0，3）改为B（3，0），原设计仅让学生体会顶点式的应用，二次函数的交点式则没有覆盖到位，而修改后不仅可以使用顶点式，也可使用交点式求解。

追问：除了使用顶点式求解，还能使用其他方法吗？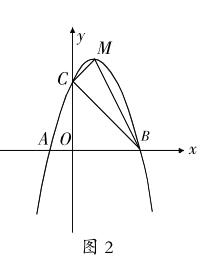

点评：学生除了可以用顶点式和交点式求解外，在得到A（-1，0），B（3，0），M（1，4）之后，也可以使用一般式，使得解题策略多样化，不仅激发了学生学习积极性，也激活了学生思维。

问题2：连接MC，MB，求出吟BOC与吟MCB的面积。

点评：有关求解三角形面积类型的题，极少出现特别直观的面积求解问题，很多时候需要进行转化。转化采用得最多的方法是分割（即水平分割与竖直分割），而△MCB的面积求解很好地展示了这一数学思想方法。

问题3：在原问题4的基础上，增加一步变式。

追问：在抛物线P上第一象限内求点E，使点E到线段BC的距离最大，求出最大值。

点评：本问题设计的核心思想是转化思想，将△EBC的面积最值问题转化为求线段EG的最值问题，以及在问题2的基础上对三角形的面积求法做具体的应用。

问题4：在原问题5的基础上增加2问变式。

点评：本问题设计涉及取值问题，进而引发更深层次问题，求k的取值范围。学生不仅思维能更上一个台阶，解决问题的能力也会得到提高。

总评：本教学设计对专题复习课的教学作了整体设计，已经实现了由教知识向教方法、思想过渡。一是从学生整体发展出发设计教学目标，而不是只考虑中考的近期目标，特别注意学生在解题过程中对数学思想与方法的掌握。数学思想与方法是数学大厦的基石，是数学解题的灵魂。它来源于数学基础知识，又反过来指导学生运用数学知识和方法解决问题。所以在平时的训练与例题讲解中，要结合具体问题理解和掌握数形结合、分类讨论、函数方程、数学建模等常见的数学思想与方法。二是根据学生的特点进行内容的整体安排，内容选择要精，教师通过多个问题，将二次函数的面积问题逐层分解，步步紧逼，直达问题的核心，让不同的学生在学习中都有所收获，有所体验，每位学生都有发展。三是教学方法上既充分发挥学生的主体作用，又发挥教师的主导作用，让学生运用数学知识解决数学问题的过程，重视解题方法和解题规律的总结和提高。

本专题复习教学设计，提高了学生的各种数学能力。纵观《数学课程标准》中对能力的考查，大致可分成两个阶段、两个层次。一个阶段是以考查运算能力、空间想象能力和邏辑思维能力以及分析和解决纯数学问题的能力为特点的阶段。在此基础上，近年来又强化了阅读理解能力、探索创新能力和数学应用能力，以及建立在此基础上的作为数学核心能力的思维能力。特别是把数学作为文化和培养人的一个不可分割的整体中的一个部分时，对学生的情感、意志、毅力、价值观等非智力因素的考查，就必然会进入一个新的阶段。初中数学学业水平考试，突出对学生思维能力与数学意识的考查，进而落实《数学课程标准》中关注学生思维能力和数学意识的培养目标，激发学生的发展潜能。本专题的设计将二次函数融入面积计算之中，将二次函数、三角形、四边形和相似等知识有机结合，提升学生的认知能力，并将转化思想、函数思想、方程思想渗透其中，让学生在数学思维、数学感悟、数学情感、数学积累上有较大的发展。

本专题复习教学设计还为我们提供了以下经验和方法：变更数学题目的表达形式和背景，培养思维的深刻性。寻求不同解题途径与思维方式，培养思维的广阔性。对问题解答的思维方式不同，产生解题方法各异。这样的训练将有益于打破思维定式，优化解题方法，从而培养发散思维能力。变换几何图形的位置、形状和大小，培养思维的灵活性、敏捷性。注意把课本中的例习题多层次变换，这样既加强了知识间的联系，又激发了学生学习的兴趣，达到了巩固知识又培养能力的目的。改变题目的条件和结论，培养思维的批判性。这样的训练可以克服我们静止地、孤立地看问题的习惯，促进我们对数学思想与方法的再认识，培养研究和探索问题的能力。

（作者单位：长沙市北雅中学长沙市开福区教育科研培训中心）