活用教材 向学生思维更深处漫溯

杨文婷

漫，表示没有限制，没有约束。溯，代表逆流而上。徐志摩在《再别康桥》中随心而上，“向青草更青处漫溯”，终究“满载一船星辉，在星辉斑斓里放歌”。然而，在有些数学课堂中，教学内容单一、各知识点缺乏系统性，有的甚至与中学严重脱节，始终无法触及学生的思维深处，学生的思维总是被动地跟着老师走。那么，我们是不是也应该如徐志摩般，挣脱过多的约束和限制，撑一支长篙，向学生思维更深处漫溯？

寻觅———学生的思维深在何处

培养学生的问题意识，从他们的问题中探寻他们的思维方向，是一种有效的策略，很多老师也做了尝试。但是在实施过程中，部分老师由于缺少教学经验，没有发现和掌握教材编排的连贯性，导致学生的思维受到了限制，所提出的问题大多停留于表面，缺乏思维的深度和广度。

如整数运算律在分数中的推广这一内容，有老师抓住交换律和结合律，一步步带着学生观察分数算式中是否存在交换律和结合律，整节课学生都被老师牵着鼻子走，没有自己思考的机会，更谈不上进行深层次的思考。那么，如何将学生的思维引向深入呢？近几年，我们工作室的老师结合人教版小学数学新教材，活用教材，尝试对部分教材进行了整合和改编，让学生感受知识的延伸和扩展，从而举一反三，由此及彼地进行深层次的思考。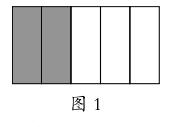

撑篙———在沉淀中促进学生思维的发展

分数的初步认识是人教版三年级上册的内容，按照教材的编排，首先认识几分之一，再认识几分之几，前前后后有5个例题。虽然这5个例题前后联系紧密，但笔者认为并不利于学生对分数进行整体的感知，尤其是知识点造成了学生思维的琐碎，使得新课标中强调的数感的培养难以实现。因此，笔者尝试将教材中的例1至例5组合为一个课时，紧扣平均分，以认识几分之几为切入点，收到了不错的效果。

首先从学生的生活经验入手：一个长方形的蛋糕，有爷爷、奶奶、爸爸、妈妈和妙妙5个人，所以将蛋糕切成了5等份，因为妙妙生日分给了她2份。（如图1）

妙妙好开心啊，她到处跟人说：“我可以吃2个蛋糕啦。”思考：她说得对吗？为什么？她到底吃了多少个呢？

通过这样的处理，学生的思维被拓开。他们发现分数就是先平均分，分成的份数就是分母，取的份数就是分子。从而想到了这样的问题：是不是只有图形平均分才能得到分数呢？学生联想到生活中的分月饼、分西瓜等情形，找到了更广义的分数。课的最后，更有孩子提出了这样的问题：难道只有一个物体平均分才能得到分数吗？教师适时通过课件演示6个苹果装入一个篮子里的过程，让学生感受到，原来一些物体也可以看成一个整体从而得到分数。

整堂课中，学生的思维随着对分数整体的理解，激发出了超强的创造力，带给了我们无限的惊喜！

放歌———在教材与学生已有知识经验的有效整合中达到事半功倍

要做到活用教材，除了理解教材，更重要的是理解学生。万以内数的认识是二年级下册中的教学内容，在此之前，学生已经有认识千以内数的经验，是否还需要从头再来呢？带着疑问，笔者对所教的二年级班级进行了抽样摸底，从两个班中每班选出50%的学生组成“优等生+中等生+学困生”组合。每组学生测试同样的三个问题。第一个问题：4315该怎么读？每个数字各表示什么意思？（检查学生对数位的理解与认识）第二个问题：由8个十、3个百、5个千和6个一组成的数是多少？（特意打乱顺序，进一步检测学生对于数的组成的理解）第三个问题：请从1899数到2000。（检查学生对于数的认知及数感）

笔者从调查的结果中发现，第一个问题的正确率为100%，也就是数数这一关所有学生都没有问题；第二个问题的正确率在90%左右，个别学生因为没有看清楚数位顺序而弄错，但经过提醒后，正确率达到了100%；第三个问题的正确率为85%，部分学生容易在需要进位的地方数错。由此可见，学生对于数位已经有了一定的理解，写数和读数完全不是问题，难点还是在数数以及对大数的感知中。

结合调查，笔者对教材进行了如下调整：1.从生活实际出发，以学生熟悉的价格为依托，以小组活动的形式自主完成万以内数的读数、写数及组成的学习。2.在数数中引入学生已有的知识经验，如图2，遮住每个数的千位，引导学生与原来百以内数的数数方法进行对接。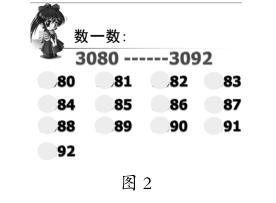

然后重点突破拐弯数，从百位的变化开始，如图3。

最后重点突破需要连续进位的数，以计数器作为辅助，如图4。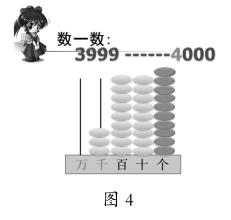

经过这样的调整，教学突出了重点，学生的思维也在原有的基础上得到了发展，可谓是事半功倍。

笔者认为，要漫溯到学生的思维更深处，教师应当灵活地处理教材，挖掘其中的数学本质，找到学生的思维起点，开拓学生的思维方向。换而言之就是，每次處理教材时问自己三个问题：知识的本质是什么？学生的思维起点在哪里？学生的思维发展方向在何处？这样处理，教师才能在与教材、与学生一次次的碰撞中，邂逅学生思维的满船星辉，在星辉斑斓里放声歌唱！

（作者单位：长沙市芙蓉区楚怡学校）