工商银行A股股票虚拟BS期权定价与最优Delta对冲的构造
刘光远


摘要:文章立足于金融期权衍生品构造和对冲的基本方法对现实中工商银行的A股股票进行6个月欧式期权的构造以及对构造的期权进行包含无交易成本、绝对交易成本以及相对交易成本下的最优对冲成本探寻,并在运用广义维纳过程对未来6个月内股价进行合理预测的基础上根据期权的Delta值测算出有交易成本下的平均最优对冲间隔为19.25天。文章通过研究,为今后我国股票期权的构造以及成本的合理对冲提供思路。
关键词:工商银行股票;BS期权定价;Delta对冲
一、引言
(一)研究背景
1. 中国金融市场发展不够全面,金融市场投资标的少,衍生品市场发展滞后。
2. 衍生品产品结构不合理、缺少足够的有价值的期权产品对金融市场的风险进行管理。
3. 具体来说,目前几类有农产品期权和唯一的50ETF交易型基金期权,缺少股票期权。
(二)创新点
1. 中国股票市场发展层次上并不健全,没有多样化的衍生品对股票的风险进行对冲,具体地,中国股票期权市场发展缓慢没有足够的期权对股票投资的风险进行对冲,从衍生品构造的基本理论来构造虚拟期权并进行最优对冲的设计能够结合现实情况,具有前瞻性。
2. 能够为今后中国大类股票的期权的构造及交易策略的设计提供比较有价值的参考意义,该套方法能够在A股具有大市值特征的股票中进行拓展,在该范围内具有一定的泛化能力。
二、策略模型机理阐述
(一)金融期权定价
金融期权是一份未来能够实现买入或卖出某项金融基础资产的权利,由于期权的权利只有权利而没有义务,故为了平衡金融基础资产的买卖双方的利益,就必须对金融期权进行合理的定价使期权的空头方得到多头方一定的对价支付以弥补。常见的期权定价方法有两种:布莱克——斯科尔斯模型(BS模型);二叉树模型。
本文将对中国工商银行A股股票进行欧式期权的构造,故选用BS模型进行计算。其中,BS看涨期权模型具体如下:
本文中c代表工商银行股票看涨期权的价值,S0代表股票在2017年12月8日的收盘价,K为执行价格,r为股票的贴息率,T表示期权的期限,。具体地,N为标准正态分布函数,其分别在d1和d2的条件下计算出看涨期权的价值。
(二)Delta希腊值的测算
期权中的Delta值为定义为期权价格变动与其标的资产价格变动的比率,它是期权价格与标的资产价格变化曲线的切线斜率。在一般情况下期权价值的变动为曲线,故根据定义,Delta值得公式为:
(三)最优Delta对冲
Delta对冲是指期权交易员通过测算Delta值对空头期权后多头基础资产进行回补以控制期权行权风险的措施。假设股票价格为10元,期权的价格为1元,金融机构的交易员卖出了10分该股票看涨期权(有权购买1000股股票),Delta为0.6,则交易员的头寸可以通过购买0.6×1000=600股股票来对冲,即期权头寸上对应的盈利(亏损)可由股票头寸上的亏损(盈利)来抵消。因此期权的交易者为控制自身的风险就必须进行依托于Delta值的反向对冲。一种较为特殊的情形是投资者整体的Delta值为0,即股票头寸的Delta被期权头寸的Delta所抵消,这种情况被称为Delta中性,这时投资者在进行多(空)头期权时就没有必要进行基础资产的反向对冲了。
然而Delta为0在现实中是几乎不可能发生的事情,更加符合现实的是随着时间的变化而不断变化的Delta值,为了进行更加合理的风险对冲就必须在期权期限内不断地进行多次以不同Delta值为基础的对冲操作。这种描述被称为动态对冲。
而最优对冲通常指在动态对冲中使得总的对冲成本最小的对冲策略。一般做法为通过广义维纳过程模拟出期权期限内的股价,从而在设定执行价后计算出分时点的期权价格和对应的Delta动态值,最后计算出反向对冲的成本来进行不同时间间隔策略下的最优规划。
三、数据描述与处理
通过从wind数据库中导出中国工商银行从2014年12月8日到2017年12月8日的日收盘价数据,通过数据的处理,将数据分为6个区间,分别为2014年12月8日至2015年6月7日,等间隔的至 2017年6月8日至2017年12月8日。
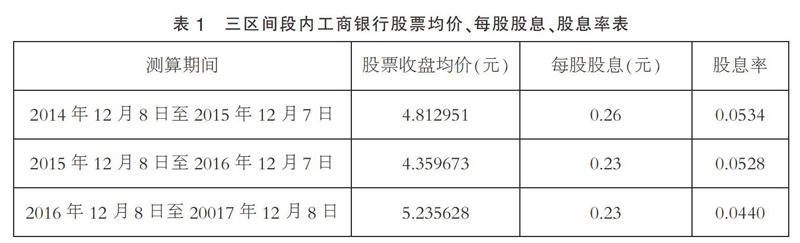
从时间序列上依次对相邻两区间进行均值求解,将半年区间的收盘价转化为年度区间的收盘价均值,得到收盘价、股息和股息率如表1。最后通过对3年历史数据进行再次平均,得到最终的3年历史收益率为12.6821%,无风险利率为5%。而波动率通过由时间的远近将六个区间的标准差数值进行1~6的赋权后平均,波动率为25.51058%。
四、实证结果分析
(一)静态期权价格结果
根据BS模型,将工商银行2017年12月8日股票收盘价5.88元、历史半年期望收益率0.126821、股息率0.05和历史6个月波动率0.2551058以及行权价格6.468元帶入公式,计算得到6个月静态看涨期权的价格为0.2493457元。
(二)无交易成本时动态看涨期权对冲成本计算结果
查询到2017年12月8日中国工商银行的收盘价为5.88元,为计算出未来6个月工商银行看涨期权的合理价格,需要通过三步进行,首先将以上数值带入到公式:
上式中,S(T)代表T时刻工商银行股票的价格,S(0)表示2017年12月8日工商银行收盘价,r为无风险收益率,σ为历史波动率,W(t)为连续时间的维纳过程。
通过不同时间的多次迭代运算,可以计算出服从几何布朗运动的未来6个月股票价格的变动情况,以及未来6个月的Delta值,最终计算出动态看涨期权的价格情况,如图1所示。
从图1第一幅图中可以看出,从时间飘移和随机波动加和股价蒙特卡洛模拟中,未来半年工商银行股票价格将会从5.88元飙升至2个月后的7.75元,之后时间段内围绕7.5元的价格进行上下震荡,其后,Delta值将从0.59快速上升至两个月后的0.97并随着模拟股价的上涨快速逐步震荡上升并在4个月后收敛到1的水平。同样,工商银行看涨期权的价格也与模拟股价的价格相呼应,在从每份0.49元上升至2个月后2元的水平,之后再围绕1.75元的价格轴线上上下波动。
一般来说,加入的基期价格走高,则执行看涨期权的概率也会相应上升,然而要复制该看涨期权就必须买入更多的股票,同时,下降的股价导致更低的Delta,意味着卖出。总体而言,如果股票价格昂贵,策略为买入股票;如果股价低廉,则卖出股票。期权价格源自于这个对冲成本。股价重新平衡期的时间越短,所追踪的价格变动幅度就越小。
John C.Hull定义对冲成本为买入和卖出对冲所需股票的累计净成本的现值。其中全部成本分为两部分:购买股票所需的金额以及保有该头寸的融资利息。在BSM模型中,本文将使用无风险利率进行复利计算,并可以看到对冲成本取决于未来价格的运动,通过模拟工商银行股票价格的路径,可以画出对冲成本的分布状况,发现股票价格更高的波动率会引起对冲成本更高的波动率。
表2中列式了从半日到4周对冲操作频率下的期望成本(E)、成本标准差(v)以及标准差单位期权价格比率(ratio)。可以看出单笔对冲成本在不同的时间调整频度下从每4周0. 5074421元下降到每2天0. 4940984元,但是随着交易频次逐渐增加到每半天一次,则对冲成本会缓慢增加到0.4946613元每笔。但是,随着对冲频次从每4周一次上升到每天2次,总对冲成本的标准差从13.6%显著降到了约2.3%,成本愈加稳定和可期。同时,总对冲成本标准差单位期权价格比率从对应的28.6%降到了4.8%。
然而,一个良好的衍生品对冲策略必须与实际高度的切合,只有如此,该衍生品对冲策略才能够在实际中充分发挥出其理论上所论证的价值。
就上述的中国工商银行假想看涨期权的对冲而言,昂贵的佣金成本即为最优对冲策略的一个限制性条件,如果忽略交易过程中的费用而只是追求没有对冲策略的最优化,则在现实操作中必然会与前期的预想南辕北辙。为了探寻更加符合现实的对冲策略,本文接下来从加入绝对交易成本和相对交易成本两个角度对最优对冲策略进行进一步的探讨,以期寻找出最优的时间操作频次。
(三)加入交易成本后动态看涨期权对冲成本计算结果
表3中所反映的数据均为加入了单笔对冲成本后进行的计算。进行对比后发现在每笔对冲成本0.02元的条件下,总成本将随着对冲频次的升高而单调升高,并在1日两次的对冲中达到0.5433元/笔,而在每笔对冲成本1%的条件下,总成本将先在2周1次的对冲频次下达到最小值(0.0616元/笔)之后最终在每日2次的操作频次下达到0.0807元每笔的最大值。同时,两种成本的标准差也都呈现出一种平稳增加的趋势。
如何在两种交易成本的测度下實现看涨期权的Delta对冲的最优化变成了之后研究的主要问题。为了克服一次性测度的随机性,本文采用随机100次模拟的方法,计算出工商银行看涨期权的对冲总成本的分布,对冲操作的间隔时长从每日4次下降到每20日一次(即在原有操作市场80倍的区间内)进行对冲,从而在不同交易成本计价方式下找到最优的对冲间隔时长。
通过模拟计算得到图2,可以看出在绝对交易成本0.02元每笔的条件下,总交易成本从每日4次对冲的近1.3元每笔经过对冲间隔时长的延伸不断波动下降,并在平均相隔19.25天(77次每日4次调整的间隔)的时长下达到20日内对冲成本的最小值0.6589元每笔,然而此时所对应的方差值也不断上升到了13.74%,为了在对冲总成本最小值和最小方差条件下进行平衡,本文在此衡量成本波动在不同的调频下的变化状况,并使用总成本+标准差的新条件对最优的成本值进行衡量。图2中标准差的最小值为9.84%位于5.5日时间间隔的对冲操作下,与单纯的最小总成本处相差55次(13.89天)对冲操作,计算得出77次相隔对冲处的成本方差之和为0.79626,而22次处的数值为0.83779。显然将最优的对冲频次定为了77次。
同样地,在相对交易成本为1%的条件下,进行同样的模拟。图3中,总成本期望值在从每天4次的对冲操作频次下的0.95每笔下降到每20天1次的对冲频次下的近0.6每笔的水平,其中在77次对冲时间间隔下期望成本达到了最小值(0.5804元每笔),同样在考虑了成本波动率的条件下,得到了成本的波动最小值为7.35%,其经过了平均10次(2.5天)的对冲时间间隔。通过计算发现,在成本最小时的成本波动率之和为0.7129元每笔,而在波动最小时的成本波动率之和为0.7315元每笔,故我们认为在1%相对交易成本的条件下经过77次1/4天的对冲操作间隔后进行对冲操作才能够使中国工商银行A股股权虚拟看涨期权的最优对冲得以实现。
五、总结
本文通过对工商银行2014年12月8日至2017年12月8日的收盘价数据和期间每年的股息率数据进行整理计算出了工商银行股价在未来6个月内的股价模拟数据、Delta值和动态看涨期权价格,之后在无交易成本条件下对半日、一日、两日、一周、两周、四周不同频次的对冲策略成本即标准差进行了计算,发现2日一次的对冲操作能够使得对冲成本优化。之后,为了使讨论的内容更加符合实际,本文将绝对交易成本和相对交易成本分别加入,并在每日4次的交易频次下算得二者的最优对冲策略为每77次即平均19.25天对冲一次。本文虽然是建立在工商银行虚拟期权条件下的最优对冲的设定,但是本文的价值在于通过模拟的方式再拓宽现有国内研究标的的条件下对股票期权交易过程的最优对冲策略构造进行了实证,可以为将来我国股票期权的交易对冲中的风险管理提供借鉴思路。
参考文献:
[1]熊熊,刘勇.上证50ETF期权动态Delta对冲策略及其实证检验[J].重庆理工大学学报(自然科学),2017(09).
[2]马子舜.结构化产品构建模式研究——基于Delta动态对冲策略的实证分析[J].武汉金融,2015(10).
[3]海通期货,完颜志翰.Delta风险的对冲[N].期货日报,2014-08-18.
(作者单位:贵州大学经济学院)

