迷宫流道滴头内流场和颗粒运动的不同湍流模型数值模拟

唐学林，赵旭红，李云开，李小芹,2

（1. 中国农业大学水利与土木工程学院，北京 100083；2. 北京市供水管网系统安全与节能工程技术研究中心，北京 100083）

0 引 言

滴灌是目前微灌系统中最有效、最先进的一种节水灌溉方式[1]，滴头内部流道结构错综复杂，消能效果非常好，但也存在滴头堵塞严重、灌水均匀度不高等问题。目前针对滴头内迷宫流道堵塞这一问题，国内外学者进行了大量的试验及模拟[2-5]，同时也对迷宫流道的结构作出了优化改进，但堵塞问题依然存在[4]，加上灌区水源多为井水、河水等近地表水，水质较差，使得灌水器堵塞已成为制约滴灌技术应用和推广的瓶颈[6]。优化滴头的抗堵塞性能，必须对其流道内部固-液两相的运动机理有一个较为全面的了解，进而分析滴头流道内部的流动，实现流道内部流体、颗粒流动的可视化[7]。

由于迷宫流道断面尺寸微小，一般在0.5～1.2 mm之间，介于微尺度（<1 mm）和常规尺度（>1 mm）之间[8-9]，加上结构复杂，使得迷宫流道滴头极易堵塞，为了更好地研究灌水器内部的临界尺度流动问题，在基于宏观尺度研究方法的CFD湍流模型流动分析的基础上，有待于依靠试验测试进行验证[10]。魏正英等[11-13]用激光多普勒测速仪(LDV)测量了流道中的速度流场，验证了流态模拟计算的正确性，之后又利用微 PIV对流道内两相流流场进行试验，指出造成流道堵塞的主要原因是流道内的漩涡区和低速区。喻黎明等[14-16]利用 PIV观测迷宫流道的抗堵塞性能进行验证数值模拟结果的准确性，并提出有效的抗堵塞优化设计方法，但对于致堵颗粒的运动研究多通过数理统计方法分析不同性质颗粒对于流道堵塞的影响。大量专家学者利用不同湍流模型开展迷宫流道内流场水力性能的分析，常用的湍流模型有标准k-ε模型、RNGk-ε模型和Realizablek-ε模型，并用PIV、micro-PIV等可视化测定结果进行验证，提出抗堵优化改进模型，魏正英等[12-15,17-23]利用离散相模型模拟离散相致堵颗粒在流道内水沙速度分布、流线分布及沙粒的运动轨迹和浓度的瞬时分布等，但未对不同颗粒的运动特性进行分析研究。

已发表的文献[15]基于非结构化网格和标准k-e湍流模型开展了迷宫流道内流动和颗粒运动研究，并未对离散相颗粒的运动规律作深入研究；为了深入分析不同性质致堵颗粒在流场内的运动规律，改善迷宫流道滴头的水力性能，本研究在文献[15]的基础上，采用高质量的结构化网格，进行了系列k-e湍流模型的适用性分析，并进一步深入分析了颗粒地运动规律。与已发表的文献[15]相比，本文更全面考虑颗粒的各种受力，预测不同密度和不同颗粒粒径下的颗粒运动轨迹变化规律，分析不同颗粒粒径下颗粒与其周围流体间的滑移速度变化规律，以及颗粒受到的曳力变化规律等，进一步为灌水器抗堵塞的优化设计提供可靠经验。

1 物理模型及网格划分

本文以齿形迷宫流道滴头为研究对象，进、出口平直流道各延长5 mm，以便于流体的充分发展，取8个流道单元以便于与文献[15]中的试验数据进行对照，滴头结构及参数示意图如图1所示。

图1 滴头结构及参数示意图（单位：mm）Fig.1 Structure and parameter of emitter (unit: mm)

应用UG软件构建物理模型，利用ICEM软件进行网格划分，基于分段划分的思想，将滴头分为进口段、迷宫流道段和出口段进行结构网格划分，考虑到流道单元拐角处为三角形块，选用Y-Block对其进行网格划分，流道的网格划分及网格无关性验证计算如图 2所示。为了更准确地模拟近壁区的流动状况，在流道近壁区网格进行加密，并通过网格无关性验证计算，最终选定网格数量约为27万个进行数值计算。

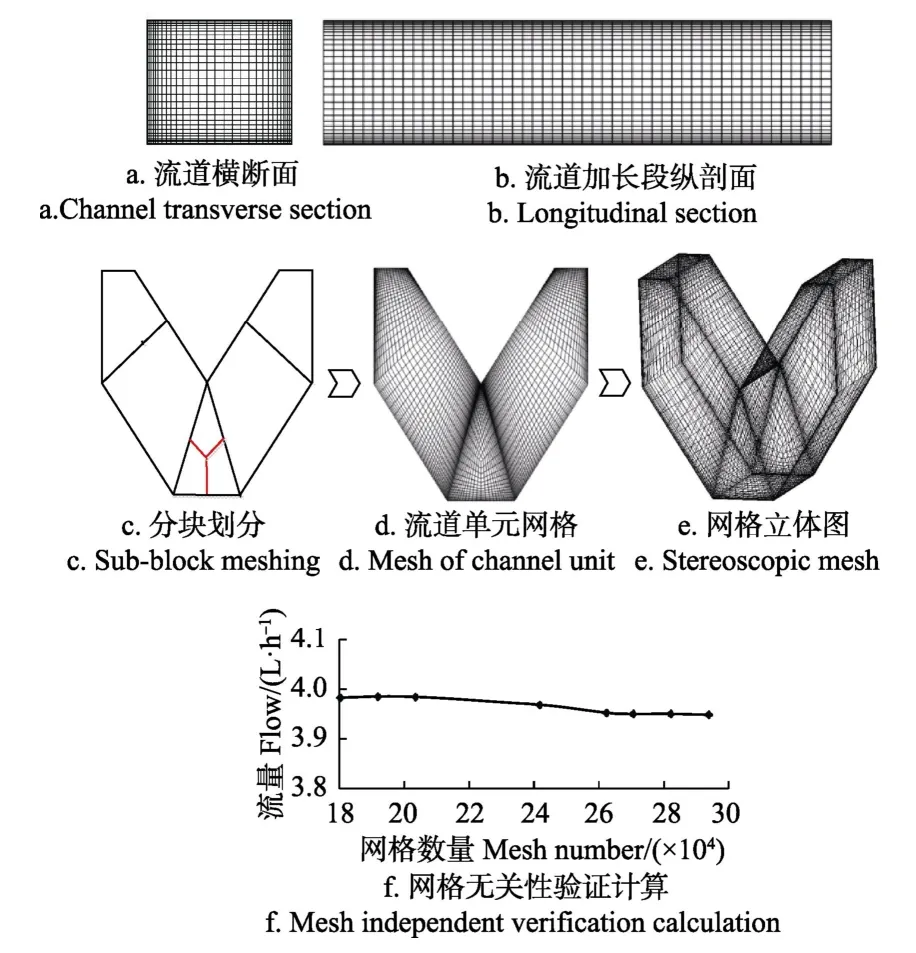
图2 滴头模型的网格划分与无关性验证计算Fig.2 Grid meshing and independent verification calculating of emitter model

2 数值计算与方法分析

为了选择适宜模拟本文滴头的湍流模型，开展系列k-e湍流模型的适用性分析，分别采用标准k-ε模型、RNGk-ε模型、Realizablek-ε模型进行滴头内连续相数值模拟。液相可视为典型的黏性不可压缩（ρ为常数）流体，并考虑重力作用。

连续相初步收敛后，创建离散相进行固-液相耦合计算。本文采用离散相模型进行稀两相流数值模拟，在离散相模型中一般要求颗粒相的体积分数小于 10%～12%[24-25]，文中使用单个颗粒，满足DPM模型使用的要求。

2.1 湍流模型

灌水器流动问题的数值模拟常用的湍流模型有标准k-ε、RNGk-ε和Realizablek-ε模型。为了比较不同湍流模型对迷宫流道滴头内流动模拟结果的影响，分别采用上述3种k-ε模型进行模拟。

标准k-ε模型是典型的两方程模型，由湍动能k输运方程和湍动耗散率ε方程组成。湍动能k是一个关于湍动粘度μt的函数；而RNGk-ε模型与Realizablek-ε模型在标准k-ε模型的基础上作了进一步改进，通过修正湍动粘度μt将小尺度运动从控制方程中去除，并在湍动耗散率ε方程中添加了反映主流的时均应变率，有效的提高了计算精度，但对于近壁区及低雷诺数流动区域，其模拟存在较大误差；Realizablek-ε模型进一步在湍动粘度μt的方程上进行改进，引入了有关旋转和曲率的内容，同时湍动耗散率ε方程中的产生项不再包含k方程中的产生项，有效应用于各种考虑旋转和大曲率的流动模拟[25-27]。

2.2 离散相模型

离散相模型（discrete phase model，DPM）是两相流的一种基本模型，其实质是基于欧拉-拉格朗日方法的稀两相流模型。在求解带有颗粒的流动中，把流体作为连续相，在欧拉坐标系下处理流场问题，而在拉格朗日坐标系下将颗粒作为离散存在的一个个颗粒。由于实际颗粒运动的随机性，连续相流场计算初步完成后，需要考虑湍流脉动对颗粒运动的影响，因此本文使用DPM中的随机轨道模型（stochastic trajectory model）来模拟颗粒物在流场内的运动问题。

对于颗粒在运动过程中受到的作用力，除了考虑颗粒本身的重力外，在颗粒运动过程中颗粒周围流体在外力的作用下会随着颗粒作相同方向的运动，相当于颗粒的一部分，称为虚拟质量力，这部分力对于粒径不同的颗粒运动有较大的影响。本文综合考虑重力、浮力、虚拟质量力和曳力的影响，将颗粒的重力和浮力合并表示为FM，对于压力梯度力、Saffman升力、热泳力、Basset力等，在本文中忽略不计。力的平衡方程[28-31]如式（1）所示。

式中mp为颗粒质量，kg；u为流体速度，m/s；up为颗粒速度，m/s；Fp为颗粒受到的惯性力，N；FM为考虑了浮力的颗粒相对重力，N；Fd为颗粒受到的曳力，N；Fm为颗粒受到的虚拟质量力，N；Cv为虚拟质量力系数；VP为颗粒体积，m3；dp为颗粒直径，m；ρp为颗粒密度，kg/m3；g为重力加速度，m/s2；ρ为流体密度，kg/m3；μ为流体动力粘度，Pa·s，取 10–3Pa·s；Rep为颗粒雷诺数（相对雷诺数）；CD为曳力系数，其中系数a1、a2和a3均为常数，按照式（7）计算，式中的系数采用经验系数[4]，具体取值如表1所示，对于Rep超过1 000的曳力系数，CD近似取为0.44。

表1 曳力系数a1、a2、a3的取值Table 1 constants for drag coefficient a1, a2, a3

2.3 计算方法及模拟参数设置

数值计算采用有限体积法离散控制方程，压力项等参数采用二阶迎风格式，速度和压力的耦合采用SIMPLE算法求解，流道壁面的处理采用标准壁面函数法，湍流对颗粒的随机影响采用随机轨道模型，收敛精度设为10-4。

为准确模拟流道内的颗粒运动，进一步与文献[15]试验数据进行对比，模拟中所用的颗粒密度、大小与文献[15]相同。试验采用密度分别为1 740 kg/m3的镁粉粒子、2 500 kg/m3的河砂粒子和2 870 kg/m3的铝粉粒子以及经过筛网挑选出的直径在58～65、90～100和125～150μm范围内的河砂粒子，经过充分搅拌形成浓度为12 g/L的稀两相流[18]，文献[15]采用颗粒的直径上限来开展研究；本文在模拟时，也采用颗粒直径上限，分别为 65、100和150μm，在进口断面中心位置水平投入单个颗粒。

3 结果与分析

3.1 湍流模型确定

试验用水为自来水，试验压力为0.01～0.08 MPa，每次测试时间为10 min，测试2次，取平均值计算各灌水器的流量[15]。本文设置进、出口为压力边界条件，进口压力水头分别为1、2、3、4、5、6、7、8 m，出口压力水头为0。

分别利用标准k-ε、RNGk-ε、Realizablek-ε模型对连续相流体进行数值模拟，得到相应的水力性能曲线，如图3所示。

图3 水力性能关系曲线Fig.3 Relationship curves of hydraulic performance

滴头的水力性能利用式（9）来表征，通过式（10）和式（11）计算得到不同模型下水力性能参数k与x，如表2所示。

式中q为出口流量，L/h；h为滴头的压力水头，m；k为滴头的流量系数；x为滴头的流态指数。

表2 不同计算模型的水力性能参数k、xTable 2 Hydraulic performance parameters k and x of different calculation models

根据表2中不同工况下的k、x、αk及αx发现，RNGk-ε与Realizablek-ε模型计算得到的k普遍比试验数据低，x普遍比试验数据高，标准k-ε模型的k与试验数据差距很小，相对误差仅为2.48%。同时，通过对图3中不同模型的水力性能曲线进行误差分析发现，RNGk-ε与Realizablek-ε模型模拟得到的水力性能曲线平均模拟误差分别为8.96%和8.11%，而标准k-ε模型模拟的平均模拟误差仅为2.32%。

综合比较发现，标准k-ε模型模拟预测的水力性能关系曲线与文献[15]试验数据更为接近，因此后续的离散相颗粒运动模拟基于标准k-ε模型内流场数值计算结果上进行，下文涉及到的数值模拟分析都是基于进口压力为4 m水头下进行的。本文的标准k-ε模型模拟误差略小于文献[15]的模拟误差 2.53%，这主要是由于文献[15]采用非结构化网格且网格数量较少，而本文采用高质量的结构化网格，为了保证后续离散相模拟过程的准确性，对计算模型进行高质量的网格划分，能进一步减少模拟误差，使模拟预测结果更为接近实际。

3.2 连续相分析

图4为流道纵向对称轴面的流场压力云图，观察图4发现，流道内的压力分布沿水流运动方向逐渐下降且变化均匀，压力变化基本发生在流道齿尖处，水流流经每个流道单元压力下降值基本相等。

图4 流道纵向对称轴面流场压力云图Fig.4 Pressure contour of longitudinal symmetry plane

图 5为流道不同截面的速度云图、等值线图和流线图。观察图5a发现，速度在每个流道单元内的分布规律相同；观察图5b中第5流道单元的速度云图和流线图发现，流道内流场按照流速大小可以分为 3部分，分别为低速区A、主流区B和高速发展区C，低速区A位于背水面齿尖拐角处，流线呈漩涡状，也称漩涡区[12]，主流区B流线平滑密集流速较高；图5c为1-1横截面速度等值线图，速度等值线关于y轴对称分布，从流道边壁到齿尖位置速度等值线图越来越密集，说明越靠近齿尖速度变化越剧烈，能量耗散越多。

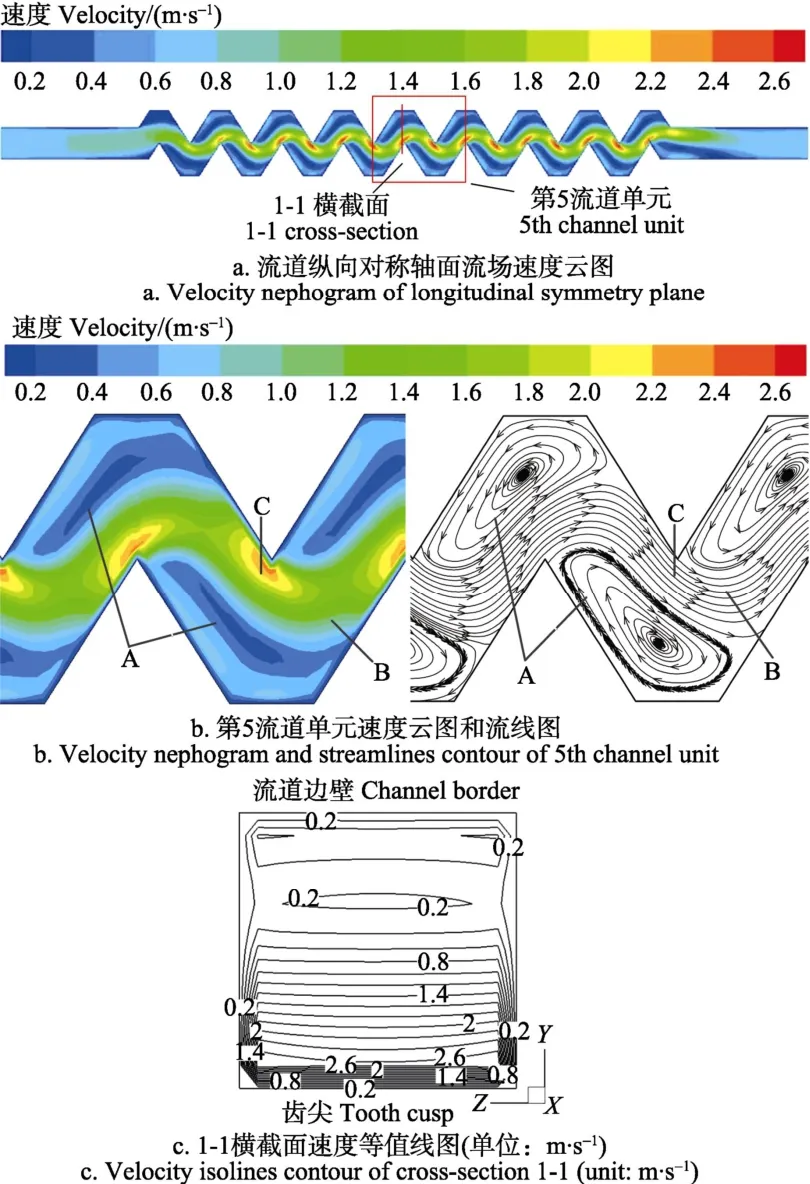
图5 流道不同截面的速度云图、等值线图Fig.5 Velocity nephogram and velocity isolines contour of different sections in flow channel

综合图5b和5c发现，高速发展区C靠近齿尖位置，流速在0.2～2.6 m/s范围变化，低速区A位于流道边壁附近，流速在0.2～0.8 m/s范围内变化，主流区B流速在0.8～2.0 m/s范围内变化。从而得出，流场内能量消耗主要发生在來流侧齿尖处，流体的动能转化为其他形式的能量耗散掉，从而达到消能效果。因此，为了提高滴头的消能能力，通过研究齿尖处拐角大小和结构形式与其他结构参数之间的关系来进一步设计出消能效果最好的流道结构。

3.3 离散相分析

3.3.1 不同密度颗粒的运动分析

分别模拟直径同为100μm，密度为1 740 kg/m3的镁粉、2 500 kg/m3的河砂和2 870 kg/m3的铝粉单个粒子在流场内的运动，结果如图6所示。

对比图6a、6d和6g中的流场速度云图可以看出，随着颗粒密度的增大，转角附近的高速发展区逐渐消失，主流区与低速区开始互相掺混，流场对颗粒的扰动作用增大。

对比图6b、6e和6h中颗粒模拟运动轨迹发现，颗粒直径相同的情况下，随着颗粒密度的增大，运动轨迹在旋涡区内路程增多。镁粉、河砂和铝粉粒子通过齿形迷宫流道滴头经过的路程分别为43.97，44.25和50.79 mm，由此可知，随着颗粒密度的增大，颗粒通过流道的路程增多，颗粒运动跟随性变差。图6b、6e和6h中粒子流经1-1横截面时，所对应的速度分别为1.09、1.05和1.00 m/s，由此可知，颗粒运动跟随性变差会导致颗粒速度减小。

对比图6b、6e和6h中CFD模拟轨迹与图6c、6f和6i中文献[15]PIV试验观测到的运动轨迹发现，CFD模拟得到的颗粒运动轨迹与 PIV试验观测到的颗粒运动轨迹虽然有所不同，但是轨迹运动的变化规律相同，这是由于文献[15]PIV试验测量结果的颗粒直径和颗粒释放的准确位置无法确定，故与本研究的模拟结果存在较小差异。

3.3.2 不同直径颗粒的运动分析

分别模拟颗粒密度同为2 500 kg/m3，直径为65、100和150μm的单个河砂粒子在流道内的运动，得到结果如图7所示。

对比图7a、7b和7c中颗粒的运动轨迹发现，当颗粒直径为65μm时，颗粒随主流区的水流运动，运动轨迹光滑有规律；当直径为100μm时，颗粒与流道边壁发生多次碰撞，颗粒的运动轨迹开始不再光滑，但运动轨迹仍然沿着主流区；当直径为150μm时，颗粒脱离主流区不断进入漩涡区，出现小漩涡现象，运动轨迹没有规律。3种直径颗粒通过流道的路程分别为 34.04，44.25和49.06 mm，由此可知，随着颗粒直径的增大，颗粒在漩涡区运动的路程增多，颗粒运动跟随性变差，颗粒直径变化较密度变化对颗粒运动影响大。

对比图7d、7e和7f中砂粒与周围流体的速度变化发现，当直径为65μm时，颗粒与流体的速度差异不大，颗粒与水流运动保持良好的一致性，速度整体变化幅值为3.60 m/s，速度均值为1.42 m/s；当直径为100μm时，颗粒与流体的速度差异增大，颗粒运动与流体基本保持一致，速度整体变化幅值为 2.19 m/s，速度均值为1.14 m/s；当直径为150μm时，颗粒速度与流体速度偏离更为明显，并出现了固液速度错峰的现象，速度变化越来越没有规律，速度整体变化幅值为1.93 m/s，速度均值为1.10 m/s。由此得出，随着颗粒直径的增大，颗粒与周围流体之间的速度偏差不断增大，速度整体变化幅值与均值减小。这是因为随着颗粒直径增大，颗粒运动过程中受到的阻力增大，使得颗粒运动跟随性变差，速度减小。

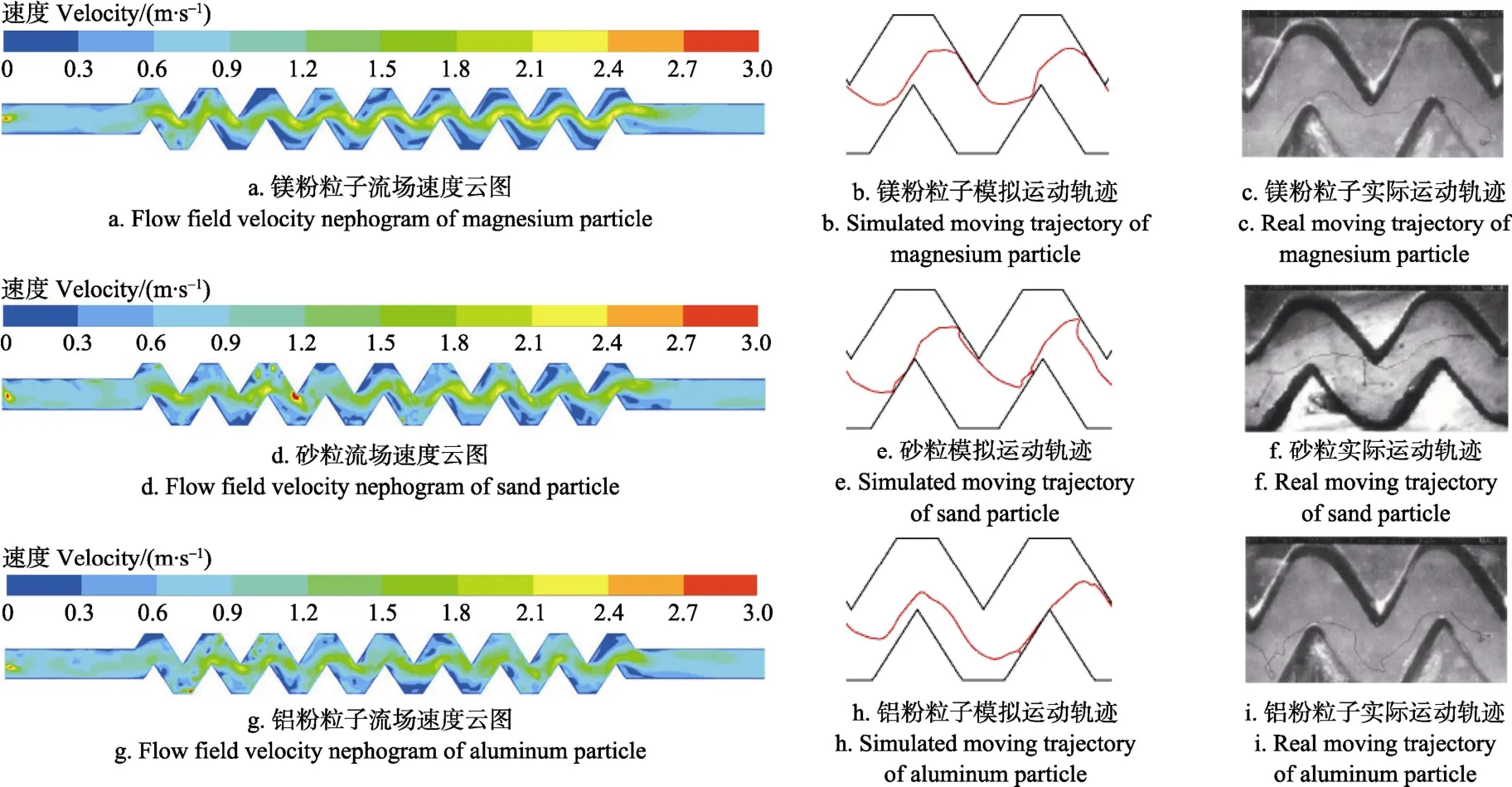
图6 不同密度颗粒所在流场的速度云图及其运动轨迹Fig.6 Flow field velocity nephogram and moving trajectory of single particle with different densities

图7 不同直径砂粒的运动轨迹、与周围流体的速度变化对比图Fig.7 Moving trajectory and velocity change with surrounding fluid of single sand particle with different diameters

图 8为不同直径砂粒所受曳力对比图，颗粒受到的曳力越来越大，变化幅度明显，结合图7a、7b和7c中颗粒的运动轨迹发现，随着颗粒直径增大，颗粒受到的曳力增大，颗粒运动随流性变差。

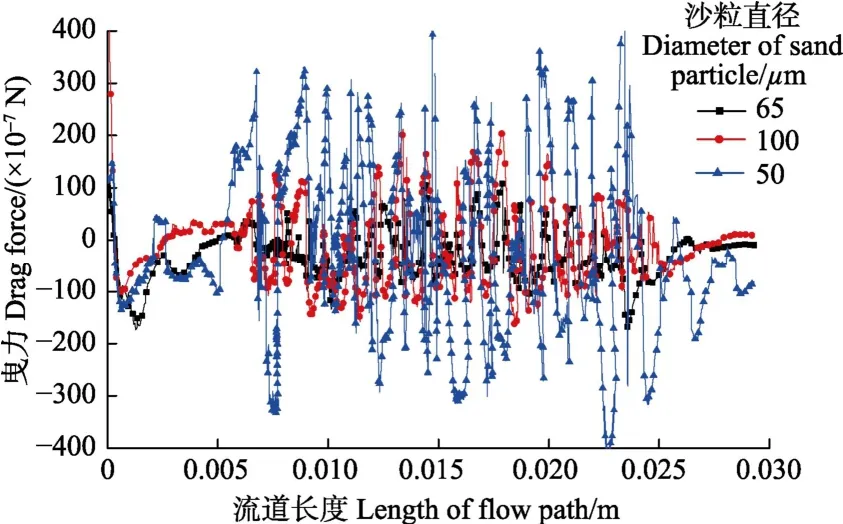
图8 不同直径单个砂粒所受曳力对比Fig.8 Drag force contrast of single sand particle with different diameters

3.3.3 颗粒运动速度变化分析

图9和图10分别为在不同密度和不同直径下，本文与文献[15]对相同的灌水器模型进行 CFD模拟和相应试验结果的比较，横坐标代表颗粒在流道长度方向的位置。图9中，随着颗粒密度增大，在13.0～16.9 mm这段流道长度内颗粒达到极值的次数分别为8、7和6次；图10中，随着颗粒直径增大，在13.0～17.4 mm这段流道长度内颗粒达到极值的次数分别为9、7和6次。相同长度的流道单元内速度极值出现的次数减少，颗粒速度变化变剧烈，这是由于随着密度或直径的增大，颗粒受到阻力的影响增大，在惯性的作用下易被甩离高速发展区，速度减小，颗粒逐渐往速度减小的区域运动。

图11为不同工况下的颗粒速度幅值变化图，为了保证结果的准确度，对图11中每个工况下的速度都取平均值。图11a和11b分别为颗粒运动速度极大值随着颗粒密度和直径增大的变化图，速度极大值随着密度或直径的增大变化不大，均在2.1～2.5 m/s内变化，本文运动速度极大值的模拟误差为 1.5%，而文献[15]的模拟误差为6.0%；图11c和11d分别为颗粒运动平均速度随着颗粒密度和直径增大的变化图，平均速度随着密度或直径的增大逐渐减小，在1.1～1.8 m/s内变化，减小幅度基本相同，本文运动平均速度的模拟误差为 2.7%，而文献[15]的模拟误差为7.1%；图11e和11f分别为颗粒运动速度极小值随着颗粒密度和直径增大的变化图，随着颗粒直径和密度增大，速度幅值减小程度从大到小依次为：颗粒直径、颗粒密度，本文运动速度极小值的模拟误差为3.0%，而文献[15]的模拟误差为 9.2%。由此说明，随着颗粒直径或密度增大，颗粒整体运动速度减小，颗粒运动速度极小值受其影响最大，颗粒运动平均速度受其影响次之，颗粒运动速度极大值受其影响最小。

图9 不同密度的颗粒运动速度对比Fig.9 Comparison of particle velocity with different densities

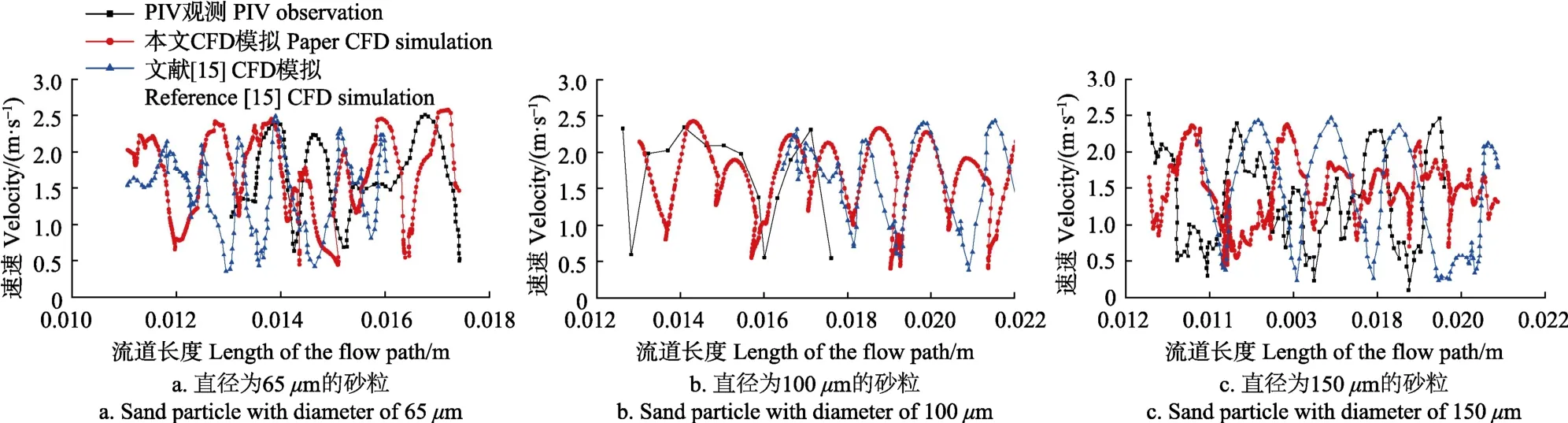
图10 不同直径的砂粒运动速度对比Fig.10 Comparison of sand particle velocity with different diameters

图11 不同工况下的颗粒运动速度幅值对比Fig.11 Comparison of particle movement velocity amplitude in different conditions

图 11中本文对颗粒运动速度的平均模拟误差为2.34%，比文献[15]平均模拟误差减少了 5.05%，结果更加接近 PIV试验数据，这是由于本文针对颗粒受力不仅考虑了重力与曳力，还考虑了颗粒的浮力与虚拟质量力对于离散颗粒运动的影响，比文献[15]只考虑重力与曳力的模拟结果更符合颗粒运动客观规律。

4 结 论

1）通过k-ε系列模型的数值模拟结果与PIV试验数据的对比，分析了各湍流模型在迷宫流道滴头内流动的适应性，结果表明，标准k-ε模型预测结果最接近PIV试验数据，水力性能曲线平均模拟误差仅为2.32%。

2）随着颗粒密度增大，液相流场受颗粒扰动变大且主流区与低速区开始互相掺混，颗粒运动跟随性变差；随着颗粒直径的增大，颗粒与周围流体之间的速度偏差不断增大，速度整体变化幅值与均值减小。颗粒受到的曳力增大，颗粒运动速度与液相速度出现峰值错乱现象，颗粒运动轨迹变乱，颗粒在惯性力的作用下更容易被带入漩涡区，颗粒的运动速度减小，最后可能沉积在流道拐角内侧的漩涡区，易造成迷宫流道堵塞。

3）随着颗粒直径或密度增大，颗粒整体运动速度减小，颗粒运动速度极小值受影响最大，颗粒平均运动速度受影响次之，颗粒运动速度极大值受影响最小，从而证明，级配颗粒运动速度随其直径和密度不同而变化很大。

4）通过随机轨道模型模拟颗粒运动，基于文献[15]的数值研究，进一步综合考虑了虚拟质量力、重力、曳力和浮力对于颗粒运动的影响，模拟结果更加接近 PIV试验数据，颗粒运动速度的平均模拟误差仅为2.34%，颗粒运动轨迹更符合客观规律。

[1]张俊，赵万华，粟晓玲，等. 微灌长流道灌水器结构特性的研究综述[J]. 农业工程学报，2005，21(1)：182－185.Zhang Jun, Zhao Wanhua, Su Xiaoling, et al. Review of structural characteristics analysis of the long-path emitters formicroirrigation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2005,21(1): 182－185. (in Chinese with English abstract)

[2]Sahin U, Anapali O, Dönmez M F, et al. Biological treatment of clogged emitters in a drip irrigation system[J]. Journal of Environmental Management, 2005, 76(4): 338－341.

[3]Wei Q, Gang L, Jie L, et al. Evaluations of emitter clogging in drip irrigation by two-phase flow simulations and laboratory experiments[J]. Computers & Electronics in Agriculture, 2008, 63(2): 294－303.

[4]Zhang Jun, Zhao Wanhua, Tang Yiping, et al. Anti-clogging performance evaluation and parameterized design of emitters with labyrinth channels[J]. Computers and Electronics in Agriculture, 2010, 74(1): 59－65.

[5]冯吉，孙昊苏，李云开. 滴灌灌水器内颗粒物运动特性的数字粒子图像测速[J]. 农业工程学报，2013，29(13)：90－97.Feng Ji, Sun Haosu, Li Yunkai. Visualizing particles movement characteristics in drip irrigation emitters with digital particle image velocimetry[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(13): 90－97. (in Chinese with English abstract).

[6]李云开，冯吉，宋鹏，等. 低碳环保型滴灌技术体系构建与研究现状分析[J]. 农业机械学报，2016，47(6)：83－92.Li Yunkai, Feng Ji, Song Peng, et al. Developing situation and system construction of low-carbon environment friendly drip irrigation technology[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(6): 83－92. (in Chinese with English abstract)

[7]李云开，冯吉. 滴灌灌水器内部水动力学特性测试研究进展[J]. 排灌机械工程学报，2014，32(1)：86－92.Li Yunkai, Feng Ji. Progress in measurement of hydrodynamic characteristics in drip irrigation emitters[J].Journal of Drainage and Irrigation Machinery Engineering,2014, 32(1): 86－92. (in Chinese with English abstract)

[8]李云开，杨培岭，任树梅，等. 圆柱型灌水器迷宫式流道内部流体流动分析与数值模拟[J]. 水动力学研究与进展(A 辑)，2005，20(6)：736－743.Li Yunkai, Yang Peiling, Ren Shunmei, et al. Analyzing and modeling flow regime in labyrinth path drip irrigation column emitter with CFD[J]. Journal of Hydrodynamics: Ser A, 2005, 20(6): 736－743. (in Chinese with English abstract)

[9]李云开，杨培岭，任树梅，等. 圆柱型迷宫式流道滴灌灌水器平面模型试验研究[J]. 农业机械学报，2006，37(4)：48－51.Li Yunkai, Yang Peiling, Ren Shunmei, et al. Plane model of labyrinth path drip irrigation column emitter[J]. Transactions of the Chinese Society for Agricultural Machinery, 2006,37(4): 48－51. (in Chinese with English abstract)

[10]Liu H, Huang G. Laboratory experiment on drip emitter clogging with fresh water and treated sewage effluent. Agric Water Manag[J]. Agricultural Water Management, 2009,96(5): 745－756.

[11]魏正英，赵万华，唐一平，等. 滴灌灌水器迷宫流道主航道抗堵设计方法研究[J]. 农业工程学报，2005，21(6)：1－7.Wei Zhengying, Zhao Wanhua, Tang Yiping, et al.Anti-clogging design method for the labyrinth channels of drip irrigation emitters[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2005, 21(6): 1－7. (in Chinese with English abstract)

[12]魏正英，唐一平，温聚英，等. 灌水器微细流道水沙两相流分析和微PIV及抗堵实验研究[J]. 农业工程学报，2008，24(6)：1－9.Wei Zhengying, Tang Yiping, Wen Juying, et al. Two-phase flow analysis and experimental investigation of micro-PIV and anti-clogging for micro-channels of emitter[J].Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2008, 24(6): 1－9.(in Chinese with English abstract)

[13]Wei Zhengying, Cao Meng, Liu Xia, et al. Flow behaviour analysis and experimental investigation for emitter micro-channels[J]. Chinese Journal of Mechanical Engineering, 2012, 25(4): 729－737.

[14]喻黎明，梅其勇. 迷宫流道灌水器抗堵塞设计与PIV试验[J]. 农业机械学报，2014，45(9)：155－160.Yu Liming, Mei Qiyong. Anti-clogging design and experimental investigation of PIV for labyrinth-channel emitters of drip irrigation emitters[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(9): 155－160. (in Chinese with English abstract)

[15]喻黎明，吴普特，牛文全，等. 迷宫流道内固体颗粒运动的CFD模拟及PIV验证[J]. 农业机械学报，2009，40(5)：45－51.Yu Liming, Wu Pute, Niu Wenquan, et al. CFD numerieal simulation and PIV verification about the movement of solid particles in labyrinth channel[J]. Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(5): 45－51. (in Chinese with English abstract)

[16]牛文全，喻黎明，吴普特，等. 迷宫流道转角对灌水器抗堵塞性能的影响[J]. 农业机械学报，2009，40(9)：51－55.Niu Wenquan, Yu Liming, Wu Pute, et al. Influence of angle of labyrinth channels on anti-clogging performance of emitter[J]. Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(9): 51－55. (in Chinese with English abstract)

[17]张俊, 魏公际, 赵万华. 灌水器内圆弧形流道的液固两相流场分析[J]. 中国机械工程, 2007, 18(5)：589－593.Zhang Jun, Wei Gongji, Zhao Wanhua. Numerical analysis on liquid-solid two-phase flows in arc-type channel of the emitter[J]. China Mechanical Engineering, 2007, 18(5): 589－593. (in Chinese with English abstract)

[18]喻黎明. 滴灌灌水器水力特性及抗堵塞研究[D]. 杨凌：西北农林科技大学，2009.Yu Liming. Study on Hydraulic and Anti-clogging Performance of Drip Emitter[D]. Yangling: Northwest A&F University, 2009. (in Chinese with English abstract)

[19]常莹华，牛文全，王维娟. 滴灌灌水器迷宫流道的内部流体数值模拟与流动分析[J]. 西北农林科技大学学报(自然科学版)，2009，37(2)：203－208.Chang Yinghua, Niu Wenquan, Wang Weijuan. Numerical simulation and flow analysis of labyrinth path of drip irrigation emitters[J]. Journal of Northwest A&F University(Natural Science Edition), 2009, 37(2): 203－208. (in Chinese with English abstract)

[20]喻黎明，谭弘，邹小艳，等. 基于CFD-DEM耦合的迷宫流道水沙运动数值模拟[J]. 农业机械学报，2016，47(8)：65－71.Yu Liming, Tan Hong, Zou Xiaoyan, et al. Numerical simulation of water and sediment flow in labyrinth channel based on coupled CFD-DEM[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(8): 65－71. (in Chinese with English abstract)

[21]邓涛，魏正英，王立朋，等. 压力补偿灌水器分步式CFD设计与实验研究[J]. 清华大学学报(自然科学版)，2012，52(4)：513－516.Deng tao, Wei Zhengying, Wang lipeng, et al. Stepwise CFD simulation and experiments of pressure-compensating emitters[J]. Journal of Tsinghua University (Natural Science Edition), 2012, 52(4): 513－516. (in Chinese with English abstract)

[22]金文，张鸿雁，何文博. 灌水器流道结构对水力性能影响的数值分析[J]. 中国农业大学学报，2012，17(2)：139－143.Jin Wen, Zhang Hongyan, He Wenbo, et al. Numerical investigation on effect of channel structure to hydraulic performance of emitter[J]. Journal of China Agricultural University, 2012, 17(2): 139－143. (in Chinese with English abstract)

[23]张重，任树梅，杨培岭，等. 圆柱型灌水器迷宫式流道内部流体流动的CFD模拟精度研究[J]. 中国农业大学学报，2016，21(9)：149－155.Zhang Chong, Ren Shumei, Yang Peiling, et al. Research on the CFD simulation accuracy of labyrinth path drip irragation cylindrical emitter[J]. Journal of China Agricultural University, 2016, 21(9): 149－155. (in Chinese with English abstract)

[24]李亚林，袁寿其，汤跃，等. 离心泵内示踪粒子运动的离散相模型模拟[J]. 农业机械学报，2012，43(11)：113－118.Li Yalin, Yuan Shouqi, Tang Yue, et al. Simulation of tracer particles movement by discrete phase model in the centrifugal pump[J]. Transactions of the Chinese Society for Agricultural Machinery, 2012, 43(11): 113－118. (in Chinese with English abstract)

[25]唐学林，李林伟，苏砚文，等. 螺旋槽流道微泵的数值模拟方法分析[J]. 排灌机械工程学报，2010，28(1)：31－37.Tang Xuelin, Li Linwei, Su Yanwen, et al. Analysis of numerical simulation method for flow inside micro-machined spiral-channel pump[J]. Journal of Drainage and Irrigation Machinery Engineering, 2010, 28(1): 31－37. (in Chinese with English abstract)

[26]金文. 微灌滴头微通道内流流场实验研究与数值模拟[D].西安：西安建筑科技大学，2010.Jin Wen. Experimental Research and Numerical Simulating Approaches on Internal Flow Fields of Micro Channel in Micro-irrigation Emitter[D]. Xi¢an: Xi'an University of Architecture and Technology, 2010. (in Chinese with English abstract)

[27]王福军. 计算流体动力学分析：CFD软件原理与应用[M].北京：清华大学出版社，2004.

[28]Zhang J, Zhao W, Tang Y, et al. Numerical investigation of the clogging mechanism in labyrinth channel of the emitter[J].International Journal for Numerical Methods in Engineering,2010, 70(13): 1598－1612.

[29]Fluent Inc. Fluent6. 3 User's Guide[M]. Lcbanon: Fluent Inc.,2006.

[30]Mei R, Adrian R J, Hanratty T J. Particle dispersion in isotropic turbulence under Stokes drag and Basset force with gravitational settling[J]. Journal of Fluid Mechanics, 1991,225: 481－495.

[31]陈彬，颜欢，刘阁，等. 流固两相流的稀疏离散相模型研究进展[J]. 化工进展，2016，35(11)：3400－3412.Chen Bin, Yan Huan, Liu Ge, et al. Progress in the dilute discrete model of fluid-solid two phase flow[J]. Chemical Industry and Engineering Progress, 2016, 35(11): 3400－3412.(in Chinese with English abstract)