基于单目视觉的平面靶标姿态测量及其仿真
苏建东,段修生,齐晓慧
(陆军工程大学石家庄校区,石家庄 050003)
0 引言
视觉测量是将计算机视觉应用于空间几何尺寸的精确测量和定位的方法[1]。视觉测量技术以其非接触性、测量精度高、响应速度快、不易受干扰等特点,正逐渐应用到航空航天[2-3]、军事装备[4]、目标识别[5]、装备制造[6]、工业测量和自动化控制等诸多领域。
视觉测量在空间物体的位置和姿态求解等空间定位问题中应用广泛,该类问题所用到的几何特征可以分为点、直线和高级几何特征等几类,其中基于点特征的视觉定位问题通常被称为PnP问题,其研究最为广泛和成熟[7]。张正友等人提出了一种基于平面靶标的摄像机标定方法[8],受该方法启发本文提出了一种基于单目视觉的平面靶标姿态测量方法,在获取摄像机内参以后,根据多点透视问题解的稳定性,结合最小二乘拟合算法得到相应位置的外参矩阵,并利用Givens矩阵对外参矩阵进行分解,从而求得靶标的3个姿态角。
仿真系统由于没有图像噪声、模型误差和机械震动等其他不确定因素,因此,可以用来验证相关算法的正确性与准确性,分析算法的精度,为进一步优化测量算法提供方向。目前摄像机成像仿真技术,大部分的研究是在摄像机线性模型的基础上,加上镜头的畸变、景深效应、光线和色彩等因素。研究点不同,侧重点也就不同,以闫龙[9]、张子淼[10]为代表的一批学者在摄影仿真方面取得了一些成果,但在具体的应用中缺乏针对性,结合具体的应用背景,本文设计了一套简单有效的仿真系统,并对文中提出的解算方法进行了验证。
1 摄像机成像模型及其标定
先给出棋盘状靶标在理想针孔成像模型下的成像过程示意图,如图1所示。

图1 棋盘状靶标成像示意图
图中定义了4个坐标参考系,其中ow-xwywzw是三维直角坐标系,简称世界坐标系。oc-xcyczc是相机三维直角坐标系,简称摄像机坐标系,其zc轴与相机镜头的光轴重合,摄像机坐标系可在世界坐标系的任意位置。op-xpyp是图像二维直角坐标系,简称图像坐标系,一般都以像素为单位定义图像上点的坐标,ob-xbybzb是以棋盘状靶标所在的平面为xy面的三维直角坐标系,简称靶标坐标系,其随靶标位置姿态变化而变化。
在不考虑镜头畸变的情况下,靶标上任一角点P在靶标坐标系下的齐次坐标向量Pb与其投影点p在图像坐标系下的齐次坐标向量Pp满足关系:
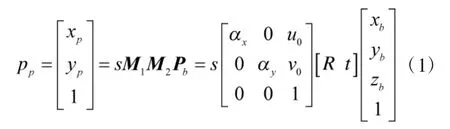
式中,zb=0;M1为相机内参矩阵;αx和 αy分别为相机镜头在x轴和y轴上的归一化焦距;u0和v0则是光轴与成像面角点在图像坐标系下的偏移,内参矩阵在相机安装好镜头、调焦完毕之后就不变了;M2为外参矩阵,不同的靶标坐标系对应一个不同的外参矩阵;R 为旋转矩阵,设 R=[r1,r2,r3],t为平移向量,设 t=[t1,t2,t3]。
获取多幅模板在不同姿态下的图像进行相机标定,即求解出相机内参。求解内参矩阵的算法是基于张正友提出的张氏定法。
对每一幅图像,标定模板平面上的点与其像点之间建立了一个Homography映射,定义单应性矩阵:


根据正交矩阵的性质,对于每一幅图像可以得到约束方程:
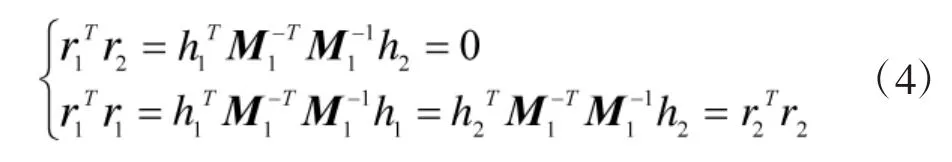
这是摄像机内参的两个基本约束,令:
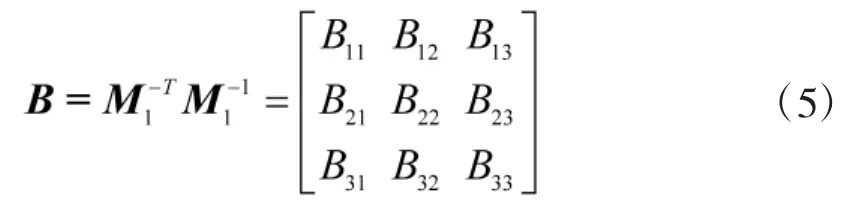
B是对称矩阵,可以另表示为下面的六维向量:
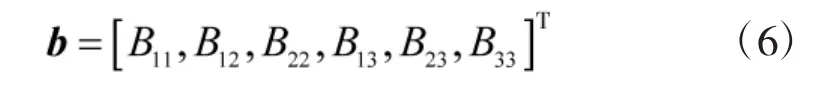

这样,约束方程就可以写成两个以b为未知数的齐次方程:
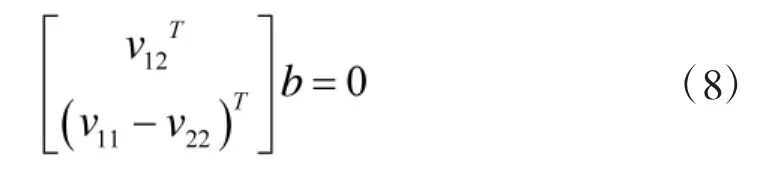
可见只需堆叠其中3幅图像的方程,可以解出b,那么摄像机内参数可以从B矩阵的封闭解中直接得到,计算如下:

2 靶标位姿解算
对每一幅图像,外参数可以由单应性条件计算得到,计算如下:

测量时首先采集零位置图像,作为测量基准,然后采集待测姿态图像。按照上述方法分别计算其旋转矩阵R0,Rn。则其由零位置至待测位置的旋转矩阵为:

对该矩阵选择合适的参数分解,即可求得3个姿态角 α1、α2、α3,求解过程如下:
定义3个三阶Givens旋转矩阵:

令

选择合适的参数使得L的l32元素变为0,即

3 仿真模型及其推导
仿真试验可运用仿真得到的图像代替摄像机实际采集的图像,进行摄像机标定、角点的提取和姿态角的解算,并将解算结果和仿真输入作对比,以判断测量算法的准确性。
3.1 空间点坐标计算
如图2所示,以角点数为8×8的棋盘格靶标为例,给棋盘格上所有的角点编号,建立右手直角坐标系,并设定该坐标系即为世界坐标系ow-xwywzw。

图2 角点标号及坐标系
设第i行j列的任意一角点P在世界坐标系的初始坐标为:
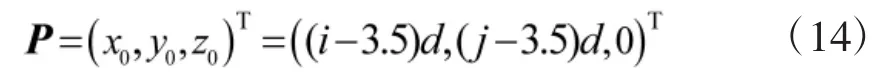
其中,d为棋盘格每个小方块的边长。
当靶标仅绕xw轴旋转α1时,角点P旋转后的坐标为:
同理,当靶标分别仅绕yw轴和zw轴旋转α2和α3时,角点P的坐标分别为:
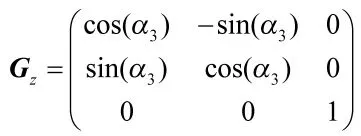
当棋盘格靶标由初始位置转到任意位置时,其旋转过程可分解为:先绕xw轴转α1,再绕yw轴转α2,最后绕zw轴转α3。则点P旋转之后的世界坐标为:

3.2 投影点图像坐标计算
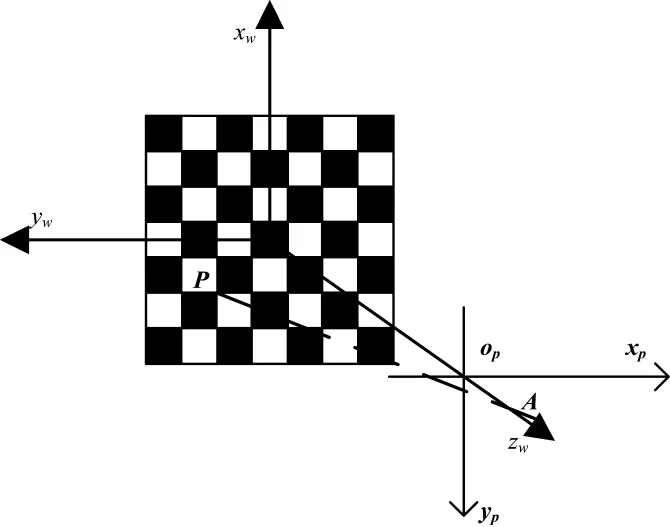
图3 角点投影示意图
设A点为摄像机所在的位置,其在世界坐标系下的坐标为PA。角点P旋转后在空间的坐标(x1,y1,z1)T可由式(18)求得,建立 AP 的空间直线方程,该直线与投影面的交点即为投影面内角点的坐标,这就是建立仿真模型时需要标绘的点。
如图3所示,为简化成像模型,假定点A在世界坐标系的 zw轴上,其坐标为 PA=(0,0,d1)T,d1是摄像机到坐标原点的距离。成像面垂直于zw轴,建立图像坐标系op-xpyp,使opxp轴平行于owyw轴,摄像机焦距为f,设投影点在世界坐标系内的坐标为Pw,在图像坐标系内的坐标为Pp,则

其中,R2×3是坐标系世界坐标系和图像坐标系间的坐标变换矩阵。
世界坐标系中直线AP的两点式方程为:
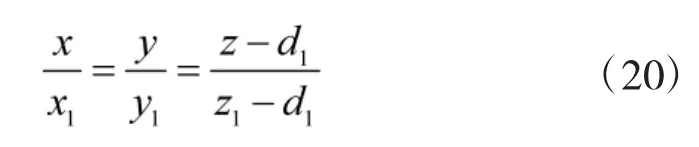
令z=d1-f,可得AP与投影面的交点世界坐标为:

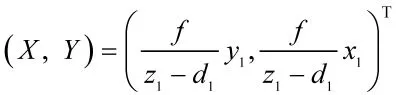
4 仿真试验及分析
使用上文设计的仿真试验系统,生成靶标在不同姿态下的仿真图像,设 α1、α2、α3分别为靶标绕 xw、yw、zw轴转过的角度。图4所示为靶标在几组不同姿态下的仿真图像。
仿真试验过程中用仿真图像代替摄像机实际采集图像进行角点提取、摄像机标定、角度解算等操作,并将解算得到的角度和仿真输入作对比,仿真试验结果如下页表1所示,由表1可知仿真试验平均精度可以达到0.05°,并且绕zw轴转角的精度明显高于其他两轴,分析认为这是由于仿真系统中zw轴为光轴方向,靶标绕zw轴转动是垂直于光轴的,靶标绕其他两轴转动均会产生沿光轴运动的分量。单摄像机对于景深信息不敏感,造成了上述试验结果,这与晁志超[11-12]等人的研究结果是一致的。

图4 几组不同姿态下的仿真图像
表1的试验结果虽然可以达到0.05°的精度,但是经分析不难发现,仿真图像提取角点时只能达到像素级,这相当于在图像上加了很强的高斯噪声,为了分析角点提取精度带来的误差,做了以下两组试验。
第1组试验将理论计算得到的投影角点坐标代替仿真提取坐标直接用于姿态解算,结果如表2所示。不难发现结果基本和仿真输入一致,最大误差不超过0.000 02°。有限的几组误差也是数值计算导致的。表2的结果可以说明本文提出的平面靶标姿态解算方法,理论上是可行的,并且在测量精度上有很大的潜力。

表1 仿真试验结果(单位:°)

表2 理论试验结果(单位:°)
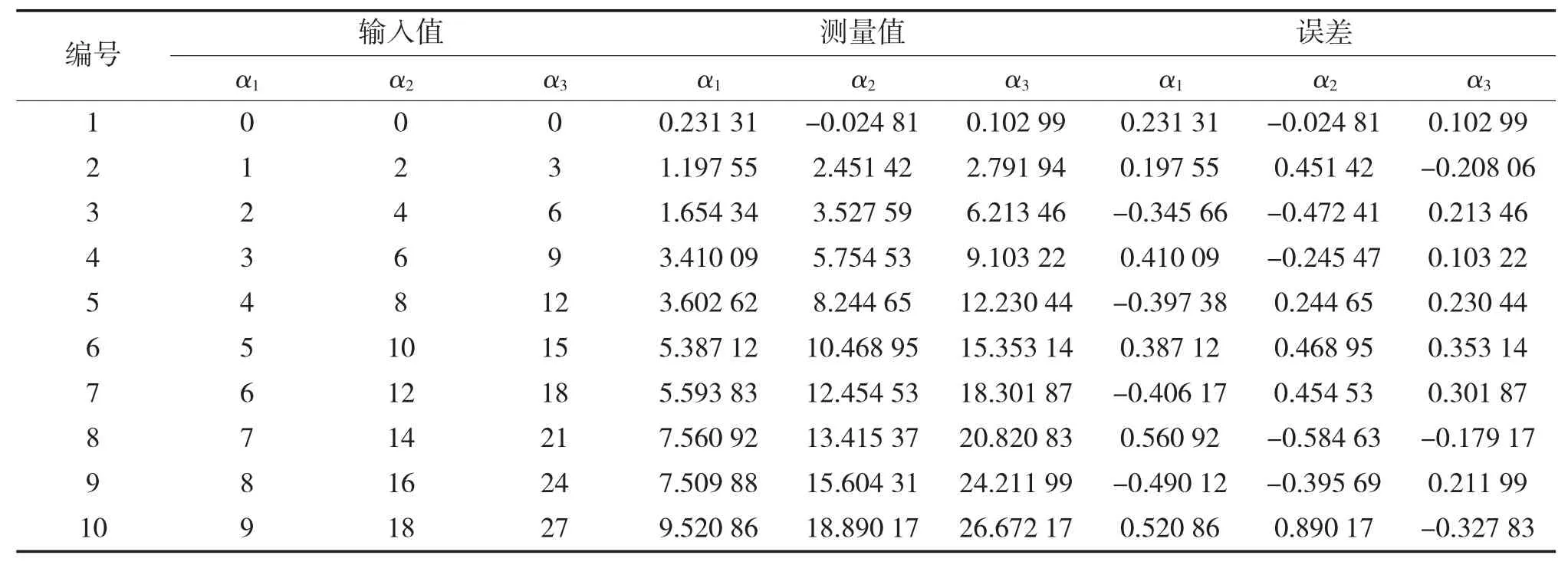
表3 降低分辨率后的仿真试验结果(单位:°)
第2组试验是修改仿真模型参数,降低仿真图像分辨率。姿态解算时仍使用仿真图像去提取角点坐标,结果如表3所示。不难发现降低分辨率以后测量精度明显变差,精度只有0.5°左右,误差最大值甚至接近1°,与表1结果相比差了一个数量级。分析认为这是由于降低分辨率后仿真图像仍然提取像素级坐标,与此相对的是表1试验中虽然也是像素级坐标,但是两者图像分辨率差了10倍。因此,相对于本组试验,表1结果也就相当于提取的“亚像素级”的角点坐标,所以表1测量结果精度更高。
综合表1~表3的试验结果可知:图像分辨率越高、角点检测精度越高,测量误差也就越小。可以分析如果对表1所用图像进行亚像素级提取其精度可以提高约一个数量级,预期精度可达0.005°~0.01°左右。
5 结论
本文提出了一种基于单目视觉的平面靶标姿态测量方法,并基于摄像机成像模型和靶标运动分析设计一套仿真试验系统。仿真试验结果表明本文所提姿态测量方法可行有效,其仿真测量精度可达0.05°,理论精度可达0.000 02°,实际应用精度期望达到0.005°~0.01°。分析全文仍存在以下不足:建立仿真模型时未考虑畸变参数,将其默认为0,这与实际明显不符,可进一步完善仿真模型,并且增加图像畸变矫正的过程,丰富整个仿真系统。

