一种提升图书推荐精度的协同过滤改进算法

柯秀文

(商丘职业技术学院 软件学院，商丘 476001)

0 引言

随着现代信息技术的高速发展，给社会各行各业带来了革命性的变革，提供高效、优质的服务是很多行业追求的目标。信息技术的广泛应用为各级各类图书馆提供了新的服务方向和选择。根据读者的需求，提供差异化、高质量的个体服务，是各级各类图书馆在新时期深化图书馆服务职能的积极尝试和有益探索，也是信息服务的必然需求。传统的图书搜索引擎只能为所有读者展现相同的图书排序结果，无法结合读者的个人爱好提供差异化的检索结果，而基于协同过滤算法的图书推荐系统却能够根据读者的个人偏好为其提供差异化的图书推荐[1]。

然而，随着各级各类图书馆开放程度和服务质量的提升，推荐系统中读者与图书数量的增加和积累，评分矩阵数据稀疏性问题越来越显著，此外，传统的基于内存的协同过滤算法没有考虑时间因素等上下文信息对相似度造成的影响，这些都导致图书推荐质量的下降。因此，本文提出一种改进的协同过滤算法，以提高图书推荐质量，实验证明，改进的协同过滤算法能够有效提高图书推荐精度。

1 协同过滤算法及改进思路

协同过滤( Collaborative Filtering，CF)是当前使用最为广泛的推荐算法之一，这个概念由 Goldberg等在1992年正式提出[2]，它依据用户-项目评分数据，算法基于用户对一些项目的评分进行比较，假设用户对一些项目评分相似，那么用户对其他项目评分也相似[3]。

随着读者与图书数量的增加和积累，评分矩阵数据稀疏性问题越来越显著，为了解决数据稀疏环境下读者对图书预测评分的准确度问题，提出一种改进的协同过滤方法 ICF(Improved Collaborative Filtering)，从2个方面改进推荐算法：首先，将LDA模型应用在图书馆图书推荐上，将读者和图书通过潜在主题关联，将得到的读者对图书的选择概率作为预处理数据，进而将相似度计算转至低维潜在因素空间，减少数据稀疏所带来的影响。其次，在相似度计算时，考虑时间因素对读者图书偏好的影响，引入Sigmoid函数，改进读者相似度计算公式，预测读者对未选择图书的评分。

2 协同过滤算法的改进

协同过滤算法的改进主要分为3个步骤：首先基于LDA(Latent Dirichlet Allocation)模型[4]建立读者-图书概率矩阵，并对图书进行聚类，裁剪概率矩阵。其次考虑时间因素对读者偏好动态变化的影响，引入时间因子sigmoid函数，作为评分时间影响权重，改进相似度计算方法，计算邻居读者。最后利用协同过滤算法预测读者对未选择图书的评分。

2.1 读者-图书选择概率矩阵

LDA模型通过主题将文档和单词联系起来，以实现对文本信息的挖掘，在新浪微博等相关网站上广泛应用。其核心思想是：

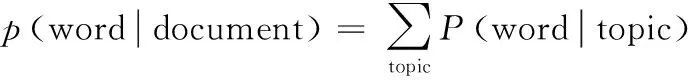
Ptopicdocument

本文根据读者评分信息建立读者图书伪文档，将读者对应文档，图书对应单词，每个读者喜欢的图书种类有很多，每个图书种类由若干图书构成，读者的评分数值对应该图书在该读者图书文档中出现的次数。基于此建立的读者-图书LDA模型，如图1所示。

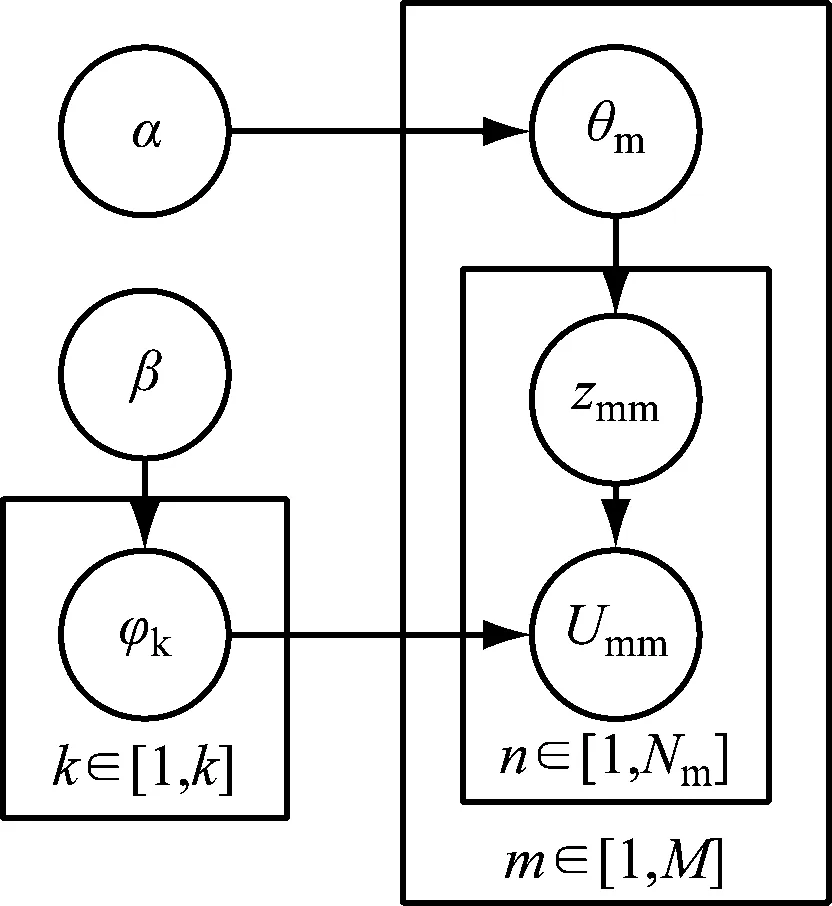
图1 读者-图书的LDA模型

在图1各种关系中，θ是读者的图书主题分布，φ是图书主题的图书分布，且都满足Dirichlet分布，α、β分别是θ和φ的超参数，K、N、M分别是图书主题数、图书数和读者数，Zmn表示读者m选择的图书n对应的主题，Umn表示读者m选择的图书n。

假设系统中有n个读者以及m个图书，并且读者i对图书j的评价通过整数1-5的评分表示，记做Rij。某读者j对图书的评分信息，如表1所示。

在预处理阶段，将表1的相关信息处理为：读者Uj=﹛i1，i2，i2，i2，i3，i3，i3，i3，i3，i5，i5﹜。以此类推，可以得到每个读者的伪文档。

以此为基础，本文采用Gibbs Sampling采样算法训练读者图书LDA主题模型。根据对相关文献的研究，LDA模型参数通常取值为α=50/K，β=0.01，K为主题的个数。对读者图书LDA主题模型训练的结果反映到读者偏好的读者-图书选择概率矩阵W，Wij表示在读者图书概率分布θ上读者u选择图书i的概率。据此建立起来的矩阵记录了任意读者对选择所有图书的选择概率。

为了提高预测结果的精准度，进一步采用聚类算法，根据图书的相关属性信息，对图书进行聚类。根据K-Means聚类算法在聚类效果中的良好表现，本文采用此方法实现图书的聚类。根据图书聚类的结果，对读者-图书选择概率矩阵进行裁剪，以此得到若干读者-图书选择概率子矩阵，缩小计算工作，仅在具有相似属性信息的读者-图书选择概率子矩阵中进行计算。

2.2 改进用户相似度

协同过滤算法的目的是找到和目标读者读书偏好相似的读者集合，根据读者-图书选择概率矩阵计算读者相似度，这是协同过滤算法关键步骤，影响着最终推荐结果的精准度。基于传统协同过滤算法读者相似度计算依赖于读者对图书的共同评分，但忽略了已评分图书的权重问题以及随时间变化读者图书偏好改变的可能性。例如：3个读者对同一图书有着相同的评分行为，读者1和读者2共同评分的图书发生在同一时间段内，而读者2和读者3共同评分的图书发生并不在一个时间段内，显然，读者1和读者2应比读者2和读者3有更高的相似度，然而，忽略了时间因素，利用传统协同过滤算法得到了相等的结果。

考虑时间因素对读者图书偏好的影响，为了提高读者相似度计算的精准度，引入时间因子sigmoid函数，函数值作为评分时间影响权重，评分时间越接近的读者，其相似度也就越高，计算式如公式(1)：

(1)

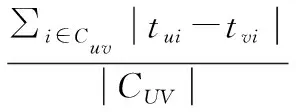
考虑时间因素对读者偏好相似度的影响，本文在皮尔逊相关系数基础上引入时间因子Sigmoid函数，得到改进后的读者相似度,如式(2)。

Simuv=Suv×Wuv=

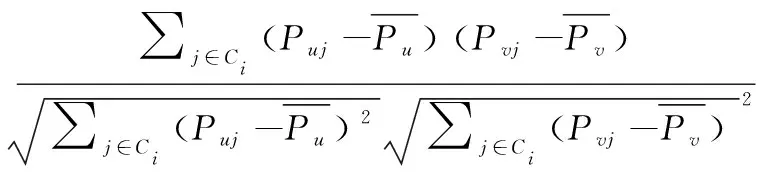
(2)

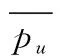
根据改进后的读者相似度计算公式完成相似度计算后，对结果进行排序，选择相似度最高的k个读者作为目标读者的邻居读者。

2.3 预测评分

在目标读者i的读者-图书选择概率子矩阵中，计算目标读者u对目标图书i的预测评分，如式(3)。

(3)

得到目标读者对未选择图书的预测评分后，根据评分由高到底排序，将评分最高的前k个图书推荐给该读者。

3 实验分析

3.1 实验数据

本文采用商丘职业技术学院图书馆信息化管理中心提供的数据集进行实验，在此数据集中，读者对自己看过的图书进行了评分，每位读者评分数不少于20条，评分结果为很好、好、一般、差、很差，分别记做整数5、4、3、2、1。分值高低反映了读者对图书满意度的高低。此数据集记录了2016年8月30日～2017年1月5日其间，1 351位读者对2 405本图书的143 000个评分，此数据集原始读者-图书评分矩阵稀疏度为92.8%。

3.2 评价指标

/N

(4)

得出的结果平均绝对偏差越小，推荐精准度越高，效果越好。

3.3 实验结果

将本文提出的ICF推荐算法与传统的基于内存的协同过滤算法进行对比，通过余弦夹角相似度、修正余弦夹角相似度和皮尔逊相关系数等3 种相似度度量方法作为比较，目标读者最近邻个数分别为(10，20，30，40，50)，得出的MAE值，如图2所示。

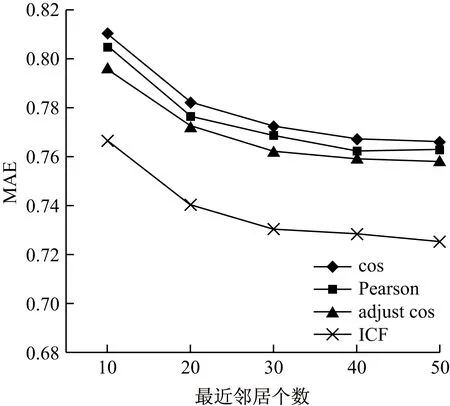
图2 ICF与传统的协同过滤算法比较

3.4 实验分析

实验表明，3 种传统的协同过滤算法相比较，余弦相似度的MAE值均最大，皮尔逊相关系数MAE值均居中，修正余弦相似度MAE值均最小，表明修正算法的有效性，而本文提出的ICF推荐算法，MAE值均最小，明显优于其它3种传统的协同过滤算法，说明引入时间影响因子权重反映读者图书兴趣变化的ICF推荐算法能够得到更好的推荐效果。

4 总结

为提高数据稀疏环境下图书推荐的质量，提出了一种基于LDA的改进协同过滤推荐算法，基于LDA主题模型得到读者-图书选择概率矩阵作为计算读者相似度的原始数据。为了更加准确地寻找读者邻居，本文根据图书属性对图书进行聚类，在聚类内部计算相似读者，并根据读者评分时间设计一种基于时间因子权重的读者相似度计算公式，更加准确地评估目标读者的邻居读者集，从而更准确地预测读者对图书的评分。最后，利用商丘职业技术学院图书馆信息化管理中心提供的数据集开展实验，实验结果表明，本文提出的方法，比基于余弦相似度、皮尔逊相似度的协同过滤算法更加精准，能有效提升图书推荐效果。