考虑楼板影响的RC框架结构连续性倒塌动力响应分析
罗维刚,黑晓丹,刘纪斌,李晓璐
(1. 兰州理工大学 土木工程学院,甘肃 兰州 730050; 2. 兰州理工大学 甘肃土木工程防灾减灾重点实验室,甘肃 兰州 730050; 3. 甘肃省水利水电勘察设计研究院有限责任公司,甘肃 兰州 730000)
0引 言
结构连续性倒塌被定义为:“由于局部破坏最终导致整个结构的倒塌或与初始破坏不成比例地破坏”,自2001年纽约世贸大厦遇袭倒塌之后,结构抗连续倒塌研究一直备受重视,很多国家相继颁布了结构抗连续倒塌设计规范[1-2],中国规范中也加入了相关条文[3],很多学者开展了相关研究。
Qian等[4]通过试验研究带楼板考虑抗震设计、带楼板不考虑抗震设计、不带楼板考虑抗震设计和不带楼板不考虑抗震设计4种工况在角柱失效下的动力响应,结果表明钢筋混凝土(RC)楼板和抗震设计可以增大试件屈服强度和初始刚度,能显著提高试件延性。Orton等[5]研究了一个1∶4缩尺比例的两层两跨缩尺模型中柱失效情况下结构的动力响应,并与单自由度模型的分析结果进行了比较,得出悬链线作用能够提高结构抗连续倒塌能力。梁益等[6]通过试验研究了在中柱失效的情况下带楼板和不带楼板的框架子结构破坏模式,试验表明楼板能显著提高子结构的峰值抗力(提高幅度达到45.6%),楼板对于提高结构在整个倒塌过程中的抗力有显著作用,且对提高悬链线效应有扩大作用。结构连续性倒塌的非线性动力拆柱法考虑了材料和几何非线性,能比较真实地反映结构的倒塌,而Qian等[4-6]在研究中并未采用非线性动力拆柱方法。Liu等[7]分别采用非线性静力和非线性动力拆柱法拆除内柱、边柱,研究了板柱结构抗连续性倒塌的能力,结果表明:失去边柱对结构破坏更大;动力非线性拆柱法比静力非线性拆柱法更容易造成结构连续倒塌,压膜效应对板柱结构抗连续倒塌性能有提高作用。Liu等[7]研究的板柱结构连续性倒塌对于钢筋混凝土框架结构不具代表性。目前对结构连续性倒塌的研究大多集中于静态响应研究,有关拆柱时间和初始状态对结构连续性倒塌动力响应影响的研究较为缺乏。
本文以有限元软件ABAQUS为平台,采用DOD 2010和GSA 2003规定的非线性动力分析法[8],即“①拆除构件前,结构在竖向荷载作用下达到静力平衡;②迅速拆除目标构件,拆柱时间不大于剩余结构周期的1/10;③进行非线性动力分析直至结构破坏或达到一个稳定状态”,分别分析了RC框架结构在角柱失效情况下楼板对剩余结构动力响应的影响,以及在考虑楼板影响情况下,角柱的失效时间和初始状态对剩余结构动力响应的影响。
1模型简介
采用简化的单自由度模型(图1),该模型采用如下假设:①仅考虑结构位移时程曲线从开始到最大部分,因为其余部分的位移时程曲线不能体现剩余结构连续性倒塌行为;②不考虑阻尼的影响;③所采用的抗力函数不考虑结构初始状态的影响[4]。

图1简化单自由度模型Fig.1Simplified SDOF Model
结构的动力响应是通过动力平衡方程求解实现的,对于单自由度体系,在外部荷载作用下,其动力运动方程为[9]
(1)

广义等效质量可以用如下公式表示[8]
(2)
式中:m(z)为分布荷载函数;ψ(z)为形状函数;mk为在zk位置处的集中质量;ψ(zk)为在zk位置处的形状函数值。
Yu等[10]指出相较于爆炸响应,连续性倒塌的发生时间短暂,阻尼所消耗的能量也微乎其微,一般分析中是不考虑阻尼影响的。
本文采用适用于配筋复杂的大型结构的组合式模型,模型中梁柱采用纤维梁模型,楼板采用分层壳模型。分层模型法在理论上最准确,能够很好地模拟框架结构在地震作用下的响应,在结构抗连续性倒塌研究中的准确性也已经被证实[11]。
模型中混凝土和钢筋的本构模型分别采用陆新征课题组开发的PQ-Fiber材料库中忽略混凝土抗拉强度的模型Uconcrete01和再加载刚度按Clough本构退化的随动硬化单轴本构模型USteel02。利用ABAQUS软件提供的用户材料子程序接口UMAT,将材料模型嵌入到PQ-Fiber材料库中。
2试验验证
2011年清华大学先后进行了框架柱、梁柱节点、三层四跨框架(图2)的拟静力倒塌试验研究,并且公布了全部试验和数值模拟结果[12]。本文选取的模拟对象为三层四跨框架,混凝土和钢筋的材性参数见文献[11]。楼板采用S4R分层壳模型,梁柱采用B31纤维梁模型,混凝土和钢筋分别采用PQ-Fiber材料库中Uconcrete01和USteel02。提取该框架的顶层位移和基底剪力,得到的数值模拟值与试验值对比如图3所示。可以看出,模拟曲线与实测曲线基本吻合,能够较好地模拟钢筋混凝土框架结构承载力、刚度变化以及滞回捏拢行为,但在加载位移幅值较大时模拟曲线较实测曲线略显饱满,且对强度退化现象反映不足。总的来说,通过纤维梁-分层壳模型可以较为精确地模拟结构中的材料属性、接触设置以及边界条件等,并论证了数值模型的准确性。本文采用Uconcrete01和USteel02本构关系在一定程度上可对钢筋混凝土框架结构的受力行为进行较好的预测。

图2钢筋混凝土框架试验Fig.2RC Frame Test

图3低周往复加载计算结果与实测结果对比Fig.3Comparison of Calculation Results and Measured Results of Low Cyclic Loading
3动力响应分析

图4模型三维视图Fig.43D View of Model
根据《混凝土结构设计规范》(GB 50010—2010)[3]和《建筑抗震设计规范》(GB 50011—2010)[13],使用PKPM设计一个六层RC框架结构(图4),短跨方向和长跨方向分别为3跨和6跨,跨度均为6 m,层高3.6 m。柱截面尺寸为550 mm×550 mm,梁截面尺寸为300 mm×500 mm,层高3.6 m,楼板厚度均为120 mm,设防烈度为8度,场地类别为Ⅱ类,抗震等级为三级,设计基本地震加速度为0.2g(g为重力加速度),设计基准周期为50年,混凝土采用C30,钢筋采用HRB400。
3.1楼板对连续性倒塌动力响应影响
分别建立3个数值模型:①带楼板RC框架;②不带楼板RC框架;③不带楼板将楼板质量以质量元形式分布到楼板四周梁上的RC框架。3个模型除对楼板做不同的处理外其余与上节带楼板RC框架一致。3个模型竖向应变云图如图5~7所示,3个模型分析步和计算方法设置相同,角柱拆除通过“生死单元”技术实现,分别提取角柱拆除稳定后3个模型的竖向位移、速度和加速度时程曲线,如图8~10所示。表1为各模型参数竖向最大绝对值。
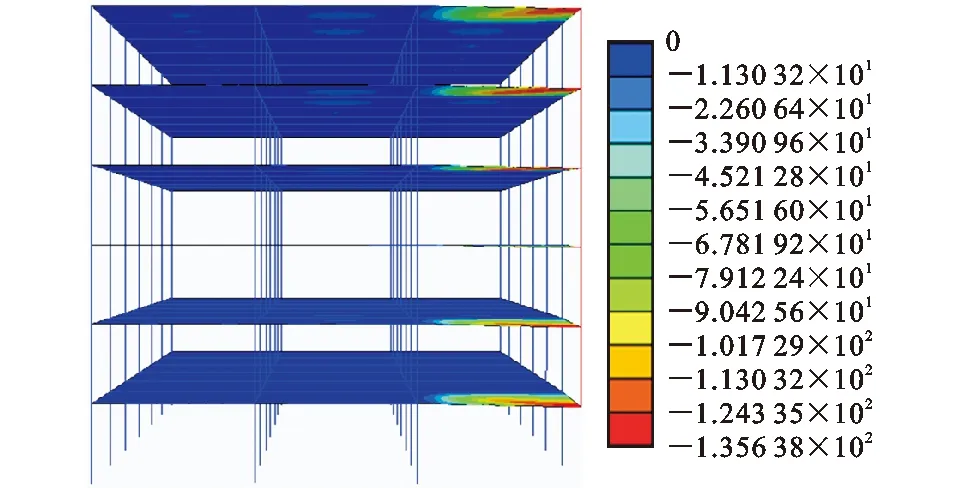
图5带楼板模型应变云图Fig.5Strain Contour of Model with Slab

图6不带楼板模型应变云图Fig.6Strain Contour of Model Without Slab

图7不带楼板加质量元模型应变云图Fig.7Strain Contour of Model with Mass Slab

图8不同模型位移时程曲线Fig.8Displacement Time History Curves of Different Models
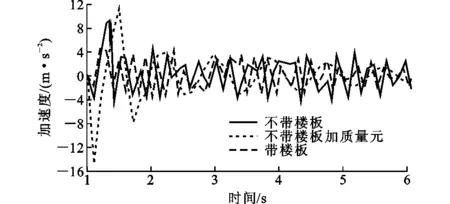
图9不同模型加速度时程曲线Fig.9Acceleration Time History Curves of Different Models

图10不同模型速度时程曲线Fig.10Velocity Time History Curves of Different Models
分析图8~10和表1,比较加楼板质量元、不带楼板、带楼板的模型,对比各自的位移、加速度和速度时程曲线,得出其竖向位移、竖向加速度和竖向速度从大到小依次均为:不带楼板加质量元、不带楼板、带楼板。带楼板模型最大位移响应比不带楼板最大位移响应小43.5%;不带楼板最大位移响应比不带楼板加质量元最大位移响应小66%。带楼板模型最大加速度响应比不带楼板最大加速度响应小38.4%,不带楼板最大加速度响应比不带楼板加质量元最大加速度响应小37.7%。带楼板模型最大速度响应比不带楼板最大速度响应小43.1%,不带楼板最大速度响应比不带楼板加质量元最大速度响应小27.6%。

表1各模型参数竖向最大绝对值Tab.1Vertical Maximum Absolute Values of Parameters in Models
注:|A|max为竖向最大绝对加速度;|V|max为竖向最大速度; |U|max为竖向最大位移。
可见,楼板对RC框架模型的抗连续性倒塌能够起到显著的提高作用,带楼板的RC框架模型动力响应都明显小于不带楼板的纯RC框架模型和不带楼板加质量元的RC框架模型。将楼板质量以质量元的形式分布到楼板四周梁上,忽略楼板的拉结作用,仅考虑其质量,更有效证明楼板的拉膜效应对结构抗连续性倒塌有着不容忽视的作用。
3.2拆柱时间对连续性倒塌动力响应影响
将结构的外部荷载和节点划分为3个阶段[4]:①角柱拆除前结构的重力荷载通过转移,对该角柱失效点(下文简称“失效点”)施加了一个等效的外部荷载,此时由于角柱尚未拆除,对结构的竖向位移造成约束,失效点的反力和外部荷载值大小一致,处于静态平衡;②角柱拆除阶段0
假定体系初始位移和初始速度均为0,当t>Δt时,失效点处于恒荷载作用阶段,此时失效点的动力效应可以用下列公式表述[14]。
利用Duhamel积分得位移udy(t)为

(3)
求得最大位移udymax为
udymax=ust[1+|sin((πT/Δt)/(πT/Δt))|]
(4)
则有
D=1+|sin((πT/Δt)/(πT/Δt))|
(5)
式中:P0为恒载;w为自振频率;ust为静位移。
可见结构最大位移取决于拆柱时间与结构自振周期的比值。采用非线性动力分析方法,考虑楼板作用,分别设角柱失效时间tf为0.025T,0.075T,0.1T,0.25T,0.5T,0.75T,T和1.5T,分析采用能够模拟构件失效的Newmark-β动力隐式法,使用Newton-Raphon法进行迭代计算[9]。分别提取失效柱顶点的竖向位移、加速度和速度时程曲线,如图11~13所示。提取不同拆柱时间结构的最大竖向位移、最大竖向速度和最大竖向加速度,如表2所示。由表2得出:当小于0.25T时,拆柱时间对结构的动力响应影响显著且越小影响越大;拆柱时间在0.25T~T之间时,随拆柱时间增大,结构动力响应变化呈减小趋势;当拆柱时间大于T时,结构的动力响应随拆柱时间增加呈收敛趋势。因此,柱失效时间越小对结构抗连续性倒塌危害越大,通常以非线性动力分析法分析连续性倒塌时,拆柱时间一般取小于剩余结构周期的1/10,美国GSA 2003和DOD 2010也规定,采用非线性动力法分析结构连续性倒塌时柱失效时间不得小于剩余结构周期的1/10。

图11不同角柱失效时间的位移时程曲线Fig.11Displacement Time History Curves at Different Failure Time of Corner Column
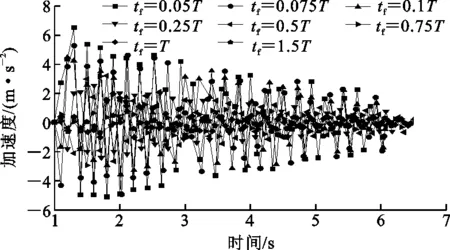
图12不同角柱失效时间的加速度时程曲线Fig.12Acceleration Time History Curves at Different Failure Time of Corner Column

图13不同角柱失效时间的速度时程曲线Fig.13Velocity Time History Curves at Different Failure Time of Corner Column
3.3初始状态连续性倒塌动力响应影响
结构的初始状态包括初始位移、初始速度、初始变形、初始荷载(外荷载)和阻尼等,通常对结构连续性倒塌的分析都假定结构的初始状态为0,这些与爆炸、冲击等突发情况造成的结构连续性倒塌非零初始状态都不符。由于爆炸、冲击等偶然荷载造成的结构柱破坏与在破坏的结构柱顶点施加竖向非零初始速度和初始位移非常相似,这些非零的初始状态影响着结构的动力响应。

表2不同拆柱时间对应的参数竖向最大绝对值Tab.2Vertical Maximum Absolute Values of Parameters Corresponding Column-removal-time
根据Nanci和Shalva[15]单摆模型,考虑初始位移u0和初始速度及不考虑和考虑阻尼时的结构位移响应u表达式分别为
u=u0cos(wt)+v0sin(wt)
(6)
u=[u0cos(wDt)+u0ξwsin(wDt)/wD]e-ξwt
(7)
(8)
不考虑初始速度仅考虑初始位移时以及不考虑和考虑阻尼时结构位移响应表达式分别为
u=u0cos(wt)
(9)
(10)
式中:v0为初始速度;e=2.72;ξ为阻尼比。
本文分别建立了考虑不同初始速度和不同初始位移的2组带楼板数值模型,角柱失效时间设为0.1T,分析其初始状态对结构动力响应的影响。规定初始向上的位移和速度为负,向下的为正。
比较图14,15得出:这些非零的初始状态影响着结构体系的动力响应。对于结构连续性倒塌,向上的初始位移比向下的初始位移对结构的破坏更严重,向上的初始位移越大,结构的竖向变形越大,这是由于向上位移引起的附加应变能最终会被向下的位移引起的应变能消耗。相比而言,初始向下的位移有助于减小结构最大竖向位移。这是因为初始向下的位移已经引起结构向上的抵抗力,使得在结构发生向下位移阶段的有效荷载变得越来越小,结构动力响应更缓和。同样,向上的初始速度比向下的初始速度对结构的破坏更严重,结构向上的初始速度越大,则竖向位移也越大。
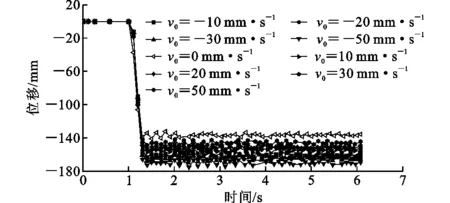
图14不同初始速度的时间-竖向位移曲线Fig.14Time-vertical Displacement Curves with Different Initial Velocities

图15不同初始位移的时间-竖向位移曲线Fig.15Time-vertical Displacement Curves with Different Initial Displacements
4结语
(1)通过对比带楼板、不带楼板和不带楼板加质量元3个RC框架模型,发现3个模型动力响应从大到小依次为不带楼板加质量元、不带楼板、带楼板,楼板的参与能够显著提高结构的抗连续倒塌能力,不带楼板模型竖向位移比带楼板的大43.5%,可见楼板在结构抗连续倒塌设计研究中的作用不容忽视。
(2)使用非线性动力分析方法,分别取0.05T,0.075T,0.1T,0.25T,0.5T,0.75T,T和1.5T的拆柱时间,研究发现,当拆柱时间小于0.25T时,剩余结构的动力响应变化幅值最为显著,破坏最严重;当拆柱时间为0.25T~T时,剩余结构动力响应变化幅值趋于平缓,当拆柱时间大于T时,剩余结构动力响应幅值基本无变化,趋于收敛状态。美国GSA 2003和DOD 2010规定“使用非线性动力分析方法研究结构连续性倒塌时,柱失效时间不得大于剩余结构自振周期的1/10”,根据本文研究结论,当拆柱时间小于0.25T时,拆柱时间对剩余结构动力响应影响显著,使用0.1T能够满足结构抗连续倒塌的设计研究。
(3)对比不同初始位移和初始速度状态下结构的变形,发现以往不考虑初始状态的结构连续性倒塌分析低估了初始状态对结构的变形影响,结构向上的初始位移和初始速度对结构的连续性倒塌有着不利的影响,而向下的初始位移和初始速度有着有利的影响。

