相关系数及其计算与分析研究
周丽霞

摘 要:本文给出了函数关系和相关分析概念,并通过研究总结了相关系数的含义,通过对相关系数公式的研究,给出了相关系数的简捷公式,同时进行了举例应用,已证明其实用性。
关键词:函数关系 相关系数 相关分析 积差法
无论是在自然界还是在社会经济领域,客观现象总是普遍联系和相互依存的,客观现象之间的数量关系可分为两种类型:函数关系与相关关系。
函数关系是指客观现象之间存在的、严格依存的、确定的数量关系。例如:某商品的销售量和销售价格与该商品销售收入之间的关系可以用来表示。相关关系是客观现象存在的一种非确定的相互依存关系,即自变量的每一个取值,因变量由于受随机因素影响,与其所对应的数值是非确定性的。由于影响一个变量的因素很多,而其中一些因素还没有被人们所完全认识和掌握,或是处于已经认识但对其产生的影响还不能完全控制和测量;另外,有些因素尽管可以控制和测量,但在操作过程中或多或少都会有误差,所以在复杂的社会系统中,各种事物或现象之间的联系大多体现为相关关系,而不是函数关系。
相关分析的主要目的就是要在错综复杂的客观现象中,通过大量观察统计资料,对现象间相互关系的密切程度和变化规律,有一个具体的数量观念,并进一步找出相互关系的模式,以便进行统计预测和推算,为推算未知和预测未来提供数据,为制定计划、决策提供资料。
相关关系的判断方法主要有相关表(表格法)、散点图(图示法)、相关系数法。
通过相关表和相关图可以明确、直观地判断两个变量间有无关系,并对变量间的关系形态作出大致的描述,但不能准确反映变量之间关系的密切程度。因此在初步判定变量间存在相关关系的基础上,通常还要计算相关关系的度量指标——相关系数。
(一)相关系数的含义
相关系数是指在直线相关条件下,说明两个现象之间相关关系密切程度的统计分析指标,通常用r表示。
相关系数的取值范围在-1和+1之间,即-1≤r≤1。如果相关系数r=±1,表示两个现象完全相关,它们之间存在确定的函数关系;如果相关系数r的数值越接近于1(+1或-1),表示相关关系越强;如果相关系数r的数值越接近于0,表示相关关系越弱;如果相关系数r=0,表示两个现象完全不相关(仅指不是直线相关);如果相关系数r>0,表示正相关;如果相关系数r<0,表示负相关。
但需要注意的是,r只表示x与y的直线相关密切程度。当 很小甚至等于0时,志宁表示x与y 之间不指向相关,并不表示x与y之间就不存在其他非直线类型的相关关系。
为了在判断时有个标准,现介绍一种常用的相关关系密切程度的划分标准:
在原始数据比较多时,计算出的相关系数 的绝对值在0.3以下是无直线相关,0.3以上是有直线相关,0.3 0.5是低度相关,0.5 0.8是显著相关(中度相关),0.8以上是高度相关。
按照上面的标准来判断,严格说要有一个条件,就是计算系数的原始数据要比较多,如果数据太少,判断相关的密切程度需要查相关系数检验表来判断。
(二)相关系数的计算公式
在未分组资料条件下
1.相关系数的定义公式。
公式(1)
式中,
协方差σxy 的作用:
(1)协方差显示x与y是正相关还是负相关。
相关系数的正负性完全由协方差的正负性决定。协方差为负,则相关系数为负,相关关系是负相关;协方差为正,则相关系数为负,相关关系是正相关。
(2)协方差显示x与y相关程度的大小
当标准差σx 和σy 为定值时,协方差σxy 的绝对值越小,表示x 与y的相关程度越低;协方差σxy 的绝对值越大,表示x 与y 的相关程度越高。
2.相关系数的“积差法”公式。
对公式(1)中的分子分母同时乘以n ,相关系数r 的公式可写成:
由于公式(2)是通过将各个离差相乘的方法来说明相关程度的,所以通常把这种相关系数的公式叫做“积差法”,积差法是计算相关系数的基本方法。
相关系数的定义公式是根据x 与y 的数值计算的,当x 或y 的值为除不尽的小數时,计算既麻烦又影响其准确性。在实际工作中,如果根据变量的原始数值计算相关系数,可运用简捷法计算公式。
3.相关系数的简捷公式。
公式(3)不用计算两个变量的平均值与标准差,既减少工作量,又可以减少计算平均值除不尽所带来的误差。
(三)相关系数的计算举例
[例1]对一公司的10名职工的月消费支出和可支配收入进行调查得到如下原始资料(元),根据相关资料计算职工月消费支出和可支配收入相关系数(见表1)。
解:根据相关资料列出职工消费支出和可支配收入相关系数计算表(见表2)。
将有关数据代入计算公式,可计算出相关系数:
答:相关系数0.984>0.8,接近1,说明职工月消费支出和可支配收入为高度正相关关系。
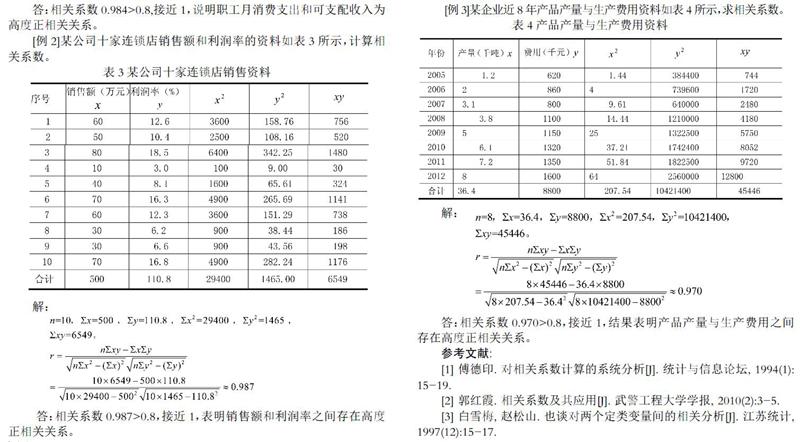
[例2]某公司十家连锁店销售额和利润率的资料如表3所示,计算相关系数。
解:
答:相关系数0.987>0.8,接近1,表明销售额和利润率之间存在高度正相关关系。
[例3]某企业近8年产品产量与生产费用资料如表4所示,求相关系数。
解:
答:相关系数0.970>0.8,接近1,结果表明产品产量与生产费用之间存在高度正相关关系。
参考文献:
[1] 傅德印. 对相关系数计算的系统分析[J]. 统计与信息论坛, 1994(1):15-19.
[2] 郭红霞. 相关系数及其应用[J]. 武警工程大学学报, 2010(2):3-5.
[3] 白雪梅, 赵松山. 也谈对两个定类变量间的相关分析[J]. 江苏统计, 1997(12):15-17.

