基于混合蛙跳算法优化神经网络的齿轮箱故障诊断研究

王宇

（临汾职业技术学院，山西临汾041000）

0 引言

机械设备在人类的生活生产中饰演重要角色，而在实际生产中，设备的突发故障时有发生，机械设备一旦出现事故，将带来巨大的经济损失和人员伤亡[1]。因此，机械设备的安全可靠运行就成为生产的关键一环。同时，在现代制造业的强劲发展中，催生出智能机器并迅速被大规模普及应用，而能够在恰当的时候对机器进行保养和维护就成为生产中的重要一环，利用监测检测系统对机械设备的运行情况进行检测或快速故障诊断，以提高设备使用效率，降低维修成本[2]。

对机械系统进行状态监测与故障诊断的课题一直广受关注。齿轮箱作为众多机械设备的重要部件，在航空、船舶、风电等工业设备中广泛应用，作为关键部件之一，其运转状况对设备的正常运行具有较大影响。因此研究人员不断尝试，探索出小波降噪与Hilbert解调相结合的故障诊断方法[3]、VMD和多参数融合的故障诊断[4]等许多技术。本文以齿轮箱作为研究对象，提出基于混合蛙跳优化神经网络的齿轮箱故障诊断方法，并通过对比实验验证该方法的准确性和稳定性。

1 混合蛙跳算法优化神经网络

1.1 人工神经网络

BP神经网络算法简洁、易实现，是一种成熟且应用广泛的训练模型[5]。由于其主要采用最速下降法，并根据梯度下降法修正权值[6]，以实现误差函数的最小，故BP网络存在两个主要问题：1）训练效率较低，收敛速度慢；2）易陷入局部最优[7]。

1.2 混合蛙跳算法

蛙跳算法是一种启发于自然界生物觅食行为的寻优计算方法，该算法融合了种群局部搜索与全局信息共享，各模因组进行“构建-混合-再划分”的迭代过程，从而实现全局信息共享。通过采用这种平衡策略，可以避免陷入局部最优的“陷阱”，找到全局最优解，故混合蛙跳算法具有跳出局部极优的特点[8]。图1为混合蛙跳算法流程图。

图1 混合蛙跳算法流程图

1.3 SFLA-BP网络模型

将混合蛙跳算法用于对神经网络的训练，利用混合蛙跳算法的优势，解决BP网络算法学习效率低、易出现局部极值、优化结果受初始条件限制等一系列问题。

2 SFLA-BP网络模型在齿轮箱故障诊断中的实验及分析

2.1 采集齿轮箱振动信号

使用压电加速度计、36通道动态信号数据分析系统等装置采集齿轮箱的振动信号，测得齿轮箱在正常工况、断齿、滚动轴承保持架断裂、滚动轴承外圈裂纹、复合故障（轮齿断裂和轴承外圈裂纹复合故障）等5种工况下的数据，利用小波分析对振动信号作去噪处理[9]。信号的采样频率，输入轴的转速为1200 r/min。

2.2 选取齿轮箱故障特征参数

不同的时频域指标只能在一定程度上，反映设备处于某种运行条件下的个别工作状况[10]，例如当齿轮箱处于中后期故障时，波形指标表现出较好敏感性[11]；而峭度指标反映随机变量的分布特征，无量纲参数对零件的前期故障具有较高的预测性[12]。因此，针对各指标的特性，考虑其对故障的分辨能力，同时结合课题研究对象，通过大量实验，我们将波形指标、裕度指标、峭度指标、偏态指标、偏度系数、频谱重心、频域方差、相关因子[13]等8个有效特征作为探究齿轮箱故障的特征参量。

2.3 神经网络的样本数据及标准输出

为确保实验的有效性和一般性，对于采集到的齿轮箱5种工况下的振动加速度信号[14]，通过对比，选择多组具有代表性的原始信号，对其进行去噪处理，然后将每一种工况下的振动信号分为4段，并求取各段信号的峭度指标等8个特征值，因此，从每一路信号中可以得到4组数据[15]。最后，统计并归纳计算所得数据，将4组数据中的前2组数据设定为训练样本，后2组数据作为诊断样本，构成实验研究的数据样本，用于检验训练后的SFLA-BP算法模型对齿轮箱故障的诊断效果。标准输出值设置为：正常工况为（1，0，0，0，0），轮齿断裂为（0，1，0，0），轴承保持架断裂为（0，0，1，0）、轴承外圈裂纹为（0，0，0，1）、复合故障为（0，1，0，1）。

上述8个诊断指标中混杂着有量纲和无量纲数值，为便于各组样本数据间进行参照对比，按照式（1）进行数据归一化处理：

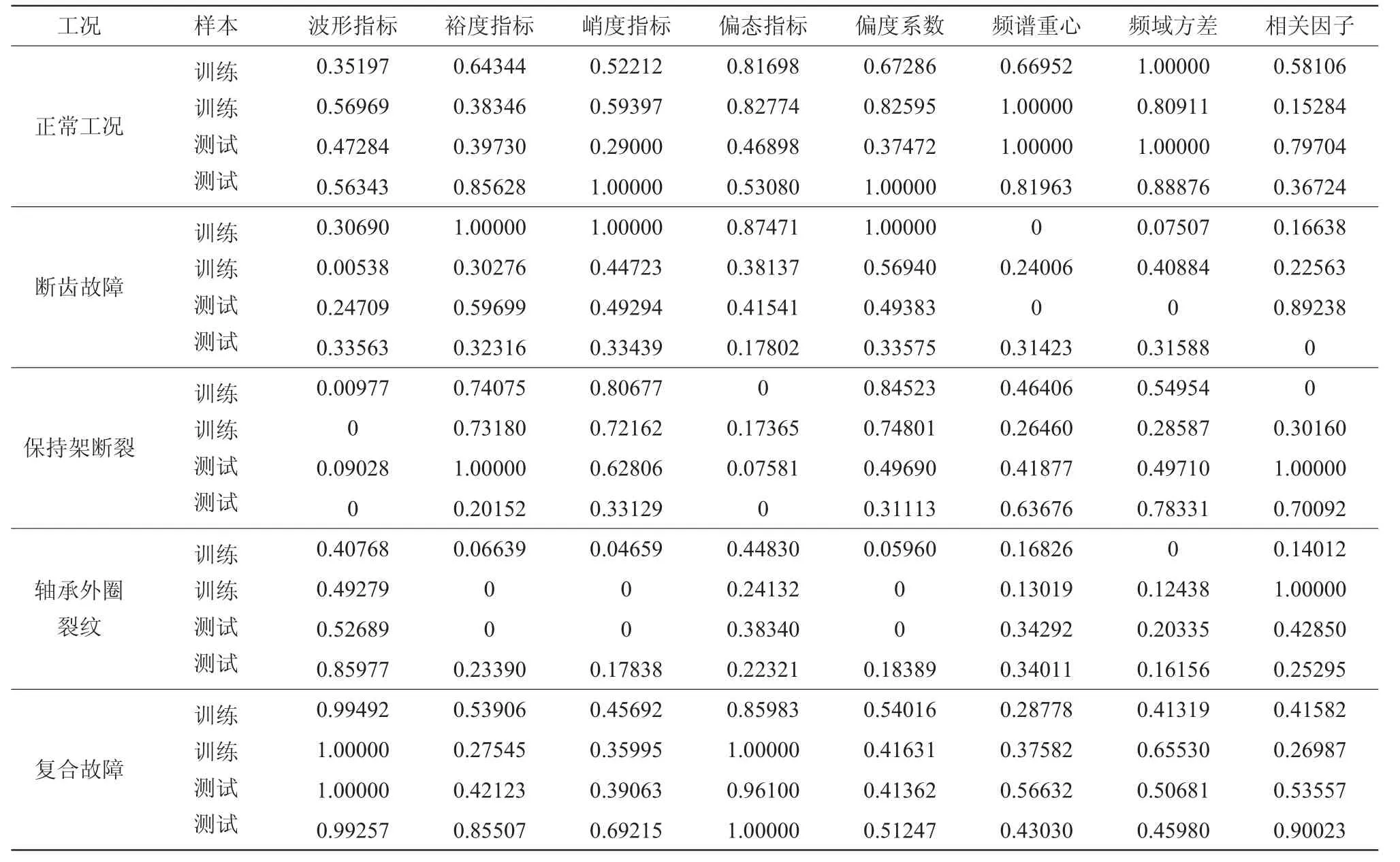
表1 归一化后的样本特征参数表

式中：xig表示归一化后的值；xi表示第i个特征参数；xmax、xmin分别表示xi中的最大值和最小值。表1为齿轮箱故障诊断研究中的归一化后的训练样本和测试样本。

2.4 SFLA-BP算法模型在齿轮箱故障诊断中的实现

BP神经网络结构和参数的设定：根据创建BP网络结构的指导原则，三层网络结构可以满足一般模式识别问题的要求[16]。对于三层BP网络，隐含层节点个数n2与输入层节点个数n1之间的关系应考虑应用的实际环境不同，需要经过实验不断调整寻找隐含层节点个数的最适值。

结合故障特征和经验结论，通过理论分析，以及多次实验验证，最终将BP神经网络的参数设置为：三层网络结构且各层神经元数为8-8-4。神经网络隐含层神经元的传递函数和输出层神经元的传递函数分别设为S型正切函数tansig、S型对数函数logsig，训练函数设为trainlm，训练次数定为1000，训练目标值为0.0001，学习速率为0.05。

SFLA参数设置：混合蛙跳算法用于快速探寻BP神经网络中的最优权值和阈值，假设每一个权阈值代表一只蛙个体，故蛙群体数N=108，模因组数mp=4，每组数量n=5，局部搜索次数lmax=10，全局混合迭代次数Gmax=100；并将蛙个体适应度设定为预测值与实际值的误差平方和函数。

对照模型：单纯BP神经网络模型。

2.5 仿真结果及对比分析

图2是SFLA-BP网络模型中种群最优值的收敛曲线图，曲线表示目标函数随迭代步数的变化情况，图中显示，迭代前期，目标函数急速收敛，随后目标函数值处于稳定状态，依靠算法的全局寻优特性，跳出局部极值，继续寻找最优值，在运行60次左右迭代后，算法对权阈值完成修正。

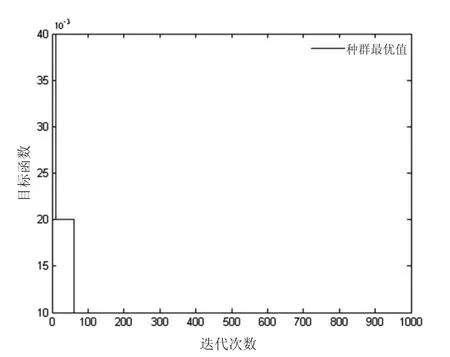
图2 混合蛙跳算法寻优过程

为验证SFLA-BP网络模型对诊断齿轮箱故障的高效性，本文以BP神经网络算法作为比照对象，其网络拓扑结构和相应参数的设置同SFLA-BP模型相同，利用同组齿轮箱工况数据对齿轮箱的5种状态进行诊断，并将诊断结果的准确性作为诊断方法的衡量指标，其收敛速度作为参照指标。为保证仿真结果的可靠性，多次反复进行论证，得到大量结果图组，其中SFLA-BP算法的结果图组中差异不大，运行结果稳定，可以准确分辨齿轮箱的5种模式；而BP神经网络算法的结果随机性较大，均存在较大程度的误差。现就多组实验结果中，选取一组具有代表性的结果，进行分析对比，如图3、图4所示，其中:图3为SFLA-BP神经网络模型对齿轮箱工况的诊断结果图;图4为BP神经网络的诊断结果图。

图3 混合蛙跳算法优化BP神经网络诊断结果

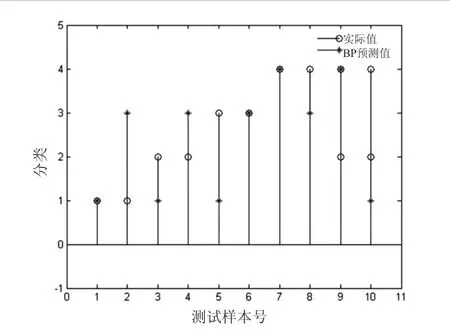
图4 BP神经网络诊断结果

在图3和图4诊断结果图中，圆圈代表理想值，星号代表实际输出值；图中横坐标代表样本序号，共10组测试样本；纵坐标代表齿轮箱的5种工况类别。现对理想输出值在图中的显示位置和方式进行简单介绍。由于本文对不同工况下的理想输出值进行了设定，如正常工况的序号为1，并设置为（1，0，0，0），即理想输出值中1出现的位置号代表工况的分类号（除复合故障），故第1号测试样本的理想输出值显示在图中的分类1号处；而复合故障由2号和4号故障混成，因此在图中的分类号2、4处均有显示。

图3和图4可以从定性的角度评价3种方法的诊断准确性。由于此2幅诊断结果图是从大量实验结果图中，经过综合考虑甄选出来，因此具有一般性和代表性。通过分析此2幅诊断结果对比图可知，SFLA-BP算法模型的诊断输出结果与期望输出一致，不仅能够准确识别齿轮箱的单一故障，而且对含有2种故障的复合故障也有较强的诊断能力；对于图4，即单纯采用BP神经网络进行故障诊断，其结果对比图中显示，无论是对于单一故障还是复合故障，该方法的诊断结果很不理想，通过分析所有利用BP网络诊断方法得到的诊断结果对比图，该方法的诊断结果波动较大，稳定性较差。

因此，通过对诊断齿轮箱故障的2种方法的定性分析，可以得出SFLA-BP算法模型对准确识别齿轮箱的单一故障和简单复合故障具有相对较高的可靠性。

3 结论

本文针对齿轮箱故障诊断课题，通过利用SFLA-BP算法模型诊断、识别齿轮箱的五种故障模式，同时设置BP神经网络算法模型为参照，对比实验结果发现，SFLA算法是一种高效的寻优方法，且混合而成的SFLA-BP算法模型对识别齿轮箱故障模式具有较高的准确度和较强的稳定性，表现出很好的应用性，特别是对诊断混合故障方面极具潜力，有待深入研究。