自锚式悬索桥索鞍预偏及顶推控制方法研究

牛登辉，蔡送宝

（1.天津市市政工程设计研究院，天津市 300051；2.天津市赛英工程技术咨询有限公司，天津市 300191）

0 引言

空缆状态是指索鞍预偏后架设于悬索桥上空缆的线形及内力状态。空缆状态分析可为架设主缆时提供理论空缆线形。空缆线形是索夹放样、吊索张拉和索鞍顶推的初始状态，是自锚式悬索桥能否达到设计成桥要求的前提条件[1]。一旦空缆线形有误是无法通过后期施工过程的调整而最终达到设计恒载成桥状态的，而索鞍预偏量的设置又影响空缆线形。因此确定索鞍预偏量对对应的空缆状态十分关键。

1 设置预偏量的原因及计算方法

设计恒载成桥状态边、中跨主缆水平分力相等，但中跨长度较长，总荷载较重，而边跨长度短、荷载轻。空缆状态时加劲梁等外荷载还没施加于主缆上（索夹、吊索等还没有施工），此时的主缆内力相当于设计恒载成桥状态的主缆内力减去了外荷载所产生的内力，显然中跨减小总量比边跨减小总量大得多，如果索鞍仍然处在设计恒载成桥状态的几何位置处时，会产生较大的不平衡力[1]。因此可能会发生如下情况：

（1）由于主缆丝股张力太大，因而将克服索鞍槽内的摩擦力而发生滑动，造成施工极为困难，无法保证架设精度。

（2）索鞍的固定限位装置必须要有极高的限制位移的能力，因而造成施工复杂，临时费用高。

（3）桥塔在不平衡力作用下使得桥塔成为承受压弯作用的细长构件，从而使得桥塔施工状态极为危险。

因此需要在架设主缆之前就必须对主索鞍设置预偏量。计算预偏量数值的假设条件有：

（1）各跨间无应力索长与设计恒载成桥时无应力索长保持一致。

（2）在主缆自重作用下，中、边跨主缆张力的水平分力相等。

空缆状态下悬索桥主缆线形及方程[2-4]如下所示：

如图1所示为仅受到X、Y方向均布荷载的悬索。图中索段在其单元坐标系中起点坐标为（0，0），终点坐标为（l，h），水平荷载为 qx，竖向荷载为qy（沿跨度均布）。在索段微分单元中，微段起点的水平力为H，竖向力为微段终点的水平力为，竖向力为由微分单元的静力平衡条件得:

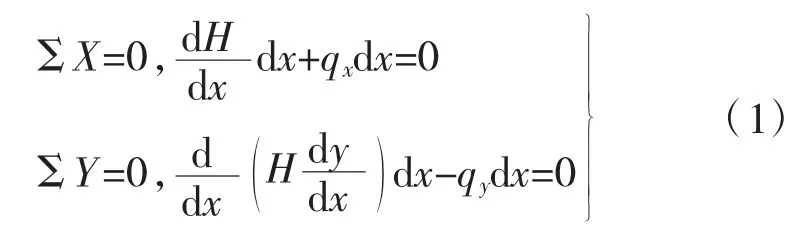
由式（1）中的后一方程得：

式（1）和式（2）为索段平衡微分方程，悬索桥索段的水平荷载qx=0，则根据式（1）得出张力水平分量为常量，因而式（2）又可以写成

q沿曲线s分布，则

qy为沿跨度分布荷载，由式（4）得：

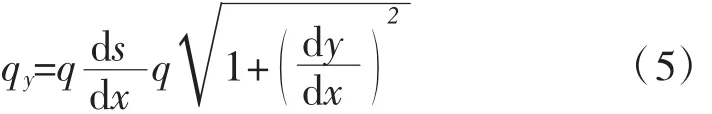
将式（5）代入式（3）有

根据边界条件

其中，

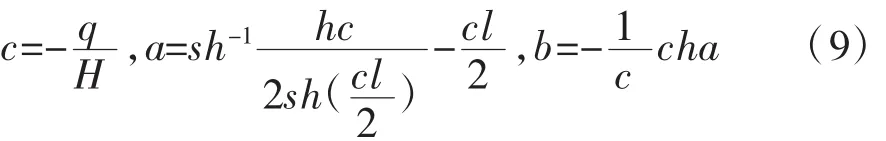
在计算空缆线形时必须考虑主梁的弹性压缩而增设预长量。假设空缆状态时桥塔顶端两主索鞍各向边跨方向预偏d，设计恒载成桥状态时中跨跨径为l中，边跨跨径为l边。且设中、边跨主缆索力水平分力为H，主梁弹性压缩为Δle，则空缆状态中跨跨径伸长为l中空=l中+2d，边跨跨径为l边空=l边+Δle-d。中、边跨各建立如图2所示的坐标系。

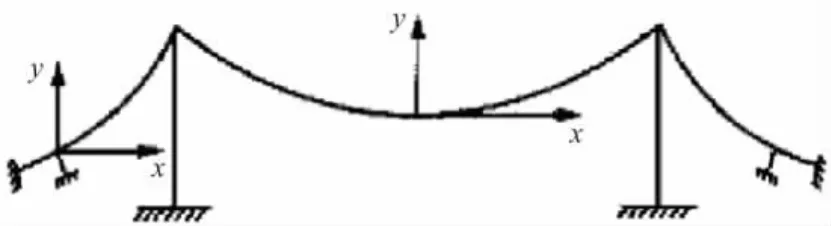
图2 悬索桥空缆状态示意图

对于中跨主缆线形悬链线方程式（9），由边界条件 x=0，y'=0 得 sha=0，则 a=0。

空缆状态中跨无应力长度为

对于边跨主缆线形悬链线方程式（9），由边界条件x=0，y=0得

由边界条件 x=l边空，y=h边空，得：

即空缆状态边跨主缆线形方程为

1.3 利用果蝇的蛹收集处女蝇 接种纯种亲本果蝇，当观察瓶壁上出现较多的黑褐色的蛹时，用干净解剖针轻轻地把黑褐色的蛹取出，单独放到10mL的塑料离心管里，置于温度25℃、湿度60%的培养箱里进行培养。每天观察，待果蝇羽化出来后进行麻醉，鉴别雌雄，收集处女蝇。

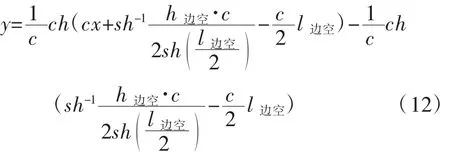
空缆状态边跨无应力长度为

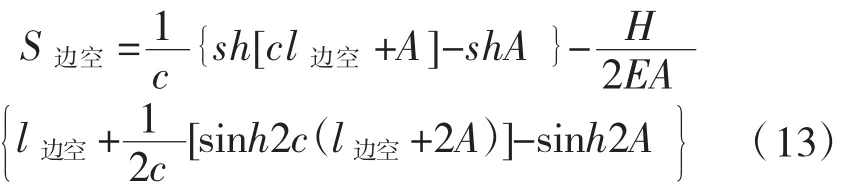
由于各跨间无应力索长等于成桥时无应力索长，于是有非线性方程组

Δle是由成桥和空缆两种状态共同叠代决定的，其量值又会影响到空缆线形，因此要采用叠代算法逐步逼近求解，使最终叠代得到的空缆线形与给定的参数相符，即由空缆状态和成桥状态联合求解计算出的量值与前次求得的量值之差在给定的误差范围内。其叠代算法如下：

（1）先假设参数Δle以及空缆状态的IP点位置（或主缆与索鞍的切点位置）；令

（2）假设塔顶偏移量d0。

（3）求解边、中跨主缆线形。

（4）计算Δle等。

（5）比较差别，若误差不可接受，则叠代（3）～（5）步骤，直至满足要求。

2 索鞍顶推原则

根据悬索桥在顶推时，结构的受力要求及合理性，在尽量减少顶推次数的基础上得出了以下顶推原则：

（1）必须保证施工期间的结构安全和足够的安全储备。

（2）由于顶推施工复杂，影响工期和施工费用，所以在保证施工安全的前提下，应该尽量减少顶推次数。

（3）在张拉某根吊索时，如果桥塔或其他构件的应力超限，则必须在前一阶段顶推一次（即插入顶推施工阶段）。一般大跨径悬索桥的顶推方案设计时，要求桥塔截面边跨侧必须具备1 MPa的压应力储备。

（4）在张拉某根吊索时，如果桥塔偏位超标，则必须在前一阶段顶推一次（即插入顶推施工阶段）。一般大跨径悬索桥的顶推方案设计时，要求桥塔朝中跨方向偏位小于最不利活载作用下的桥塔偏位值。

（5）在顶推施工阶段，应尽可能地加大顶推量，以减少顶推次数，但顶推后的桥塔截面中跨侧压应力储备和桥塔朝边跨方向偏位也必须满足（3）和（4）的要求。

3 桃花峪黄河大桥索鞍预偏及顶推计算

桃花峪黄河大桥位于郑州市与焦作市交界处，其中主桥为（160+406+160）m双塔三跨自锚式悬索桥（见图3），主梁采用整体钢箱梁，全宽39 m。主塔采用双柱门式混凝土塔。主缆采用公称直径5.3 mm、公称抗拉强度1 670 MPa的高强镀锌钢丝，为平面线形，布置在钢箱梁两侧，中跨的矢跨比为1/5.8。吊索采用公称直径5.0 mm、公称抗拉强度1 670 MPa的高强镀锌钢丝，基本间距为13.5 m，桥塔两侧的吊索距桥塔中心线14 m。两个边跨分别设置10对吊索，中跨设置29对吊索。该桥工程设计按双向六车道高速公路建设，设计速度100 km/h，设计荷载等级为公路-Ⅰ级×1.3[5]。

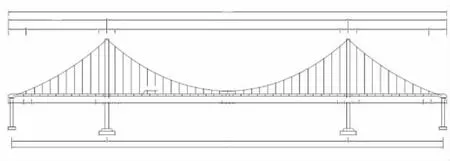
图3 桥型布置图

经计算桃花峪黄河大桥索鞍预偏量为70 cm（朝向河岸侧），对于桃花峪黄河大桥的主索鞍顶推方案（顶推次数、顶推时机和顶推量）进行了多方案比选，分别对不同的方案进行有限元数值仿真模拟。将压应力储备大、塔顶偏位小的方案选为最优方案。表1及图4～图6给出了四种施工顶推方案和相应的塔顶偏位（包括正负偏位）随施工阶段的变化情况。

图4 方案1塔顶偏位随施工阶段变化图

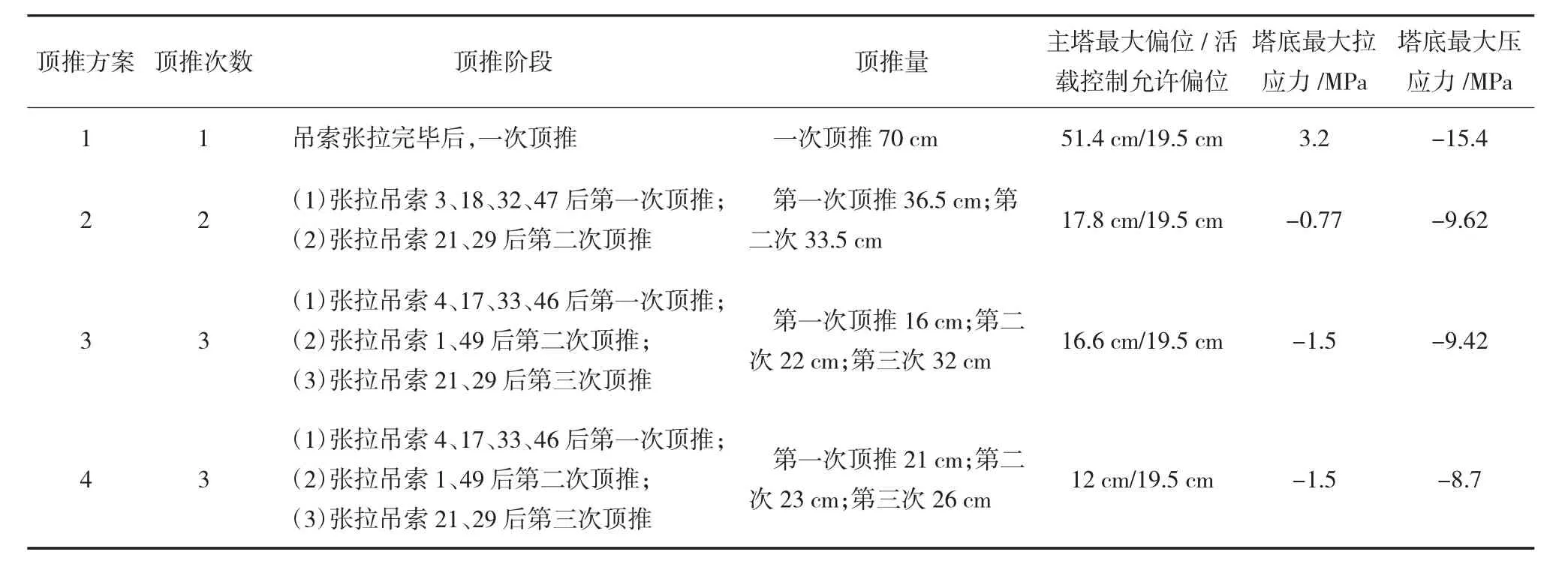
表1 顶推方案比较

图5 方案2塔顶偏位随施工阶段变化图

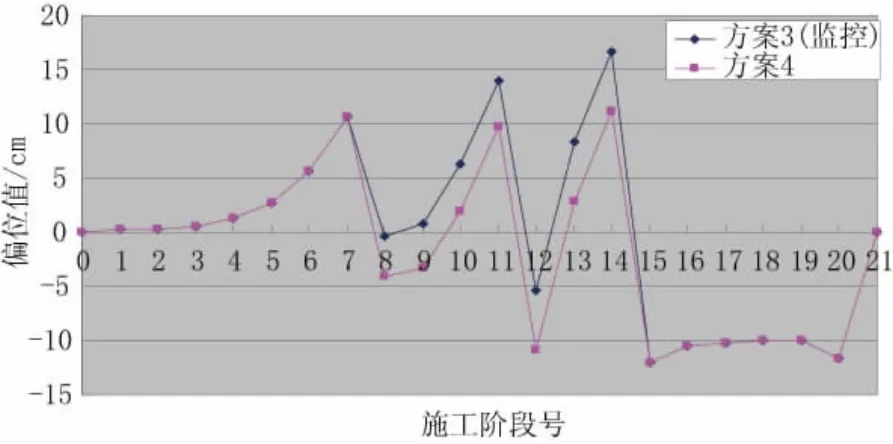
图6 方案3、4塔顶偏位随施工阶段变化图

根据上述索鞍顶推原则可知，顶推方案4为最优方案。

4 结语

本文以河南桃花峪黄河大桥为背景，围绕自锚式悬索桥索鞍预偏及顶推控制方法展开了研究工作。

（1）本文推导了自锚式悬索桥索鞍预偏量的解析算法并给出了体系转换过程中索鞍顶推原则。

（2）针对河南桃花峪黄河大桥，进行了四种施工顶推方案的比选，最终选定方案顶推次数少，塔顶偏位小。