考虑区域异质性的应急物资选址-分配优化
朱 莉,丁家兰,计梦婷
(南京信息工程大学 管理工程学院;中国制造业发展研究院,南京 210044)
面临重大灾害事件如何快速开展科学高效的灾后应急物资供给,以最大程度减少灾区人员伤亡和财产损失,是应急救援决策体系中需要解决的重要问题。灾后应急物资的供给决策常涉及两个关键任务[1]:在灾区附近选择建立临时救援中心,让来自各地供应点的救助物资在此集聚后再依照各灾区需求进行统一调度分配。这一过程被称为应急物资的选址-分配优化,有利于缓解应急救援系统可能出现的拥塞现象,实现应急救援体系整体的协调[1]。
物资的选址-分配(Location-Allocation Problem,LAP)是物流运营优化中的经典问题,多年来诸多学者从多目标决策[2-3]、随机约束[4]以及高效求解算法[5-6]等角度予以关注。而应急场景中的物资选址-分配相关研究,大多是关于灾前的计划布局决策,文献[7-9]中讨论在灾害准备阶段如何对应急物资实施科学的预先配置。也有部分研究关注灾后如何开展救援调配工作,马祖军等[10]讨论突发灾害后如何选择灾区附近仓库作为候选应急物流中心的问题,并探讨“灾区外围物资集散点至选定的应急物流中心再到灾区需求点”之间的物资合理调配优化。王海军等[11]考虑灾区需求和救援车辆运输时间的不确定,将机会约束规划方法应用于灾后配送中心的选址和救援物资的发放决策中。
无论灾前还是灾后,这些LAP相关文献基本都是在“多供给点-多受灾点”的普适场景下进行供给点的选择和供给点到受灾点的物资分配优化,较少有研究关注到重大灾害影响下各供给(受灾)区域实质存在的异质性特征。例如不同灾区受灾程度的差异会使得对救援物资的需求量不同;再如各供应点或救援物资配送中心(简称救援中心)由于所在区域的地理位置、经济水平和道路通达性等不同发达程度也会导致救援呈现差异化效应。这些现实存在的异质性因素需要被考虑到选址-分配优化中去,否则会影响应急决策方案的有效性。
基于此,本文选择以应急反应时间的差别为指征来反映各救援中心异质性特点,构造一个由救援中心所在区域经济发展水平、自然地理位置、物流发达程度、受灾害影响程度、综合交通可达性、基础设施竞争力以及应急政策关注度等因素组成的综合评价体系,用来评估各救援中心处应急反应时间的差别。并将此差异化时间因素作为反映不同救援时效性的决策度量集引入选址-分配优化中,结合各灾区不同受灾程度,最终构建了一个考虑区域异质性的应急物资选址-分配模型。通过设计并应用遗传算法对模型实施案例仿真求解,对关键参数进行敏感性分析以验证所构模型和算法的可行性和有效性,得出相关结论为政府部门的应急决策提供参考建议。
1 考虑区域异质性的应急物资选址-分配模型
研究问题的场景是某重大突发地质灾害的爆发使多个邻近区域均受到不同程度的影响,此处邻近区域大到可涉及多个邻省(市)、小到可指同一城市的多个划片区。如2008年汶川地震中四川省内极重灾区就涉及10个县(市)、较重灾区也有近30个、一般灾区更达100个县(市、区);再如,2010年青海玉树地震波及的范围约12个县3万km2,其中极重灾区约900 km2、875 km 公路几近瘫痪。探讨在不同程度的受灾区域附近选择建立多个临时救援中心,并分析从供应点到救援中心、救援中心到灾区的物资分配优化问题。
1.1 模型假设与符号说明
本文所构模型属于多中心选址问题,与单中心选址相比,用来解决多中心选址问题的研究方法有双层规划法、CFLP(Capacitated Facility Location Problem)法 和 Baumol-Wolfe 法 等[12]。 现 以Baumol-Wolfe法为基本原型进行模型的假设。
假设条件:
(1)供应点和备选救援中心的位置、数量均已知。
(2)考虑成本或资源约束,从所有备选点中选出一定数量来建立临时救援中心。
(3)在各备选点构建临时救援中心所需的固定成本已知。
(4)救援中心处对物资的处理成本是有关物资流量的凹函数,且其单位物资处理成本已知。
(5)讨论单种应急物资单次分配优化情形。
(6)使用同种运输方式、同种车型由供应点到救援中心、救援中心至灾区进行应急物资的运输,且单位物资运输成本的大小取决于两区域间的运输距离。
(7)不考虑各供应点间或各救援中心间物资的相互救助。
设i={1 ,2,…,I} 是应急救援物资分配系统中I个供应点的序号集合,j={1,2,…,J} 为J个救援中心备选点的序号集合,k={1,2,…,K}为K个受灾区域的序号集合。第i个供应点的总供应量用S i表示,选定第j个备选点建立救援中心的最大物资容量为C j,第k个受灾区域处的应急物资需求量为D k。
从供应点i到救援中心j的单位物资运输成本为c ij,相应的物资分配量为x ij。从救援中心j到灾区k的单位物资运输成本为c jk,相应的物资分配量记为y jk。zj是用来描述救援中心选择情况的0-1整数变量,z j=1表示第j个备选点被选中建立救援中心;否则,zj=0。在备选点j上建立救援中心的固定成本为gj,救援中心备选点j处对单位物资的处理成本(包括集散、装配等操作)用bj表示。救援中心备选点j处应急反应时间长短的区分用T j表示。α意味着在各救援中心做出应急反应的单位时间内可能造成的人员伤亡和财产损失,也可理解为单位反应时间-损失成本转换系数。
1.2 模型构建
模型决策问题是:从J个备选点中至多选择M个来建立救援中心,由多个供应点对选中的救援中心进行合理供给、并将这些救援中心的应急物资分别配送给K个灾区实施救助,使各灾区需求量均得到满足且分配的物资不超过各供应点和各救援中心的容量限制。

目标函数式(1)是最小化救援中心选址-物资分配系统的广义应急总成本,由物资从供应点被送至救援中心及从救援中心到灾区所耗总运输成本、建立多个救援中心所需花费的总固定成本、救援中心处对应急物资汇集分散的总处理成本(其中,W j为第j个备选救援中心处的总物资流量,θ为体现物资规模的流量指数,0<θ<1)以及救援中心处对灾害实施应急反应的时间损失成本4类成本组成。约束条件式(2)意味着某供应点运到各救援中心的物资总量不超过该供应点的总供给能力。式(3)表示各救援中心向某灾区输送的救援物资总量须满足该灾区对物资的需求。式(4)是有关救援中心处物资流量的表达式,含义是各救援中心处的物资输入总量等于物资输出总量。式(5)是各救援中心处对物资流量的容量限制。式(6)是对选择建立救援中心的个数约束。式(7)、(8)分别是对物资分配决策变量的非负限制及指明选址决策变量是0-1变量。
1.3 差异化反应时间指征的获得
参考文献[1,13],有许多因素会影响救援中心j处的应急反应时间,主要包括其所在区域的经济发展水平Ej、自然地理位置Gj、物流发达程度L j、受灾害影响程度Aj、综合交通可达性Rj、基础设施竞争力Oj以及应急政策关注度P j等。本文借鉴这一观点,对上述影响救援区域异质性的各指标因素进行相应的数据搜集,具体操作:在衡量救援中心处经济发展水平时调研该城市GDP、人口数量、居民人均可支配收入和人均消费支出4个方面的数据[14];选用货物周转量来测评物流发达程度[15];以各救援中心到各供应点以及到各灾区的距离来区分各备选点的自然地理位置;综合运用一些可达性计算方法来估测区域交通可达性[16];在对各救援中心受灾害影响程度进行评估时,考虑所在区域距灾区距离、伤亡人数、经济损失和灾害强度4 个方面的因素[17];用城市基础设施竞争力指数来衡量各救援中心区域在基础设施方面的投入[18];在度量应急政策关注度时,选择以政府官方网络新闻客户端等媒体的用户数量表示各区域民众对相关政策的关心程度,这是考虑到在当下电子信息社会,政策信息常通过传统媒体和网络新媒体等方式同时传递,关注某网络新闻媒体的用户数在一定程度上能体现相关政策的关注度[19]。
明确评估体系中各指标因素并经调研获得相关基础数据,按照各因素对应急反应时间的影响作用分为正向(Gj、A j、Rj)和负向指标(Ej、L j、Oj、Pj)[1,13]。由于各指标因素具有不同的单位和差别化的变异程度,为了消除量纲和变量数值变异的影响,可将各正向或负向指标因素分别按照下式进行平移极差变换[14-15]:
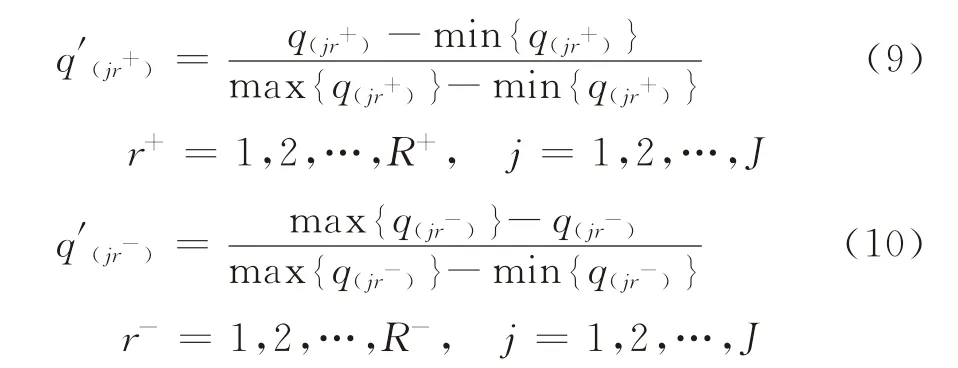
经式(9)、(10)处理的数据仍可能会出现差异化的离散程度,故还需将每一组数据平均化后得如下形式的各救援中心处标准化数据平均值:
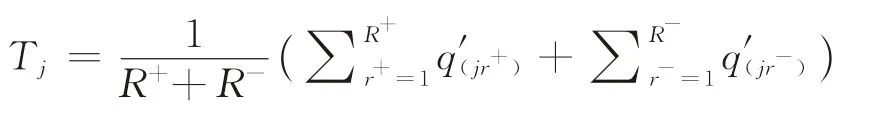
以此作为各救援中心差异化应急反应时间指征的度量。
1.4 各灾区差异化需求的估测
除了表征各备选救援中心差异化的应急反应时间外,应急物资选址-分配优化中还需考虑到各灾区不同的受灾情况。为此,本文选择用各灾区差别化的应急物资需求量来刻画受灾程度的异质性。参考文献[20],各灾区k的应急物资需求与受灾等级λk、幸存人数δk以及幸存者对物资的人均消耗率βk相关,可用如下函数关系表达:

式(11)中,灾区幸存人数可由灾后事故总结报告获知;对某类应急物资的人均消耗率可参照人道主义救援最低标准来估测[21];而对于各灾区受灾等级,可由受灾危险度、受灾强度测度、经济损失以及伤亡人数统计等关键指标加以综合评估[17]。
2 模型求解算法
本文所构建的考虑各救援中心和灾区异质性的选址-分配模型属于典型的混合整数规划,决策问题包括救援中心的选址和上下3层级间的物资分配,模型变量和约束较多,求解复杂性会随着问题规模的增大而快速增加。而应急物资救援活动本身具有强时效性要求,寻优效率较高的智能优化算法因能克服传统精确算法单点搜索效率低的缺点而成为求解此类模型的主要方法。与其他常用的粒子度、模拟退火以及蚁群等智能优化算法相比,遗传算法具有多点并行搜索、不依赖函数的可导性、不易陷入局部最优、速度较快及鲁棒性较强等优点[22-23]。针对所构模型特点综合考虑,本文选择应用遗传算法实施模型求解。
2.1 遗传算法设计
(1)编码选择。决策变量zj包含数值分析与逻辑分析两部分,用二进制编码;x ij和y jk属于数值类型,若采用二进制编码,会出现问题规模变大时算法搜索空间增加幅度较大的现象,故在此采用浮点数编码方法,如此编码串不会太长且运算效率较高。
设计3个子串:子串1 表示救援中心备选点j是否被选中,1表示被选中,否则为0;子串2表示由供应点i到救援中心j的物资量;子串3表示由救援中心j至灾区k的物资量。
(2)初始化种群。设置一定种群规模,随机产生初始种群。种群大小会影响遗传算法求解结果的全面性和计算效率:种群较小时,运算速度快,但无法保障其多样性;种群较大时,虽满足多样性,但计算量增加、运行效率低。对本文所构模型的求解,随机数易使每次运行结果都不尽相同,然而,当种群个数大于50时,能够使算法在较广搜索范围对最优解的确定更加精准和稳定。
(3)设计适应度函数:
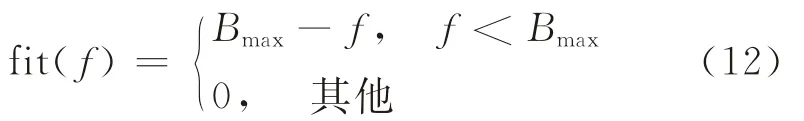
因为本文模型是求解最小值问题,所以取一个相对较大数Bmax,作为目标函数f的最大估计值。设置如式(12)的适应度函数,以保障群体中较好的个体具有较高的适应度值。
(4)选择操作:
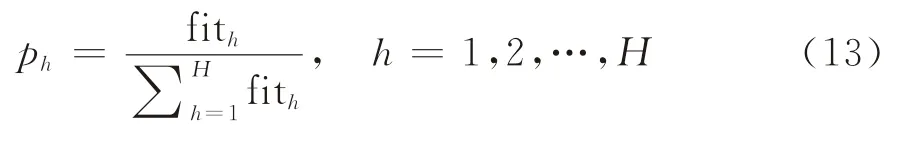
选择是从群体中挑选优质个体组成新群体的过程,其目的是为避免丢失遗传信息的同时提高全局收敛性。在此采用轮盘赌选择策略复制个体进入下一代。p h是第h个个体被选中的概率,fith是第h个个体的适应度。式(13)意味着对个体的选择概率与其适应度值成正比。
(5)交叉和变异操作。在将原有优良基因遗传给下一代的同时,为产生更加复杂的基因结构个体、保证种群多样性,提高算法的全局搜索能力,对决策变量zj进行交叉操作。考虑到操作简单及计算量小的优点,本文选择单点交叉方式[22-23]。为防止出现误码和信息丢失现象,且为增强算法局部寻优能力和有效性,也对zj=1时所对应的决策变量x ij和y jk进行变异操作,在此选择非均匀变异。相较其他变异方法,非均匀变异方式更侧重于搜索父代附近的微小区域,且能使个体在搜索空间内自由移动[22-23]。不同的交叉、变异算子会显著影响算法的收敛速度,故求解时需综合考虑给予合理取值。
(6)算法终止条件。设定算法终止的最大迭代次数maxgen。当迭代次数gen>maxgen时,算法结束,此时将进化过程中出现的具有最大适应度的个体作为模型最优解。
2.2 求解算法步骤
(1)初始化,随机生成若干选址-分配决策方案的个体,设置迭代计数器gen=0,设置最大迭代次数maxgen;
(2)将模型中的目标函数转化为适应度函数fit[f(x)];
(3)对每个个体进行解码,得到选址-分配方案和各个体的适应度值;
(4)判断(3)中适应度值最大的个体是否满足约束条件限制,若满足则转(7),若不满足则转(5);
(5)根据轮盘赌选择法对个体进行选择,并采用单点交叉和非均匀变异对个体进行交叉、变异操作,产生新一代个体;
(6)令gen=gen+1,转(3);
(7)判断是否满足终止条件,当gen>maxgen时,算法终止;
(8)输出最优结果。
3 案例分析与参数仿真
下面以2008年汶川地震为讨论案例,依托所建指标体系采集真实数据再结合相关参数设置,将遗传算法应用于所构模型求解,并将最优解与未考虑区域异质的应急物资选址-分配方案进行对比,结合对关键参数实施敏感性分析,以验证模型和算法的可行性和有效性。
3.1 案例相关数据采集
从多个极重或较重受灾区域中选择汶川县、北川县、绵竹市、青川县、都江堰市、广元市朝天区(K=6)作为需要接受应急物资救助的灾区需求点,2个应急物资供应点(I=2)选定为南京和广州,灾区附近可供选择构建临时救援中心的5个备选点(J=5)分别为:重庆、成都、昆明、贵阳和兰州。考虑救援时效性和成本等原因,假定从5 个备选点中至多选择3个建立临时救援中心实施物资的集散,即M=3。本案例中仅关注震后各灾区对瓶装矿泉水这类应急物资的紧急需求。由Baumol-Wolfe模型经验值将救援中心处流量指数θ设为1/2[12]。为体现应急救援中时间紧迫性要求,将救援中心处单位反应时间-损失成本转换系数α设为较大取值500 000。
对2008年5个备选救援中心处应急反应时间相关的指标数据实施网络调研。对这些基础数据进行如1.3节所述的去量纲标准化处理,最终计算出衡量各备选救援中心应对灾害反应时间快慢的T j值,分别为:重庆(0.24)、成都(0.37)、昆明(0.64)、贵阳(0.57)和兰州(0.72)。参考震后评估报告和相关统计年鉴,分别搜集6个灾区在受灾面积、受灾人口和受灾强度等方面的原始指标数据,以此评估出各灾区受灾等级,如表1所示。表1还给出了各灾区的幸存人数和人均水资源消耗量[21],以及由式(11)测算出的各灾区对应急物资差别化的需求量。
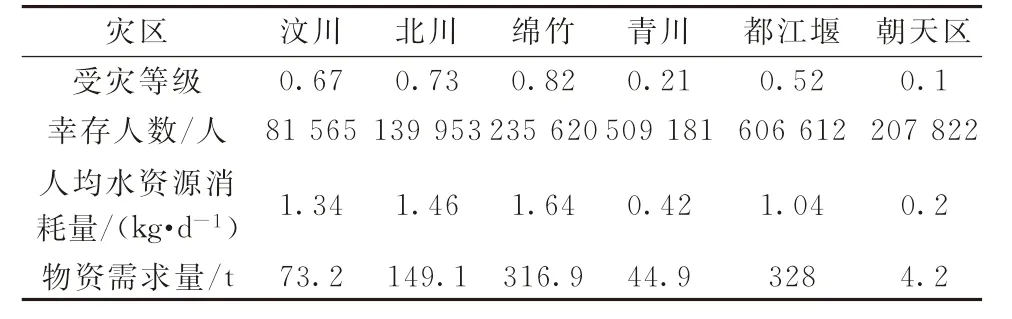
表1 各灾区应急物资需求估测所需的相关指标数据
另调研两供应点到5个备选救援中心、以及5个备选救援中心到6个灾区的单位应急物资运输成本,如表2所示。表2中还列出5个备选救援中心的容量约束、被选为构建救援中心的固定成本和各备选救援中心处对单位应急物资的处理成本。此外,两供应点处对瓶装矿泉水的物资供应限制均设置为1 000 t。

表2 相关成本和容量约束数据
3.2 求解结果比较
算法相关参数设置:种群个数为200、交叉算子为0.65、变异算子为0.35、最大迭代次数为2 000。在MATLAB R2015a中实现用来求解模型的遗传算法,在汶川地震案例背景下以救援中心差别化应急反应时间和灾区受灾差异为例,得出面向区域异质性的应急物资选址-分配优化方案:救援中心最佳选择建立在重庆和成都市,并将供应点到两个救援中心、以及这两救援中心到5个灾区的应急物资最优分配量如表3所示。此外,为比较分析,也对相同案例场景下不考虑区域异质性的应急物资救援方案进行求解(见表3),即决策目标不考虑对差异化应急反应时间损失成本的考量、且约束条件对6个灾区的受灾情况也不做区分(受灾等级均设为0.4、人均水资源消耗量统一取值为0.8 kg/d)。为避免最优方案的偶然性,本文将考虑和不考虑区域异质性的选址-分配决策模型分别进行20次的运行求解,发现两种情形下最优解比较均展现如表3中的类似规律。

表3 考虑与不考虑区域异质性的应急物资选址-分配最优方案比较
首先,观察表3中两种情形下最优选址方案的比较,发现考虑区域异质性时选中的正是应急反应时间较快的两个救援中心备选点,故从救援时效性角度来看,考虑区域异质性的选址方案更加合理;然后,经对比发现,表3中两种情形下应急物资的最优分配也存在较大差别。考虑区域异质性时两救援中心从供应点获得物资的总量更具差异化(表现为标准差较大,492.1>15.4),且6个灾区从救援中心获得物资总量的差异性也更加明显(127.5>27.2)。这恰好说明,若将区域异质性纳入应急决策考量中,会使得应急方案更关注救灾和受灾的差异性,以致应急物资的集散分配更具针对性和有效性;最后,比较表3中两种情形下应急方案所致的运营成本和时间损失成本,其中运营成本包含运输成本、救援中心处固定构建成本及物资处理成本。发现考虑区域异质性的应急物资救援方案显然更优,不仅因选择反应时间较快的两个救援中心而使时间损失成本较低(3.05×105<4.70×105),而且运营成本相较不考虑区域异质性的情形也耗费更低(34 610<37 256)。其主要原因在于同为已满足物资需求的情景,不考虑区域异质性时的物资分配会出现浪费的现象,故易导致其运营成本更高。
上述比较分析说明,若将真实存在的区域异质性这一现象考虑进应急优化中,能使决策方案的现实指导意义加强,从而更好地在实际救援过程中被贯彻执行、更大程度地发挥应急效用。
3.3 参数分析
(1)区域异质性因素的影响。模型关注的区域异质性因素反映在两方面:体现救援中心异质性的反应时间指征Tj和刻画灾区异质性的物资需求Dk。由于后者是相对客观因素,故在此仅探讨救援中心反应时间指标因素的变化对救援方案的影响,以救援中心备选点重庆为例,图1所示为对应急物资分配总量和应急总成本的影响。其中有关应急反应时间影响因素,本文选择观察物流发达程度(以货物周转量度量)和应急政策关注度(以政府官方微博粉丝数衡量)的变化。

图1 区域异质性因素对物资分配总量和应急总成本的影响
结果显示,货运周转量与政府官方微博粉丝数的变化虽然均未引起救援中心最优选址方案的改变,但由图1(a)、(b)可以看出,货运周转量的减小使应急救援物资分配总量和应急总成本呈现增大趋势;而随着政府官方微博粉丝数的增加,物资分配总量和应急总成本均越来越小。这是因为救援中心所在城市货运周转量的减小意味着该区域物流发达程度减弱,一定程度上导致应急反应时间增大,响应的不及时易造成救援物资在满足需求后的浪费更加严重;而粉丝数的增大某种意义上反映应急相关政策关注度的提升,易使面对灾害的反应时间缩短、应急响应更及时,能有效减缓救援物资的过度调配,从而提高应急救援行动的准确性。
此外,也观察直接改变应急反应时间指征对应急救援决策的影响,仍以备选点重庆为例,发现随着重庆应急反应时间指征的增大,最优选址方案将不再选择重庆作为救援中心;而应急物资的分配同样因更迟缓的响应易出现过度救援的现象,继而引发愈发高额的应急总成本(见图1(c))。
因此,在真实应急管理活动中,需提倡在常态下综合改善影响应急反应时间的各指标因素,例如从提高政策关注度的角度,鼓励应急管理者积极采取与媒体沟通、社会动员等措施,从而有效发挥新闻网络媒体等传播媒介的力量,加快灾害应对相关信息的对外传播,唤起社会各方面对应急救援活动的协作与支持,以实现更高效和准确的应急救援。
(2)单位反应时间-损失成本转换系数α的影响。α刻画应急救援活动的急迫性,该参数的值越大,意味着在救援中心处单位应急反应时间中所造成的人员伤亡和财产损失(用成本来计量)越严重。其他参数不变,将α在(500 000,50 000,5 000,500,50)中改变取值,观察α变化对应急救援决策的影响,不同α情形下应急选址、最优物资分配量以及相关成本的变化如表4所示。
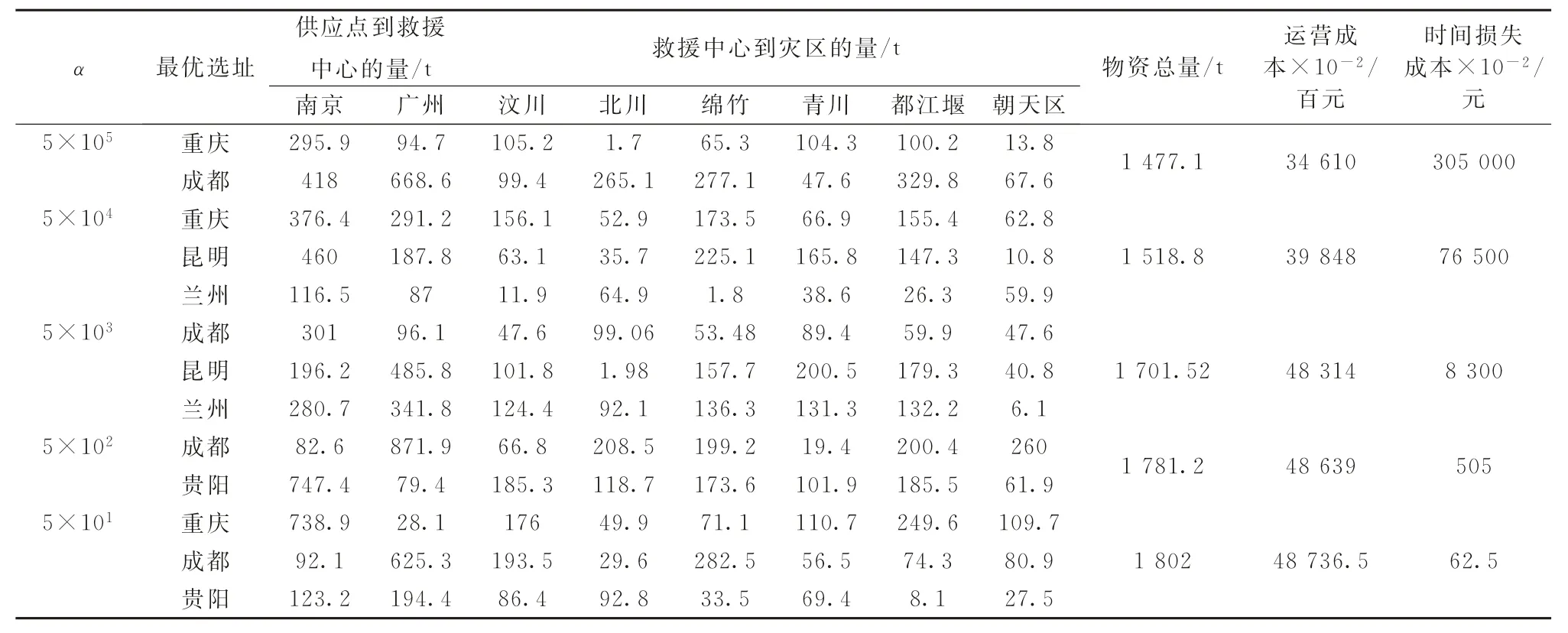
表4 α 变化对应急选址-分配决策的影响
由表4可以看出:
(1)改变α会使最佳选址方案出现明显变化。总体来看,随着α从50逐渐增大到500 000,最优选址方案越来越向应急反应时间短的救援中心备选点(重庆、成都)集中。这符合实际应急需求,即随着救援时效性要求的提高,救援中心选址更倾向于应急响应快的备选点。
(2)观察相关成本的变化。随着α的减小,一方面,救援急迫性变弱,逐渐类似于常规物资调配,时间成本自然呈下降趋势;另一方面,运营成本却呈增大趋势,究其原因发现很大程度上仍是因为在已满足需求的前提下物资分配总量仍在不断增大。这实际上再次演绎了救援响应临近结束时常常出现的应急物资浪费的现实局面,从侧面强调了为减缓过度救援现象,紧急状态比常态物资调配情形更亟需考虑区域的异质性,也间接表明在应急物资选址-分配方案优化中考虑区域异质性特征能够增强决策的准确性和有效性。
4 结 语
救援物资的选址-分配是灾前准备或灾后响应的重要任务,关系到整个应急管理活动的成效。以往应急物资选址-分配研究中,大多忽略救援网络中各节点区域(供应点、救援中心和灾区)的异质性特征。本文创新性地构造“差别化的应急反应时间”这一指征来刻画备选救援中心异质性特征,且将其纳入选址-分配决策的优化目标中考量,并结合各灾区受灾差异,构建了一个面向区域异质性的应急物资选址-分配模型。通过遗传算法对模型进行求解,并与未考虑区域异质性的选址-分配决策方案对比。最后,以2008年汶川地震作为案例背景实施关键参数的仿真分析,全面论证所构模型和算法的可行性和有效性。模型求解和参数分析结果为政府部门在面对突发灾害时制定科学高效的应急管理方案提供有益参考。
未来研究可尝试突破单种物资单次分配的前提假定,考虑实际应急救援中常出现的多种类物资多周期分配的场景;可进一步针对性构建更符合特定应急场景的综合评价体系,以实施对差别化应急反应时间和受灾差异的更合理有效度量;另外,所构模型未考虑各供应点或各救援中心间物资的相互救助,今后也可深入探讨多个救助供应点甚至各灾区之间救援物资相互协调应急的作用。

