基于过程的雪盖模型研发II——应用

高 洁

(水电水利规划设计总院，北京100120)

积雪是冰冻圈对气候变化最敏感的因素之一[1]；同时，积雪对气候变化的响应又进一步影响整个水文循环过程。因此，模拟和预测雪盖厚度、密度等变化是了解水文循环过程对气候变化响应的重要环节。

各种基于温度指标或能量平衡的融雪模型被广泛应用于雪盖对气候变化的响应分析。Lazar和Williams首先通过RCM MM5和GCM降尺度方法预测Colorado，Pitkin，Aspen山区(海拔2 422～3 418 m)2030年和2100年气温、降水等变化趋势。在中度温室气体排放的情景下，相对于1990年的气温水平，2030年升温幅度1.8～2.5℃，平均升温2℃；2100年升温幅度4～6℃，平均升温4.8℃；基于温度指标的Snowmelt Runoff Model(SRM)[2- 3]被用于预测融雪洪水发生时间，基于过程的一维能量平衡模型SNTHERM[4]被用于预测积雪密度变化。结果显示，中度温室气体排放条件下，2030年山顶积雪融化提前25～27 d，2100年山顶积雪融化提前31～37 d，2030年表层雪盖密度增加近20%[5]。Rasmus等[6]采用考虑雪层微观结构的一维能量平衡积雪模型SNOWPACK[7]结合RCM RCAO设置情景，对比分析芬兰1980年～1989年和2080年～2089年积雪特征的变化。发现3月15日同期，芬兰的5个观测点中Santala积雪密度降低23 kg/m3，其余4个观测点均出现密度增大的现象，平均增大33 kg/m3。雪温普遍升高，融雪期提前13～19 d，最大雪水当量(SWE)降低至1980年～1989年均值80%。Ma和Cheng[8]将SRM应用于西天山Gongnaisi River流域，在气温增加4°C的情景设置下，4、5、6月融雪径流分别增加68.1%、44.2%和9.1%；7、8、9月融雪径流平均减少27.7%、49.4%和56.7%。

本研究采用基于过程的能量平衡雪盖模型Snow Column Model[9]，模型驱动数据来源于美国Niwot Ridge Long-Term Ecological Research Site项目(http://culter.colorado.edu/NWT/)。以洛基山脉东侧的Niwot Ridge实验场为研究对象，通过1997年～1999年4月～6月006号雪坑详细观测资料进行验证。在1996年～1999年实测数据基础上设置气候变化情景，分析雪深、密度、雪水当量对不同情景的响应。

1 研究区域概况

研究区域Niwot Ridge位于美国科罗拉多山脉东侧(40°03’N，105°35’W)海拔3 517 m。该区域内树线海拔约3 350 m(http://culter.colorado.edu/Subnivean/Subniv_site_desc.html)。平均每年冬季积雪深度在2 m以上，最深时超过8 m；平均年温差21℃，日温差达6～8℃[10]。

Subnivean观测场位于树线以上大约150 m相对平坦的鞍状山脊，辐射资料经由仪器直接观测，湍流通量采用空气动力学法(aerodynamic profile method)计算获取[11]。数据分为4个等级：level 0是仪器直接记录的以10分钟为间隔的原始数据；level1是经过插补和过滤后的数据；level2是在level1的基础上进行平滑和平均的小时/日数据；level3是经过严密分析和纠错后的数据，当时仅处理了1994和1995两年。其他可下载的level1和level2数据长度为1996年～2008年。相应仪器说明：①短波辐射和反射，采用Kipp & Zonen CM14辐射计和反照率测量仪；②大气辐射和地面发射长波辐射，采用Kipp & Zonen CG2长波辐射计；③气温和相对湿度，采用Vaisala HMP35C温度/相对湿度探头；④风速和风向，采用R.M.Young风速风向仪传感器05103，位于雪面高度0.5 m、1.0 m和2.0 m，level2仅使用2.0 m相应数据；⑤雪深，采用Campbell Scientific UDG01超声深度探测器，置于地面高度6.0 m。Niwot Ridge/Green Lakes Valley snow cover profiles数据集是雪盖剖面每隔10 cm取样1000 mL观测密度。其中，006测点在subnivean气象观测站北侧30 m。

本文使用数据：①Subnivean level2小时观测数据(1996年～1999年)；②006号雪坑的雪盖剖面数据(1996年～1999年)。

在1996年4月25日～6月21日模型率定[9]的基础上，进一步以1997年5月7日～5月30日，1998年4月28日～6月22日，1999年5月18日～6月22日验证模型，采用计算步长1 h。

经验证，模拟结果与实测数据基本一致(见图1)。其中，1997年5月30日的雪深结果表明，计算值比实测值明显偏小，但是密度、雪温计算成果与实测数据一致。鉴于1997年计算时段略短，只包含4个雪坑观测记录，误差较大测次的代表性不足以保证。1999年6月22日雪深计算值比实测偏厚，密度计算值比实测值偏大，这极可能与实际发生了风吹雪现象有关。1998年实测积雪密度波动较大，存在观测有误的可能性，但计算结果可基本保持在实测波动范围内。

2 模型应用

2.1 情景设置

根据1996年至1999年观测数据的起讫时间，选取4年中观测资料全程覆盖的时段：5月18日至5月30日，共312 h。计算每小时4组(每年为一组)数据在短波辐射、长波辐射、气温、感热和潜热通量上的均值E和标准差σ，以E，E+σ，E-σ作为不同的边界条件，计算雪盖变量对不同情景的响应。本文对较为敏感的入射短波辐射、反射短波辐射和潜热通量进行E±σ变动，长波辐射和感热通量采用4年相应时段的均值E作为输入条件。

在模拟期312 h内，气温E的均值2.3℃，气温变化标准差σ的均值3.1℃。本研究设置情景是在气温平均变化2σ(6.2℃)的变幅内，分析雪层厚度、密度和雪水当量的响应情况(见表1)。

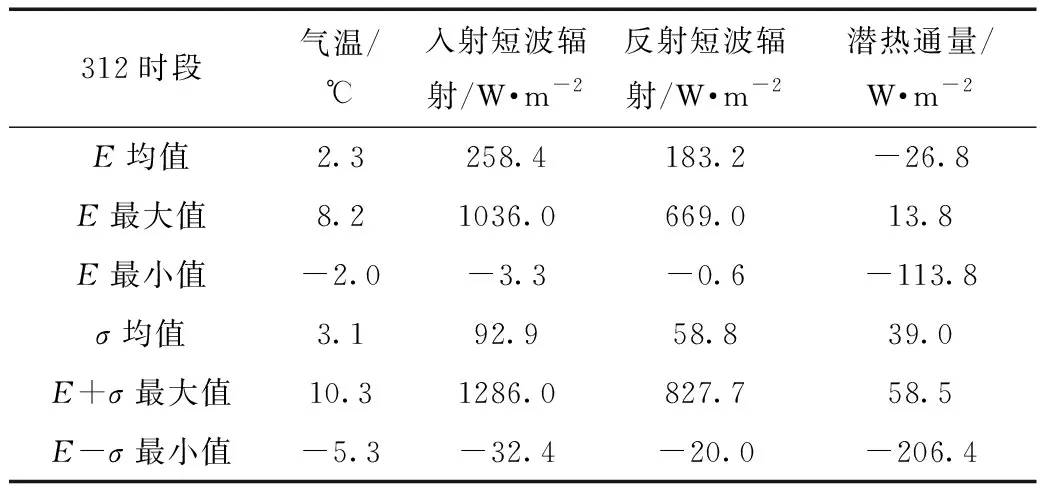
表1 情景设置的变化范围

2.2 影响分析

(1)随着入射短波辐射增加、反射辐射减少、潜热通量(从大气到雪层)增加，雪盖消融，雪水当量减少。

(2)在本例中，雪水当量采用雪深(m)×密度(kg/m3)的方式来表示。模拟中，雪水当量的减少体现为雪盖变薄，密度增加，但两者乘积减少。

(3)随着雪盖输入能量的增加，雪水当量减幅增大、雪深降幅增大，但是雪盖密度的变幅较为复杂。

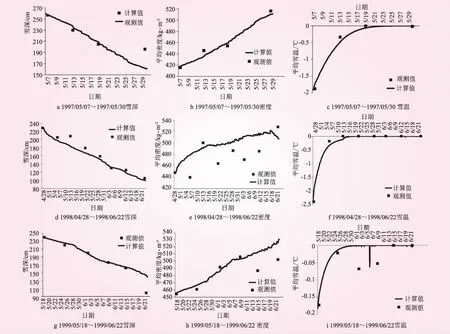
图1 雪深、密度、雪温实测数据与计算值对比

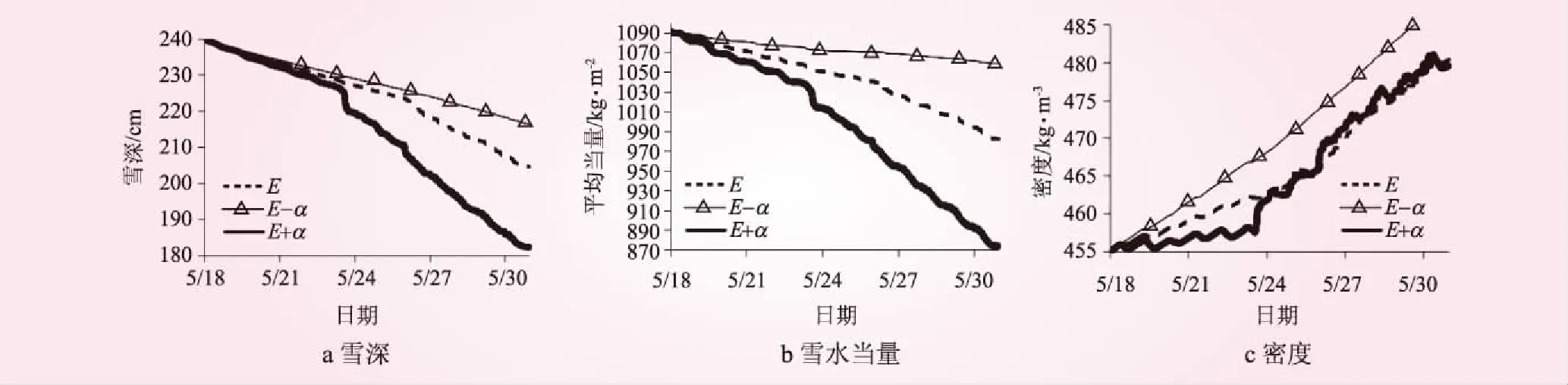
图2 短波辐射变化的影响分析

(4)随短波辐射增加，在模拟期前期(05/18～05/25)，密度增幅较小；在模拟期后期(05/25～05/30)，变化幅度变大。反射短波辐射与入射短波辐射的效果类似，但方向相反(见图2和图3)。

(5)雪盖吸收能量后，一方面体现为雪层整体消融、厚度变薄、融雪出流；另一方面是雪层部分消融、上负雪层荷载压实、本层密度增加。消融初期，入射能量较大的情况下，整层消融作用主导，雪盖厚度减小效果显著；入射能量略小，则雪盖以部分消融压实、密度增加效果显著；到了消融后期，随着辐射增加，雪厚加速减小且密度加速增大。

(6)潜热通量的效应(图4)与短波辐射原理相同。从雪层传输到大气的潜热通量少，则雪层内的能量(E-σ)多。反之，E+σ对应于进入雪层中的能量较少。因此，消融前期，潜热通量E-σ情景时，雪盖内能量多，雪层整体消融，对应于厚度变薄的效果显著；E+σ时雪盖内能量略少，雪层部分消融，密度增加的效果显著。在消融后期，雪盖中累积能量足够大，厚度减小和密度增加的效果并存。但是鉴于潜热计算的情景中σ=39.0 W/m2，小于短波入射和反射的情景变幅σ(92.9 W/m2和58.8 W/m2)。因此，从消融前期到后期的转折较晚，在5月28日～5月29日之间。

图3 短波辐射反射变化的影响分析

图4 潜热通量变化的影响分析

Snow Column Model运行结果显示，随着进入雪层的能量增多，存在雪层消融、积雪密度增加的现象，与前人的研究成果一致[6]。亦发现，随着能量输入，雪盖密度增幅不是单调变化。

3 结 论

本文采用基于过程的一维能量平衡雪盖模型Snow Column Model，通过气候变化情景设置，研究Niwot Ridge， Colorado，Front Range of Rocky Mountains 006号雪坑的雪盖变化。基于1997年～1999年结果验证，通过1996年～1999年消融期内实测短波辐射、长波辐射、气温、感热和潜热通量数据，分析这4年消融期内312 h数据在相应时刻的均值和标准差，作为情景设置的基础。考虑气温变幅6.2℃的条件下，不同的入射短波辐射、反射短波辐射和潜热通量边界条件，分析雪盖密度、厚度和雪水当量的响应情况。随着消融过程的发展，雪盖厚度减小、密度变大、雪水当量减少；在改变辐射通量的情景下，随着入射能量的增大，密度增幅存在先减小后增大的过程。