儿童火灾逃生教育系统交互路径研究
黄天昊 , 姚 君
(1.中国矿业大学 建筑与设计学院,江苏 徐州 221116;2.徐州市工业与智能装备创新设计工程技术研究中心,江苏 徐州 221116)
0 引言
根据近年来的我国火灾伤亡数据统计,平均每年都有近千名儿童死于火灾[1]。当前对儿童的火灾逃生教育仍然局限于单调、单向的视频和图像形式,合理的逃生意识无法深入儿童。因此亟需一种更适合儿童的方式进行火灾模拟演练,使儿童掌握应急的逃生知识和技巧。采用虚拟现实技术进行灾害模拟具有逼真、安全、成本低廉、易于重复等多种优点[2]。通过虚拟现实设备,儿童可以实现身处火灾场景的真实感受,能够很好地实现儿童紧张、慌乱的真实心理。在这样的“真实”、“安全”的火灾现场进行一次次火灾逃生模拟,既没有实地演习操作的复杂性,同时在逃生中还能真实地反映逃生人员的行为特征。蚁群算法所体现的个体之间的独立和联系,以及合成统一系统的整体性[3]正满足以上逃生人员的行为特点。本研究基于以上背景探索现有条件下虚拟现实技术和蚁群算法在火灾逃生教育交互系统中的应用,探讨基于蚁群算法的虚拟现实技术在儿童火灾逃生教育系统中的交互路径问题。
1 VR技术和蚁群算法的介绍及应用
1.1 虚拟现实交互技术
虚拟现实交互技术是一门新兴的综合信息技术,它通过计算机图形学构成三维数字模型,产生逼真的虚拟环境,在视觉上给用户一种立体的虚拟环境。与通常的计算机辅助设计系统所产生的三维模型不同,它不是一个静态的世界,而是一个互动的环境。虚拟现实交互技术能够现实彻底地、立体地虚拟化,人们将身在虚拟环境中感受周围的事物。
随着虚拟现实交互技术的不断发展,应用方面也越来越广,尤其在各类逃生教育系统中的应用。Sharma S等[4]用虚拟现实交互技术建立了地铁站的模拟逃生系统,通过计算机模拟和逃生人员的控制完成地铁逃生演习。孟凡兴等通过环绕式视觉效果及特殊的虚拟现实设备,以达到模拟真实的火场效果[5]。Kinateder M等[6]通过虚拟现实技术分析各种火灾逃生情况,展现出虚拟现实技术在逃生教育系统上宽广的应用前景。张磊等[7]人利用VR技术建立了高铁站模型,针对火场中火势蔓延的研究和对测试人员的问卷调查,综合分析提出了有限细胞法。
1.2 蚁群算法介绍
人员在逃生过程中的移动特性和自然界中的集群演化过程十分类似。相对于传统的最优路径算法来说,演化算法更契合此类问题的解决。因为研究发现其具有良好的启发机制,能够适应人员逃生时复杂灵活的路径选择特性,并且速度快,容易收敛求得最优解。
1991年意大利米兰学院Dorigo等[8,9]人提出蚁群算法(Ant System),用于求解TSP等组合优化问题。蚁群在搜索食物的过程中,个体之间的交流及正反馈是通过分泌的信息素实现的。这种特征与火灾逃生人群的行为十分相似,所以基于蚁群算法实现虚拟现实逃生模拟及交互路径选择时非常合适的。
本文构建的儿童火灾逃生教育系统中虚拟交互技术能够生成逼真的视、听、触觉一体化的特定火灾场景。儿童借助必要的设备实现人机交互,模拟在火场中的真实环境的感受和体验。虚拟逃生教育系统会结合该场景下的各种情况,最终选择一条最优逃生路径交互给儿童,按照指引的交互路径逃生,从而减少伤亡。
2 火灾逃生教育系统构建及交互路径选择
本文主要研究构建的逃生教育系统中的交互路径的选择。交互路径定义为一种针对特定火灾场景实时的最优逃生路径。火场中的火势蔓延过程是十分复杂的,需要根据每个火灾场景来结合分析。所以火灾逃生教育系统中虚拟现实交互技术进行模拟的不仅仅只是一个静态的火灾场景,而是要具体分析各种影响因素的动态过程,所以交互路径也会根据蚁群算法实时更新。尤其在火灾场景需要分析具体的建筑结构分布、烟雾扩散规律、逃生人员心理变化等,从而模拟出一个更真实有效的动态火灾发展和逃生过程,其中交互路径也是一种动态最优化的结果。
2.1 构建逃生教育系统的结构模型
用点阵图构建建筑俯视的二维结构图,再利用蚁群算法实现儿童逃生交互路径的选择。其中二维点阵图表示建筑结构的细节精度和点阵的维度成正比。逃生教育系统会根据火情,在构建的栅格图中得出可以疏散的实时交互路径。点阵图一般采用以下两种方法直观地表示:
(1)坐标系法:把点阵左下角的那个点作为坐标原点(0,0),同直角坐标系X轴水平向右为正方向,Y轴竖直向上为正方向,点阵中的任一点都可以通过具体坐标(x,y)唯一表示。
(2)标序法:以从左到右,从上往下的规律对点阵图上的点进行标序,给每个点一个唯一的序号n,点阵左上角第一个点记为1开始。
点阵的定义规则:①建筑内部的房间区域为静态障碍区域,表示路径无法通过房间周围的墙壁;②建筑内部的支柱等结构也定义为静态障碍点,无法跨区域通过,只能绕行;③若某个点四周都无障碍节点,则逃生人员在该点可以向四周相邻四个方向的点移动;④其中安全逃生出口和逃生人员起始位置在点阵图中都以特殊颜色把这些点标识出来。
2.2 逃生教育系统对交互路径选择的影响因子
本文中蚁群算法涉及到的参数有:信息启发式因子α≥0,表示对路径记忆的重要程度、期望启发式因子β≥0,表示某启发信息对路径选择的影响程度大小、信息素挥发因子0≤ρ<1,表示路径记忆停留的消逝程度(同样的1-ρ代表信息素残留因子),以上都会随时间变化、蚂蚁数量m以及信息素强度Q,表示全局的信息量大小,每次交互路径选择完都会对Q值进行更新,从而保证得到实时的交互路径。
蚁群算法构建的是一种动态的交互路径选择模型[10],会根据不同的动态环境变化,不同的起始位置和不同的起火点,通过通道节点来选择最优的通道路径,即逃生时间和距离综合考虑最短的路径。逃生教育系统中的蚁群算法对动态交互路径的选择规则如下:
(1)每次分别根据相邻节点来选择路径。
(2)以最快达到出口为目的,当路径到达出口时便停止算法。
(3)每条路径都是从起始点开始,连接若干个每个通道节点,最终寻找到一条最优路线。
(4)后续要加入考虑起火点火势、烟雾、能见度等动态因素对路径的选择更合理,优化算法,而不仅仅考虑的是几何长度。
2.3 逃生教育系统对动态交互路径的选择流程
通过对建筑内部具体的结构分析,构建相应的二维点阵图,分别标识出来建筑中的房间等障碍节点、通道和门等可通行节点。再根据虚拟逃生教育系统所模拟的火灾场景,赋予每个节点的静态和动态参数。进行蚁群算法的不断迭代,在不断更新的火灾场景参数下,根据交互路径选择策略等约束条件下,计算最终逃生到达安全出口的路径当量长度,从而输出交互路径。
3 逃生教育系统中蚁群算法的建立
本文主要采用蚁群算法进行火灾现场逃生路径的模拟。该算法考虑了建筑中火灾发生时影响儿童逃生时间的各种因素,将这种火灾现场的影响因子转化为算法中的动态参数,引入建模当中。采用蚁群算法优化了交互路径的选择策略和动态因子的更新策略,能够大大提高对路径搜索的最优化及搜索效率。能够在每一次搜索路径之后,根据火源和人员情况,不断更新动态因素,从而提高了算法的收敛性。
另外本文以点阵的形式表示建筑的内部结构,可以自由地重绘点阵数据来描绘建筑中各种通道和障碍物的分布,也可通过变化维度来改变空间的大小和一些细节特征,构建一些更为复杂的建筑结构。本文采用40*40的点阵图来描绘建筑中某层的平面结构图。
采用MATLAB进行编写算法,在模型建立的过程中,首先利用点阵图的形式建立矩阵,代表建筑结构。平面结构图的细致程度和点阵的维度成正比,但是维度过大,建筑细节过于精确,会占用大量的计算机空间,使算法模拟的搜索路径数按指数增长。同时过小的维度,会导致模拟的建筑平面结构过于粗糙。如图1是采用顺序定位法建立的点阵。
在点阵图中,如果某个点的位置周围没有障碍物,都是可移动区域,那么人员的逃生方向可以分为四个方向,如图1所示。

图1 点阵模型建立Fig.1 Lattice model establishment
建立点阵模型之后,还要对应建立起内部详细的结构模型,能够将其内部通道的逻辑对应到图中点的可移动方向上,举个简单的4*4点阵结构图为例,如图2所示。图中矩阵中的点即代表了通道中的节点,用Vi(i=1,2,…,15)来表示。其中V0代表人员的初始位置,V11代表了逃生出口的位置,V2、V3、V9、V14代表建筑中的障碍物,剩余白色的点都代表可移动的通道路径。图中已经用箭头标出了点之间的可移动方向,我们可以根据点的表述方式和结构分布之间建立起一种逻辑对应关系 G=(V,E)中。
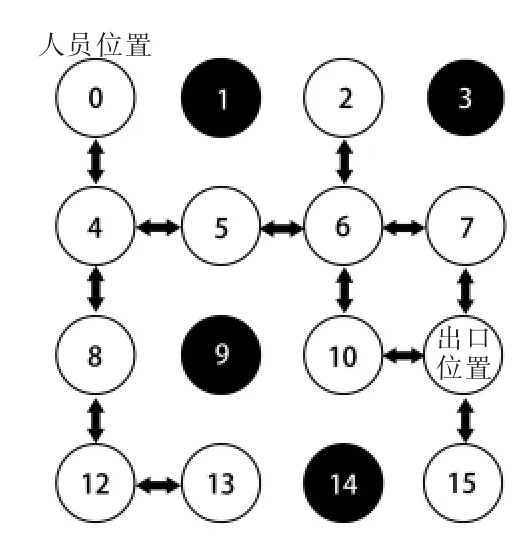
图2 点阵与建筑结构布局逻辑关系Fig.2 Logic relationship between lattice and architectural structure layout
V为图中点阵的集合:

E为图中路线的集合:
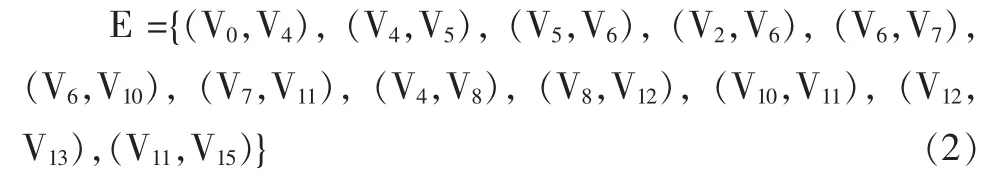
将建筑的每层平面结构转化为由点集V和路线集E组成的 G=(V,E) 逻辑结构图。 其中 V={V1,V2, …,Vn-1,Vn},是由n个点构成的点阵集合,其中的点可分为三种类型:自由移动点、障碍点、火源点。

点阵结构图中,“1”代表障碍点,即不可通过的位置,表示现实中的墙体或者其他建筑阻挡物,这里可以假定与其相邻点之间的当量距离为无穷大,也就代表无法通过。自由移动点顾名思义就是能够通过的路径;同样的,火源点代表起火的位置,或者说火势已经蔓延到的位置。点的类型不是固定不变的,它会随着火灾的变化和火势蔓延情况而改变,自由移动点可能变为阻碍或者火源点。
逃生路径的集合为 E={E12,…,Eij…,Emn},其中路径Eij代表从点Vi到点Vj的矢量性逃生路径,点与点之间能够形成移动路线的条件是当且仅当该相邻两个点之间能够相互连通[11]。
本文以τij代表信息素的浓度,那么在初始阶段各个逃生路径上的信息素浓度都相同,即τij(0)=C,C是常数。假设τij(t)代表t时刻逃生路线 Eij上的信息素浓度,逃生人员在逃生过程中,会根据每条逃生路线上的信息素浓度 τij(t)和启发信息 ηij(t),再采用算法的自适应伪随机比例来寻址确定逃生方向,即逃生人员从点i到点j的概率。

公式中 max{τisα(t)ηβ(t)}代表在与点 i可互相移动的逃生路径集合中,所含信息素浓度最大的点,其中α和β分别表示信息启发因子和期望启发因子。另外ρ0表示逃生人员对信息素察觉的阈值点,ρ0∈(0,1),ρ0值表示了在同等信息素浓度下的初始状态,逃生人员对路径选择的随机性。式子中r是0到1中的等概率随机数,当r≥ρ0时,人员会按照 max{τisα(t)ηβ(t)}来选择信息素浓度最大的路线,反之当r<ρ0时,人员会根据伪随机概率选择路线逃生。
4 蚁群算法对交互路径选择实验分析
由于计算条件限制,采用40×40的点阵图构建平面结构图。首先初始化算法参数,定义O点为人员逃生的起始位置,A、B、C为三个逃生出口,星号点为火灾起火位置,如图 3(a)所示。
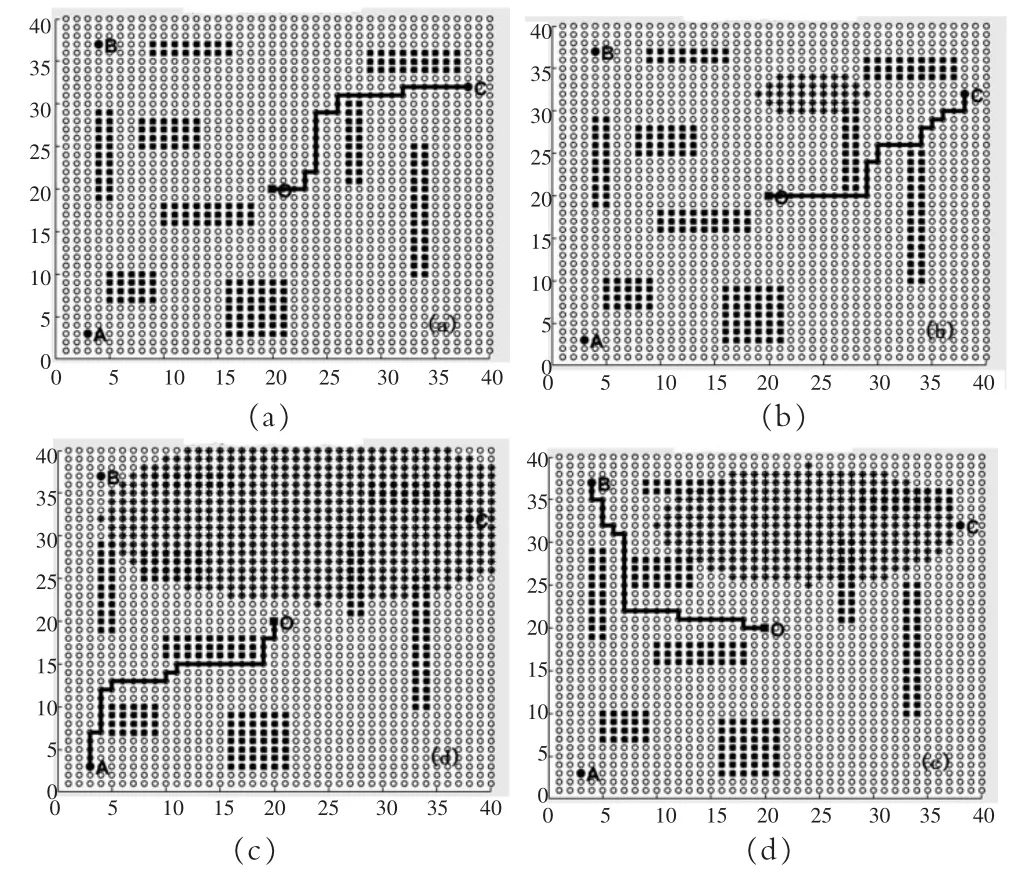
图3 40×40点阵仿真模拟逃生路径Fig.3 40×40 Lattice simulation escape path
经过运算,算法得到图3中曲线为最优逃生的交互路径。随着起火源火势的增长,首先变为图3(b)中的逃生路径,远离开了火灾区域。之后随着火灾的蔓延,C出口已无法逃生,算法自动模拟选择了B出口为最优路径。同样的,当火灾蔓延到B出口,就会自动算出A出口为最佳逃生出口,图中路线为最佳逃生通道。从中看出该算法还是能够非常合理计算出最优的逃生的交互路径,保证逃生人员能够瞬速逃离火灾现场,减少人员伤亡。
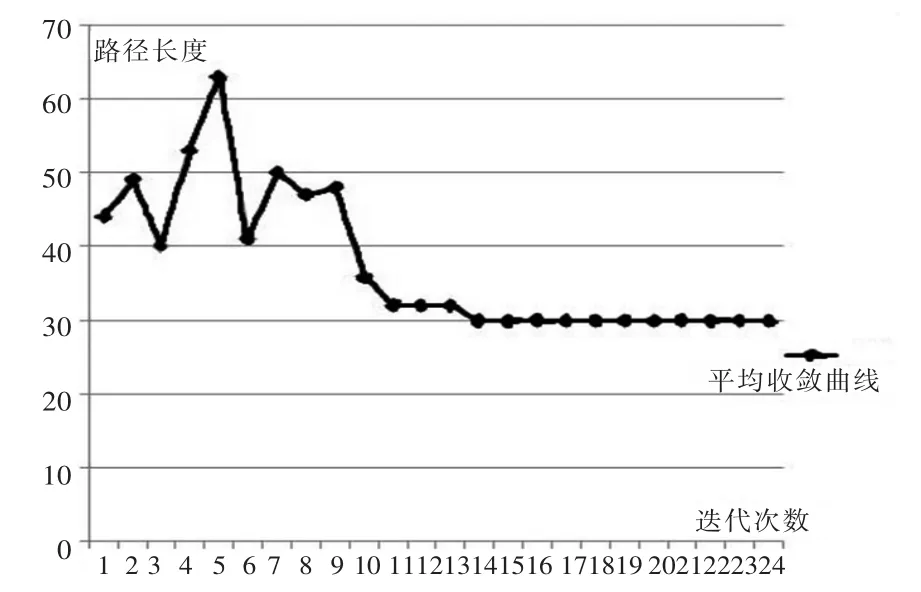
图4 算法的收敛性分析Fig.4 40×40 The convergence analysis of the algorithm
同时我们还对该算法进行了收敛性分析,如图4所示。从图中可以看出,当算法达到第十次迭代之后,求得的最短路径长度就趋于稳定了,达到收敛。说明该算法还是能够较快达到收敛,能够快速地计算出最优的逃生交互路径,也能在不同的火灾场景中,实时更新出相应的逃生交互路径,较好的满足人员能够快速逃生的目的。
5 结论
近年来随着科学技术的发展,虚拟现实技术逐渐渗透到人们的生活中,尤其是在火灾逃生教育系统方面拥有宽广的应用前景。同时由于其具备模拟环境真实、逃生演练安全、低成本等优点,在将来可以全面用于儿童逃生教育当中,不仅能减少儿童的火灾伤亡率,还能提高儿童面对紧急情况的心理素质。
基于蚁群算法的虚拟现实技术能够从火灾本身的自然、物理属性出发,结合儿童疏散特征,利用蚁群算法合理规划最佳设计逃生疏散交互路径。基于虚拟现实和蚁群算法仿真结果,为儿童火灾教育提供相应参考,有利于儿童掌握安全疏散的方法和安全逃生的路径,实现火灾疏散交互路径的动态优化。

