融合K均值聚类和低秩约束的属性选择算法

杨常清

(西安航空学院 材料工程学院, 陕西 西安 710077)

0 引言

高维特征虽然可以准确多样化地表现物体特性，但使用高维数据不仅增大存储空间，还增加运算复杂度。对高维数据进行属性约简，降低数据维度，挖掘数据内部具有代表性的低维属性，已成为机器学习的一个研究热点[1-2]。

属性约简的优点包括能降低处理时间和得到更具有泛化能力和更坚实的学习模型等[3-4]。常见的属性约简方法包含子空间学习和属性选择两种方法。子空间学习是把高维属性从高维空间投影到低维空间，并保持数据间的关联结构，而属性选择是从原始属性集中选择最能代表整个属性集的属性。利用多方向理论，学者们提出了各种属性选择算法。文献[5]将知觉理论赫姆霍兹原理作为特征选择的度量，用于文本分类的特征选择中，取得了较好的效果。文献[6]将类特定变换的新型语义平滑核融入支持向量机模型中, 提出了一种使用语义分类方法来构建高性能的半监督文本分类算法。文献[7] 将皮尔森相关系数(RRPC)的最大相关和最小冗余准则用于半监督学习方法中，利用增量搜索技术来选择最优特征子集，平衡了文本特征提取中冗余特征与计算量间的矛盾。文献[8]提出了一种基于图稀疏的自表达属性选择算法。文献[9]提出了一种基于稀疏学习的低秩属性选择算法，通过嵌入子空间学习方法来调整属性选择结果。文献[10]在经典粗糙集绝对约简增量算法的基础上，提出了一种快速属性选择算法，快速有效地对大规模数据集进行属性选择。文献[11]提出了一种多变量时间序列的无监督属性选择算法，有效解决了大数据集无类别信息问题。文献[12]在卷积神经网络算法中引入无监督特征学习方法，实现了无监督的特征学习方法。文献[13]提出了一种基于蚁群优化的无监督特征选择方法,该方法试图通过几次迭代找到最优特征子集，而不使用任何学习算法，并根据特征之间的相似性来计算特征相关性，从而导致冗余度的最小化。文献[14]从无标注藏文语料中抽取边界熵、邻接变化数、无监督间隔标注等特征，并融入有监督的序列标注藏文分词系统,实现了无监督特征的藏文分词。如何在无监督属性选择中利用类别信息选择属性是当前需要解决的难题。本文借鉴聚类算法、子空间学习和属性选择各自的优点，提出一种有效的属性选择算法。

1 算法描述及推演

1.1 算法描述

本文算法在线性回归的模型框架中有效地嵌入自表达方法,同时利用K均值聚类产生伪类标签最大化类间距以更好地稀疏的结构；其次，在新模型中有效融合低秩约束的属性选择，即利用稀疏学习方法中的l2,p-范数参数p灵活控制结果的稀疏性。

设给定训练集A=[a1,a2,...,an]∈Rn×d，类标签矩阵B∈Rn×k，回归系数矩阵C∈Rd×k，采用线性回归模型如式(1)所示。

(1)

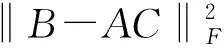
C=(ATA)-1ATB

(2)

任何数据集或多或少都有冗余属性，而颇具代表性的属性往往蕴含数据的空间和类别信息，为了着重凸显数据的独特属性，本文引入低秩来满足实际数据集合中的非满秩需求。线性回归模型可对每类响应变量分别求解，这种求解忽略了响应变量间的相关性，为此，利用低秩约束回归系数矩阵C,如式(3)所示。

rank(C)=r,r≤min(d,k)

(3)

在式(3)上，利用属性自表达方法把A作为响应矩阵，将问题转化为式(4):

(4)

为了使算法获得较好的分类效果，本算法利用K均值聚类将样本聚类到伪类标签中，以最小化类内距离和最大化类间距离。

假定m个类中心，变换后的聚类中心矩阵G=[g1,...,gm]∈Rd×m，利用K均值聚类最小化如下目标函数，如式(5)所示。

(5)

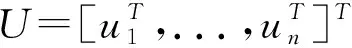
根据bi=aiC，通过回归系数矩阵C的线性转化，可得类内最小间距。把式(5)代入式(4)中可得式(6):

s.t. rank(C)≤min(d,k)

(6)

式(6)回归系数矩阵C∈Rd×k具有低秩约束结构，所以式(6)具有监督分类功能。

lF-范数对噪声和离群数据较为敏感，因此可将lF-范数嵌入到模型中作为正则化项，以此来去除噪声和冗余属性，如式(7)所示。

(aiCi-uiGT)

rank(C)=r≤min(d,k)

(7)

式(7)中β为正参数，调节正则化项对模型的惩罚。通过调节参数，在使回归系数矩阵C中不相关或弱相关属性收缩为零的同时，能使重要属性获得更大的系数权重。

秩最小化是一个非凸优化且NP问题，但秩约束目标函数是可解的，即全局解能够得到[15]。为了更好地优化低秩结构和有效考虑类别间关联结构，算法令C=XY，并且有低秩r，则目标函数为:

s.t. rank(XY)≤min(m,k)

(8)

式(8)中，A∈Rn×d,X∈Rd×r,Y∈Rr×d，重构的回归系数矩阵C、矩阵X、Y都是低秩结构。U、G分别表示聚类指示矩阵、聚类中心矩阵，‖.‖F表示矩阵弗罗贝尼乌斯范数。

1.2 目标函数优化

由于式(8)的前半部分是凸的，lF-范数虽然对噪声和离群数据较为敏感，但作为正则化项它是非光滑的，为了高效率地求解目标函数(8),本文通过固定不同矩阵依次优化的方法来最优目标函数(8)。首先将式(8)化简，如式(9)所示。

βTr(YTXTDXY)

(9)

式(9)中D∈Rd×d为对角矩阵，其每个元素定义如式(10)所示。

(10)

ci表示矩阵C*=X*Y*的第i行，X*、Y*、C*分别为X、Y、C的最优解。

本文通过固定不同矩阵，依次优化对应矩阵，逐步实现最优目标函数的目的，其具体操作过程如下。

(1) 固定矩阵X、Y、G，优化矩阵U

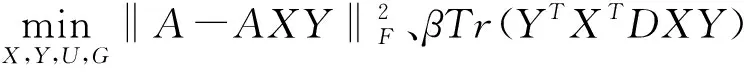
(11)

根据式(11)可知，经AXY原始数据转换后，再K均值处理，可使转换后的数据都分配到标签。

(2) 固定矩阵U、X、Y,优化矩阵G

当固定矩阵U、X、Y后，对式(9)的优化矩阵G求偏导数，并令所得偏导数为零。

(12)

(3) 固定矩阵U、G,优化矩阵X、Y

固定矩阵U、G，将式(12)代入式(9)中，并令式(9)等于E，可得:

(13)

通过上述化简，目标函数(8)就转化为:

(14)

令H=ATA-αATU[(UTU)-1]TUTA+αATA+βD，通过优化矩阵X、Y，同时证明本文算法具有执行线性判别分析[16](linear discriminant analysis, LDA)的特点。

1.3 目标函数推理

经过1.2节的目标函数优化，将式(8)转化为式(14)，但通过式(14)无法求解函数的最优值，本节通过对式(14)继续推理，以期证明式(14)具有执行LDA过程的特点，构建全局最优与属性向量间的桥梁。

固定聚类指示矩阵U和聚类中心矩阵G，对式(14)中的Y求偏导数，并令偏导数为零，如式(15)所示。

(15)

由式(15)可得YT=ATAX[(XTHX)-1]T，把得到的矩阵YT和Y代入式(14)中，有:

(16)

根据式(16)的推导，目标函数E只含有变量X，优化问题转化如下:

其中Qt和Qb分别表示LDA类内矩阵和类间离散度矩阵。通过求解式(17)可得矩阵X的最终表达式如式(19)所示。

(19)

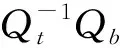
由于系数矩阵最优解C*=X*Y*的列空间和X的列空间相同，所以本文提出方法与正则化LDA具有同样的列空间。

2 本文算法及其收敛性

本文借鉴聚类算法、子空间学习和属性选择各自的优点，提出一种有效的属性选择算法。在线性回归的模型框架中有效地嵌入自表达方法,利用K均值聚类产生伪类标签最大化类间距以更好地对结构进行稀疏化处理；运用l2,p-范数考虑属性及其对应响应变量间的相关性，利用低秩约束来考虑不同类别间的相关性，消除数据冗余和不相关属性，以实现最优属性子集的选择。算法伪代码如下:

算法1: 本算法伪代码Input: 训练数据集A;正则化参数α,β;支持向量机参数(m,g)∈[-10: 2: 10];步骤1: 初始化分类器,类型选择线性模式;步骤2: 通过自表达方法得到自表达矩阵A;步骤3: 根据模型(8): 调用算法2求解全局最优解,以求自表征矩阵C*=X*Y*;步骤4: 利用最优解C*对原始属性集A进行属性选择,利用得到属性集更新样本属性集;步骤5: 采用支持向量机对新属性样本分类;Output: 分类准确率。

算法2: 优化求解式(8)的伪代码Input: 数据集A;参数α,β,r聚类中心数m;控制参数p;步骤1: 初始化 t=0,矩阵X(t)和Y(t),得到初始化C(t)=X(t)Y(t);步骤2: 利用K均值算法初始化矩阵U(t),初始化D(t)∈Rd×d; Do 步骤3: 通过公式(11)计算U(t+1); 步骤4: 通过公式(12)计算G(t+1); 步骤5: 通过公式(15)计算Y(t+1); 步骤6: 通过公式(19)计算X(t+1); 步骤7: 更新对角矩阵D(t+1),利用公式(10)计算第i个对角元素,ci=[X(t+1)Y(t+1)]i,t=t+1;While 目标函数(8)收敛;Output: 矩阵X,Y,聚类指示矩阵U。

对于迭代算法，收敛性是算法是否健壮有解的性能指标，对于本文提出的目标函数式(8)和其中的正则化项都非平滑，并且式中需要优化四个变量，求解目标函数最优解难度颇大，但首先要证明本算法是否收敛。

当迭代次数为t时，根据算法2中的步骤可知:

当迭代次数为t+1时，根据式(11)规则固定矩阵更新优化U(t+1)，可得如下不等式:

(22)

当迭代次数为t+1时，根据公式(14)规则固定矩阵U(t+1)，优化更新矩阵X(t+1)、Y(t+1)、G(t+1)可得如下不等式:

(23)

联合不等式(22)和(23)可得:

(24)

通过式(24)可知，目标函数是单调递减的，因此多次迭代后可收敛。

3 仿真实验分析

3.1 实验数据集

将本文算法、NFS(non feature selection)算法、LDA算法[16]、RFS算法[17]和RSR算法[18]等五种算法在BASEHOCK、PCMAC、Smk-can、ecoli-uni、CNAE-9、warpPIE10六个数据集上进行仿真，其中数据集ecoli-uni和CNAE-9属于UCI[19]，Smk-can、PCMAC、BASEHOCK、warpPIE10来自数据集[20]，数据集详见表1。

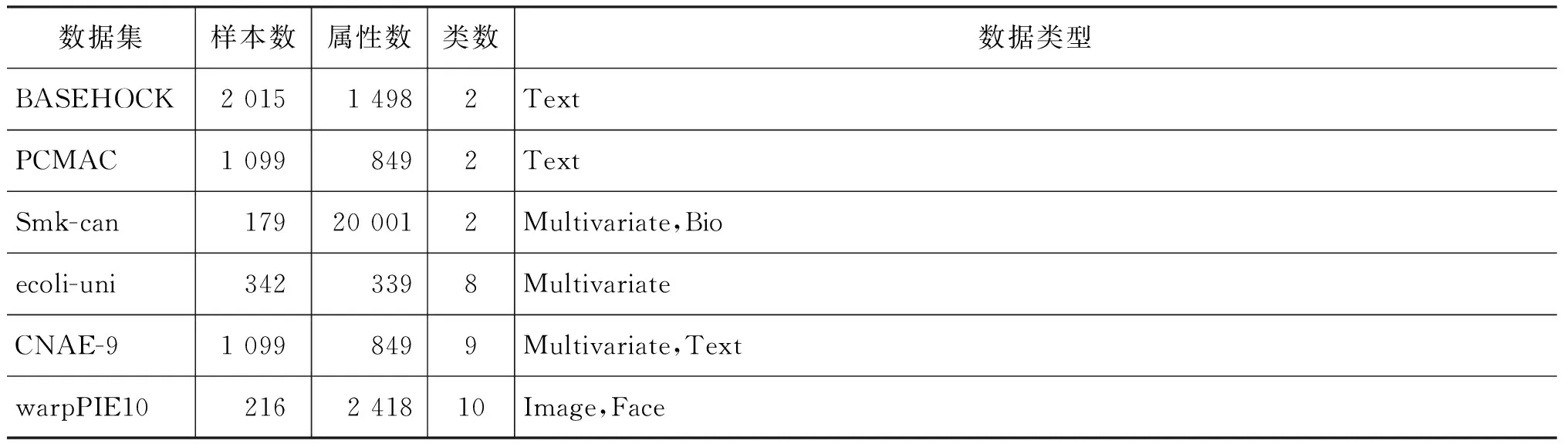
表1 数据集信息统计

仿真实现的环境及配置如下: 仿真是在Windows 7系统下，CPU: i3-3240@3.4GHz,RAM: 4GB，使用Matlab 2014a软件进行编程实现。

3.2 实验结果和分析

本文采用十折交叉验证法将原始数据分成训练集和测试集，再利用SVM进行分类，同时，把需要定义作为评价指标，即分类准确率越高表示算法效果越好。所有算法均保证在同一实验环境下进行，最后提取十次运行的实验结果的均值加减均方差来评估各算法的性能，以此评估实验的稳定性，各算法在数据集上的结果如图1所示。

通过图1(a)～(f)可以得出: 随着交叉验证次数的增加，本文算法在有些数据集上的分类准确率并不是最好的，但经过十次实验得到的平均准确率要比其他四种算法高。为了更直观地对比各算法的分类准确率，将各算法的分类准确率(均值±方差)统计结果列表，如表2所示。通过分析表2可以发现在所测试的六个数据集上，本文算法分类准确率均好于其他四种对比算法。与NFS算法、文献[16]、文献[17]和文献[18]相比，分类准确率平均提高了17.04%、13.95%、3.6%和9.39%。

从方差上看，本文算法的方差在大多数数据集上是最小的，说明算法分类准确率是稳定的。但在数据集CNAE-9上，文献[18]的方差要比本文算法的方差小4.2%，但分类准确率却高出文献[18] 9.39%，总体上好于文献[18]。作为有监督属性选择算法的文献[17]，因其利用现有的类标签在类少数据集上取得了较好的分类结果，平均分类准确率为84.17%，尤其在多类数据集上，文献[17]相比其他三种算法不仅利用伪类标签进行分类，还利用线性判别分析数据间相关性，利用数据相关性甄别最优属性子集。文献[18]利用原始数据得到的自表达系数矩阵嵌入稀疏学习模型中进行属性选择，但由于算法为无监督属性选择，实际分类效果一般，平均分类准确率仅为79.32%。本文算法在线性回归的模型框架中有效地嵌入自表达方法,同时利用K均值聚类产生伪类标签最大化类间距，以更好地对结构进行稀疏化处理，并利用稀疏学习方法中的l2,p-范数参数p灵活控制结果的稀疏性，取得了较高的分类准确率，实际平均分类准确率为87.54%。

图1 各算法在不同数据集上的结果

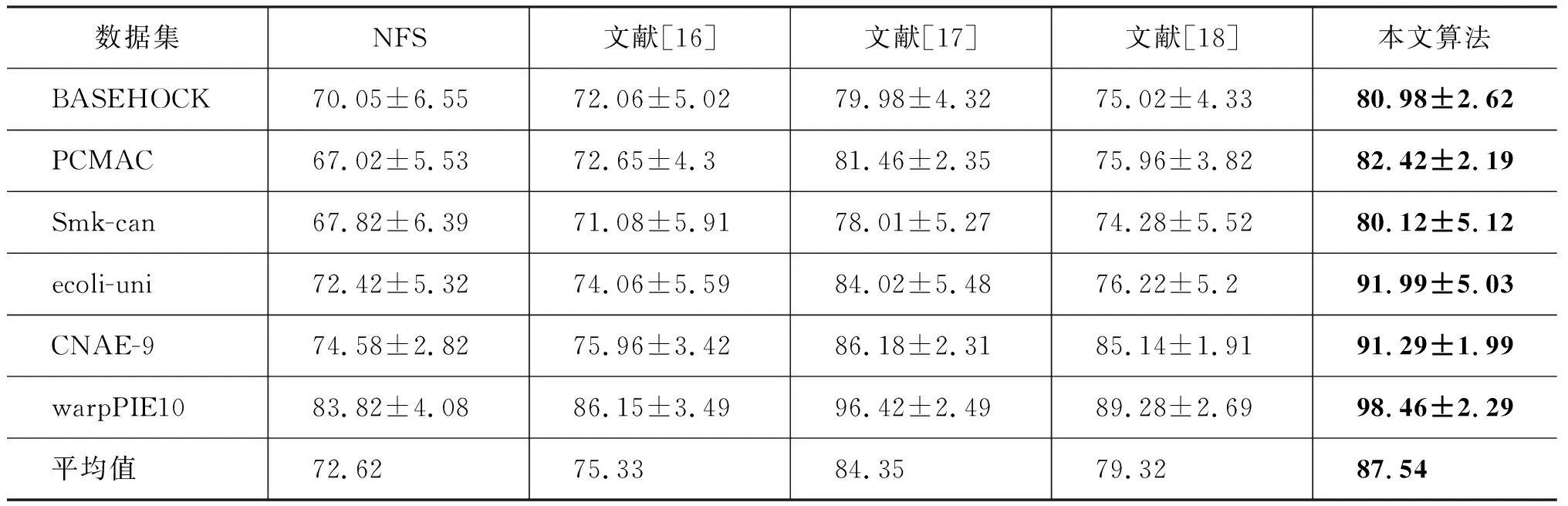
表2 分类准确率(均值±方差)的统计结果单位: %

不同数据集有不同的数据分布和干扰因素，像ecoli-uni、CNAE-9、warpPIE10等多类数据集，可通过控制秩大小来得到分类识别率，本文在数据集上的分类结果如下:

通过图2(a)～(c)结果可知，具有低秩约束的本文算法相比满秩得到的分类结果更优，结合表2综合分类结果可以看出，在多类数据集上，本文算法具有更佳的分类准确率和稳定的识别率，这是由于本文算法不仅能提取到数据集的重要属性，还能利用子空间学习对重要属性进一步微调，保证了数据自身结构。

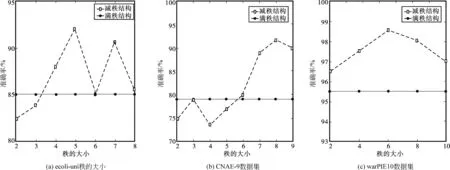
图2 多类数据集分类结果

4 结束语

对无监督属性选择算法无类别信息和未考虑属性的低秩问题，本文提出一种新属性选择算法。算法使用原始数据构建自表达矩阵，并融合K均值聚类、低秩属性选择和子空间于模型中，利用K均值聚类补充无监督选择的缺陷，同时扩展子空间学习在回归模型上的应用，弥补属性选择在数据调整中的不足。经实验验证，与其他四种属性选择算法相比，本文算法不仅有较高的分类准确率，并且分类结果也最为稳定，特别相比满秩得到的分类结果更优。