基于违约状态联合概率的商业银行信贷资金行业间优化配置模型
曹勇 ,李孟刚 ,李刚,常友玲
(东北大学 秦皇岛分校1a.经济学院;1b.管理学院,河北 秦皇岛 066004;2.北京交通大学 中国产业安全研究中心,北京 100044)
商业银行信贷资金的优化配置是金融资产优化配置的一个特定领域,从金融资产优化配置决策所采用的方法看,非线性数学规划方法被经常采用。不同金融资产优化配置模型的差别,主要在所建立的目标函数或约束条件上具有特色。Alexander等[1]通过最小化投资组合收益率的方差建立了股票投资组合优化模型。Quaranta等[2]通过最小化投资组合的CVaR 值建立了股票投资组合的优化配置模型。刘艳萍等[3]通过最大化贷款组合的效用函数建立了银行贷款组合的优化配置模型。Brandtner[4]对比研究了最小化CVaR 与最小化组合收益率方差对投资组合优化配置决策的影响。
由于贷款组合的效用函数是一个关于贷款组合期望收益率的增函数和关于收益率方差的减函数,又由于无论是投资组合收益率的方差,还是投资组合的VaR 或CVaR 值都是反映投资组合收益率的波动幅度或分布特征,也就是投资组合的风险,所以计量贷款组合的收益率和风险是构建银行贷款组合优化配置模型的基础。Frey等[5]利用Bernoulli混合模型研究了信贷组合VaR 和CVaR 值的计算。Dietsch等[6]采用次序Probit模型和Gamma分布研究了法国中小企业贷款组合的风险计量。Lucas等[7]采用状态转换模型探讨了经济扩张和衰退情况下的信用转移矩阵及其对信贷组合风险的影响。Rosen等[8]研究了信贷组合风险产生的原因及其对风险的边际贡献。Tsaig等[9]探讨了信用迁移对银行贷款组合和债券组合价值方差的影响。
上述关于贷款组合风险计量方法的研究为银行贷款组合优化配置模型的构建奠定了基础。迟国泰等[10]在贷款组合收益率既定及VaR 约束条件下,通过最小化贷款组合收益率的方差建立银行贷款组合优化决策模型。郭战琴等[11]在VaR 约束下,通过最小化贷款组合收益率的方差和最大化贷款组合期望收益率建立贷款组合优化的多目标规划模型。刘艳萍等[3]在VaR 约束下,通过最大化贷款组合的效用函数建立银行贷款组合的优化配置模型。洪忠诚等[12]利用信用风险迁移矩阵,通过最小化贷款组合的CVaR 值建立银行贷款组合的优化模型。
现有贷款组合优化配置模型的研究取得了长足进展,但仍然存在需要进一步深入研究的问题。现有商业银行信贷组合优化配置模型多是探讨银行信贷资金在公司间的优化配置,这类研究对于商业银行同时对多家公司进行贷款的决策问题具有重要参考意义,但现有研究很少探讨商业银行信贷资金如何在行业之间进行优化配置。
本文在现有研究基础上,进一步探讨银行信贷资金在行业间的优化配置问题,从而使商业银行信贷资金在整体上达到最优。本文的创新与特色在于:以行业内代表性上市公司市值加权的股票价格作为行业平均股价,以市值加权的每股负债作为行业平均每股负债。根据行业平均股价与行业平均每股负债,应用KMV 模型计算行业违约概率,解决了行业违约概率不能直接计算的难题。在应用KMV模型计算行业违约概率的基础上,利用正态Copula函数计算m个行业2m种违约状态的联合违约概率,解决了行业违约状态的联合概率因不可直接观测而难以计量的问题。以对m个行业的贷款权重为优化变量,以银行整体信贷资金的差异系数最小化为目标函数,建立基于违约状态联合概率的商业银行信贷资金行业间优化配置模型,求解出每个行业的最优贷款权重,能够使得银行整体信贷资金获取单位收益的风险最小。本文构建的基于违约状态联合概率的商业银行信贷资金行业间优化配置模型,对于商业银行信贷资金在行业间的优化配置与风险管理具有重要参考意义。
1 基于违约状态联合概率的商业银行信贷资金行业间优化配置模型构建原理
1.1 研究目标
商业银行在贷款发放过程中,既需要在微观上考虑对哪些公司贷款及贷款比例为多少,能够使得贷款风险一定时收益最大,或收益一定时风险最小;也需要在宏观上控制信贷资金在各行业间的配置比例,从而分散贷款的集中度,在保证信贷资金收益率的同时降低风险,使得商业银行信贷资金在整体上达到最优。
本文构建了基于违约状态联合概率的商业银行信贷资金行业间优化配置模型,为银行信贷资金在行业间的优化配置提供决策参考。
1.2 开展研究的难点
(1)行业违约风险难以计量。现有违约风险计量模型,如Logistic、KMV、Credit Risk+、Credit Metrics等模型,均是针对公司或上市公司,其违约风险计量的依据是公司财务指标或上市公司的股票价格与每股负债等。而对于行业而言,既不存在确定的财务指标值,也无对应的股票价格与每股负债。因此,行业违约风险难以计量,而违约风险的计量又是贷款定价与信贷资金优化配置的基础参数。
(2)行业间违约状态的联合概率不可观测。违约状态指在m笔贷款到期时,每笔贷款是否如期偿付本息的状况,由于每笔贷款均存在到期违约的可能性,即每笔贷款到期时均存在违约或不违约两种状态,故理论上在m笔贷款到期时共有2m种违约状态。将每一种违约状态可能发生的概率称为违约状态的联合概率。由于行业间违约状态的联合概率实际不可观测,故违约状态联合概率的测算存在困难。
(3)银行信贷资金收益率波动的分布特征难以确定。在上述不同的违约状态下,银行信贷资金的收益率是变化的,如果能够确定信贷资金收益率的分布特征,则可据以计算银行信贷资金收益率的方差、VaR 或CVaR 值等,进而可构建银行贷款资金优化配置模型。但是由于行业间违约状态的联合概率不可直接观测,故银行信贷资金收益率的期望及其方差难以计算,亦即银行信贷资金收益率的分布特征难以确定。
1.3 解决难点的思路
(1)行业违约风险计量的思路。将行业视为行业内代表性上市公司的加总,以行业内代表性上市公司市值加权的股票价格作为行业平均股价,以市值加权的每股负债作为行业平均每股负债。根据行业平均股价与行业平均每股负债数据,应用KMV模型计算行业违约概率,解决行业违约风险难以计量的问题。
(2)行业间违约状态联合概率测算的思路。将商业银行对m个行业的贷款在到期时区分为2m种违约状态。例如银行对A 和B两个行业贷款,则在贷款到期时,有2m=22=4种违约状态,分别为:A、B行业均不违约、A 行业违约而B行业不违约、A 行业不违约但B行业违约、A、B行业均违约。在上述应用KMV模型计算行业违约概率的基础上,再应用正态Copula函数计算各违约状态的联合概率,从而解决行业间违约状态联合概率不可直接观测的问题。
(3)银行信贷资金收益率分布特征确定的思路。将行业违约概率与贷款违约损失率的乘积作为对该行业贷款的信用风险溢价。在银行贷款基准利率的基础上再加上行业贷款信用风险溢价,作为对该行业贷款的贷款利率。在贷款到期时,如行业不违约,则对该行业贷款的收益率为贷款利率;如违约,则贷款的收益率为负且其值等于违约损失率。根据2m种违约状态下整体信贷资金的收益率及各违约状态的联合概率,确定银行整体信贷资金收益率波动的分布特征,从而解决银行整体信贷资金收益率分布特征难以确定的问题。
在上述解决难点思路的基础上,构建基于违约状态联合概率的商业银行信贷资金行业间优化配置模型,方法为:根据2m种违约状态下整体信贷资金的收益率及各违约状态的联合概率,计算银行整体信贷资金收益率的期望及其方差,进一步计算银行整体信贷资金的差异系数,即信贷资金获取单位收益所承担的风险。将银行全部信贷资金视为单位1,以对m个行业的贷款权重为优化变量,以银行整体信贷资金的差异系数最小化为目标函数,建立基于违约状态联合概率的商业银行信贷资金行业间优化配置模型,为商业银行信贷资金在行业间的优化配置提供决策参考。
基于违约状态联合概率的商业银行信贷资金行业间优化配置模型构建原理如图1所示。

图1 基于违约状态联合概率的商业银行信贷资金行业间优化配置模型构建原理图
2 基于违约状态联合概率的商业银行信贷资金行业间优化配置模型
2.1 行业平均股价与平均每股负债的计算
2.1.1 行业平均股价的计算假设某行业有n家代表性上市公司。记Pi为第i个代表性上市公司的股票价格,Qi为第i个代表性上市公司的股票数量,w i为第i个上市公司的市值在n家代表性上市公司总市值中所占的权重(i=1,2,…,n),则有
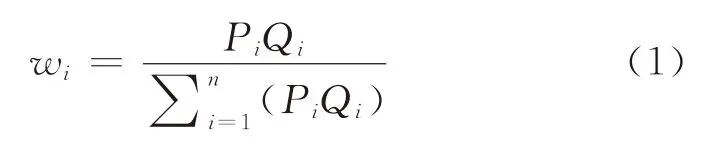
根据行业内n家代表性上市公司的股票价格P i及以市值计算的权重w i,可计算得到行业平均股票价格。记P为该行业的平均股票价格,则有
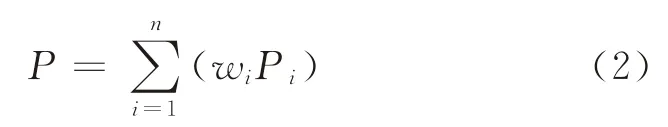
式(2)的经济学含义:行业的平均股票价格等于行业内代表性上市公司的股票价格与其根据市值计算的权重的乘积之和。
2.1.2 行业平均每股负债的计算 记STDi为行业内第i家代表性上市公司的每股短期负债,STD为该行业的平均每股短期负债,则有
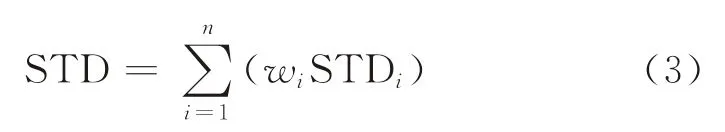
式(3)的经济学含义:行业平均每股短期负债等于行业内代表性上市公司的每股短期负债与其根据市值计算的权重的乘积之和。
类似地,记LTDi为行业内第i家上市公司的每股长期负债,LTD 为该行业的平均每股长期负债,则有

式(4)的经济学含义:行业平均每股长期负债等于行业内代表性上市公司的每股长期负债与其根据市值计算的权重的乘积之和。
2.2 行业平均每股资产价值及资产收益波动率的计算
2.2.1 行业平均每股收益波动率的计算 行业平均每股收益率是指根据行业平均股票价格计算的每股收益率。记Pt为某行业在t时期的平均股票价格,rt为该行业在t时期的平均每股收益率,则有[13]

式(5)的经济学含义:t时期的行业平均每股收益率r t等于t时期的行业平均股价P t取自然对数后的1阶差分。
记T为考察的行业平均每股收益率的期间数为该期间行业平均每股收益率的均值,σS为某行业平均每股收益波动率,则有[14]
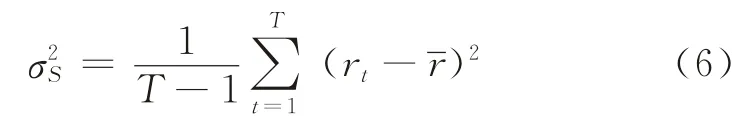
式(6)的经济学含义:行业平均每股收益波动率σS为行业平均每股收益率r t的标准差。
计算行业平均每股收益波动率的作用是通过行业平均股票价格和行业平均每股收益波动率计算行业平均每股资产价值及每股资产收益波动率。
2.2.2 计算行业平均每股资产价值及资产收益波动率的联立方程 由于上市公司财务报表中资产价值核算的是公司资产的历史成本,并不能准确地反映公司资产的市场价值。为解决该问题,KMV 模型通过上市公司的股票价格及股票收益波动率来测算公司的资产价值及资产收益波动率。其测算原理是将上市公司股票价值视为以公司资产价值为标的资产,以公司负债为执行价格的看涨期权价值,从而构建计算上市公司每股资产价值及资产收益波动率的联立方程[13]。
本文将行业视为行业内代表性上市公司的加总,因此,将行业平均股票价格替代KMV 模型中的上市公司股票价格,将行业平均每股负债替代KMV 模型中的公司每股负债,应用KMV 模型的原理和方法,测算行业违约概率,从而解决行业违约概率不可观测的难题。
记S为行业平均股票价格,σS为行业平均每股收益波动率,V为行业平均每股资产价值,σV为行业平均每股资产收益波动率,D为行业平均每股负债,rf为无风险利率,N(·)为标准正态分布的累积概率分布函数,则有[13]
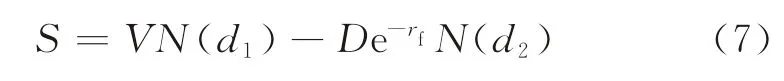
式中:

式(7)为Black-Scholes期权定价公式,其经济学含义为:行业平均股票价格S等于行业平均每股资产价值与以d1为参数的标准正态累积概率的乘积VN(d1)减去行业平均每股负债D与以d2为参数的标准正态累积概率乘积DN(d2)以无风险利率rf折现后的差。
为求解式(7)中V及σV这两个未知变量,KMV模型引入股票收益波动率σS与资产收益波动率σV,两者之间存在如下函数关系[13]:
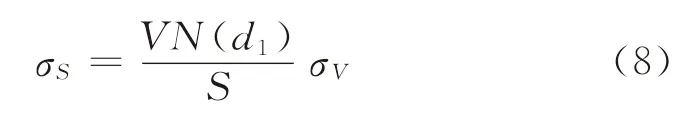
式(8)中各符号的含义同前。式(7)、(8)联立构成非线性方程组,解此非线性方程组可计算得到行业平均每股资产价值及每股资产收益波动率。
2.2.3 求解联立方程的算法 利用Newton迭代法可求解式(7)、(8)联立构成的非线性方程组,为此构造函数分别为[14]:

求解行业平均每股资产价值V与每股资产收益波动率σV的迭代公式为[14]

式中:V0为行业平均每股资产价值的给定初值;σV0为每股资产收益波动率的给定初值。应用式(11)多次迭代可计算行业平均每股资产价值V及每股资产收益波动率σV。迭代停止的条件是相邻两次迭代结果的误差足够小,如小于10-5。
利用Newton迭代算法求解式(7)、(8)联立构成的非线性方程组,计算得到行业平均每股资产价值V及每股资产收益波动率σV,为进一步采用KMV 模型计算行业违约概率奠定了基础。
2.3 基于KMV 模型与正态Copula函数的行业违约状态联合概率的计算
2.3.1 基于KMV 模型的行业违约概率测算
KMV 模型根据上市公司资产价值、公司负债和公司资产收益波动率计算公司违约距离,再通过违约距离计算公司违约概率[13]。
本文将行业平均每股资产价值替代KMV 模型中的上市公司每股资产价值,将行业平均每股负债替代公司每股负债,将行业资产收益波动率替代上市公司资产收益波动率,再利用KMV 模型的方法计算行业违约概率。
记STD 为行业平均每股短期负债,LTD 为行业平均每股长期负债,D为行业违约临界点,KMV模型将违约临界点D设定为短期负债STD 加γ倍的长期负债LTD[13],即
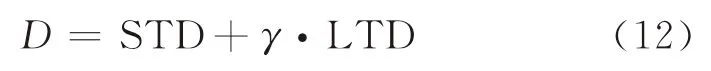
式(12)的经济学含义:行业违约临界点D等于行业平均每股短期负债STD 加上行业平均每股长期负债LTD 乘以折扣系数γ值后的和。
根据穆迪KMV 公司的统计数据,当公司资产价值低于其短期负债加0.5倍的长期负债时,公司违约最为频繁,故取γ=0.5[13]。由于本文将行业视为行业内代表性上市公司的加总,故对行业违约临界点的测算也取γ=0.5。
记V为行业平均每股资产价值,σV为行业平均每股资产收益波动率,DD为行业违约距离。根据KMV 模型,行业违约距离[13]

式(13)的经济学含义:行业违约距离DD等于行业平均每股资产价值V减去行业违约临界点D的差,再除以行业平均每股资产价值V与行业平均每股资产收益波动率σV之积的商。
在假定行业平均每股资产价值V服从正态分布的条件下,行业违约概率为[13]
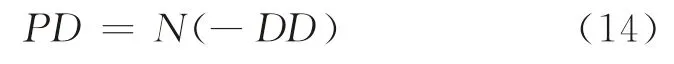
式中,N(·)为标准正态分布的累计概率分布函数。
式(14)的经济学含义:行业违约概率PD等于以负的行业违约距离DD为参数的标准正态分布的累计概率。查标准正态累积概率分布表,可得到给定参数-DD的概率值。由式(14)可知,DD与PD呈反向变化关系,DD越大,PD越小。
根据行业平均每股资产价值、行业平均每股负债和行业每股资产收益波动率计算行业违约距离,再通过行业违约距离计算行业违约概率,解决了行业违约概率不可观测的问题。
2.3.2 行业违约距离之间相关系数矩阵的计算 在所考察的某段时期内取T个时间点,在每个时间点上,应用式(13)计算m个行业的违约距离。
记DD kt为第k个行业在第t个时点上的违约距离,DD jt为第j个行业在第t个时点上的违约距离,其中,k=1,2,…,m,j=1,2,…,m,t=1,2,…,T。记ρkj为第k、j个行业违约距离的相关系数,则有

应用式(15)可计算出任意两个行业违约距离之间的相关系数,从而得到m个行业违约距离之间的相关系数矩阵,并记R=[ρkj]m×m为m个行业违约距离的相关系数矩阵。
2.3.3 基于正态Copula函数的行业违约状态联合概率的计算 由于对每一个行业的贷款在到期时均有违约和不违约两种状态,故对m个行业贷款的违约状态共有2m种。
对于单个行业的违约概率可用式(12)~(14)中的KMV 模型计算。
由于KMV 模型采用正态分布完成从违约距离到违约概率的计算(见式(14)),故本文采用正态Copula函数计算m个行业2m种违约状态的联合概率。
用s=1,2,…,2m分别标记m个行业的2m种违约状态;记JPDs为第s种违约状态的联合概率,则违约状态联合概率为[15]
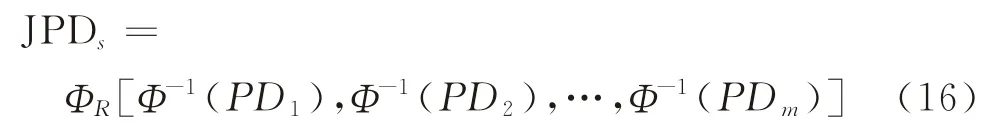
式中:R=[ρkj]m×m为m个行业违约距离的相关系数矩阵;ΦR(·)为以相关系数矩阵R为参数的m维正态分布的联合概率分布函数;Φ-1(·)为1维标准正态分布函数的逆函数。
由式(14)可知,-DD=Φ-1(PD),故式(16)可变形为
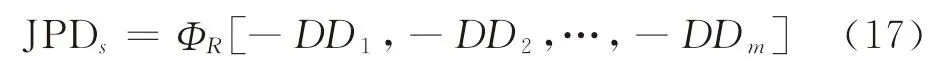
调用Matlab 软件中的多元正态分布函数mvncdf()可方便地计算出第s种违约状态的联合违约概率JPDs。
计算m个行业违约状态联合概率的作用是为进一步计算对m个行业贷款的贷款组合收益率均值和方差奠定基础。
2.4 基于违约状态联合概率的商业银行信贷资金行业间优化配置模型
2.4.1 基于信用风险溢价的行业贷款利率的计算 记rk为银行对第k个行业的贷款利率,rb为商业银行贷款的基准利率,PD k为第k个行业根据KMV 模型计算的行业违约概率,LGD 为银行贷款的违约损失率,则有
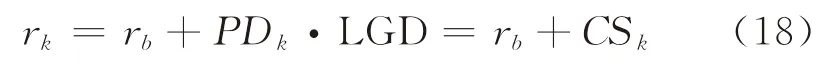
式中:右端第1项为银行贷款的基准利率rb;第2项为第k个行业的违约概率PD k乘以银行贷款的违约损失率LGD,称为银行对第k个行业贷款的信用风险溢价CS k。
式(18)的经济学含义:对第k个行业贷款的利率等于银行贷款的基准利率加上对第k个行业贷款的信用风险溢价。根据式(18)确定行业贷款利率的好处是能够使行业违约风险导致的期望损失在贷款利率中得到补偿。
2.4.2 贷款组合收益率均值、方差与差异系数的计算 设银行同时对m个行业贷款,记rk为银行对第k个行业贷款的利率,由式(18)计算得到。将银行整体信贷资金设为1,并设w k为银行对第k个行业贷款的权重,显然,有约束成立。
为简单起见,假设对m个行业贷款的到期日相同,且期限均为1年。用示性函数I(s,k)表示在第s种违约状态下第k个行业是否违约,如果在第s种违约状态下第k个行业违约,则I(s,k)=1;否则,I(s,k)=0。其中,s=1,2,…,2m,k=1,2,…,m。
记rps为银行整体信贷资金在第s种违约状态下的收益率,则有

如果在第s种违约状态下,第k个行业不违约,则I(s,k)=0,且1-I(s,k)=11,即式(19)右端大括号中起作用的项变为rk,即银行对第k个行业的贷款到期时获得r k的收益率。
如果在第s种违约状态下,第k个行业违约,则I(s,k)=1,且1-I(s,k)=0,即式(19)右端大括号中起作用的项变为-LGD,即银行对第k个行业的贷款到期时损失LGD。
综上所述,式(19)的经济学含义为:在第s种违约状态下,银行整体信贷资金的收益率r ps等于对m个行业贷款的收益率rk或损失率-LGD的加权和。
记E(rp)为银行整体信贷资金在2m种违约状态下的期望收益率,JPDs为第s种违约状态的联合概率(见式(17)),则有
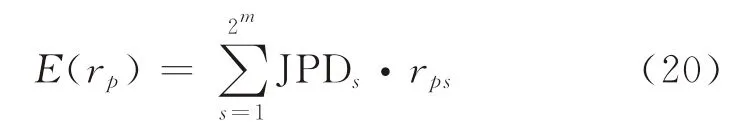
式(20)的经济学含义为:银行整体信贷资金的期望收益率E(rp)等于2m种违约状态的联合概率JPDs与该违约状态下银行整体信贷资金收益率r ps的乘积和。
记var(rp)为银行整体信贷资金收益率的方差,则由统计学中方差的计算公式易得
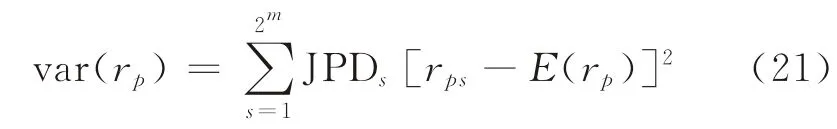
从而,银行整体信贷资金收益率的标准差为
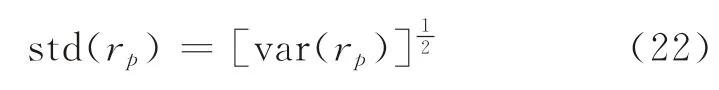
记θ为银行整体信贷资金收益率的差异系数,由差异系数的定义[3],有

式(23)的经济学含义:银行整体信贷资金的差异系数θ等于银行整体信贷资金收益率的标准差std(rp)除以银行整体信贷资金的期望收益率E(rp)。银行整体信贷资金的差异系数θ反映了银行通过对m个行业发放贷款,获得单位收益率所承担的风险大小。差异系数越大,说明银行获得单位收益率所承担的风险也越大。
2.4.3 基于违约状态联合概率的商业银行信贷资金行业间优化配置模型 当商业银行整体信贷资金中对各行业的贷款权重w k变化时,银行整体信贷资金的期望收益率E(rp)及其标准差std(rp)、银行整体信贷资金的差异系数θ也相应变化。
以银行整体信贷资金中对m个行业的贷款权重w k为决策变量;以最小化银行整体信贷资金的差异系数θ为目标函数;以银行整体信贷资金的期望收益率E(rp)大于或等于目标收益率ro、贷款权重大于或等于0、且贷款权重之和等于1为约束条件,构建银行信贷资金行业间优化配置模型:
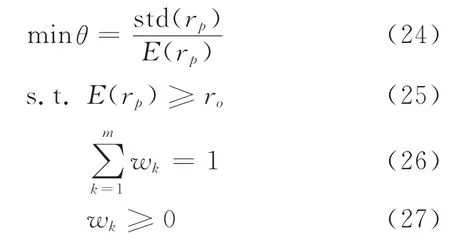
目标函数式(24)通过最小化商业银行整体信贷资金的差异系数θ,能够使银行整体信贷资金获取单位收益率所承担的风险达到最小。约束条件式(25)使银行整体信贷资金的期望收益率大于或等于目标收益率;式(26)使银行信贷资金全部贷放出去;式(27)使银行对任一行业的贷款为非负值。
式(24)~(27)可使用Matlab软件的优化工具箱或Excel软件的规划求解等多种软件求解。通过求解式(24)~(27),可得到对每个行业贷款的最优权重,为商业银行信贷资金在行业间的优化配置提供决策参考。
3 基于违约状态联合概率的商业银行信贷资金行业间优化配置模型算例
3.1 样本选取
选取机械设备业、建筑业、金属非金属业、运输仓储业和批发零售业5个行业作为样本行业,每个样本行业均选取4家代表性样本公司,共20家样本公司,如表1所示。
3.2 行业平均股价与平均每股负债的计算
3.2.1 行业平均股价的计算 20家样本上市公司2011年的股票周收盘价格如表2所示。表2 中样本上市公司股票周收盘价格来自Wind资讯金融终端。鉴于篇幅,表2仅列出了部分样本上市公司股票的部分周收盘价格。

表1 样本行业与样本公司名称

表2 上市公司股票周收盘价格
根据上市公司市值计算的样本公司在行业中的权重如表3所示。以表3 许继电器平均股价14.586 1 元/股为例,说明样本公司平均股价的计算过程。将表2许继电器51个周的周收盘价格取平均值,可计算得到许继电器平均股价为14.586 1元/股。表3第3列其他数据的计算类推,不赘述。

表3 根据上市公司市值计算的样本公司权重
以表3 许继电器在机械设备业中的权重等于0.063 0为例,说明样本公司在行业中所占权重的计算过程。将表3机械设备业4家样本公司的平均股价及其股本总数代入式(1),可计算得到许继电器在机械设备业中的权重等于0.063 0。表3第5列其他数据的计算类推。
根据行业内代表性上市公司的股价及其权重,可计算得到行业平均股价、及行业平均每股收益率,计算结果如表4所示。

表4 行业平均股价及行业平均每股收益率
以表4中机械设备业在2011年1月7日的平均周收盘股价10.365 3元/股为例,说明行业平均股价的计算过程。将表2中许继电器、云内动力、特变电工和中国北车的周收盘价格,及表3中上述4家上市公司的公司权重代入式(2),可计算得到机械设备业在2011 年1 月7 日的平均周收盘股价为10.365 3元/股。表4第3~7列的行业平均股价的计算过程类推。
由于每股收益率的计算需要用到本期及上一期的股票价格,故第1周2011年1月7日对应的每股收益率没有计算,即表4第1行第8~12列的数据为空。
以表4中机械设备业在2011年1月14日的平均每股收益率-0.033 4为例,说明行业平均每股收益率的计算过程。将表4 中机械设备业在2011年1月14日和2011年1月7日的周收盘价格代入式(5),可计算得到机械设备业的平均每股收益率为-0.033 4。表4第8~12列的行业平均每股收益率的计算过程类推。
3.2.2 行业平均每股负债的计算20家样本上市公司的每股短期负债与每股长期负债数据如表5所示。表5中第3、4列的数据来自Wind资讯金融终端。以表5中许继电器违约临界点D=9.696 0元/股为例,说明上市公司违约临界点的计算过程。将表5中许继电器每股短期负债、每股长期负债及参数γ=0.5[13]代入式(12),计算得到许继电器违约临界点D=9.696 0元/股。表5第5列其他数据的计算类推。
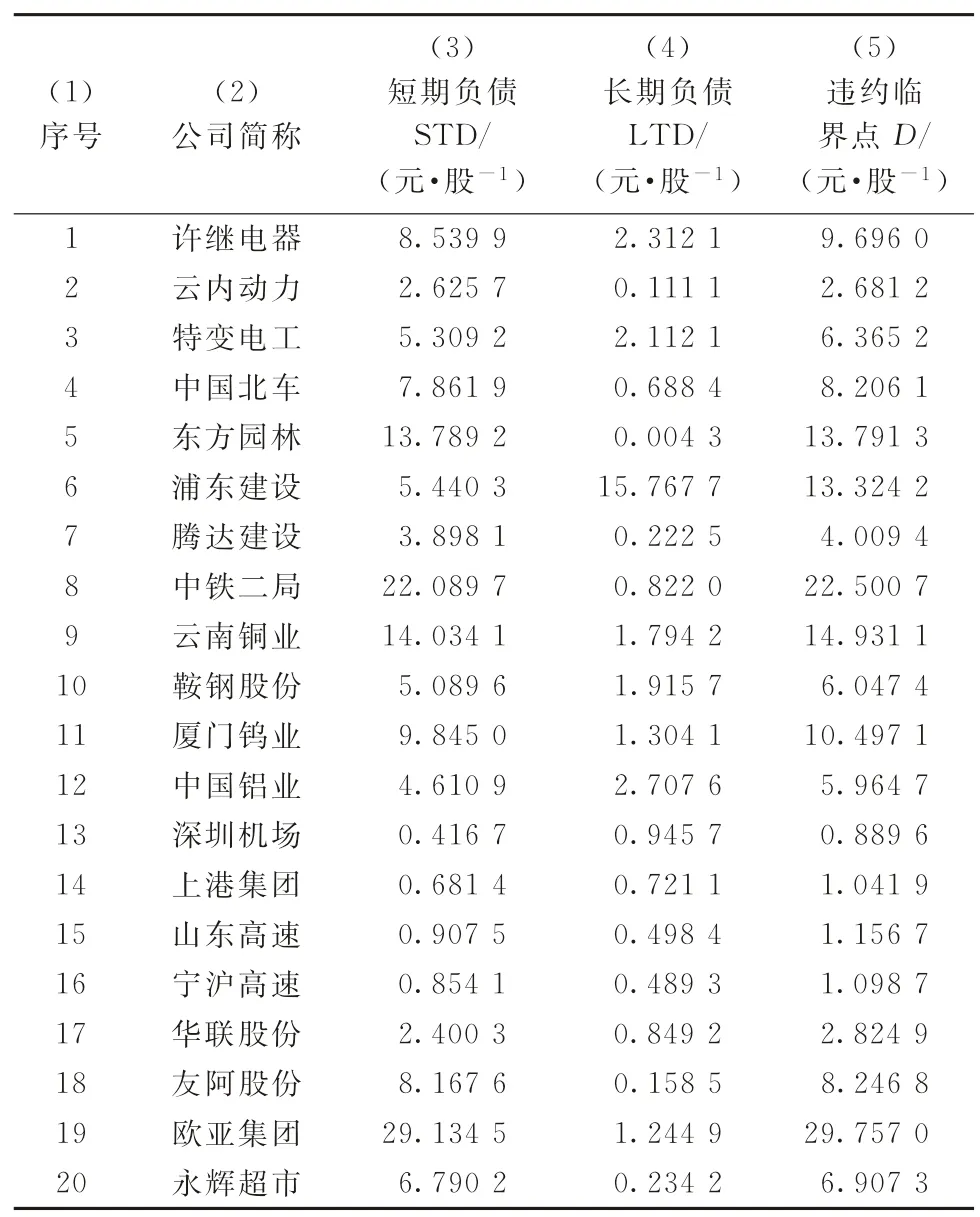
表5 样本上市公司的每股负债
3.3 行业平均每股资产价值及资产收益波动率的计算
3.3.1 行业平均每股收益波动率的计算根据行业平均股价S、行业平均每股收益波动率σS求解式(7)、(8),可计算得到行业每股资产价值V及行业资产收益波动率σV,计算结果如表6所示。
以表6 中机械设备业加权股价的均值为8.484 5元/股为例,说明行业加权股价均值的计算过程。对表4 中机械设备业51 个周的加权股价取平均值,得到机械设备业加权股价的均值为8.484 5元/股。

表6 样本行业违约距离与违约概率
以表6 中机械设备业股票收益波动率σS=0.272 1为例,说明行业股票收益波动率的计算过程。将表4中机械设备业股票收益率及其均值、时期数T=50代入式(6),可计算得到机械设备业股票收益波动率σS=0.272 1。
以表6 中机械设备业违约临界点D=7.350 5元/股为例,说明行业违约临界点的计算过程。将表5中机械设备业代表性上市公司许继电器、云内动力、特变电工和中国北车的违约临界点分别与表3中上述4家上市公司的权重相乘,然后相加,计算得到机械设备业违约临界点D=7.350 5元/股。
3.3.2 行业平均每股资产价值及资产收益波动率的计算通过求解由式(7)、(8)构成的联立方程组,计算得到行业每股资产价值和资产收益波动率。
由于表6第6、7列的数据通过求解联立方程组同时得到,故一并说明其计算过程。以列机械设备业每股资产价值V=15.632 0元/股、资产收益波动率σV=0.147 7为例,说明行业每股资产价值和资产收益波动率的计算过程。
将表6中机械设备业的加权股价均值、股票收益波动率、违约临界点及无风险利率rf=0.028 0[16]分别代入式(7)、(8),利用式(9)~(11)所示的Newton迭代法,计算得到机械设备业每股资产价值V=15.632 0元/股、资产收益波动率σV=0.147 7。上述求解过程可利用Matlab软件求解非线性方程组的fsolve函数实现。
3.4 基于KMV 模型与正态Copula函数的行业违约状态联合概率的计算
3.4.1 基于KMV 模型的行业违约概率测算以表6中机械设备业违约距离DD=3.587 4为例,说明行业违约距离的计算过程。将表6中机械设备业的每股资产价值、资产收益波动率及违约临界点代入式(13),计算得到机械设备业违约距离DD=3.587 4。
以表6中机械设备业违约概率PD=0.000 167为例,说明行业违约概率的计算过程。将表6中机械设备业违约距离代入式(14),计算得到PD=0.000 167。
3.4.2 行业违约距离之间相关系数矩阵的计算应用正态Copula函数计算m个行业2m种违约状态的联合概率时,需用到m个行业违约距离之间的相关系数矩阵,为此,本文计算了5 个样本行业2011年4个季度的违约距离。计算结果如表7所示。
表7各列数据的计算过程与表6相应列数据的计算过程类似,只是计算的时间区间由年度变为季度。因此,表7各列数据的计算过程不赘述。
根据表7中5 个样本行业4 个季度的违约距离,利用式(15)可计算出违约距离的相关系数矩阵。但直接计算出的行业违约距离相关系数矩阵近似为奇异矩阵,不能直接应用于正态Copula函数计算m个行业2m种违约状态的联合概率。本文根据行业4 个季度的违约距离,首先计算出行业违约距离的均值与方差,然后根据行业违约距离的均值和方差并利用正态分布,每个行业随机生成20个违约距离,再应用式(15)计算违约距离的相关系数矩阵,可解决直接计算相关系数矩阵近似为奇异矩阵的问题。
鉴于篇幅,每个样本行业随机生成的20个违约距离略。5个样本行业违约距离之间的相关系数矩阵如表8所示。表8 所示的相关系数矩阵可利用Excel软件的correl()函数方便得到。
根据样本行业的违约距离及违约距离之间的相关系数矩阵,利用正态Copula函数可计算得到各违约状态的联合概率,结果如表9所示。
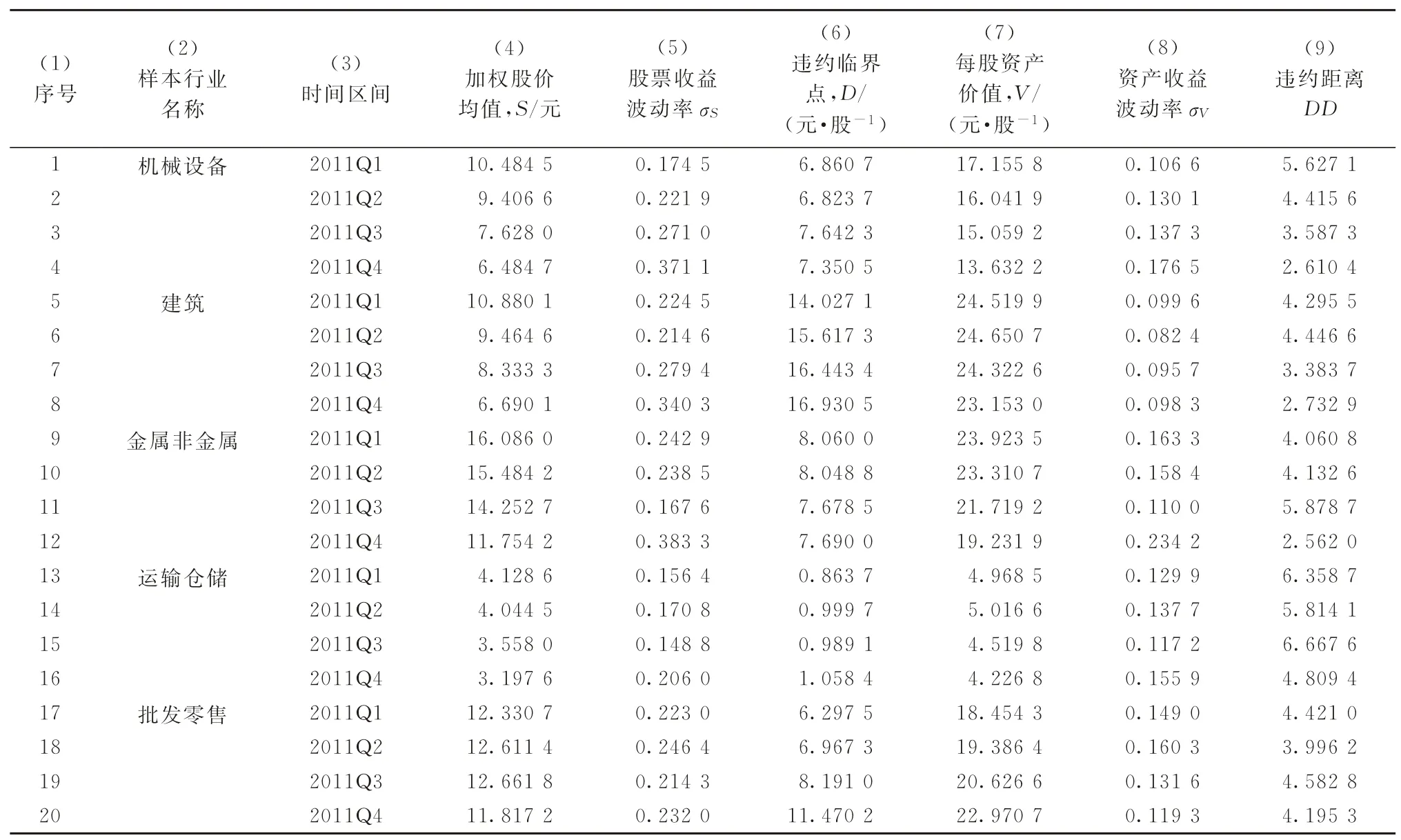
表7 样本行业季度违约距离

表8 行业违约距离的相关系数矩阵
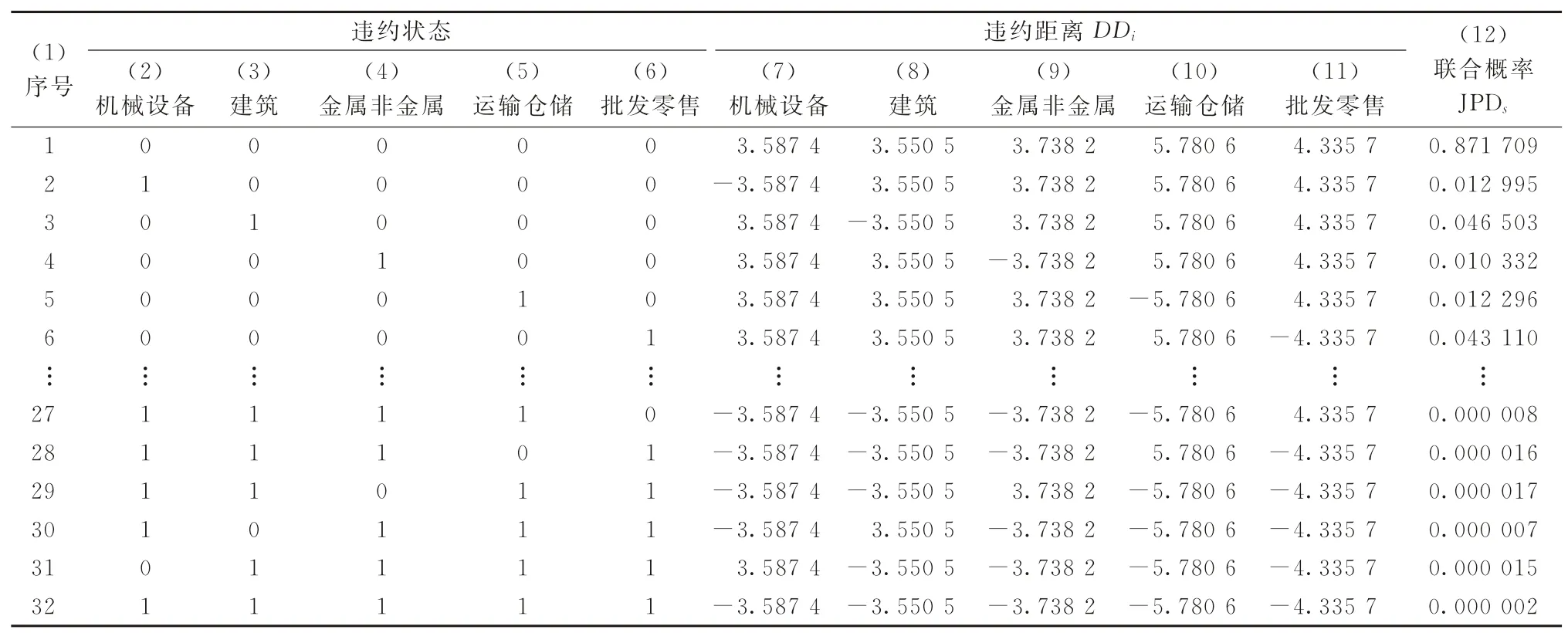
表9 样本行业的违约状态及其联合概率
3.4.3 样本行业的违约状态本文算例中共有5个样本行业,由于在贷款到期时,每个行业均存在违约或非违约两种可能的状态,故样本行业的违约状态共有25=32种,其中,“0”表示非违约,“1”表示违约。
表9第1行第2~6列表示在第1种违约状态下,5个样本行业的违约状况,由于表9 第1 行第2~6列的数据均为“0”,表示在第1种违约状态下,5个样本行业均不违约。表9第2行第2~6列为第2种违约状态下,5个样本行业的违约状况,由于表9第2行第2列的数字为“1”,表示在第2种违约状态下,机械设备在贷款到期时违约;而表9第2行第3~6列的数字为“0”,表示其他4个样本行业非违约,即在贷款到期时正常还本付息。
表9其他各行第2~6列表示在对应违约状态下,5个样本行业是否违约的“0”“1”标识的含义类推。特别地,在第32种违约状态下,表9第32行第2~6列数字均为“1”,表示在第32种违约状态下,5个样本行业均违约。限于篇幅,表9中仅列出了部分违约状态下各样本行业是否违约的标识。
3.4.4 各违约状态下样本行业的违约距离当某行业贷款到期时,根据KMV 模型,其违约概率PD=N(-DD),即式(14),其中,N(·)为标准正态分布的累积概率分布函数。因此,该行业违约概率对应的违约距离为-DD;相应地,该行业不违约的概率为1-PD,由标准正态分布累积概率分布函数的性质,有1-PD=1-N(-DD)=N(DD)。因此,该行业非违约概率对应的违约距离为DD。
表9第1行第7~11列表示在第1种违约状态下,5个样本行业违约概率或非违约概率对应的违约距离。由表9第1行第2~6列数据知,在第1种违约状态下,5个样本行业均不违约,故表9第1行第7~11列数据分别为5个样本行业非违约概率对应的违约距离DD i,而5个样本行业非违约概率对应的违约距离DD i来自于表6第1~5行第8列数据。
表9第2行第7~11列表示在第2种违约状态下,5个样本行业违约概率或非违约概率对应的违约距离。由表9第2行第2列数据知,在第2种违约状态下,机械设备业违约,故表9第2行第7列数据为机械设备业违约概率对应的违约距离-DD i,而机械设备业违约概率对应的违约距离来自于表6第1行第8列数据取负号。
由表9第2行第3~6列数据可知,在第2种违约状态下,除机械设备业以外的其余4个样本行业非违约,故表9 第2 行第8~11 列数据分别为该4个样本行业非违约概率对应的违约距离DD i,而该4个样本行业非违约概率对应的违约距离来自于表6第2~5行第8列。
表9其他各行第7~11列数据的含义、来源及其计算过程类推。特别地,在第32种违约状态下,5个样本行业均违约。因此,表9第32行第7~11列数据分别为5个样本行业违约概率对应的违约距离-DD i,而5个样本行业违约概率对应的违约距离来自于表6第1~5行第8列数据取负号。
限于篇幅,表9中仅列出了部分违约状态下各样本行业是否违约对应的违约距离。
3.4.5 基于正态Copula函数的行业违约状态联合概率的计算以表9中第1种违约状态的联合概率JPDs=0.871 709 为例,说明违约状态联合概率JPDs的计算过程。
将表9中5个样本行业的违约距离DD i、表8中5个样本行业违约距离的相关系数矩阵代入式(17),可计算得到第1 种违约状态的联合概率JPDs=0.871 709。
3.5 基于违约状态联合概率的银行信贷资金行业间优化配置模型应用算例
3.5.1 基于信用风险溢价的行业贷款利率的计算表10所示为根据银行贷款基准利率及行业信用风险溢价计算出的行业贷款利率。
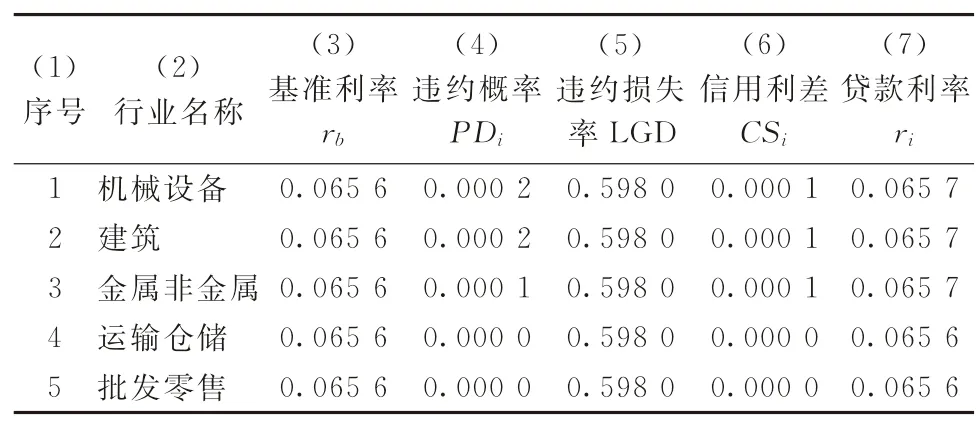
表10 样本行业的贷款利率
表10 第3 列为1 年期银行贷款的基准利率rb=0.065 6[17],数据来自中国人民银行网站。第4列为样本行业的违约概率,数据来自表6第9列。第5列为银行贷款的违约损失率LGD=0.598 0[18],数据来自穆迪公司的技术报告。第6列为行业贷款的信用风险溢价CS i,等于表10第4列的行业违约概率PD i乘以第5列的银行贷款违约损失率LGD。第7列为行业贷款利率ri,等于表10第3列的银行贷款基准利率rb加上第6列的信用利差或信用风险溢价CSi,如式(18)所示。
3.5.2 银行整体信贷资金收益率均值、方差与差异系数的计算表11所示为在各违约状态下,对5个样本行业贷款的收益率或损失率及整体贷款组合的收益率或损失率。
表11第1列为32种违约状态的序号,该序号与表9第1列违约状态的序号相一致。表11第2~6列为各违约状态下,对5个样本行业贷款的收益率或损失率。在贷款到期时如行业不违约,则为收益率,其值等于贷款利率ri;如行业违约,则为损失率,其值等于贷款违约损失率LGD。
表11第1 行第2~6列表示在第1 种违约状态下,5个样本行业贷款的收益率。由表9 第1 行第2~6列数据可知,在第1种违约状态下,5个样本行业均不违约。因此,在第1 种违约状态下,对5个样本行业贷款的收益率即为行业贷款利率ri,即表11第1行第2~6列的数据来自表10第7列。
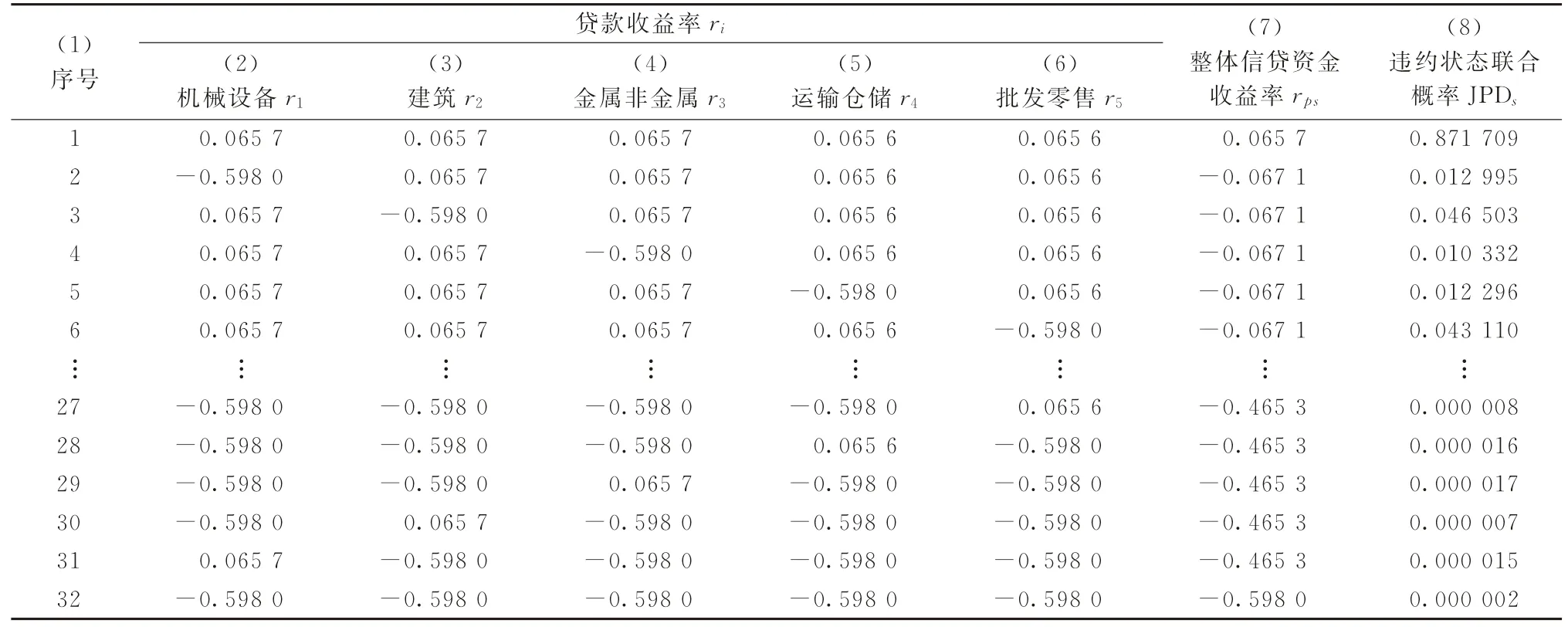
表11 各违约状态下银行整体信贷资金的收益率
表11第2行第2~6列表示在第2种违约状态下,5个样本行业贷款的收益率或损失率。由表9第2行第2~6列数据可知,在第2种违约状态下,机械设备业违约,而其余4个样本行业不违约。因此,在第2种违约状态下,对机械设备业的贷款收益率为-0.598 0,亦即损失率为0.598 0,如表11第2行第2列所示,该数据来自表10第1行第5列。对其余4个样本行业贷款的收益率即为该行业的贷款利率,如表11第2行第3~6列所示,数据分别来自表10第2~5行第7列。
表11其他各行第2~6列数据的含义、来源及其计算过程类推。特别地,在第32种违约状态下,5个样本行业均违约。因此,对5 个样本行业贷款的收益率均为-0.598 0,亦即损失率均为0.598 0,如表11第32 行第2~6 列数据所示,数据来自表10第5列。
限于篇幅,表11中仅列出了部分违约状态下各样本行业贷款的收益率或损失率。
将银行整体信贷资金看作单位1,表11 第7列为在5个样本行业初始贷款权重均为0.200 0的条件下,各违约状态下银行整体信贷资金的收益率。5个样本行业初始贷款权重如表12第3列所示。以表11第1行第7列第1 种违约状态下,银行整体信贷资金收益率=0.065 7 为例,说明各违约状态下银行整体信贷资金收益率rps的计算过程。
将表11第1行第2~6列5个样本行业贷款收益率ri分别乘以对5个样本行业贷款的权重w i,然后相加,可计算得到第1种违约状态下银行整体信贷资金的收益率为
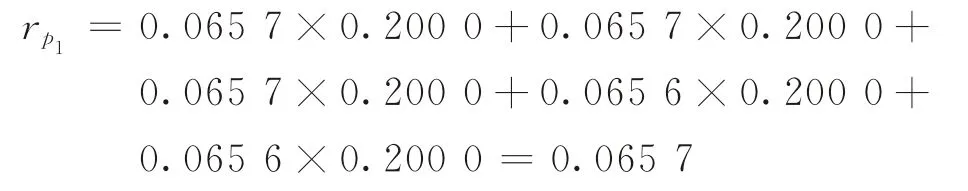
将上述计算结果列于表11第1行第7列。表11第7列其他数据的计算过程类推。表11第8列为各违约状态的联合概率JPDs,数据来自表9 第12列。
表12所示为将银行整体信贷资金看作单位1的情况下,5个样本行业的初始贷款权重与最优贷款权重。
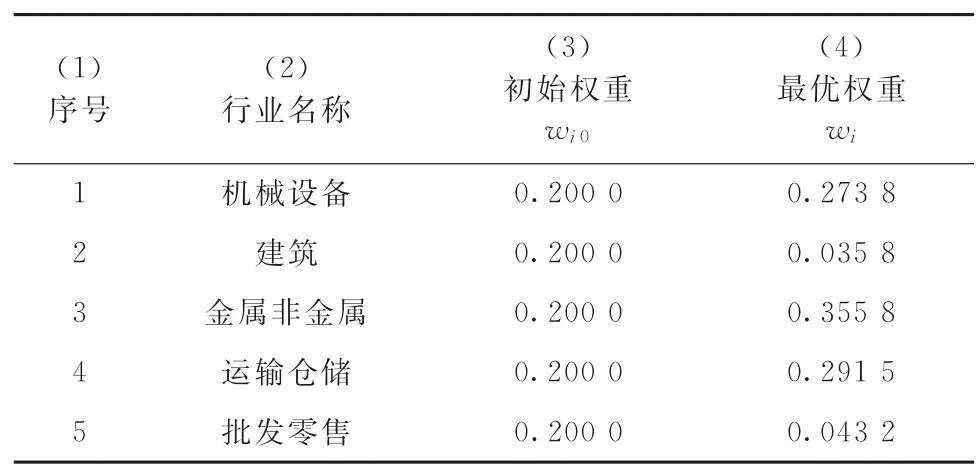
表12 样本行业的初始贷款权重与最优贷款权重
其中,表12 第3 列的初始贷款权重为主观设定,但初始权重的设置并不影响最优贷款权重的求解结果。第4 列的最优贷款权重,通过求解式(24)~(27)得到。
根据各违约状态下银行整体信贷资金的收益率及各违约状态的联合概率,可计算得到银行整体信贷资金收益率的均值、方差及其差异系数,计算结果如表13所示。

表13 银行整体信贷资金收益率均值、方差与差异系数
表13第1行第3列表示在5个样本行业贷款权重均为0.200 0的情况下,银行整体信贷资金收益率的均值。其计算过程为:将表11中各违约状态下的银行整体信贷资金收益率r ps及其联合概率JPDs代入式(20),可计算得到银行整体信贷资金收益率的均值E(rp)=0.045 8。
表13第2行第3列为在5个样本行业贷款权重均为0.200 0的情况下,银行整体信贷资金收益率的标准差。其计算过程为:将表11中各违约状态下的银行整体信贷资金收益率rps及其联合概率JPDs,以及表13中银行整体信贷资金收益率的均值E(rp)代入式(21),可计算得到银行整体信贷资金收益率的方差,对其开平方得到银行整体信贷资金收益率的标准差std(rp)=0.053 8。
表13中第3行第3列为等权重情况下银行整体信贷资金的差异系数θ。其计算过程为:将表13中第2行第3列等权重情况下银行整体信贷资金收益率的标准差std(rp)=0.053 8、第1行第3列等权重情况下银行整体信贷资金收益率的均值E(rp)=0.045 8代入式(23),计算得到等权重情况下银行整体信贷资金的差异系数θ=1.173 5,列于表13第3行第3列。
3.5.3 基于违约状态联合概率的银行信贷资金行业间配置最优贷款权重的计算表12给出了银行信贷资金在行业间优化配置的行业最优贷款权重。为简单起见,设初始权重均为0.200 0,初始权重的设置并不影响最优贷款权重的求解结果。
根据初始贷款权重计算的各违约状态下银行整体信贷资金的收益率r ps列于表11第7列;根据初始贷款权重计算的银行整体信贷资金的期望收益率E(rp)、银行整体信贷资金收益率的标准差std(r p)及银行整体信贷资金的差异系数θ分别列于表13第1~3行第3列。
当贷款权重发生变化时,各违约状态下银行整体信贷资金收益率、银行整体信贷资金收益率的均值和标准差及银行整体信贷资金的差异系数也相应发生变化。
在各样本行业贷款权重之和为1,且贷款权重均大于或等于0的约束条件下,总存在一组贷款权重,使得银行整体信贷资金的差异系数达到最小,即银行整体信贷资金获得单位收益率所承担的风险最小,该组贷款权重即为最优贷款权重。
上述最优贷款权重求解问题实质是一个非线性数学规划问题(见式(24)~(27))。该非线性数学规划问题以银行整体信贷资金中样本行业的贷款权重为决策变量;以银行整体信贷资金的期望收益率大于或等于目标收益率、贷款权重大于或等于0、且贷款权重之和等于1为约束条件;以最小化商业银行整体信贷资金的差异系数θ为目标函数,来确定对各样本行业的最优贷款权重,从而建立银行整体信贷资金行业间最优配置决策方案。
上述数学规划问题可利用Excel软件中的规划求解功能方便地得到对各样本行业的最优贷款权重。
3.5.4 最优权重与等权重下银行整体信贷资金收益率与风险的比较根据各样本行业的最优贷款权重,可重新计算各违约状态下银行整体信贷资金的收益率,从而进一步计算最优贷款权重下银行整体信贷资金收益率的均值和标准差,及最优行业贷款权重下银行整体信贷资金的差异系数。
最优行业贷款权重下银行整体信贷资金收益率的均值E(r p)、标准差std(rp)及最优贷款组合的差异系数θ分别列于表13第1~3行第4列。其计算过程与初始等权重情况下银行整体信贷资金收益率均值、标准差及差异系数的计算过程类似,即与表13第1~3行第3列数据的计算过程类似。
比较表13第1行第3、4列数据可知,初始等权重情况下银行整体信贷资金的平均收益率为0.045 8,而最优行业贷款权重下银行整体信贷资金的平均收益率为0.054 0,最优行业贷款权重下银行整体信贷资金的平均收益率高于初始等权重下银行整体信贷资金的平均收益率。
比较表13第2行第3、4列数据可知,初始等权重情况下银行整体信贷资金收益率的标准差为0.053 8,而最优行业贷款权重下银行整体信贷资金收益率的标准差为0.046 6,最优行业贷款权重下银行整体信贷资金收益率的标准差小于初始等权重下银行整体信贷资金收益率的标准差,亦即最优行业贷款权重下银行整体信贷资金的风险低于初始等权重下银行整体信贷资金的风险。
比较表13第3行第3、4列数据可知,初始等权重情况下银行整体信贷资金的差异系数为1.173 5,而最优行业贷款权重下银行整体信贷资金的差异系数为0.863 3,最优行业贷款权重下银行整体信贷资金的差异系数小于初始等权重下银行整体信贷资金的差异系数,亦即最优行业贷款权重下银行整体信贷资金获得单位收益率所承担的风险小于初始等权重下银行整体信贷资金获得单位收益率所承担的风险。
4 结语
本文以行业内代表性上市公司市值加权的股票价格作为行业平均股价,以市值加权的每股负债作为行业平均每股负债,根据行业平均股价与行业平均每股负债,应用KMV 模型计算行业违约概率,进而将商业银行对m个行业的贷款在到期时区分为2m种违约状态,应用正态Copula函数计算各违约状态的联合概率。根据2m种违约状态下信贷资金的收益率及各违约状态的联合概率,计算银行整体信贷资金的差异系数,即信贷资金获取单位收益所承担的风险。以对m个行业的贷款权重为优化变量,以银行整体信贷资金的差异系数最小化为目标函数,建立了基于违约状态联合概率的商业银行信贷资金行业间优化配置模型,为商业银行信贷资金在行业间的优化配置提供决策参考。

