谈谈水泥生产检验取样代表性问题
胡 洁
(北京国建联信认证中心有限公司,北京 100831)
引 言
水泥生产离不开大量的质量检验活动。质量检验的结果是否反映所检对象的真实质量状况,对于控制水泥质量、稳定生产过程、降低质量成本都具有十分重要的意义。要使质量检验的结果能够反映所检对象的真实质量状况,除了要求检验本身准确无误之外,所检样品的代表性也显得非常重要。如果样品的代表性不好,即使检验结果非常准确也不能反映所检对象的真实质量状况,这样就会误导质量控制,起到适得其反的作用,甚至产生非常严重的后果。从另一方面来看,水泥生产的过程是对大宗物料加工的过程,就一个批次的产品或原料而言,少则几百吨,多则数千吨甚至上万吨。而进行质量检验所需的样品多则只要几千克,少则仅需0.5g。由此可见样品的代表性问题的确不可忽视。怎样对大宗物料进行科学取样,保证样品有足够的代表性,本文就此进行一些分析和研究。
一、相关名词术语
为了分析问题的方便,我们有必要弄清楚相关的几组名词术语的含义。
1.个体与总体
在统计分析中,将研究对象中的每一个最基本的单元称为个体。而将构成研究对象的所有个体的集合即全部个体的总和称为总体(或母体)。总体可以无限大,也可以是有限的,可根据不同的需要进行选择和确定。例如,我们将某个编号的水泥作为研究对象,则这个编号的全部水泥就是总体,而其中的每一包水泥就可以看成是个体。
2.样品及其代表性
按照规定的方法和要求在总体中随机地抽取的一部分个体就称为样品(或样本)。而样品的代表性是指样品能够代表和反映所取样的对象真实质量状况的程度。样品的代表性越好,则它所能代表和反映所取样的对象整体真实质量状况的程度越高。故样品的代表性又可称为样品的可靠性。
3.子样与综合样
在某一空间位置点上和某一时间刻度点上所取得的样统称为子样。前者针对静止堆放的物料取样而言,故又称为点位样;后者则是针对输送或流动中的物料取样而言,故又称为瞬时样。将若干个子样即不同空间位置的点位样或不同时间刻度的瞬时样合并在一起就是综合样(又称混合样)。由此可见,子样所代表和反映的是具体“点”(也可以看成是个体)的状况,而综合样则是代表和反映总体的状况。
4.数据离散性与标准偏差
数据离散性是指一组若干个表示相同意义的数据之间彼此远离(或接近)的程度。在符合正态分布规律的条件下,数据离散性可以用标准偏差值来定量表示。一组离散性数据的标准偏差就是这组数据中的每一个数据与这组数据的平均值之差平方的平均值的算术平方根(参见本文三、1部分)。标准偏差值越大(小),表明数据之间彼此远离的程度越大(小),反之亦然。
二、物料内在质量偏差波动性的本质特征
从相关质量理论和水泥生产实践我们知道,无论是原料、半成品还是成品,内在质量的波动性总是存在的,只是偏差波动的程度不同而已。对于待取样检测的物料而言,整体质量状况是未知的,内在质量的偏差波动程度也是未知的。但是,尽管如此,对于一批确定的物料,无论数量多少,我们都可以视它为若干个检测单元所组成。检测单元就是指进行某项质量指标检测时所需要的最少物料量,它随检测项目的不同而不同。例如,检测熟料f-CaO需要0.5g是试样,则这时的检测单元就是0.5g。那么就可以将某批量的熟料视为由若干个0.5g所组成。从理论上讲我们可以对每一个检测单元分别进行检测,每一个检测单元都可以得到一个检测结果(不考虑检测结果本身存在的偏差,将每个检测结果都视为准确的)。这样就得到若干个检测结果xi(i=1,2,3,……n)。由于物料本身内在质量是不均匀的,所以这若干个检测结果有高有低,也有彼此相等的。任何一个检测单元的检测结果可能是高的或较高的,也可能是低的或较低的,还可能是中等或接近中等的。也就是说它们是在一定范围内随机取值的。若干检测结果的高中低随机性可以用图1直观表示。

图1 所有检测单元检测结果示意图(纵轴表示检测结果,横轴表示所有检测单元)
从图1看,这若干个检测结果虽然看上去杂乱无章,但它们作为一个整体是符合正态分布规律的。即所有检测结果以平均值x-为中心在其两边对称分布。离平均值x-越近的检测结果出现的频率越大,离平均值x-越远的检测结果出现的频率越小,而所有检测结果出现的频率之和为1。最大值与最小值的极差取决于所有检测结果之间的离散程度即标准偏差值的大小(见图2)。正态分布就是物料内在质量偏差波动性的本质特征。
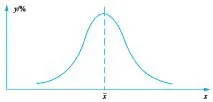
图2 所有检测结果出现的频率曲线图
三、保证取样代表性必须注意的问题
如果物料本身是绝对均匀的,我们只要在这样的物料中的任意位置取足够的样品就可以了。但是由于物料内在质量的偏差波动性总是存在的,所以,为了保证所取样品有足够的代表性,无疑必须采取多点、随机、等量的取样方法进行取样。这是科学取样的基本原则。具体分别论述如下。
1.抽取子样的个数必须足够
通过前面的分析我们得知物料内在质量的偏差波动性符合正态分布规律。而数理统计学知识告诉我们:虽然总体的平均值和标准偏差是无法获知的,但当随机抽取的子样个数足够多时,样品的标准偏差与总体的标准偏差就非常接近,它们之间在数值上差异可以忽略不计,这时就可以以样品的平均值来代表总体的平均值。
我们知道,从总体中抽取有限的n个子样的标准偏差S定义见公式(1)。

而抽取了有限的n个子样后的总体的标准偏差σ可用公式(2)估算(算式的推导本文从略)。

式中:n—所抽取的子样个数;
xi—每一个子样值(i=1,2,3……n);
x-n个子样平均值。
以(1)式除以(2)式得

从(3)式可看出样品标准偏差S与总体标准偏差σ的比值随着抽取子样个数n的增加而接近于1。换句话说也就是随着n的增加样品标准偏差S越来越接近于总体标准偏差σ。笔者选择了一些n的不同取值,分别计算S/σ的值,并列成表1。
从表1可以看出,当n在10~20之间时,样品标准偏差S相对于总体标准偏差σ的误差比较大,大约为2.5%~5.1%,说明抽取子样的个数偏少。而当n>50时,样品标准偏差S相对于总体标准偏差σ的误差很小,只有1%以下。但随着n的再增加,S相对于σ的误差缩小得很缓慢。因此,当n值达到50时再增加子样个数对提高样品的代表性已经没有明显的意义了。显而易见,适宜的、也是足够的子样个数应该在25~50之间。因为在这段区间中样品标准偏差S相对于总体标准偏差σ的误差比较小,只有1%~2%,两者相当接近,完全可以以样品的平均值代表总体的平均值。一般情况下子样个数在25~30个就可以了。对于非常重要的检验取样,比如仲裁检验或者是批量很大的产品或原料可适当增加一些取样点的个数,但最多也没有必要超过50个。
2.子样点的空间位置和时间间隔的要求
子样点的空间位置和时间间隔的要求必须均等地分布在整个取样对象中。
由于物料内在质量是不均匀的,所以,我们在一堆物料中的任一空间位置上所取得的一个点位样的值可能高于总体的平均值;也可能低于总体的平均值;还可能等于总体的平均值。而在物料内部这种高、中、低之间的排列和分布是随机的。也就是说,无论是高值的“样”,中值的“样”,还是低值的“样”都可能分布在这堆物料内部的任何区域,任何空间位置上。这就是物料内在质量差异分布的特性。因此,必须将子样点的位置均等地分布到物料所占据的全部空间。只有这样才能保证取到整个物料中所有不同值的“样”。
同样的道理,对于正在输送过程中的物料,我们也必须以均等的时间间隔在所要取样物料的全部输送过程中抽取瞬时样。不难理解,物料输送的过程可以看成是被输送的物料以若干个“微小部分”分别通过输送设备的过程。在整个输送过程中的任何时刻,通过输送设备的“微小部分”的值出现高、中、低的情形也是随机的。这也是由物料内在质量差异分布的特性所决定的。所以,瞬时样的取样时间间隔也必须均等地分布在所取样物料的整个输送过程中。
实际上,点位样与瞬时样在本质上是一样的,它们都属于子样的范畴,只是在不同情形下的称谓不同而已。点位样是相对于静止堆放的物料取样而言,它突出的是“空间位置点”的概念,取样的时间段则相对固定。而瞬时样是相对于输送或流动中的物料取样而言,它强调的是“时间刻度点”概念,取样的位置则相对固定。点位样与瞬时样之间是可以相互转化的,当我们把对一批静止堆放的物料的取样改为在将这批物料输送入库的过程中取样时,点位样就转化为瞬时样了。反之亦然。
3.每个子样的数量必须相等
由于物料自身内在质量是不均匀的,所以对于一批确定的有限量的物料,我们可以将它看成是由多个不同值的物料以不同的数量所组成。对各个不同值及其所对应的数量进行加权平均计算的结果就是这批物料的平均值。比如,一批数量1 000t熟料,它是由f-CaO含量为5%的熟料100t,f-CaO含量为4%的熟料200t,f-CaO含量为3%的熟料400t,f-CaO含量为2%的熟料200t和f-CaO含量为1%的熟料100t所组成。对各个f-CaO含量及其所对应的数量进行加权平均计算是结果为:(5%×100+4%×200+3%×400+2%×200+1%×100)÷1 000=3%。这就是这批熟料的f-CaO平均值。然而物料中各个不同的值及其所对应的数量是由物料自身决定的,我们事先无法获知。但是,如果整个物料中某个值的数量比较多,那么它被随机抽取到的机会也比较多,反之亦然。所以,我们只要通过抽取足够的子样个数和随机均等的子样位置的方法,就可以抽取到整个物料中所有值的物料,并使代表不同值物料的子样个数所占子样总个数的比例符合整个物料中不同值物料的比例。但是这里需要特别指出的是,在遵循前面两个取样要求的基础上还必须同时注意使取得的每一个子样的数量保持相等。这是因为,如果某些子样的数量与其它子样不相等,就相当于人为地扩大或缩小了不等量子样的值所代表的相应部分物料的“权数”,从而使综合样品的平均值与取样对象的实际情况产生偏差,降低样品的代表性。所以,每个子样的数量必须相等。

表1 n不同取值分别计算S/σ值
四、样品代表性的定量表示
根据表1得知,样品标准偏差S随着抽取子样个数n的增加而接近于总体的标准偏差σ。样品标准偏差S与总体的标准偏差σ越接近,越能够代表总体。所以可以用S与σ比值的百分数来定量表示样品的代表性(可靠性)。例如,当抽取的子样个数为15个时,样品的代表性为96.61%。而当抽取的子样个数为30个时,样品的代表性为98.32%。显而易见,样品的代表性随着抽取的子样个数的增加而提高。但是这里需要特别指出的是,我们在定量表示样品代表性的时候,是以所取得的每个子样的位置和数量都符合要求为前提条件的,否则的话,即使所抽取的子样个数再多其样品也不具有代表性。
五、结 论
1.物料自身内在质量差异分布是随机的,但作为一个整体而言其内在质量的偏差波动性符合正态分布规律。
2.虽然总体的平均值和标准偏差是无法获知的,但当随机抽取的子样个数足够多时,样品的标准偏差与总体的标准偏差非常接近,就可以用样品的平均值来代表总体的平均值。
3.为保证所取样品有足够的代表性,必须做到以下几点:
(1)子样的个数达到足够的数量,一般应达到25个~30个。
(2)所有子样的空间位置点和时间刻度点均等地分布在整个取样对象中。
(3)所取得的每个子样数量相等。
中国建筑材料联合会绿色低碳建材分会
联系人:张晋
电话:13910418604/010-57811107
邮箱:zhangj@cqbm.com.cn
发挥纽带作用 引领建材行业绿色低碳发展
※ 提出促进绿色低碳建材发展的产业技术经济政策,引领行业绿色低碳发展。
※ 制定指标先进的协会团体标准,助力绿色制造体系建设。
※ 把握碳核查、碳交易政策动向,开展建材行业碳交易能力建设。
※ 参与建材低碳产品标准制定及认证工作,推广绿色低碳技术。
※ 参与绿色建材产品评价技术导则制定,促进绿色建材应用。
——勉冲·罗布斯达

