Optimal Model of Continuous Knowledge Transfer in the Big Data Environment

Chuanrong Wu , Evgeniya Zapevalova Yingwu Chen, Deming Zeng and Francis Liu

Abstract: With market competition becoming fiercer, enterprises must update their products by constantly assimilating new big data knowledge and private knowledge to maintain their market shares at different time points in the big data environment.Typically, there is mutual influence between each knowledge transfer if the time interval is not too long. It is necessary to study the problem of continuous knowledge transfer in the big data environment. Based on research on one-time knowledge transfer, a model of continuous knowledge transfer is presented, which can consider the interaction between knowledge transfer and determine the optimal knowledge transfer time at different time points in the big data environment. Simulation experiments were performed by adjusting several parameters. The experimental results verified the model’s validity and facilitated conclusions regarding their practical application values. The experimental results can provide more effective decisions for enterprises that must carry out continuous knowledge transfer in the big data environment.

Keywords: Big data, knowledge transfer, optimization model, simulation experiment,different time points.

1 Introduction

With the market competition becoming fiercer, enterprises must introduce new products based on technological innovation to maintain market share [Chatterjee and Eliashberg(1990)]. This need is more obvious for high-tech enterprises. To achieve technological innovation and launch multi-generation innovative products as well as to improve product performance, enterprises must constantly assimilate new knowledge. The process by which enterprises absorb and innovatively apply knowledge through various channels is termed knowledge transfer [Szulanski (2000)].

The rapid development of the Internet, networking, social networks, and cloud computing has culminated in the big data era. Various types of derivative information have been increasing exponentially. Daily, a flood of data is created by the interactions of billions of individuals using computers, Global Position System (GPS) devices, cellular telephones,and medical devices [Schwab (2012)]. These data are often referred to as ‘big data’,which are characterized by proliferation in the number of data sources and increasing data size. Practical discoveries through aggregation, statistical analysis and the creative combination of data in science, government and private industry indicated the future path of data-driven business [Sukumar and Kerrell (2013)]. Useful knowledge mined from big data by specialized agencies or personnel has become an important type of knowledge from which the individual enterprise can derive strategic advantage [Suchanek and Weikum (2013); Horst and Duboff (2015); Jun, Park and Jang (2015); Manyika, Chui,Brown et al. (2011)]. This type of knowledge can be termed the big data knowledge [Wu,Chen and Li (2016)].

In the big data environment, enterprises must update their products by constantly assimilating new big data knowledge and private knowledge to maintain their market shares at different time points. Big data knowledge can enhance productivity and create significant value for enterprises by guiding decisions, trimming cost and increasing the quality of products and services [McGuire, Manyika and Chui (2012); Lohr (2012)].Private knowledge is usually the core patent knowledge, which sometimes cannot be obtained from big data, or mining from big data may involve violations of intellectual property rights and personal privacy [Wu, Zhu and Wu (2014)]. Typically, the two types of knowledge are not transferred simultaneously.

Scholars have studied the importance of knowledge transfer in the big data environment[Wu, Chen and Li (2016); Koman and Kundrikova (2016); Wu (2017)]. Several studies suggest that enterprises must transfer at least two types of knowledge in the big data environment. However, these studies only analyzed the simultaneous occurrence of two types of knowledge [Wu, Chen and Li (2016); Wu (2017); Wu, Zapevalova, Chen et al.(2018)]. There is no literature on continuous knowledge transfer in the big data environment. Although Wu et al [Wu, Zapevalova, Chen et al. (2018)] have studied multiple knowledge transfer in the big data environment, they just take the knowledge transfer at different time points as many times of independent knowledge transfer.However, the first knowledge transfer usually affects the second knowledge transfer in real-world circumstances if the time interval is not too long. It is necessary to study the problem of continuous knowledge transfer in the big data environment.

A number of scholars have analyzed multi-generation product or technology knowledge diffusion using Bass or Lotka-Voherra models [Kim, Shin, Park et al. (2009); Barkoczi,Lobonţiu and Bacali (2015); Ganguly (2015)]. These models are primarily concerned with technical knowledge diffusion in the entire market and scarcely address the change in continuous knowledge transfer efficiency of each enterprise. Some scholars suggest that artificial neural network (ANN) learning model be applied for user recommendation and prediction from the big data [Jung, Kim and Sim (2016)]. Although ANN modeling procedure consists of learning, validation and prediction steps, the efficiency of knowledge transfer is seldom considered. Some scholars believe that the selection of the optimal time is one of the most important factors to improve the efficiency of knowledge transfer [Farzin (1996); Doraszelski (2004); Wu and Zeng (2009); Szulanski, Ringov and Jensen (2016); Wu, Chen and Li (2016); Liu, Zhang and Xia (2017); Shinde and Ashtankar (2017); Wu, Zapevalova, Chen et al. (2018)].

This paper proposes a time optimization model for continuous knowledge transfer. This model can consider the interaction between each knowledge transfer and determine the optimal knowledge transfer time at different time points in the big data environment. The experimental results can provide more effective decisions for enterprises that must carry out continuous knowledge transfer in the big data environment. In the first section, the importance of continuous knowledge transfer in the big data environment and the necessity of analyzing continuous knowledge transfers are considered. Model hypotheses and the modeling method are presented in Section 2. A time optimization model of continuous knowledge transfer is presented in Section 3. The simulation experiments and the analysis of the model results are described in Section 4. Conclusions are drawn in Section 5.

2 Hypotheses and modeling method

Assume that an enterprise must transfer only two types of knowledge in the big data environment. One type of knowledge is big data knowledge provided by a big data knowledge provider. The other type is private knowledge provided by another enterprise.The two types of knowledge are not transferred simultaneously. Rather, the private knowledge is transferred soon after the big data knowledge.

2.1 Quantitative expression of knowledge transfer in the big data environment

An innovation network is a social context of enterprises and research institutes that are linked to one another to share resources and knowledge to gain critical competencies that contribute to their competitiveness in the marketplace [Zuech, Khoshgoftaar and Wald(2015)]. In the big data environment, knowledge resources associate with one another through the Internet. The scale of the innovation network becomes large, the connections between the knowledge storage units are complex, and the knowledge storage units have heterogeneity. Enterprises in innovation networks can directly share resources and knowledge with one another. In addition, they can obtain knowledge of other knowledge storage units from big data knowledge providers. It is difficult to fully characterize an innovation network in the big data environment using a general binary network.

2.2 Model hypotheses

This paper is based on previous research on one-time knowledge transfer. The same assumptions and variables remain unchanged as follows: the total ma rket volume of the product is, the price of the product is, the discount rate is , the marginal cost in the starting period is, the absorption capacity is, the market share ofin the starting period is, and the life cycle of the product is. For details on assumptions, see models of Wu et al. [Wu, Chen and Li (2016); Wu and Zeng(2009)]. In addition, eight new hypotheses are proposed:

Hypothesis 1.andare two enterprises in,is a big data knowledge provider in, andproduces only one product.

Hypothesis 2.transfers one type of big data knowledge fromfirstly at time period. After time period,transfers the private knowledge from

Hypothesis 3.The market share ofincreases at a rate ofin the firstperiods and decreases at a rate ofin other periods.

Hypothesis 4.is the growth rate of the market share ofin the firstperiods immediately aftertransfers big data knowledge at the time period.is the growth rate of the market share ofin the firstperiods immediately aftertransfers the private knowledge at time period.

Hypothesis 5.The update rate of the big data knowledge at time periodis,and the update rate of private knowledge at the time periodis.

Hypothesis 6.is the discount expectation of profits (DEP) ofreceived before transferring the big data knowledge,is the DEP ofreceived after transferring the big dataknowledge and before transferring the private knowledge, and is the DEP of received after transferring the private knowledge at time period.

Hypothesis7.is the knowledge transfer cost of the big data knowledge,is the knowledge transfer cost of the private knowledge.

Hypothesis 8.The life cycle of productis renumbered after each knowledge transfer.

2.3 Conceptual model of continuous knowledge transfer

Based on Hypotheses 2, 6 and 7,wants to transfer one type of big data knowledge at time periodand one type of private knowledge at time period.is the DEP ofreceived before transferring the big data knowledge,is the DEP ofreceived after transferring the big data knowledge, andis the DEP ofreceived after transferring the private knowledge.is the knowledge transfer cost of the big data knowledge, andis the knowledge transfer cost of the private knowledge. The total DEP ofcan be denoted as. Therefore,The conceptual model is as shown in Fig. 1.

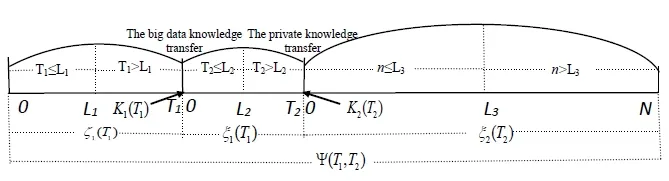
Figure 1: Conceptual model of continuous knowledge transfer

3 Optimization model of continuous knowledge transfer

3.1 DEP before the big data knowledge transfer

Because no new knowledge transfer occurs during this period, the enterprise produces new productsusing prior knowledge. The market share changes from growth to decay in time period . Thus, the entire life cycle can be divided into two phases. The net profit of the enterprise can be calculated by subtracting the total cost from the total sales revenue. Then, the total DEP before knowledge transfer can be obtained by discounting the profit of each phase to the starting pointThe DEP before knowledge transfer is shown as Eq. (1). The detailed calculation is introduced by Wu et al. [Wu and Zeng(2009)].

3.2 Transfer cost of the big data knowledge

The cost of knowledge transfer consists of fixed cost and variable cost. In the big data environment, enterprises must pay a fixed data-processing fee when transferring big data knowledge from the big data knowledge provider. Thus, the fixed transfer cost of the

The variable cost is related to the potential difference between the external knowledge and the internal knowledge. The enterprise accumulates its knowledge stock according to the knowledge absorption capacity , and the internal knowledge in time periodis. The update rate of external big data knowledge in time periodis. Therefore, the knowledge potential difference can be expressed as. The variable cost can be computed by, whereis a constant. By discounting the transfer cost to the starting point after adding the fixed cost and variable cost, the present value of the big data knowledge transfer cost in the big data environment can be expressed as Eq. (2).

3.3 DEP after the big data knowledge transfer

From Hypotheses 3 and 4, the market share ofincreases at the rate ofin the firstperiods immediately aftertransfers the big data knowledge at time period. Then, it decays at a rate of. Therefore, the market share ofin periodafter the big data knowledge transfer can be denoted as in Eq. (3).

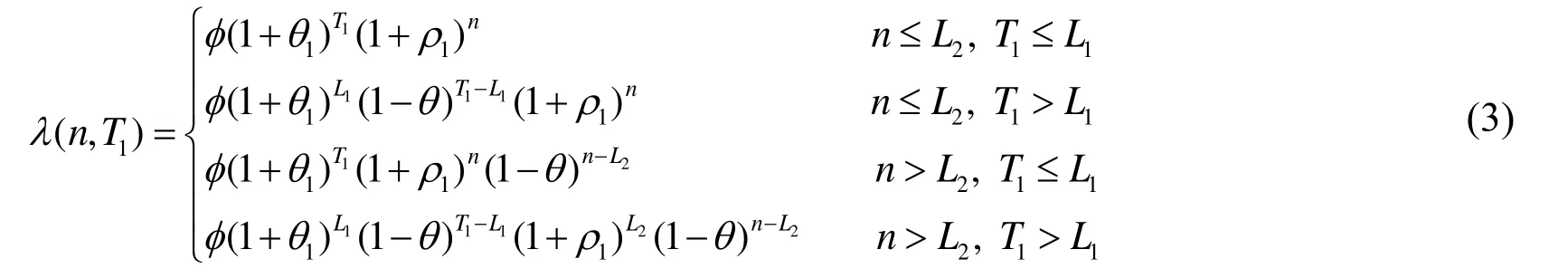
If we discount the profits in periodto the starting point by multiplying Eq. (4) byand sum up all the discount profits in period, the DEP after the big data knowledge transfer and before the private knowledge transfer is as in Eq. (5).

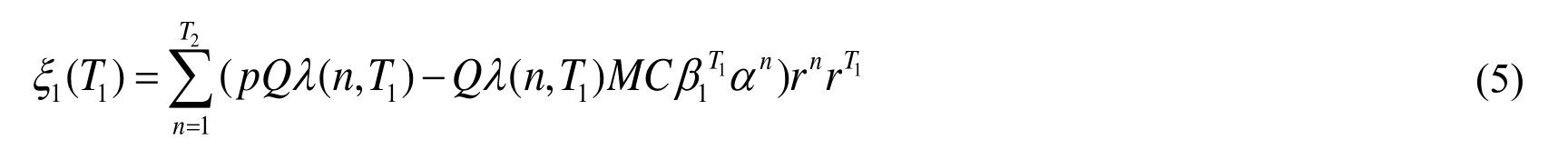
When transferring big data knowledge from a big data knowledge provider, the enterprise often finds that certain core patent knowledge cannot be acquired. Thus, the enterprise transfers private knowledge from another enterprise or research institute. Typically, the time between the big data knowledge transfer and the private knowledge transfer is not long. Therefore, we assume that the private knowledge transfer occurs during the growth stage of the market share, as presented in Hypothesis 4: . Based on Eqs. (3) and(5), the expected profits after the big data knowledge transfer and before the private knowledge transfer can be expressed as Eq. (6).

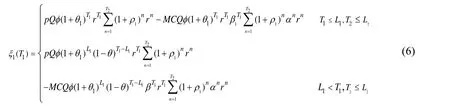
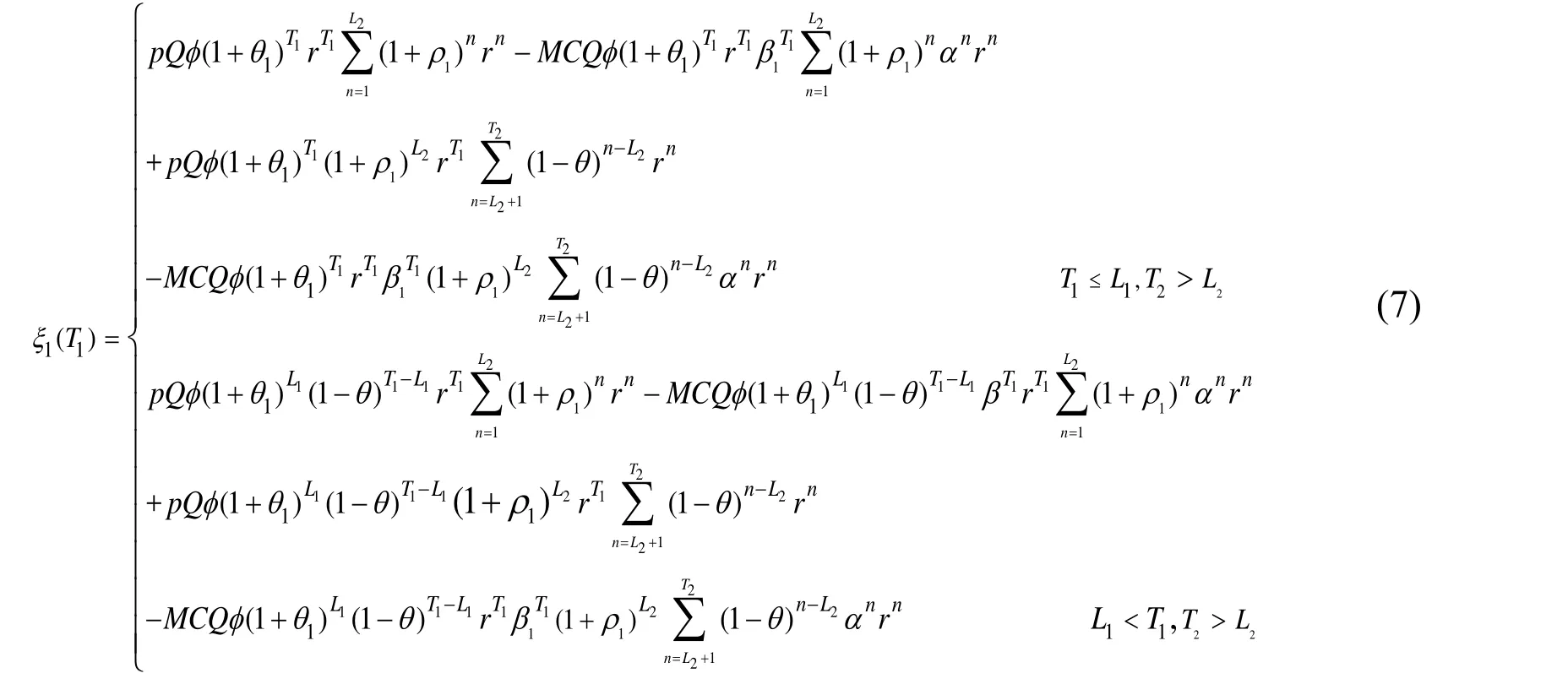
3.4 Transfer cost of the private knowledge

The private knowledge is the core patent knowledge. Therefore,must pay a portion of the patent license fee as the fixed cost of the private knowledge when transferring such knowledge. Suppose is the fixed transfer cost of the private knowledge, which is a constant.After time period,accumulates knowledge stock based on the efficiency of the big data knowledge. The knowledge absorption capacity is, and the internal knowledge in time periodis. The update rate of external private knowledge in time periodis. Therefore, the knowledge potential difference can be expressed as. The variable cost can be computed byis a constant. By discounting the transfer cost to the starting point after adding the fixed cost and variable cost, the present value of the private knowledge transfer cost can be expressed as Eq. (8).

3.5 DEP after the private knowledge transfer

From Hypotheses 3 and 4, the market share ofincreases at the rate ofin the firstperiods immediately aftertransfers the private knowledge at time period.Subsequently, it decays at a rate of. Therefore, the market share ofin periodafter the transfer of private knowledge at the time periodcan be denoted as in Eq. (9).

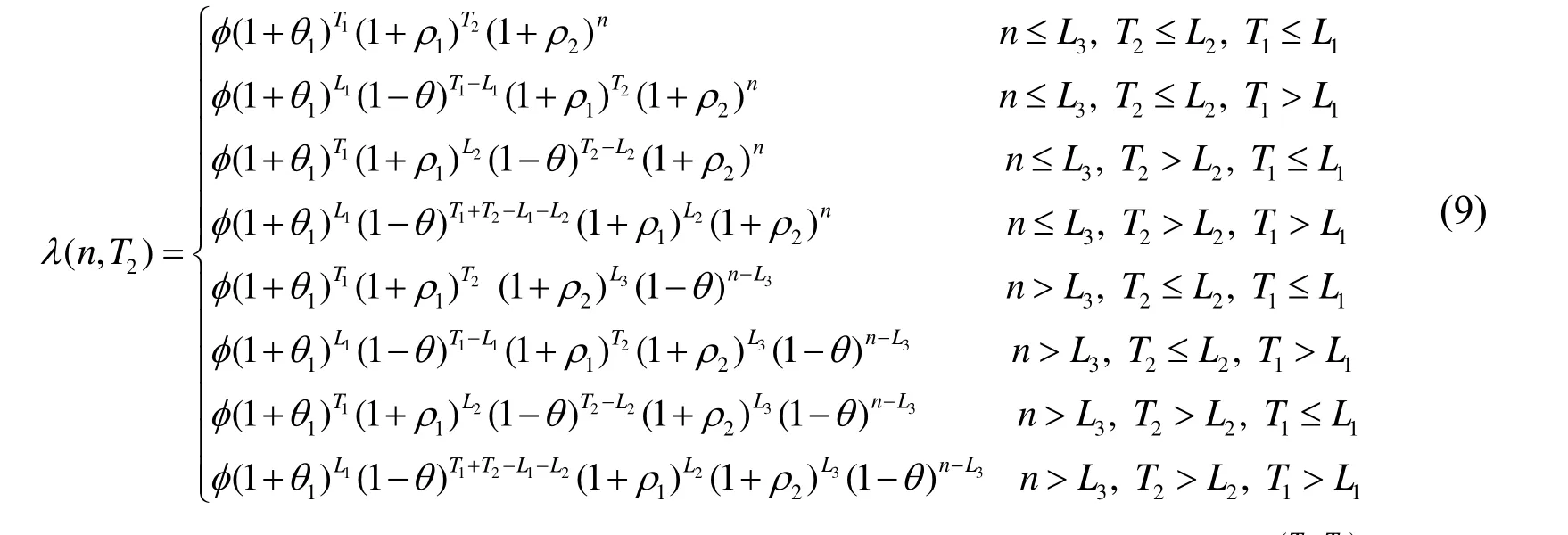
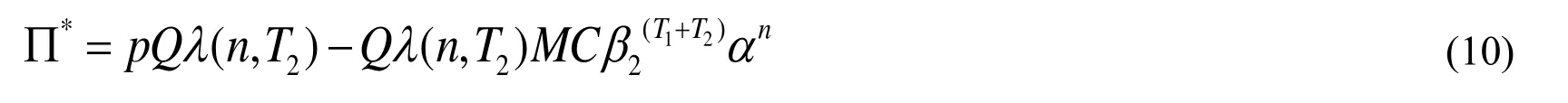
We discount the profits in periodto the starting point by multiplying Eq. (10) byand sum all the discount profits in period. Thus, the DEP after the private knowledge transfer is as in Eq. (11).

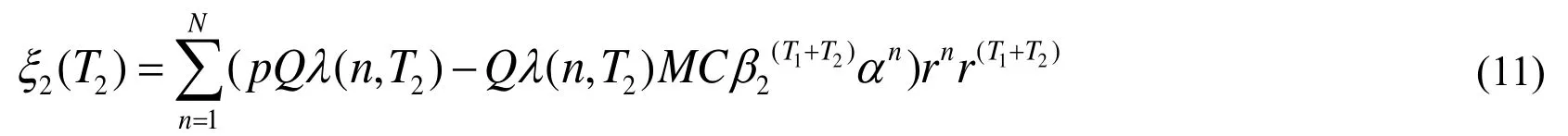
Based on Eqs. (9) and (11), the expected profits after the private knowledge transfer can be expressed as Eqs. (12) and (13).

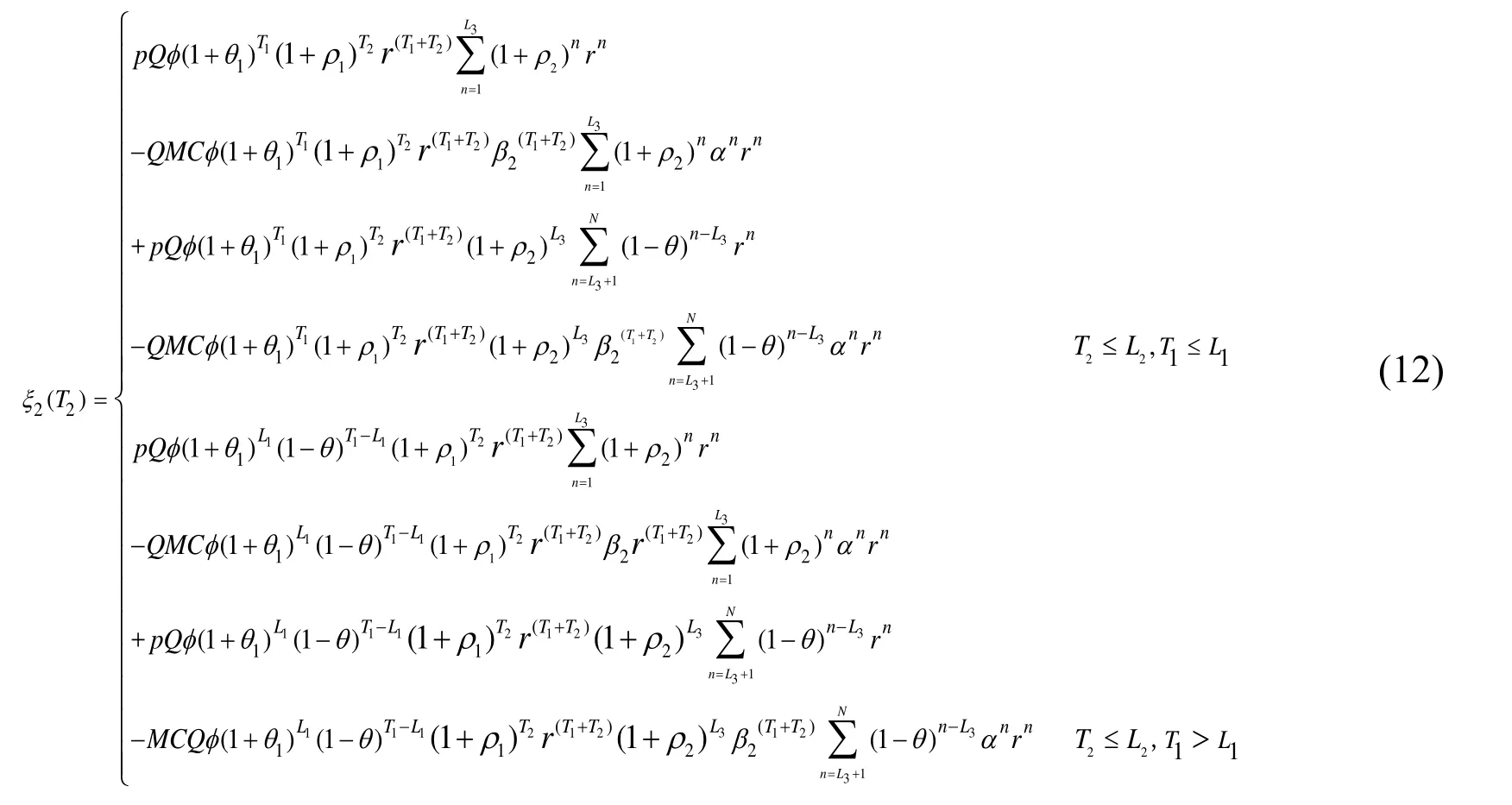
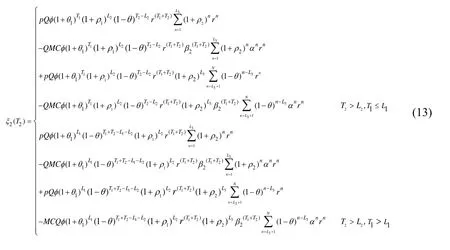
3.6 Total DEP model of continuous knowledge transfer

The optimization problem of two-times knowledge transfer at different time points is to find the maximum offor the given parameters. Therefore, the optimization model of knowledge transfer can be expressed as Eq. (14).

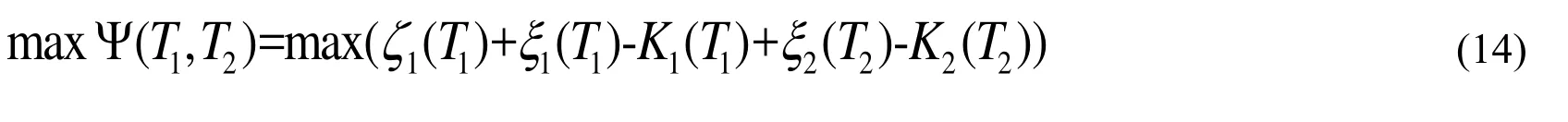
4 Simulation and results of continuous knowledge transfer

4.1 Model solution

4.2 Simulation experiments

(1) Parameter setting and simulation. To simulate the actual situation of knowledge transfer in the big data environment, several parameters are chosen for testing. The values of the parameters used by Wu et al. [Wu, Chen and Li (2016)] are presented in Tab. 1.

Table 1: Parameter values

The values of several new parameters are presented in Tab. 2.

Table 2: Parameter values

Table 3: Total DEP with T1 and T2

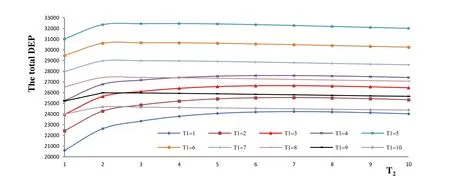
Figure 2: Changes in total DEP with T1 and T2

To determine the influence degree of the knowledge absorption capacityon the DEP and the optimal time of knowledge transfer in the big data environment, all the parameters exceptare set with the same values as in section (1). Changingfrom 95% to 90% means that the knowledge absorption capacity is enhanced. Tab. 4 and Fig. 3 show the DEP varying with . From the experimental results in Tab. 4 and Fig. 3,the optimal knowledge transfer time of the big data knowledgeremains 5. However,the optimal knowledge transfer time of the private knowledgechanges from 4 to 3.Therefore, when the knowledge absorption capacity increases, the optimal knowledge transfer time of big data knowledge remains the same. However, the optimal knowledge transfer time of private knowledgewill be earlier. The reason is that the big data knowledge is precisely like common knowledge. The knowledge absorptive capacity has little effect on the optimal knowledge transfer time of the big data knowledge. However, the optimal knowledge transfer time of the private knowledge transfer is advanced.

Table 4: Total DEP with

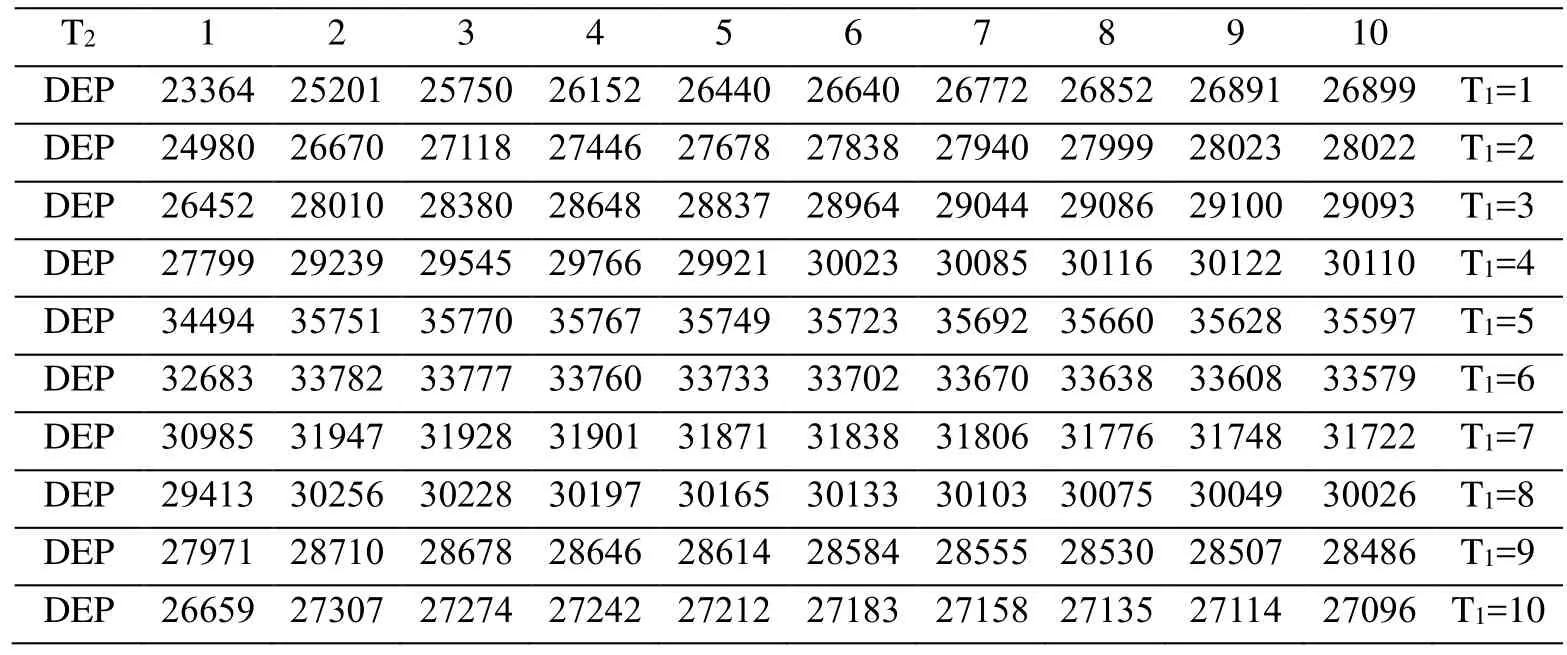
Table 4: Total DEP with

T2 1 2 3 4 5 6 7 8 9 10 DEP 23364 25201 25750 26152 26440 26640 26772 26852 26891 26899 T1=1 DEP 24980 26670 27118 27446 27678 27838 27940 27999 28023 28022 T1=2 DEP 26452 28010 28380 28648 28837 28964 29044 29086 29100 29093 T1=3 DEP 27799 29239 29545 29766 29921 30023 30085 30116 30122 30110 T1=4 DEP 34494 35751 35770 35767 35749 35723 35692 35660 35628 35597 T1=5 DEP 32683 33782 33777 33760 33733 33702 33670 33638 33608 33579 T1=6 DEP 30985 31947 31928 31901 31871 31838 31806 31776 31748 31722 T1=7 DEP 29413 30256 30228 30197 30165 30133 30103 30075 30049 30026 T1=8 DEP 27971 28710 28678 28646 28614 28584 28555 28530 28507 28486 T1=9 DEP 26659 27307 27274 27242 27212 27183 27158 27135 27114 27096 T1=10

Figure 3: Changes in total DEP with

Table 5: Total DEP with

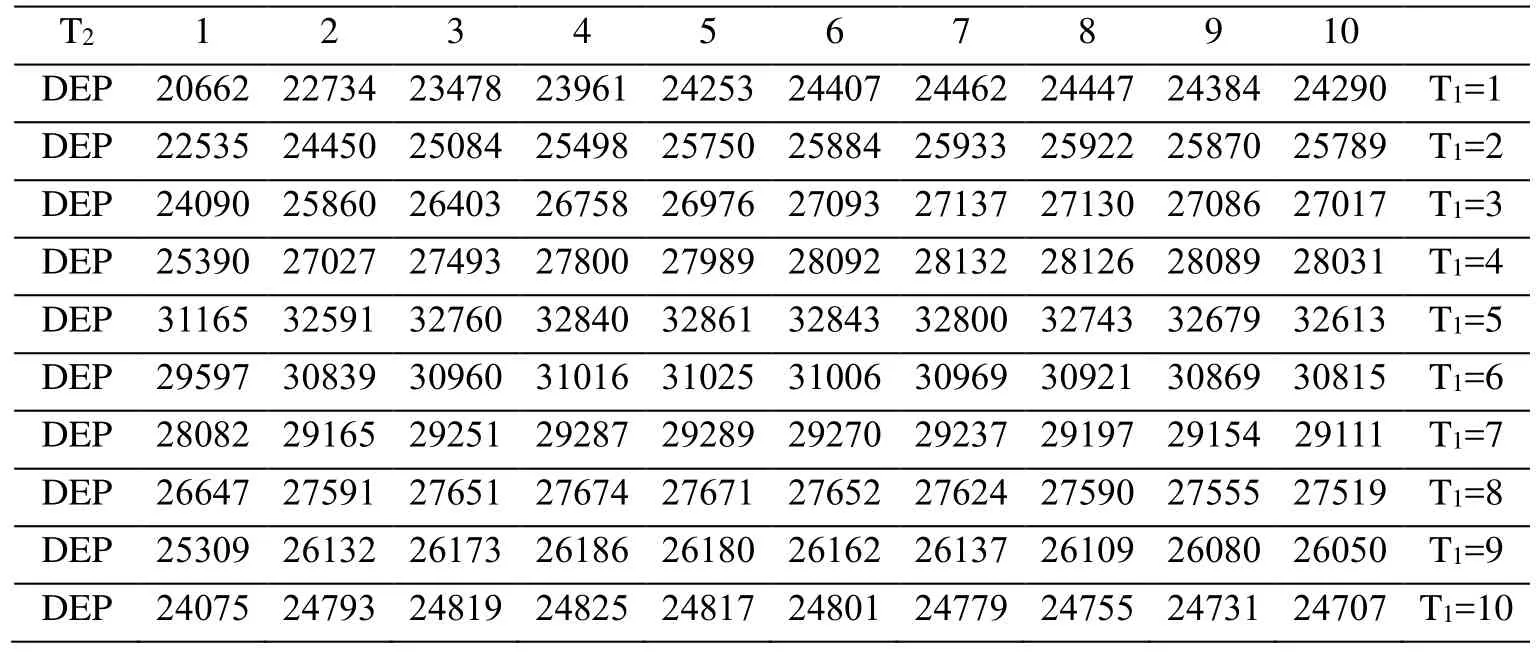
Table 5: Total DEP with

T2 1 2 3 4 5 6 7 8 9 10 DEP 20662 22734 23478 23961 24253 24407 24462 24447 24384 24290 T1=1 DEP 22535 24450 25084 25498 25750 25884 25933 25922 25870 25789 T1=2 DEP 24090 25860 26403 26758 26976 27093 27137 27130 27086 27017 T1=3 DEP 25390 27027 27493 27800 27989 28092 28132 28126 28089 28031 T1=4 DEP 31165 32591 32760 32840 32861 32843 32800 32743 32679 32613 T1=5 DEP 29597 30839 30960 31016 31025 31006 30969 30921 30869 30815 T1=6 DEP 28082 29165 29251 29287 29289 29270 29237 29197 29154 29111 T1=7 DEP 26647 27591 27651 27674 27671 27652 27624 27590 27555 27519 T1=8 DEP 25309 26132 26173 26186 26180 26162 26137 26109 26080 26050 T1=9 DEP 24075 24793 24819 24825 24817 24801 24779 24755 24731 24707 T1=10

Figure 4: Changes in total DEP with

Table 6: Total DEP with

Table 6: Total DEP with

T2 1 2 3 4 5 6 7 8 9 10 DEP 21627 23870 24594 24984 25146 25156 25068 24917 24732 24528 T1=1 DEP 23662 25597 26104 26357 26438 26405 26298 26146 25970 25783 T1=2 DEP 25273 26963 27314 27471 27498 27438 27324 27177 27013 26843 T1=3 DEP 26559 28054 28293 28384 28376 28302 28188 28050 27900 27746 T1=4 DEP 32206 33466 33396 33261 33093 32912 32730 32557 32397 32251 T1=5 DEP 30500 31571 31469 31328 31170 31007 30850 30702 30567 30446 T1=6 DEP 28849 29769 29653 29516 29372 29229 29094 28969 28856 28756 T1=7 DEP 27290 28084 27967 27839 27710 27586 27471 27366 27273 27190 T1=8 DEP 25840 26530 26418 26302 26189 26083 25986 25899 25821 25752 T1=9 DEP 24509 25112 25008 24905 24808 24718 24636 24563 24499 24442 T1=10

Figure 5: Changes in total DEP with

To determine the influence of the parameters on the optimal knowledge transfertime of the big data knowledge transfer, several parameters, such as,, and , are adjusted separately. However, the optimalknowledge transfer time of the big data knowledge remains unchanged. Only when is adjusted from 4 to 3 does, the optimal knowledge transfer time of big data knowledgechange from 5 to 4 (Fig. 6). This outcome means that when the market share knowledge begins to decrease, enterprisetransfers the big data knowledge from the big data knowledge provider.

Figure 6: Changes in total DEP with

Based on the experim?ental results in Fig. 2 and 7, the optimal knowledge transfer time of private knowledge changes from 4 to 2. This outcome implies that if the market share of the private knowledge becomes larger after knowledge transfer, the optimal knowledge transfer time of the private knowledge advances. The reason for enterpriseto adopt the private knowledge earlier is that the core patent knowledge can help enterprise obtain a larger market share. Therefore, the simulation results of the model are consistent with the practical situation.

5 Conclusion

This paper analyzed the time optimization problem of continuous knowledge transfer of two types of knowledge in the big data environment. Based on an analysis of the importance of continuous knowledge transfer in the big data environment and the mutual influence of each knowledge transfer, a time optimization model of continuous knowledge transfer was established. Several simulation experiments were performed on typical parameters. The experimental results verified the model’s validity and facilitated conclusions regarding their practical application values. The experimental results can provide more effective decisions for enterprises that must carry out continuous knowledge transfer in the big data environment.

Acknowledgments: This research was supported by the National Natural Science Foundation of China (Grant No. 71704016, 71331008), the Natural Science Foundation of Hunan Province (Grant No. 2017JJ2267), Key Projects of Chinese Ministry of Education (17JZD022); and the Project of China Scholarship Council for Overseas Studies (201208430233, 201508430121), which are acknowledged.