Mass Transfer of MHD Nanofluid in Presence of Chemical Reaction on A Permeable Rotating Disk with Convective Boundaries, Using Buongiorno’s Model

Muhammad Shoaib Arif *, Yasir Nawaz Mairaj Bibi and Zafar Ali

Abstract: This communiqué is opted to study the flow of nanofluid because of heated disk rotation subjected to the convective boundaries with chemical reaction of first order.Wherein Buongiorno’s model for nanofluids is used due to its wide range of applications and the rotating disk under investigation is permeable. Small magneto Reynolds parameter and boundary layer assumptions are carried out to formulate the problem. The system of nonlinear partial differential equations governing the flow problem is converted into the set of ordinary differential equations by using particular relations known as Von Karman transformations. The complicated set of coupled ordinary differential equations with complicated boundary conditions is set to solve by an analytical technique Homotopy Analysis Method (HAM). Whereby the results obtained by the aforementioned method are provided analytically and analyzed graphically. Also validation of the work is confirmed by providing comparison of previous works in tabular form. Effect of chemical reaction parameter on mass transfer rate is also highlighted tabularly for its increament. Nusselt and Sherwood numbers calculated and compared to the like literature and found in good agreement.

Keywords: Chemical reaction, rotating disk, nanoparticles, velocity slip, magnetic effect.

Nomenclature

1 Introduction

The motion because of a disk rotation is the subject matter of current study because of extensive variety of programs in aerospace technology and engineering science such as equipments of rotation, systems of medical science, heat energy producing structure gasoline turbines, computer storage gadgets, rotor-stator systems, method of crystal rooming, machines of cleansing air and lots of others. Karman [Karman (1921)] is reported as the first who initially solved this type of problem wherein he evolved the well-known similarity relations in order to switch a set of PDEs into ODEs system. Many researchers around the globe have shown their interest and evaluation in this type of work under their unique approaches. Combined effect of mass and heat transportation in viscous flow, because of porous and rotating disk is discussed and reported numerically by Turkyilmazoglu et al. [Turkyilmazoglu and Senel (2013)]. In Rashidi et al. [Rashidi,Kavyani and Abelman (2014)] analyzed entropy production effect on the viscous flow of disk rotation. Again Nanofluid flow effects of disk rotation are mentioned and analyzed by Turkyilmazoglu [Turkyilmazoglu (2014)]. Viscous Nano fluid flow produced with the aid of disk rotation and its contraction is studied in Hatami et al. [Hatami, Sheikholeslami and Ganji (2014)] wherein a technique of least rectangular is utilized. Nanofluid flow because of inclined disk rotation and disk linear stretching is tested and supplied in Mustafa et al. [Mustafa, Khan, Hayat et al. (2015); Sheikholeslami, Hatami and Ganji(2015)], respectively. Also, Sheikholeslami et al. [Sheikholeslami, Rashidi, Hayat et al.(2016)] numerically investigated the effect of radiation on the components of velocity and temperature profile through rotating disk in porous regime.

Commercial production methods call for upright rates of heat transfer. The traditional and ongoing methods are failed to offer perfect and higher rates of it to meet the needs of industries. Therefore enhancing its rates is the chief manifesto of researchers of this age.Normally, enhancing strategy may be labeled in two classes, specifically active and passive ones. Former requests for unique geometry, component of fluids and thermal filling and so forth. While later urges for outside effects of force including electric and magnetic fields. The idea by the back of adding particles into fluid is to increase the overall functioning of regular fluids [Maxwell (1873)] so many researchers have attempted to study the effects of Nanofluidic mixtures with high heat transport developments. Various effects like congestion of scrape, loss of extra pressure and all these are discussed making this type of fluid mixture irrespective of higher heat transfer.Choi [Choi (1995)] for the first time brought a brand new beauty into Nano-science namely Nanofluids. He exposed after experiments that liquids carrying Nanofluids beautify thermo performances efficiently. In the form of Buongiorno model of nanoparticles,[Buongiorno (2006)] introduced Brownian and thermophoretic factors in this fluid. The current improvements in nanofluids may be observed within Imen et al. [Imen, Ahmed,Mohammed et al. (2014); Shamashuddin and Satya Narayana (2018); Neffahl, Kahalerras and Fersadou (2018); Neffahl, Kahalerras and Fersadou (2018).

The significance of Nanoliquids with magneto properties has been improved significantly in biomedical corporations. Fluids of this type have many applications in drugs such as sensible wound remedial bio-materials and so forth. Magnetic fields may be taken in to consideration for manufacturing Nanoliquids conducting electrically in order to acquire products of high quality in commercial production. Exceptional considerations have been given to study the overall working of Nanofluids mixtures wherein the small size particles are identical to that of DNA or protein orders. Nanoparticles with magneto properties are also applied to bronchial asthma remedy, targeting drug release, magnetic resonance imaging, synergistic results in immunology, removal of tumour through hyperthermia, etc. [Hayat, Waqas, Khan et al. (2016)]. In Uddin et al. [Uddin, Beg and Amin (2014)], temperature base fluid flows on fine and thin films are studied for magnetic field effectiveness. Sheikholeslami et al. [Sheikholeslami, Ganji, Javed et al.(2015); Sheikholeslami, Rashidi, Hayat et al. (2016); Sheikholeslami, Hatami and Ganji(2015)] studied nanofluid viscosity depending upon magnetic field in Lin et al. [Lin and Zheng (2015)]. Magnet effects on the flow field of nanofluid Maxwell model stratified solutally and thermally in Sheikholeslami et al. [Sheikholeslami, Ganji, Javed et al.(2015)]. MHD effects are suggested through Sisko nanofluid by Abbasi et al. [Abbasi,Shehzad, Hayat et al. (2016)] where in surface is stretched bidirectionally. Abbasi et al.[Abbasi, Shehzad, Hayat et al. (2016)] studied 3D MHD flow, stratification of thixotropic and Oldroyd-B nanofluid models.

In view of Hayat et al. [Hayat, Malvandi, Shehzad et al. (2016, 2017)] Chemical reaction have numerous industrial applications which include meals production, atomic reactors,transportation of energy below earth, magneto plasmas flow manufacturing of polymer,making of ceramic and better petroleum restoration. Chemical species inside the nanofluid mixture creates transfer of mass only if there happens concentration. Chemical reaction may be of any orderprovided that reaction rate proportionate the concentration raised power. Chemical reaction having first order reaction is the best among all.Universally 2ndand 3rdorder chemical reactions are treated to be unfavourable. This article is subjected to figure out impact of MHD flow of viscous Nano fluid and effect of chemical reaction to the species transportation because of the disk rotation accompanying magnetic field. Process like thermophoresis and Brownian motion occurs because of nanospecies under consideration. The PDEs of the steady viscous motion, temperature and concentration are renewed in to the set of ODEs through Von Karman transformations and hence solved by HAM. Sherwood and Nusselt parameters are provided for one and all type dimensional parameters.

2 Mathematical formulation

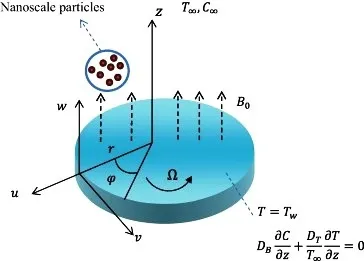
Figure 1: Geometry of the flow problem

Consider an infinite permeable rotating disk, as shown in Fig. 1, that rotates aboutz-axis with angular velocityand fluid mixture be:

• Steady

• Incompressible

• Electrically conducting

• Chemically reacting

The governing equations of the axisymmetric flow in cylindrical coordinate system, using Buongiorno’s model, are:

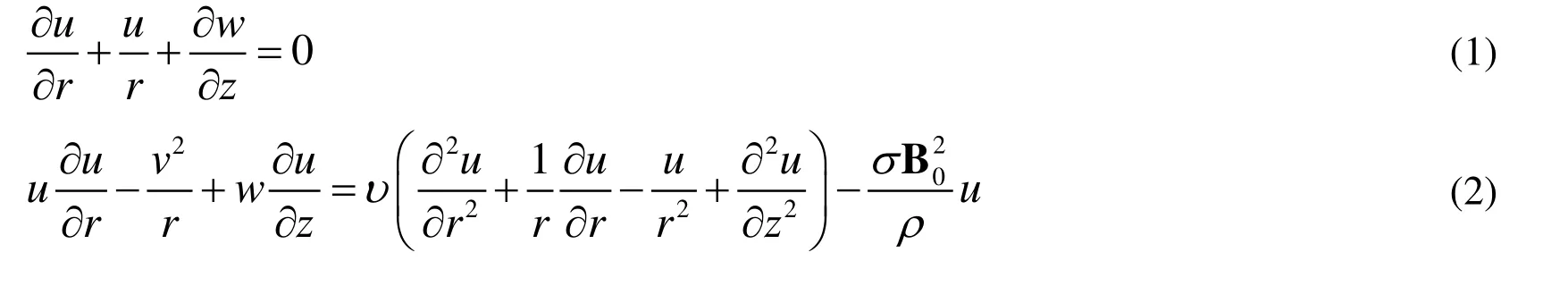
Subjected to the boundary conditions

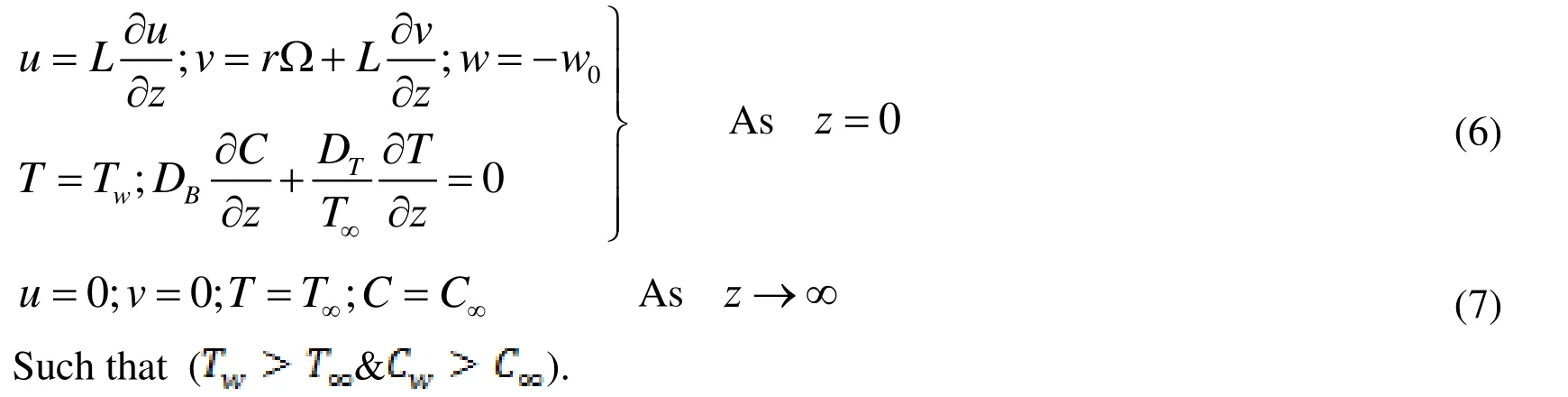
Introducing the V. K relations [Pandey and Kumar (2017)];

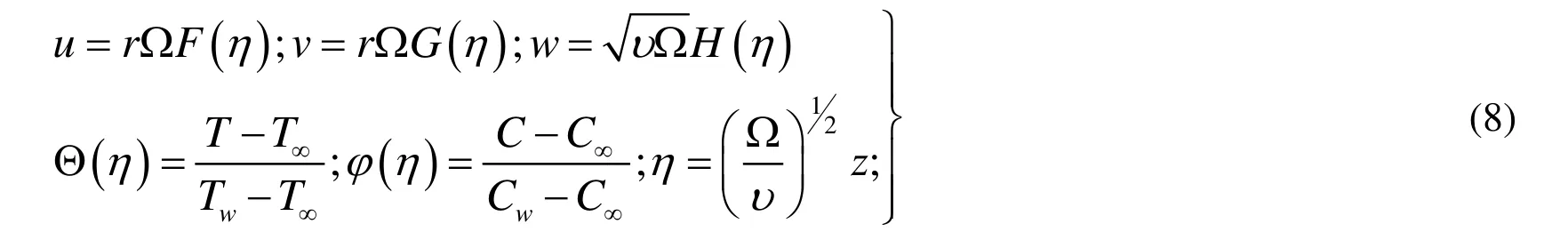
Eqs. (1)-(6) are then converted to the set of ODEs

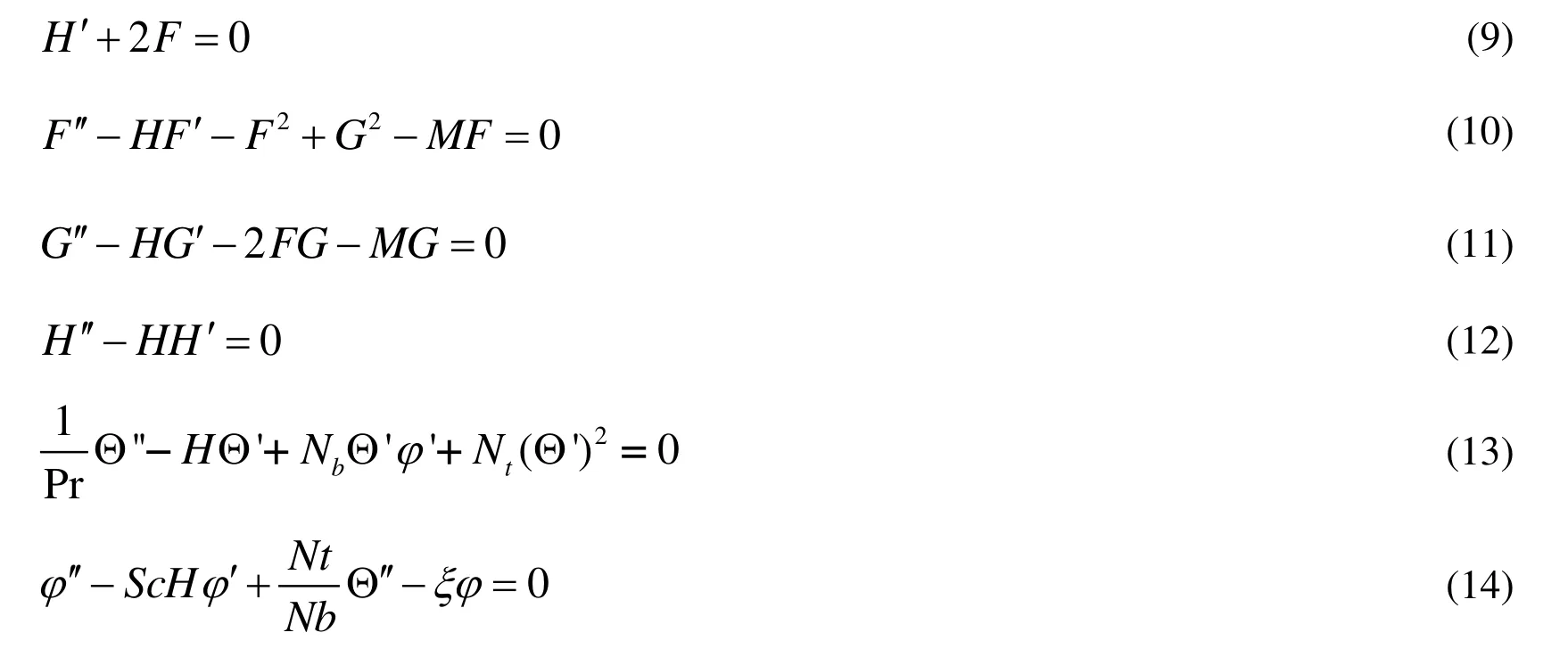
Associated boundary conditions are;

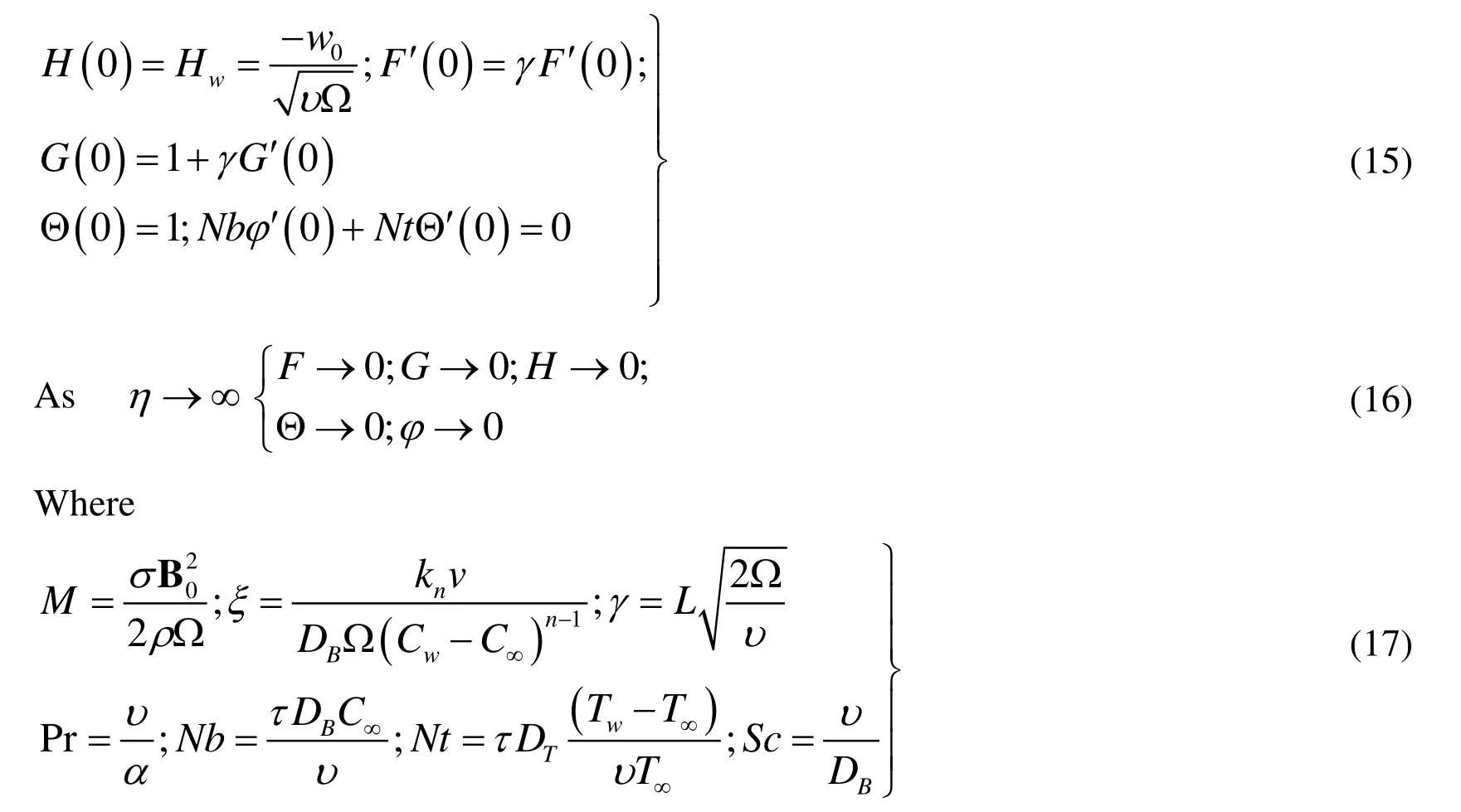
are given in nomenclature and chemical reaction is taken to be of first order.Definitions of the Local Nusselt and Sherwood numbers are given as:

3 Solution procedure

In order to solve the system of Eqs. (10)-(15) with boundary conditions (16)-(17), we use homotopy analysis method for which the following homotopies are constructed

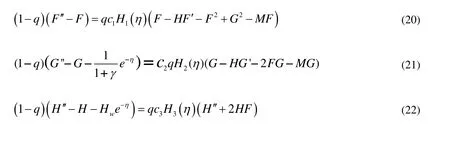
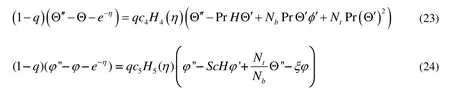
The solutions of the homotopies (21)-(25) can be represented by the series

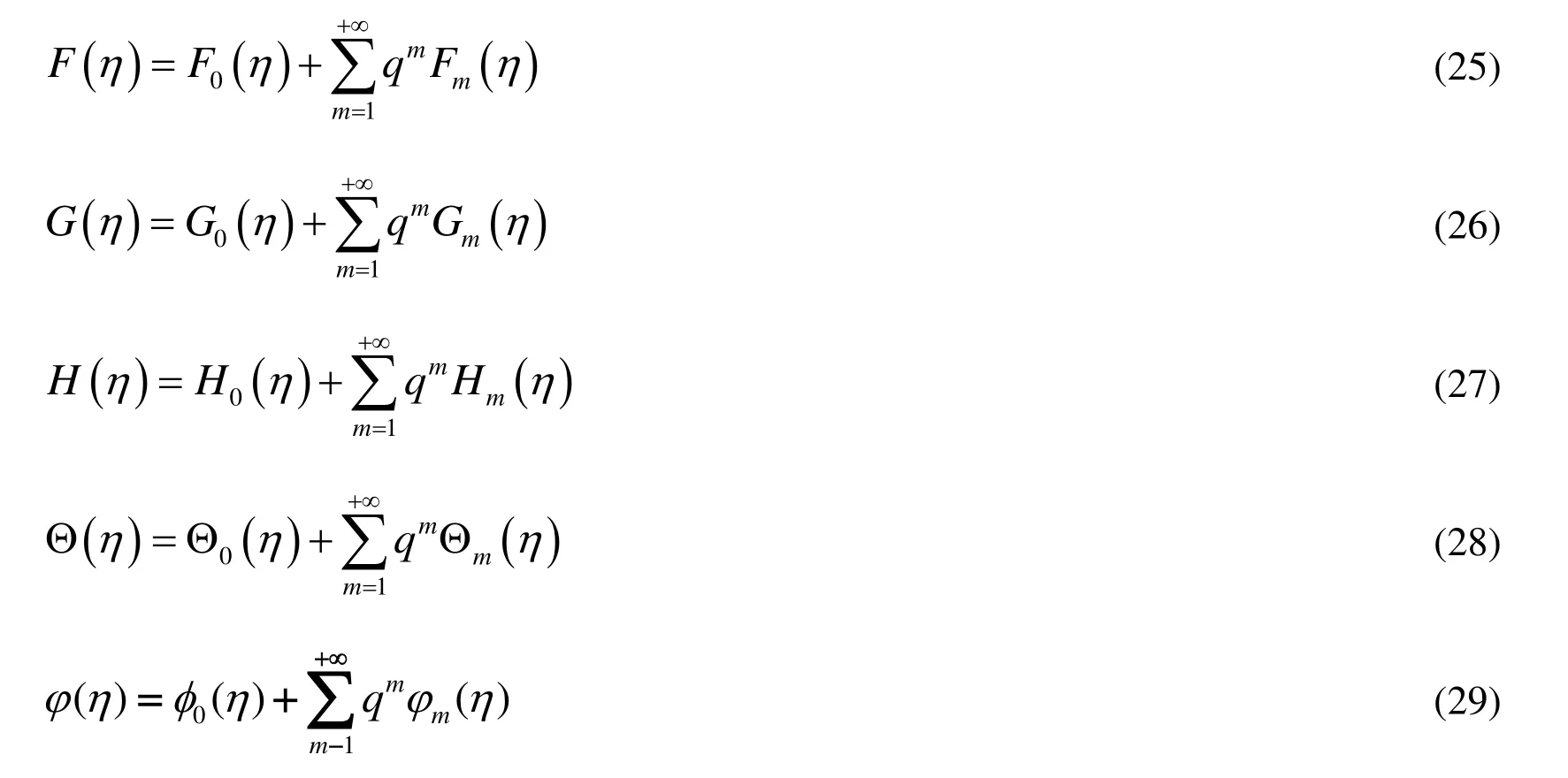
Whereq∈[0,1]is an embedding parameter. Substituting the series (26)-(30) in (26)-(30)and comparing the coefficients of like powers ofqto collect the following linear equations with boundary conditions:

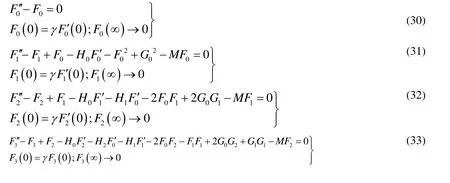
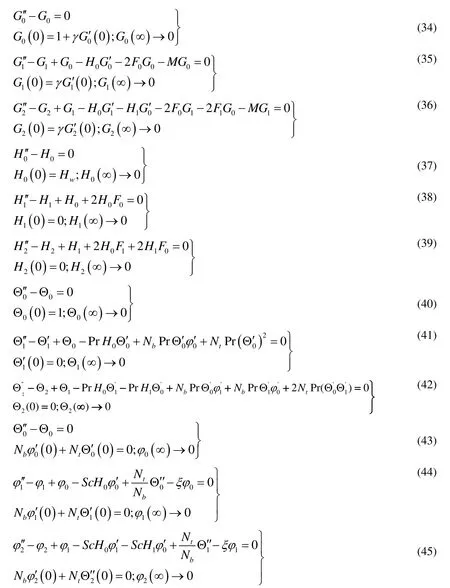
Solving above equations with initial approximations. Thus zero components of approximate solutions are:

Initial approximations satisfy their corresponding boundary conditions. Thus series solution can be obtained by using the following substitutions

Utilizing the Mathematica based HAM package bvph2.0 with the following linear operators, auxiliary parameters and the choice of auxiliary functions respectively.

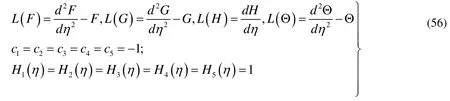
The results obtained are analyzed graphically in the next section.

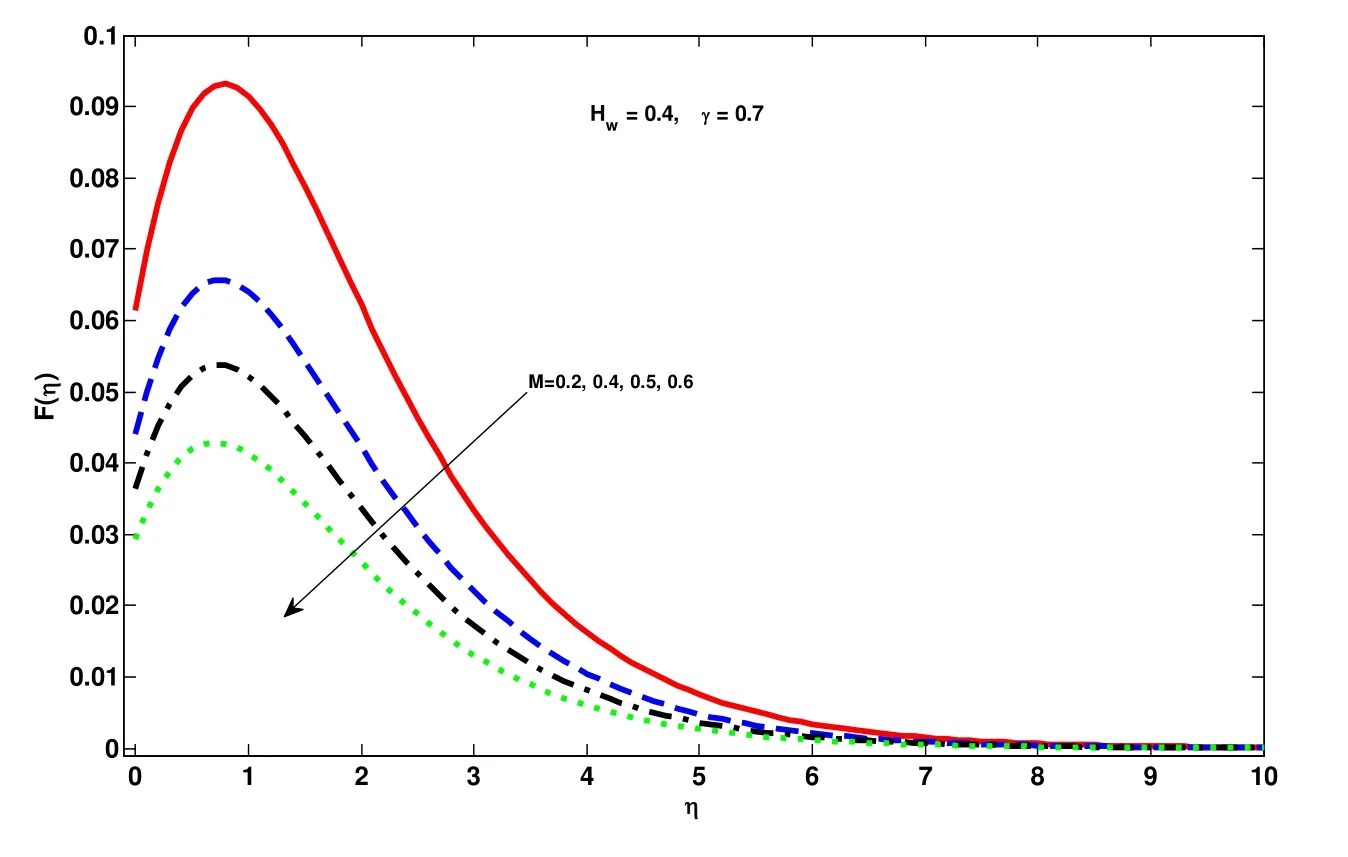
Figure 2: Effect of magnet number M on F(η)

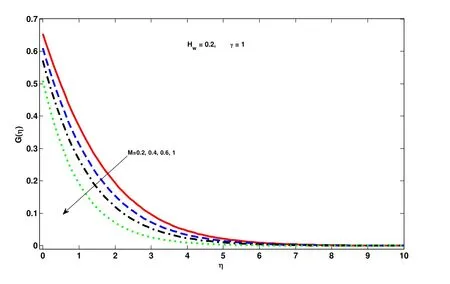
Figure 3: Effect of magnet number M on G(η)

Figure 4: Effect of slip parameter γon F(η)

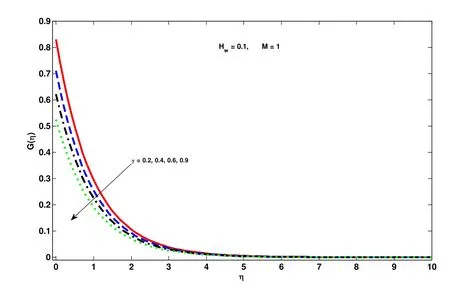
Figure 5: Effect of slip parameter γon G(η)

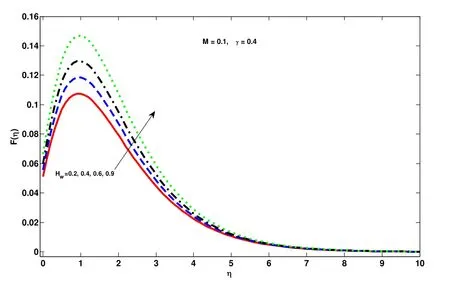
Figure 6: Effect of suction parameter HWon F(η)

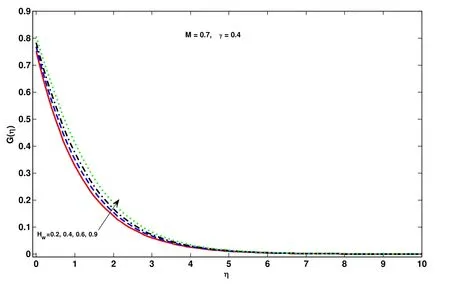
Figure 7: Effect of suction parameter HWon G(η)

Figure 8: Effect of suction parameter HWon H(η)

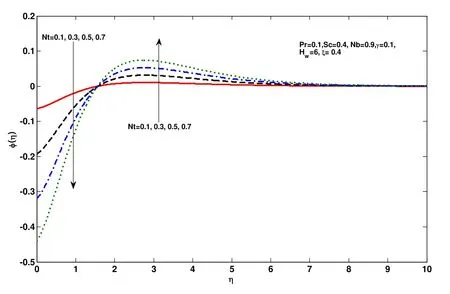
Figure 9: Effect of thermophoresis N( t )on ϕ (η)

Figure 10: Effect of Chemical reaction parameter ξon ϕ (η)

4 Results and discussion

Before going to discuss in detail we first observe that the Tab. 1 confirms the authenticity of present work in modeling and solution technique as well. Fig. 2 to Fig. 10 are about the behavior of velocity profile, temperature profile and concentration profile against various physical parameters. Lorentz Force is entailed by magnet number which causes resistance in fluid movement. Hence corresponding to every bigger quantities of magnetic number, velocity profile and layer thickness of the parabolic and azimuthal velocity components at the boundary decreases shown in Fig. 2 and Fig. 3, respectively.Impact of speed slip number on the fluid velocity components is drawn in Fig. 4 and Fig.5 wherein growing values of slip number decreases the layer of thickness and fluid velocity. Effect of suction parameter on the velocity components is displayed in Figs. 6-8.It is observed that on increasing the suction parameter velocity components are increasing significantly. Nanospecies transit from hot regions to the colder ones is because of thermophoresis. Thus boom in thermophoretic parameter uprights and enhance the concentration profile and its layer shown in Fig. 9. Fig. 10 is drawn to show relation between chemical reaction and concentration profile. Growth within the parametric values of chemical reaction increases the concentration of fluid in rarer and lighter regions. Tabs. 2 and 3 are witnessing the increasing behavior of Sherwood number but decreasing of Nusselt number. Combined effect of different physical parameters on local Nusselt and Sherwood number are displayed in Tab. 4.

5 Conclusions

In this study we observed an MHD nanofluid flowing over the rotating disk with chemical reaction and some of the dominating facts are enlisted underneath:

• Velocity and temperature fields have opposite behavior on booming quantities of magnet number. Former increases while the latter one reduces.

• Growth of speed slip parameter reduces the velocity fields.

• Concentration profile has increasing behavior on growing values of thremophoretic parameter.

• Chemical parametric growth declines and reduces the concentration profile.

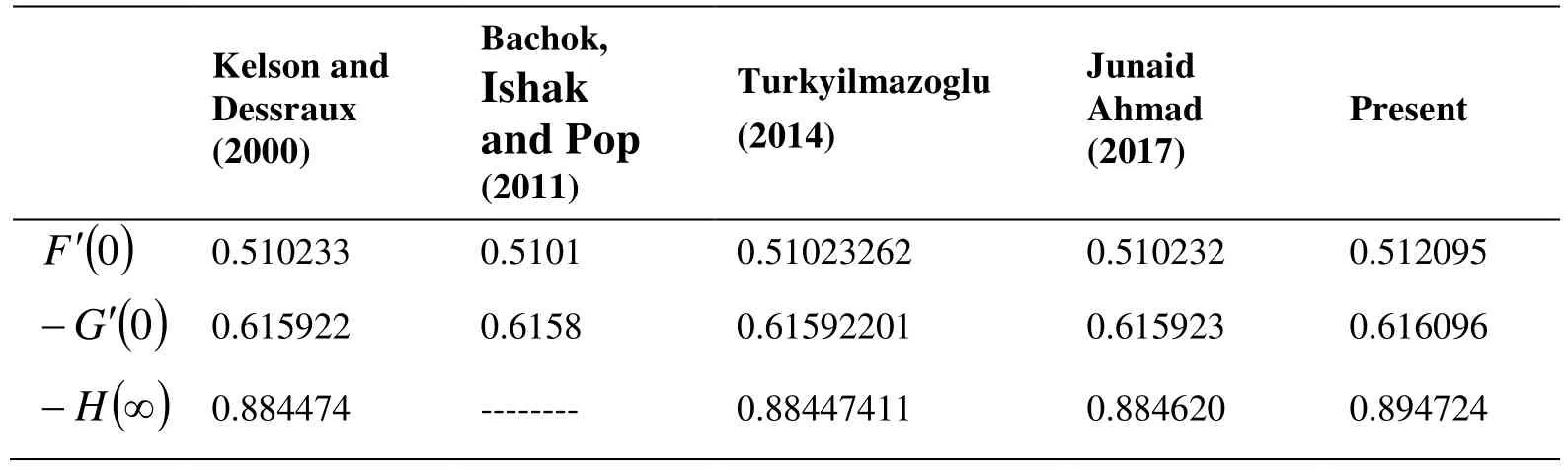
Table 1: Comparison of some results of local Nusselt and Sherood numbers with previous works

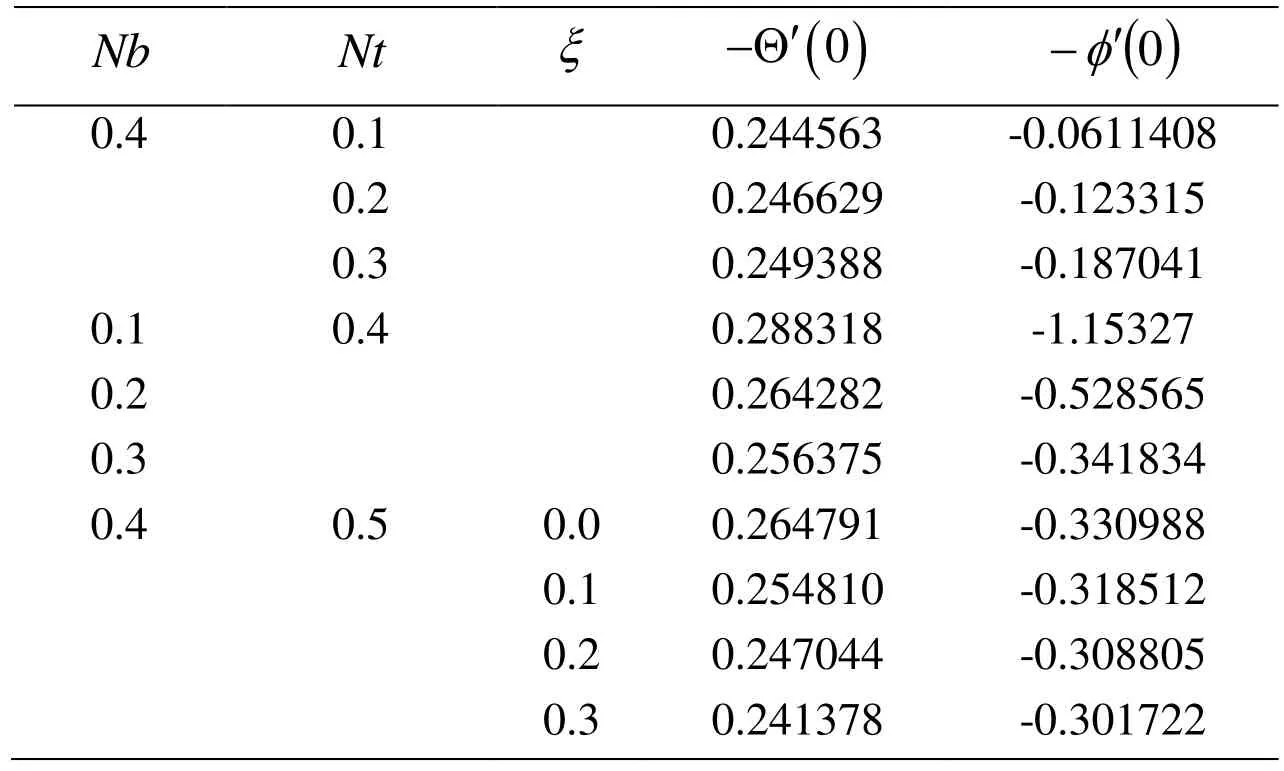
Table 2: Values of Nusselt number and Sherwood number with M =0.1,Hw =0.4,γ=0.4,Pr=1,Sc =0.7,γ1= -0.07079

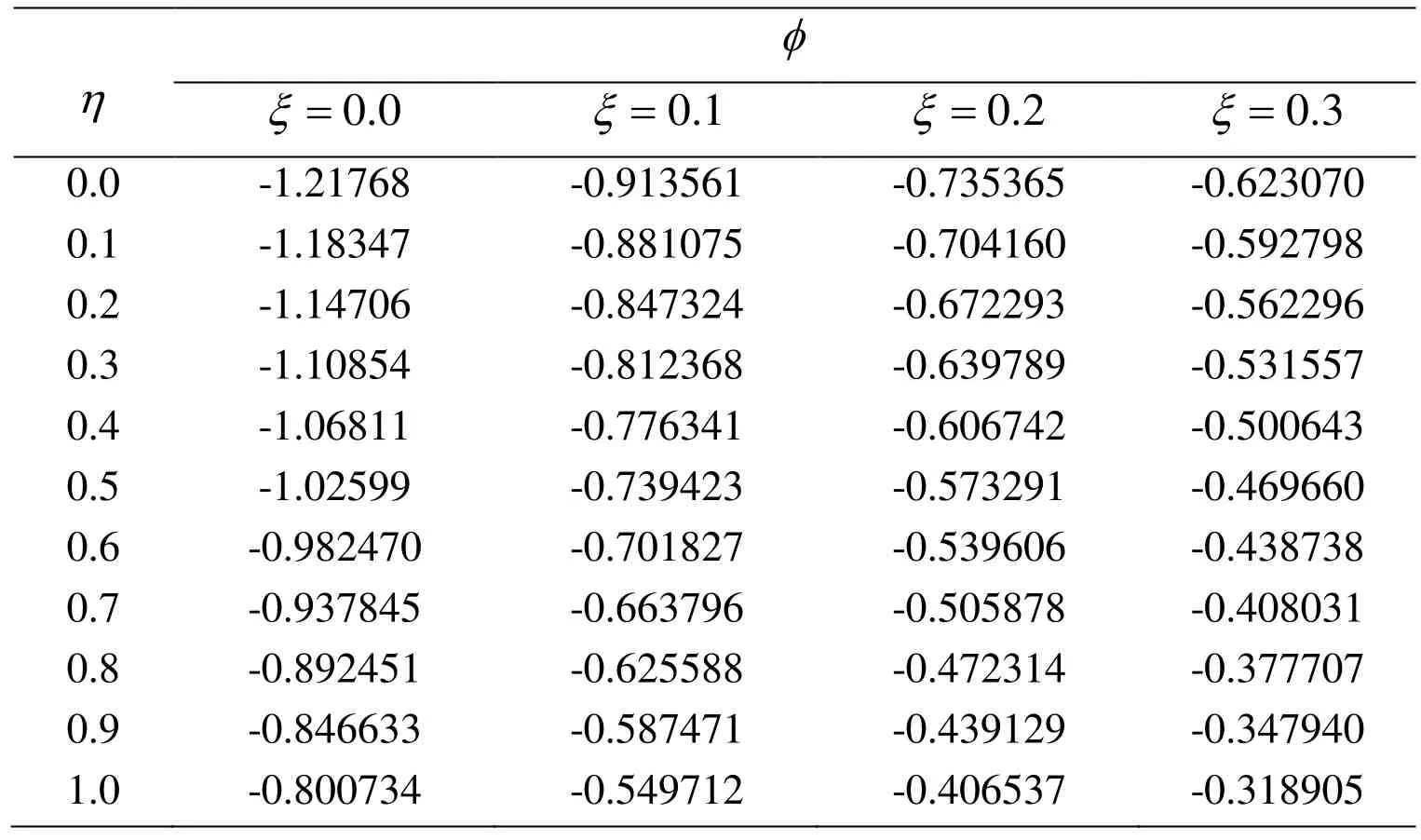
Table 3: Tabulated data corresponding to Fig. 10