Investigation on Purine Corrosion Inhibitions via Quantum Chemical Calculation

Fengjuan Wang , Shengping Wu , and Jinyang Jiang ,

Abstract: Corrosion inhibition performances of three purine derivatives were investigated systematically by employing DFT and molecular modeling. The relationship between macroscopic inhibition efficiency and quantum chemical properties was discussed from multiple perspectives, based on frontier orbital theory, and Fukui function theories. Comparative experimental and theoretical studies were taken, indicating the inhibition efficiency could be analyzed in the order of guanine <2,6-diaminopurine <2,6-dithiopurine. The sulphur atom (S5) was validated to be the most susceptible site for electrophile via quantitative surface analysis.

Keywords: Acid solutions, acid inhibition, DFT calculation, mild steel, modelling studies.

1 Introduction

Steel corrosion in aggressive media is one of the dominant challenges, leading to large maintenance costs in many industries [Cabrera (1996); Lin, Liu and Xiang (2009)].Therefore, corrosion inhibitions for mild steel in acidic medium have been investigated in considerate detail [Ferreira, Giacomelli, Giacomelli et al. (2004); Lagrenee, Mernari,Bouanis et al. (2002); Li, He, Zhang et al. (2008); Okafor, Ikpi, Uwah et al. (2008);Bentiss, Lagrenee, Traisnel et al. (1999)]. Consensus has been reached that significant inhibition efficiency attributes from the presence of electronegative atoms, such as oxygen, nitrogen and sulphur in heterocyclic rings [Khaled (2003); Markhali, Naderi,Mahdavian et al. (2013); Khalil (2003); Mishra, Paik and Atluri (2009)].

Due to the specific structures and properties, purine and its derivatives, including guanine,2,6-diaminopurine and 2,6-dithiopurine, displayed in Fig. 1, have been found promising for corrosion prevention [Yan, Li, Cai et al. (2008)]. However, the inhibition efficiency depends not only on the structure of inhibitor molecule itself, i.e. some quantum parameters like energy gap, polarizability, diploe moment, electron density and the reactive sites for the formation of metallic complex, but also on the characteristic of the environment in which it reacts with and the nature of metal surface. Recent efforts have shown that there exists a correlation between experimental inhibition efficiency and calculated molecular properties [Yadav, Behera, Kumar et al. (2013); Ahamad, Prasad and Quraishi (2010); Kosari, Moayed, Davoodi et al. (2014); Verma, Olasunkanrni,Ebenso et al. (2016); Sasikumar, Adekunle, Olasunkanmi et al. (2015); Solmaz (2014);Bouanis, Tourabi, Nyassi et al. (2016)].

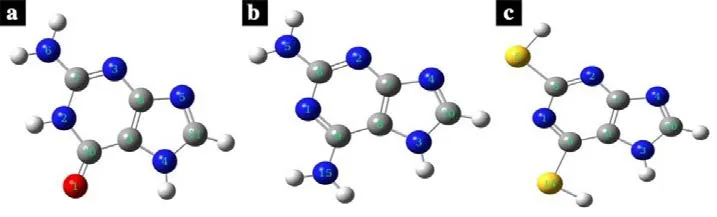
Figure 1: Optimized molecular structures of purines: (a) guanine; (b) 2,6-diaminopurine;(c) 2,6-dithiopurine. The grey ball represents Carbon, blue represents Nitrogen, yellow represents Sulfur, red represents oxygen while the white ball represent hydrogen

In this work, molecular structures, dynamic properties and the reactivity for electrophile reactions have been explored, by using DFT and molecular modeling. The relationship between inhibition efficiency and quantum chemical properties has been interpreted via DFT calculations. More in detail, this paper provides a systematic approach to predict the reactive sites for electrophilic attack, which covers Fukui functions, quantitative surface analysis, and combines with atoms in molecules (AIM) theory.

2 Simulation methodology

In the present study, DFT calculations were performed on Gaussian 03 software package[Frisch (2004)]. Optimized geometries and several quantum chemical parameters of purines were obtained, using the B3LYP/6-311G (d, p) functional and basis set [Becke(1993); Lee, Yang and Parr (1988)], which proved reliable and efficient on relevant systems [Wang, Li, Sun et al. (2012); Guo, Zhu, Zhang et al. (2014)]. In consequence,vibrational frequency analysis was carried out for optimization confirmation. Considering the wide use in non-electrostatic interactions [Rayne and Forest (2010); Zevatskii and Samoilov (2011)], the self-consistent reaction field theory based on Marenich, Cramer and Truhlar’s solvent model SMD is employed [Marenich, Cramer and Truhlar (2009)].Additionally, quantitative analysis of the molecule like Fukui function distribution,electrostatic potential and other integrated properties were implemented with the aid of Multiwfn, version 3.3.8 [Lu and Chen (2012)]. The trajectories were visualized and plotted using VMD software, version 1.9.2 [Humphrey, Dalke and Schulten (1996)].

3 Results and discussion

The research on purines and its derivatives as corrosion inhibitors for mild steel in acid solution, including guanine, 2,6-diaminopurine and 2,6-dithiopurine, was conducted experimentally. Multiplicate experiments were performed to make it reproducible and reliable, which covered weight loss measurements and electrochemical tests in our previous work [Yan, Li, Cai et al. (2008)]. Tab. 1 is quite revealing in several ways. It is apparent that the corrosion rate decreases in the presence of inhibition, in the order of guanine <2,6-diaminopurine <2,6-dithiopurine. Furthermore, the corrosion inhibition efficiency has a significant correlation with the inhibitor concentration, especially for 2,6-dithiopurine, reaching 86.3% at 1.0×10-3M.

Table 1: Efficiency of inhibition (g, %) of corrosion of mild steel in 1 M HCl solution by different concentrations of Guanine, 2,6-Diaminopurine and 2,6-dithiopurine, as determined by comparative experimental techniquesa

Accordingly, to clarify the nature of inhibition efficiency of purines along with the effect of structural parameters, quantum chemical calculations were employed. Some quantum chemical parameters, including the energy of the highest occupied/lowest unoccupied molecular orbital (EHOMO/ELUMO), the energy gap (△E) between HOMO and LUMO,molecular dipole (μ), polarizability (ɑ), global softness (S) and total energy (TE) are all listed in Tab. 2, which are responsible for reactive abilities.

Table 2: Some quantum chemical parameters for purinesa

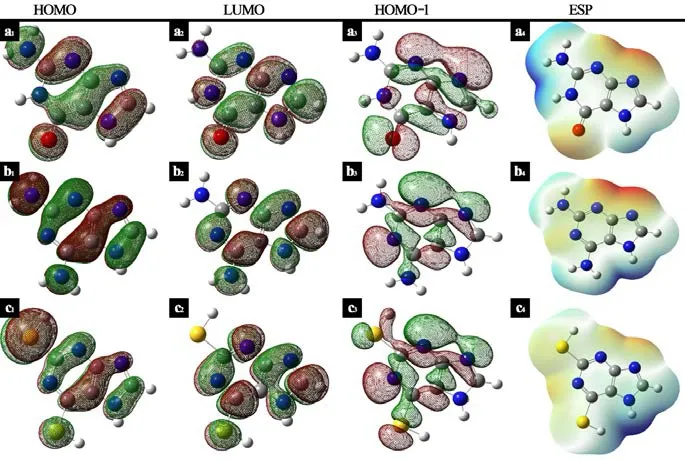
Figure 2: The frontier molecular orbital density distribution and electrostatic potential(ESP) map of purines in gas: (a) guanine; (b) 2,6-diaminopurine; (c) 2,6-dithiopurine

The isosurfaces in red represent the positive values while the green maps are the negative values.

In order to acquire more details, frontier molecular orbital density distribution for purines was shown in Fig. 2. It is evident that the studied orbitals display in a similar shape,which covers the most of the molecular skeleton. In the case of HOMO, it consists of n type long- pair electrons like N, O and S, π-bonding along the N-C linkage and the π-type bonding in the heterocycles. All these aspects should attribute to the resemblance of EHOMO, sharing a similar electron distribution density. Considering LUMO, the difference of ELUMOmay lie in the electron delocalization. Firstly, the orbital density distribution of 2,6-dithiopurine at the position of S14is stronger than other purines, which indicates 2,6-dithiopurine has the ability to accept electron from 4s orbital of Fe preferentially.Furthermore, π-electrons delocalization in the heterocycles plays a quite significant role,as indicated in Fig. 2(c2). Electrons in the occupied molecular orbitals HOMO-1 have relatively energetic electrons to interact with Fe atoms. In comparison of these three inhibitors, there exists a tendency that the degree of electron-delocalization increase slightly,in the order of guanine <2,6-diaminopurine <2,6-dithiopurine, which is consistent with the inhibition efficiency.

Although some calculations between HOMO/ LUMO and inhibition efficiency have been performed earlier, no direct and positive relationship has been found yet [Bentiss,Traisnel, Vezinet al. (2003)]. Generally, another quantum chemical parameter considered in corrosion science is the energy gap (△E), which is regarded as a remarkable parameter to measure the reactivity of the inhibitors [Ahamad, Prasad and Quraishi (2010)]. It is commonly believed that inhibition efficiency increases as △E decreases. Naturally, a higher energy gap clarifies the inhibitor molecule is more stable and also revealed by total energy (TE) in Tab. 2. What’s more, △E is related to softness and polarizability,which can be characterized by molecular dipole (μ), polarizability (ɑ) and global softness(S) in Tab. 2.

The polarizability ɑ is a symmetric matrix, implying the difference of polarizability in different directions. In order to facilitate comparison of overall polarizability between various systems, the isotropic average polarizability ɑ is defined as ɑ=(ɑxx+ɑyy+ɑzz)/3. It is recognized that higher value of ɑ may result in better inhibition efficiency and stronger adsorption process [Kandemirli and Sagdinc (2007)].

The theoretical basis for absolute hardness (η), global softness (S) lies in the density functional formalism and the operational definitions are as follows [Yang and Parr(1985)],

where I and A are the ionization potential and electron affinity of any chemical system,atom, ion, molecule, or radical.

Previous studies suggest that soft molecules, with a small energy gap, will be more polarizable than hard one. Additionally, molecule with a higher globe softness (S), will undergo reactions more readily, such as dissociation and isomerization [Yang and Parr(1985)]. All these conclusions could be supported by the data listed in Tab. 2, which shares the rule, inhibition efficiency increases with higher value of polarizability (ɑ) and global softness (S).

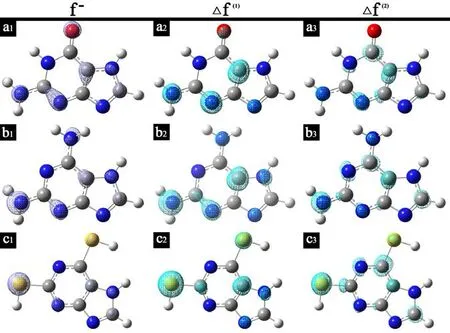
Figure 3: Fukui function and dual descriptor distribution: (a) guanine; (b) 2,6-diaminopurine;(c) 2,6-dithiopurine. The isodensity contours are 0.005 electron bohr-3

Compared to the experimental data, the trend of inhibition efficiency obtained theoretically is in highly agreement, which means quantum chemical calculation could solve this problem in essence. Unfortunately, these parameters above could only characterize the overall properties of the inhibitor molecule, the analysis of reactive sites is hardly resolved.

The initial uses of electrostatic potential in studies of chemical reactivity are in predicting sites and relative reactivities toward electrophilic attack [Murray and Politzer (2002);Politzer and Murray (2007)]. Electrostatic potential on the 0.001 a.u. molecular surface of three purines are illustrated in Fig. 2. In general, negative electrostatic potentials are often found to be associated with affinities of the various sites toward electrophilic attack, as shown in the red region like O1, S5in Fig. 2. Although, such reasoning has had some success in literature [Yan, Li, Caiet al. (2008); Wang, Li, Sunet al. (2012)], but is not reliable, which shall be discussed in more detail later in this article.

Another approach available to demonstrate the reactive sites is Fukui function, which is an important concept in conceptual density functional theory, and has been widely used in predicting reactive sites [Yang and Parr (1985)]. It is defined as

whereNis the number of electros in present system, the constant termvin the partial derivave is external potential. In the finite difference approximation, Fukui function can be calculated unambiguously for the two situations below:

Apart from this, dual descriptor is another beneficial function to manifest reactive sites[Morell, Grand and Toro-Labbe (2005)], which is in dispensable with Fukui function.

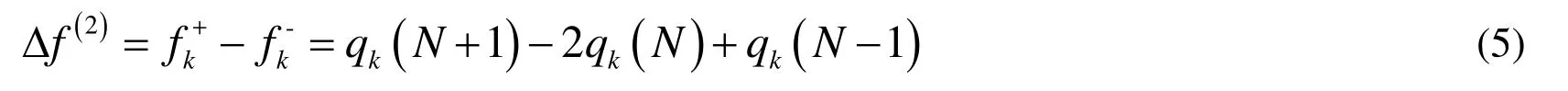
Worthnotingly, dual descriptor can also be evaluated in terms of spin density ρs.

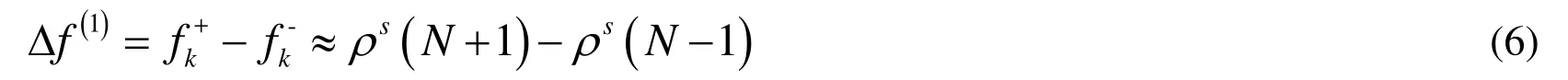
From Fig. 3 above, it may be inferred the most favorable reactive sites for electrophilic attack in three purines are located in O1, N5and S5respectively, with the most positive part off−function delocalization. When it comes to ∆f(the negative isosurfaces are visualized which represent the capacity for electrophilic attack), the result of preferential sites for electrophilic attack is in accordance with Fukui function, implicitly validating the reactive sites prediction. Nevertheless, there still exist some unanswered problems that the exact form ∆f(2), does not necessarily give rise to better result than ∆f(1), using spin density approximate evaluation, which was also proposed by Morell [Morell, Grand and Toro-Labbe (2005)].

Fukui function and dual descriptor examined in visualization manner have obtained the conclusion. Nonetheless, visual analysis is somewhat ambiguous and the discussion is inconvenient to be compared in literature. Therefore, condensed Fukui function and condensed dual descriptor are utilized, combined ionization potential and electron affinity addressed before for quantitative comparison between difference inhibitor molecules.

According to Tab. 3, it is obvious that 2,6-dithiopurine has the highestf−associated with S5and S14, which means these sites are the most reactive for electrophilic attack with the metal. This is also supported by electrostatic potential maps in Fig. 2 and Fukui function distribution in Fig. 3. However, considering each inhibitor molecule alone, it is found that O1, N5, S5are most prone for donating electrons respectively, while the positively charged regions are located at O1, C10, S14atoms, individually, for nucleophilic attack. In consequence, emphasis should be placed that good inhibition efficiency should be attributed to the large number of reactive sites on the inhibitor molecules, for both nucleophilic and electrophilic attack.

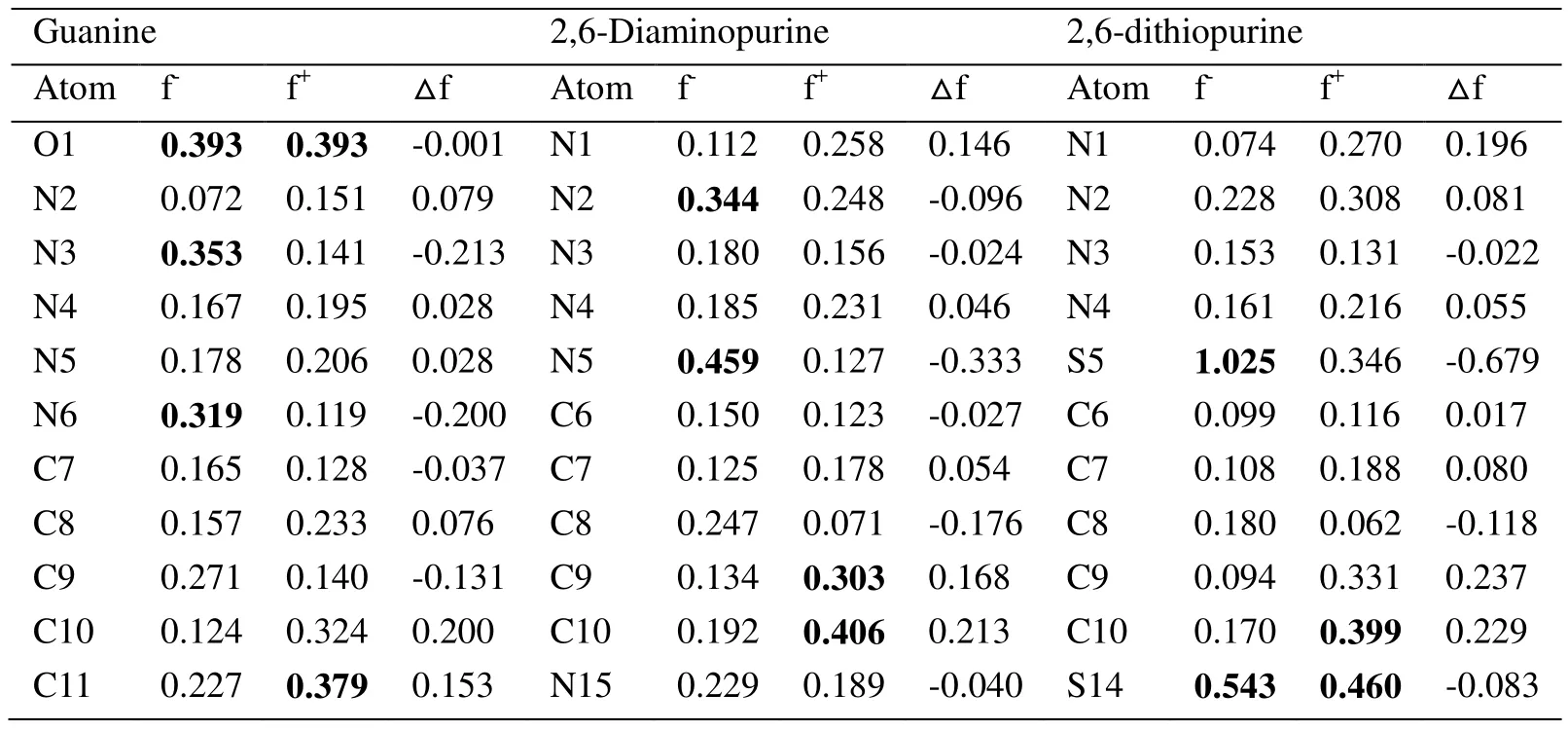
Table 3: Modified condensed (atomic) Fukui functions for purines calculated by using the Hirshfeld population analysis method

In brief, comparing the properties calculated above, the evidence begins to accumulate that there exists a potential relationship, between inhibition efficiency and quantum chemical parameters. Anyway, it offers an operative solution to give some explanations of the inhibition performance for mild steel in acid solution.

4 Conclusions

In the present study, the nature of purine corrosion inhibitions has been discussed by using DFT calculations at the B3LYP/6-311G (d, p) level combined with population analysis, topological analysis as well as quantitative analysis of molecular surface.

The correlation between inhibition efficiency and quantum chemical properties has been established and verified by experimental observation. Comparative experimental and theoretical studies indicate the inhibition efficiency in the order of guanine <2,6-diaminopurine <2,6-dithiopurine.

Acknowledgement:The authors greatly acknowledged the support from National Natural Science Foundation of China (No. 51438003, No. 51508091, No. 51578143).This work was also supported by the National Basic Research Program of China “973 Project” (No. 2015CB655105). We were grateful to the High Performance Center (HPCC)of Nanjing University for doing the numerical calculations in this paper on its IBM Blade cluster system.