混合时间窗约束下多式联运最优路径选择研究

吕学伟，杨 斌，黄振东

（上海海事大学 物流科学与工程研究院，上海 201306）

0 引言

在现实的运输过程中，公路运输自由灵活，而铁路、水路和航空运输都有固定的到达时间和离开时间，货物需要在运输工具离开之前到达相应的节点位置，并完成相应的装载任务，否则只能等待下一班次。对于收货人而言，也存在一个收货时间段，而这个时间段一般比较宽松。因此，在实际的运输过程中，存在着运输方式硬时间窗和收货人收货的软时间窗组合而成的混合时间窗。

对于收货人的软时间窗，国内外的研究均较多，而对于运输方式硬时间窗的研究，则国外的研究相对较多。Ziliaskopoulos 等[1]以铁路、航空、水运等运输方式的固定出发时刻表为约束条件，建立单目标或多目标模型，寻找最优运输路径和运输方式的组合；Chang[2]研究各节点处各种运输方式的硬时间窗，并采用标号法寻找多目标下的最优路径和运输方式组合；Cetin 等[3]重点研究收货人的硬时间窗要求，规定在特定时间段内将货物送达到收货人的手里，以此为约束条件进行多式联运最优路径的优化；Marjani 等[4]以运输过程中的软、硬时间窗为约束条件，进行整车多式联运、空箱调运等路径优化；付晓凤等[5]综合考虑危险品多式联运过程中的安全性和经济性，建立基于危险性最小，以及成本、时间最少的联运方案优化模型；黑秀玲[6]对时间窗进行敏感性分析；赖志柱[7]考虑到各节点处的软时间窗，创立和声搜索算法优化运输路径；邹宗峰等[8]以各个运输节点上的软、硬时间窗为约束，组成混合时间窗，采用加权法处理多目标优化问题；梁晓慷[9]在考虑模糊运输时限时间窗的基础上，以运输费用最小、客户满意度最高为优化目标，构建多式联运路径优化问题的线性规划模型；杨江波[10]从实际运输情况出发，考虑到公路运输自由灵活，而铁路、航空、水运在各个运输节点处都有固定的发车时刻表，以这些固定时刻表为约束条件，建立总运输成本最低的优化模型，采用蚁群算法，为多式联运经营人选择最优运输方案。在此，从现实角度出发，研究混合时间窗对多式联运最优运输方案的影响，以总成本最低为目标，构建混合时间窗约束下多式联运最优路径选择模型，并通过案例进行验证。

1 混合时间窗约束下多式联运最优路径选择模型构建

1.1 问题描述及假设

将一批货物从起始城市O运到终点城市D，采用集装箱运输方式，中间有多个节点城市，构成集合N，每个节点城市又有多种运输方式，所有运输方式构成集合K，在每个节点城市都可以转换运输方式。每个节点城市发往下一个节点城市的铁路、水路运输都有固定的到达和离开时间，而收货人在收货时有比较宽松的时间段。以铁路运输、水路运输的硬时间窗和收货人的软时间窗组成的混合时间窗为约束，并以总的运输成本最小为目标，为承运人选择最优的运输方案。

假设在运输途中货物没有被分割运输，货物状态不发生任何变化，运输工具和中转工具的载运能力充足，能满足集装箱的运输需求。

1.2 模型构建

以总运输成本最低为目标，以混合时间窗为约束条件，构建多式联运最优路径选择模型如下。

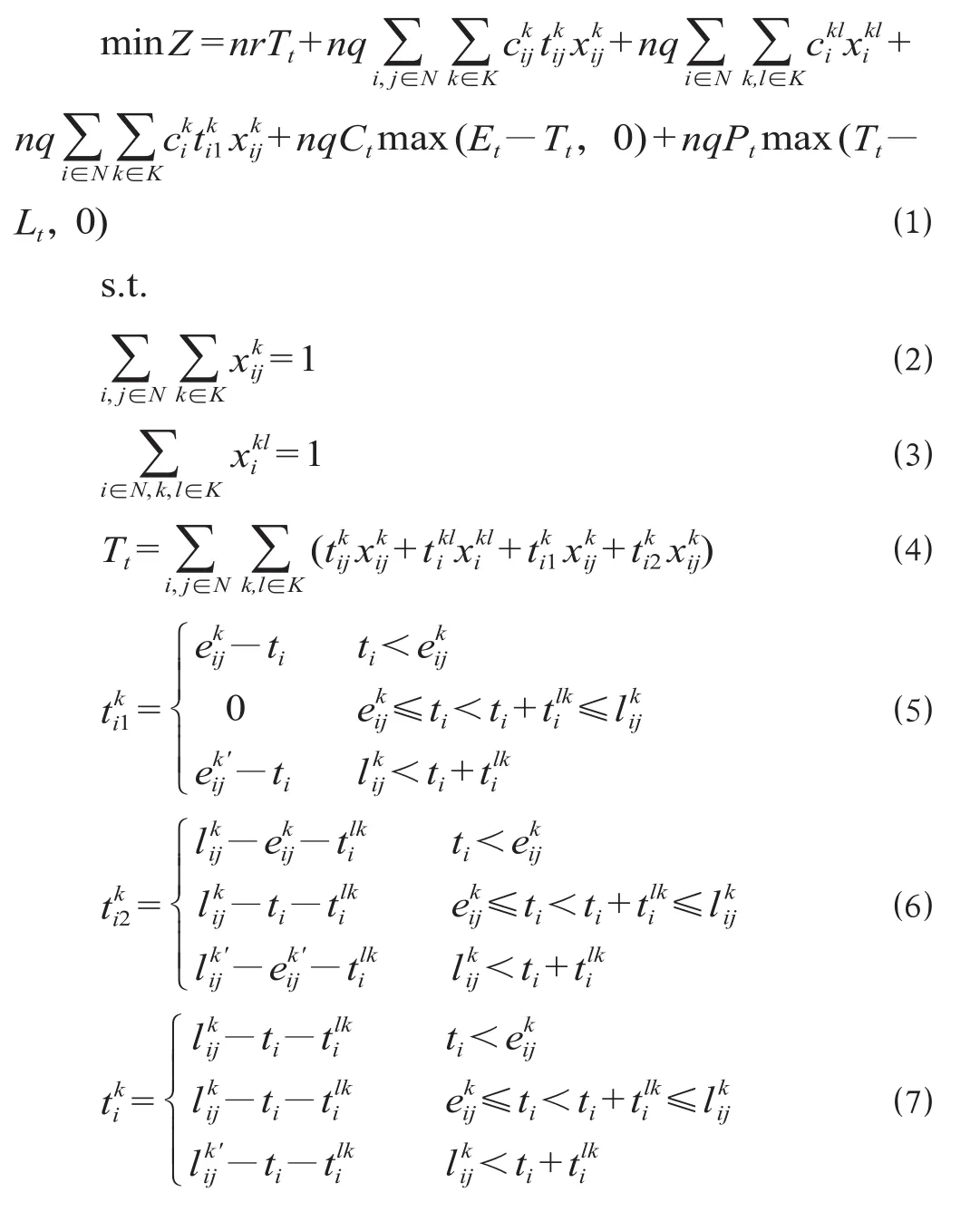
式中：Z为总的运输成本；n为集装箱的标箱数；r为 1 标箱集装箱的日租赁成本；Tt为货主收货时间；q为集装箱的重量；为从第i个节点到第j个节点，采取第k种运输方式的单位运输成本；为从第i个节点到第j个节点，采取第k种运输方式的运输时间；为决策变量，当第i个节点到第j个节点采用第k种运输方式时，值为 1，否则为 0；为在第i个节点，第k种运输方式转变为第l种运输方式时的单位中转费用，当k=l时，值为 0；为决策变量，如果在第i个节点处发生转运，则该值为 1，否则为 0；为在第i个节点处采用第k种运输方式的单位等待成本；为在第i个节点处等待第k种运输方式到达的时间，在这个时间段内会发生等待成本；Ct为货物提前到达终点的单位仓储成本；Et为收货人最早收货时间点；Pt为延迟到达终点的单位惩罚成本；Lt为最迟收货时间点；为在第i个节点，第k种运输方式转变为第l种运输方式时的中转时间，当k=l时，值为 0；为在第i个节点处第k种运输方式等待离开第i个节点的时间；为第i个节点发往第j个节点的路线上，第k种运输方式到达第i个节点的时间；为第k种运输方式离开第i个节点的时间；，分别为下一班次，第k种运输方式到达、离开第i个节点的时间；ti为货物到达第i个节点处的实际时间；为第k种运输方式在第i个节点处的总等待时间。

公式 ⑴ 表示总成本最小的函数，总成本包括租赁成本、运输成本、中转成本、等待成本、因偏离收货人收货时间窗而产生的惩罚成本；公式 ⑵表示第i个节点与第j个节点之间只能选择一种交通工具；公式 ⑶ 表示在第i个节点处只能发生一次转运；公式 ⑷ 表示总的运输时间，包括运输时间、中转时间、在节点处等待运输工具到达的时间，以及在运输工具上等待离开节点的时间；公式 ⑸ 表示在各节点处等待运输工具到达的时间，在这个时间段内会发生等待成本；公式 ⑹ 表示在第i个节点处在第k种运输方式上等待离开第i个节点的时间，在这个时间段内不发生等待成本；公式 ⑺ 表示第k种运输方式在第i个节点处的总等待时间，在第i个节点处等待第k种运输方式到达的时间与在第i个节点处在第k种运输方式上等待离开的时间之和，即公式 ⑸ 与公式 ⑹ 之和。

1.3 算法设计

多式联运最优路径选择问题被证明是 NP-hard问题。蚁群算法作为一种模拟进化算法，具有分布式、启发式计算的特点，适合求解多式联运的最优路径选择问题。

在多式联运的起点和终点之间，有n个节点，蚂蚁在转移的节点间释放信息素，并通过信息素的交流来完成最优路径的选择。蚂蚁选择可行的节点完成整个路径，之后由其他的蚂蚁按照剩下的可行节点完成整个路径。当每只蚂蚁到达终点后，进行局部信息素的更新，当所有蚂蚁都到达终点后，进行全局信息素的更新，在经过最大迭代次数后得到最优解，具体求解步骤如下。

（1）初始参数设置。设置蚁群数为m，起始时间为 0，最大迭代次数为NCmax，节点集合为P，读入所有节点处所有运输方式的运输时间、运输成本、中转成本、等待成本、时间窗等信息，设定启发信息和初始信息素，设定蚂蚁结构包括运输信息、线路选择信息、中转信息和到达节点的时间。

（2）对循环次数NC进行迭代，当达到最大迭代次数NCmax时，循环结束。即NC=NC+ 1。

（3）将各节点拆分成进入节点和离开节点，将蚂蚁分配在各节点上，设置禁忌表tabum，记录所有的起始节点。

（4）所有的蚂蚁搜寻满足条件的节点，将第r只蚂蚁每次允许选择的节点加入到候选集合allowedr。

（5）让蚂蚁选择节点的公式可以表示为

式中：(t) 为t时刻，蚂蚁r由第i个节点到第j个节点的概率；(t) 为t时刻路径 (i，j) 上的信息素浓度；ηij为启发函数，表示蚂蚁从第i个节点到第j个节点的期望值，通常取 2 个节点城市间距离的倒数；α为启发式因子，指蚂蚁在移动时积累的信息量的多少对蚂蚁的指导作用相对重要程度；β为期望的启发式因子，指启发信息对蚂蚁搜索的相对重要程度。

对信息素进行更新的公式可以表示为

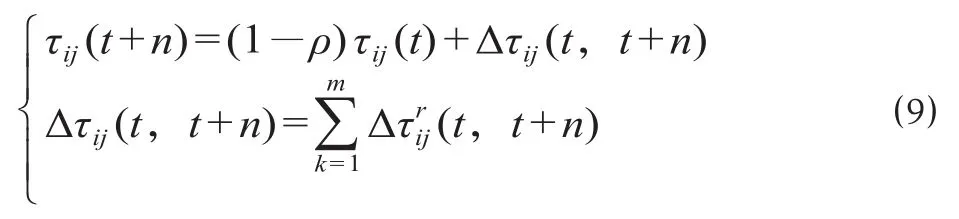
式中：τij(t+n) 为在 (t，t+n) 时间内，循环一次后，蚂蚁在所有路径上更新信息素的规则；ρ为信息素的挥发程度系数；1－ρ为信息素的残留程度系数；Δτij(t，t+n) 为整个蚁群在经过 (t，t+n) 的时间，完成一次循环遍历后，边 (i，j) 上剩余的信息素；Δ(t，t+n) 为蚂蚁r在经过 (t，t+n) 的时间，完成一次循环遍历后，边 (i，j) 上剩余的信息素。

（6）当所有的蚂蚁都完成一次循环后，以总成本最低选择最优蚂蚁。

（7）以最优蚂蚁的信息为依据，对全局进行信息素更新。

（8）当达到最大迭代次数时，循环结束，以步骤（6）的蚂蚁所表示的信息为最优解，否则返回步骤（2）。

2 案例分析

2.1 基础数据

假设现有 10 t 货物采用 20 ft 集装箱从城市O运到城市D，中间有 5 个节点城市，分别记为A，B，C，E，F。每 2 个节点城市之间最多有 3 种运输方式可供选择，分别是公路、铁路、水路。公路运输没有时间窗约束，铁路、水路运输都有固定的时间窗，收货人有收货的软时间窗。各节点间连接方式如图 1 所示。

图 1 各节点间连接方式Fig.1 Connection modes among different nodes

假设公路运输单价是 0.2 元/(t · km)，铁路运输单价是 0.15 元/(t · km)，水路运输单价是 0.02 元/(t · km)，3 种运输方式的速度分别是 60 km/h、60 km/h、30 km/h。假设 3 种运输工具都是匀速运输，而模型是研究时间窗对运输方案的影响，将基于单位运输距离的单位运输成本转化为基于单位运输时间的成本，转化后的运输单价分别为 12 元/(t · h)、9 元/(t · h)、0.3 元/(t · h)。每标箱的日租赁成本是100 元，在铁路车站因提前到达而产生的单位等待成本是 30 元/(t · h)，在码头是 20 元/(t · h)。假设各节点开往下一节点的铁路每天有 4 列，时间窗宽度是 3 h，即在各个节点处，铁路的停留时间是 3 h；船舶每天是 3 班，时间窗宽度是 5 h，即在各个节点处，船舶的停留时间是 5 h。铁路和船舶的进站时间在指定范围内随机生成，货主收货的时间窗是[25，30]，提前到达的单位储存成本是 40 元/(t · h)，延迟到达的单位惩罚成本是 60 元/(t · h)。假设OA1，O－A3弧中的铁路和水运假设都是从 0 ∶ 00 开始出站，即货物从0 ∶ 00 点开始发出。记某节点处某运输方式的服务时间窗表示为 [a，b]，a表示运输工具到达节点的时间，b表示运输工具离开节点的时间。各节点的运输时间参数如表 1 所示，各运输方式间单位转运成本、转运时间参数如表 2 所示，各节点处铁路、水路运输的时间窗参数如表 3 所示。

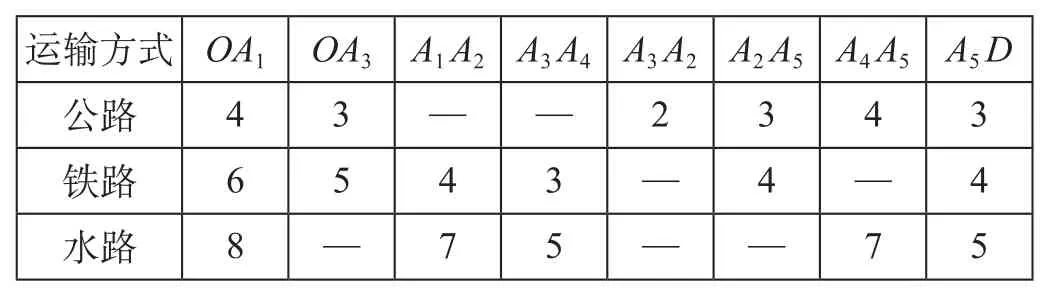
表 1 各节点的运输时间参数 hTab.1 Transport time parameters of each node

2.2 用蚁群算法进行求解

设置相关参数值：初始信息素为 0.1，启发因子α为 2，期望启发因子β为 5，信息素挥发系数ρ为0.05，蚁群规模m为 30，最大迭代次数NCmax为 200。得到的最优解为：OA3A4A5D，运输方式分别为铁路-水运-水运-水运。混合时间窗下最优路径的运行数据如表 4 所示，各运输方式的运行数据如表 5 所示。

2.3 比较分析

节点处没有时间窗约束，相当于货物在中转途中各运输方式无缝对接，这是目前大多数学者的思考模式。当无时间窗约束时，由蚁群算法得到的最优解也为：OA3A4A5D，运输方式为铁路-水路-水路-水路，运行总成本是 717 元，运行时间是 23 h，运输费用为 501 元，转运费用为 120 元，租赁费用为 96 元。

表 2 各运输方式间单位转运成本、转运时间参数Tab.2 Unit transportatn cost and transport time between different transportation modes

表 3 各节点处铁路、水路运输的时间窗参数Tab.3 Time windows for railway and waterway transport at each node

表 4 混合时间窗约束下最优路径的运行数据Tab.4 Operation data of optimal path constrained by mixed time windows

表 5 各运输方式的运行数据Tab.5 Operating data for each mode of transport

将有混合时间窗限制与无混合时间窗限制下最优路径的费用与时间进行对比，成本对比如表 6 所示，时间对比如表 7 所示。

通过对比，无论是总费用、总时间，还是单个费用、单个时间，有混合时间窗约束的数值都要比无时间窗约束的数值高，至少是相等。可见，在现实的运输过程中，因混合时间窗而产生的运输费用不仅真实存在，而且这种数值有时还很大，对多式联运最优运输方案的选择会产生较大的影响。对于多式联运的承运人而言，这种费用和时间不能无视，也就是不能无视混合时间窗的真实存在性，不仅要考虑收货人软时间窗的影响，更要考虑铁路、水路、飞机等运输工具硬时间窗的影响[11-13]。

表 6 成本对比 元Tab.6 Cost contrast

表 7 时间对比 hTab.7 Time contrast

3 结束语

基于运输方式硬时间窗和收货人收货的软时间窗，构成混合时间窗。在此基础上，以总成本最少为目标，将混合时间窗纳入约束条件，建立多式联运最优路径选择优化模型，采用蚁群算法，能更精确和实际地反映多式联运路径选择问题。通过有混合时间窗约束下的最优路径与无混合时间窗约束下的最优路径进行数据对比，无论运输成本，还是运输时间，两者都有很大差距，这表明混合时间窗约束对多式联运最优运输路径的选择具有重要影响，是经营人和承运人不能忽视的重要因素。由于设计的硬时间窗具有固定性，可以考虑随机的硬时间窗进行深入研究，包括时间窗的宽度和时间窗的位置，以反映更为真实的运输特征。