一种最大置信上界经验采样的深度Q网络方法

朱 斐 吴 文 刘 全,3 伏玉琛,4

1(苏州大学计算机科学与技术学院 江苏苏州 215006)2(江苏省计算机信息处理技术重点实验室(苏州大学) 江苏苏州 215006)3(符号计算与知识工程教育部重点实验室(吉林大学) 长春 130012)4 (常熟理工学院计算机科学与工程学院 江苏常熟 215500) (zhufei@suda.edu.cn)

强化学习(reinforcement learning, RL)能完成从环境状态到动作映射的自我学习过程[1]，智能体(agent)与环境交互，选择并执行动作，环境对此作出反应，进入下一个状态，利用价值函数评估状态，不断调整策略，反复迭代，直到结束.强化学习通过寻求agent在环境中获得的最大累积奖赏值，获得最优策略.强化学习是目前机器学习领域的研究热点之一，已经在优化调度、游戏博弈等领域中得到了良好的应用[2-4].深度学习(deep learning, DL)是机器学习的另一个研究热点，其基本思想是自主地从原始输入数据中组合底层特征，形成更抽象的高层来表示属性类别或特征.深度学习的一些方法已经成功地应用于图像处理、自然语言处理等多个领域[5-7].

目前，越来越多的任务以复杂数据为输入，以求解最优策略为目标.这就需要将深度学习和其他机器学习方法结合起来.谷歌人工智能团队DeepMind将深度学习和强化学习结合在一起，形成了深度强化学习(deep reinforcement learning, DRL)，开启了从感知到决策的端对端(end to end)的研究.深度Q网络(deep Q-network, DQN)[8-9]是深度强化学习的一个著名方法，其结合了深度卷积神经网络(convolutional neural network, CNN)和强化学习中的Q学习(Q-learning)算法[10]，成功地用于解决高维输入环境中学习策略的任务.深度Q网络方法可以将未经处理的图片直接作为输入，在处理视觉控制问题中具有通用性；在一些Atari 2600游戏中，深度Q网络达到了能与人类玩家媲美的水平.

可是，传统的强化学习算法存在着一些问题，使之不能很好地与深度学习方法结合.例如，在传统的强化学习算法中，每观察到一次状态转移就要更新一次参数.这会带来2个问题：1)参数更新在时间上是相关的；2)出现次数少的转移样本容易被忽视.而大多数深度学习算法需要满足2个重要条件：1)训练样本之间的关联程度低；2)训练样本在训练期间可以被重复使用多次.经验回放(experience replay)方法可以较好地解决这些问题[11-12].经验回放方法将历史样本放到经验池中，每次选择小批量(mini-batch)样本计算损失函数并更新网络参数.深度Q网络也使用了经验回放方法，agent可以在线地存储和使用其与环境交互得到的历史样本.在每个时刻，agent等概率地抽取小批量的转移样本进行训练，以保证小概率出现的样本也能够有机会保存在经验池中.经验回放方法打破了学习样本中存在的关联性，不仅使训练过程更易于收敛，而且提高了数据的利用率.但是，经验回放方法仅简单地使用等概率的方式对经验池中的数据进行采样.事实上，在经验池中的转移样本对参数训练的作用是有所不同的：有些转移样本会产生较大的作用，有些则反之.而经验回放方法的采样方式很难区分不同样本的重要性.Schaul等人[13]提出一种基于时间差分误差(temporal difference error, TD-error)的优先经验回放(prioritized experience replay, PER)的采样方式，以TD-error评估样本，认为TD-error大的样本重要性程度高，应赋予较高的被选概率.该方法能更好地利用经验池中的重要样本，但是由于经验池容量通常是固定的，且训练时采用的批量样本数量较少，因此会存在一些样本未被使用就被舍弃的情况.这一不足使得样本多样性的要求无法得到满足，结果使得学习效率低下.

针对此问题，本文提出了一种新型的采样机制，有效地避免了上述问题.一方面，在采样过程中利用最大置信上界(upper confidence bound, UCB)的基本思想[14]，提出了基于最大置信上界采样算法(upper confidence bound sample, UCBS)，给经验池中未被使用过的样本附加一个鼓励项，提高其被选取的概率，从而保证样本的多样性；另一方面，增加能使agent学习到更多信息的样本的被选概率.由于本文方法使用奖赏值来衡量agent从样本中学习信息的优劣，因此，本文方法会倾向于选择可能获得更高奖赏样本，进而使agent能够更快地学习到最优策略.

1 相关工作

1.1 强化学习

在强化学习中，从时间步t开始到时间步T情节结束时所获得的累积折扣奖赏定义为

(1)

其中，0≤γ≤1是折扣因子，表示未来奖赏对累积奖赏的影响力度.

在强化学习模型下，agent在时间步t的状态xt下，执行根据策略h选择动作u，环境对智能体所执行的动作给出反馈，给agent下一时间步的状态xt+1和奖赏rt+1.强化学习模型框架示意图如图1所示:

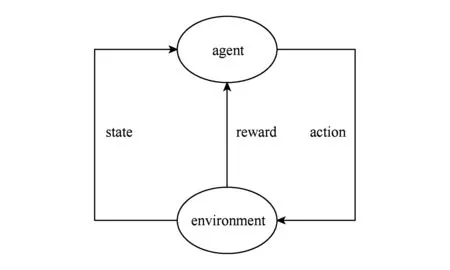
Fig. 1 The diagram of reinforcement learning framework图1 强化学习模型框架示意图

在强化学习中，可以使用状态动作值函数来评估策略.状态动作值函数Qh(x,u)是指依据策略h，在当前状态xt下执行动作ut，直到情节结束所获得的累积奖赏之和，Qh(x,u)可以表示为

Qh(x,u)=E[Rt|xt=x,ut=u,h],

(2)

其中，E表示期望.

状态动作值函数Qh(x,u)遵循贝尔曼方程.根据贝尔曼方程获得的时间步t+1的状态动作值Qt+1(x,u)为

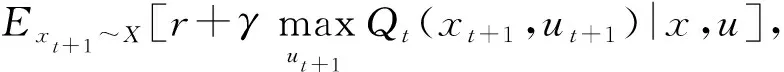
(3)

其中，Qt(x,u)是时间步t的状态动作值.利用贝尔曼方程不断迭代，状态动作值最终收敛，从而得到最优策略.

根据状态迁移函数P是否已知，强化学习可以分为基于模型的动态规划算法和基于无模型的强化学习算法；根据生成行为的策略和更新值函数是否相同，基于无模型的强化学习算法又分为同策略算法(on-policy)和异策略(off-policy)算法.深度Q网络方法所用到的Q-learning算法就是一种典型的异策略算法[15].Q-learning算法的更新公式为

(4)

Q(xt,ut)=Q(xt,ut)+αδ,

(5)

其中，γ为折扣因子，δ为TD-error.Q-learning算法所学到的动作值函数是直接逼近最优动作值函数而不依赖于其策略，简化了算法的分析.

1.2 深度学习

深度学习的基础是人工神经网络(artificial neural network, ANN)，由浅层学习发展而来.反向传播(back propagation, BP)算法[16]是深度学习的基本算法.利用反向传播算法可以让一个人工神经网络从大量训练样本中学习到数据的分布式特征，从而对未知样本进行预测.由多个隐藏层构成的多层感知器(multi-layer perceptron, MLP)比浅层网络特征表达的能力更强.

前馈网络是一种常见的神经网络连接方式.前馈深度神经网络在每一层使用函数将一批输入的集合传输到输出层，不断地调整网络参数，优化网络.卷积神经网络就是一种经典的前馈深度神经网络，通常包括卷积层、池化层和全连接层.卷积神经网络可以以图片等高维数据为直接输入，采用局部连接和共享权值的方式，减少了权值的数量，使得网络易于优化，也降低了过拟合的风险.Krizhevsky等人[17]提出的深度卷积神经网络使用非线性激活函数整流线性单元(rectified linear unit, ReLU)，加快了收敛速度并抑制了梯度消失问题.由于其采用纯粹的监督学习训练方式，代替了“预训练+微调”的方式，引起了基于卷积神经网络的深度学习研究热潮，如Simonyan等人[18]提出的模型进一步提高了图像的识别能力；He等人[19]提出了有152层深度的深度残差网络(deep residual network, DRN).

循环神经网络(recurrent neural network, RNN)隐藏层的结点有存储历史信息的功能，常被用于处理具有时序特性的问题[20].循环神经网络可以看成是一个共享同一参数的多层网络，然后再根据时间序列展开计算.虽然循环神经网络可以“记忆”历史信息，但是它难以保存相隔时间较长的信息.但是，循环神经网络存在梯度消失的不足.针对这些问题，研究人员提出了长短期记忆网络(long short-term memory, LSTM)和门限循环单元[21](gated recurrent unit, GRU)，弥补了循环神经网络存在的缺陷.此外，还有一些研究人员运用其他的机制来改进循环神经网络，如将结合注意力机制与循环神经网络，使得网络能记住历史信息中的关键部分[22].

1.3 深度Q网络

Mnih等人[9]在传统强化学习中的Q学习算法和深度卷积神经网络的基础上提出了深度Q网络，用于处理基于视觉的控制任务，缓解了用非线性函数逼近器表示值函数时算法的不稳定性.深度Q网络结构示意图如图2所示:

Fig. 2 The diagram of the architecture of deep Q network图2 深度Q网络结构示意图

深度Q网络的输入是已经被预处理的4幅84×84图片.第1层卷积层有32个8×8卷积核对图片进行卷积操作，卷积步幅为4；第2层卷积层有64个4×4的卷积核，卷积步幅为2；最后一层卷积层有64个3×3的卷积核，卷积步幅为1.每一层卷积层后都有1个非线性激活函数ReLU，在3层卷积层后跟着2个全连接层，第1个全连接层拥有512个结点，第2个全连接层的结点数与动作数量一致.

深度Q网络方法主要有2点改进:1)使用了经验回放方法，在每一个时间步t，agent将与环境交互产生的转移样本et=(xt,ut,rt,xt+1)存储到经验池Dt={e1,e2,…,et}中.采用等概率方式在经验池中抽取出相同数量的转移样本.经验回放方法可以打破样本之间的关联性，使深度Q网络能处理很多任务，如控制Atari 2600游戏.2)使用了2个网络来分别表示当前值函数和目标值函数，其中，采用实时方式更新当前值网络参数θ，而目标值网络参数θ-则在L步后通过复制当前值网络参数θ得到.在每一时间步t，通过不断减小目标值函数和当前值函数之间的均方误差来更新参数θ，损失函数为

(6)

进一步得到

(7)

式(7)并不需要计算所有的梯度，只要计算合适批量来优化损失函数.因此，可以选用随机梯度下降的方法来计算.网络参数根据损失函数梯度下降的方向调整

(8)

近年来，出现了以深度Q网络为基础的各种改进模型.针对强化学习算法Q-learning会出现乐观估计动作值的问题，Van Hasselt等人[23]在双Q学习算法(double Q-learning)[24]的基础上提出了深度双Q网络(double deep Q-network, DDQN).该方法在计算目标网络的Q值时使用了2套不同的参数，有效地避免了深度Q网络过高估计动作值的问题.深度Q网络通过采用重复4次相同动作减少动作选择以有利于下一个状态.Lakshminarayanan等人[25]根据当前状态重要性有所不同的特点，提出了动态跳帧的方法重复动作，有效地提高了模型的训练效果.Wang等人[26]将深度Q网络中卷积神经网络所提取的特征分为优势函数(advantage function)和与动作无关的状态值函数，使用这2个函数来生成状态值函数，提出了竞争深度Q网络(dueling deep Q-network， DuDQN)，在不改变底层强化学习算法的情况下进一步提高了深度Q网络的效果.

上述这些改进后的模型都是基于卷积神经网络的.从卷积神经网络的结构来看，每层神经元的信号只能向上一层传播，因此，如果不同时刻的子任务之间存在依赖关系，这些模型的效果表现就一般.Narasimhan等人[27]提出了深度循环Q网络(deep recurrent Q-network, DRQN)，首次引入了长短期记忆网络[28]，在处理一些带有时序性的文本任务中表现良好.在此基础上，Hausknecht等人[29]提出了深度循环Q学习算法(deep recurrent Q-learning, DRQ)，在处理部分可观测Markov决策过程(partially observable Markov decision process, POMDP)问题时取得了良好的效果.

2 基于最大置信上界采样的深度Q网络模型

2.1 基于最大置信上界采样

在深度Q网络中，等概率采样不能充分利用有价值的转移样本；而且在有限的经验池中，等概率采样存在重复采用低价值样本、遗漏重要样本等问题，导致学习效率低下.

在强化学习中，研究人员通常认为那些取得较大奖赏的动作可以加速模型的学习，因此，本文增加了选取具有较大奖赏的动作的概率.然而，随着选择较大奖赏动作的概率逐渐提高，选取其他动作的概率就会不断降低，这就有可能使算法陷入局部最优；而且这样做也无法保证样本多样性的要求.因此，亟需一种既可以充分利用大奖赏动作又能保证样本多样性的方法.

在强化学习中，由于动作值函数的估计值是未知的，因此需要进行适当的探索.贪心(greedy)方法选择当前状态下获得立即奖赏最多的动作.但是，贪心方法有可能会遗漏其他使得累积奖赏更大的动作.为了增加探索到未被发现的优秀动作的概率，常常使用ε-贪心方法选择动作.然而，ε-贪心方法未区分非贪心动作实际存在的重要性差异.Auer等人[14]提出了使用最大置信上界(UCB)思想解决多臂赌博机(multi-armed bandit)问题，在当前时刻选择最优动作和选择未来最优动作之间进行了优化，有效地平衡了探索和利用的关系.受到该方法的启发，针对经验重放方法所存在的问题，本文提出一种基于最大置信上界的优先级采样方法，通过提高奖赏较大的动作的被选概率，有效地增加了经验池中重要样本被采样的可能性；另一方面，通过提高未被选取样本的被选概率，保证了数据采样的多样性.本文将上述采样方法应用于深度Q网络，构建了一个基于最大置信上界采样的深度Q网络(upper confidence bound sampling deep Q-network, UCBS-DQN)，总体结构如图3所示.

Fig. 3 The diagram of the architecture of UCBS-DQN图3 UCBS-DQN结构示意图

在UCBS-DQN方法中，当前值网络的输入是经过灰度处理后的图片,这些图片经过网络的训练后得到当前动作值函数，与目标值网络中的最大动作值函数形成误差函数，使用基于均方根的传播方法(root mean square propagation, RMSProp)最小化误差函数；从经验回放单元提取经过处理后选择的样本，选择动作；每间隔L步(通常L取较大值)将当前值网络参数复制给目标值网络参数.图3中的虚线部分是本文的改进之处.在每一次执行动作后，计算样本的优先级并进行归一化操作，给经验池中的样本赋予优先级，更新网络所用样本通过样本特征抽取获得.从图3中可以看到，本文方法在从经验回放单元中抽取样本时利用最大置信上界的思想，用新的方法给样本赋予优先级.对于每个样本的选取概率更新公式为

(9)

(10)

式(9)中加入了样本选取的不确定估计机制.当第i个样本被选择后，由于Ni出现在平方根项的分母上，因此，该样本被选概率会随着时间步而逐渐降低.另一方面，随着训练的进行，时间步t逐渐增加，其他样本在之后时间步被选的概率也会提高.当第i个样本中的奖赏为正奖赏时，即可认为该样本为优秀样本.为了限制奖赏的影响力，且统一不同实验中奖赏的度量尺度，本文将正奖赏设置为1，负奖赏设置为-1.这样既提高了奖赏较大的样本被选概率，又降低了奖赏较低样本的出现概率.随着步数的增加，时间步t的影响会越来越大.为了减缓时间步t的增长速度，更新式(9)中使用了对数函数，使时间步的影响力小于样本获得奖赏大小的影响力.本文方法还考虑了信息量较大的样本以及未被选择的样本，保证了样本的多样性.

2.2 算法描述及分析

本文将基于最大置信上界的优先级采样应用于深度Q网络，得到了基于最大置信上界采样的深度Q学习方法，具体描述如算法1所示.

算法1. 基于最大置信上界采样的深度Q学习方法(UCBS-DQN).

① 初始化：经验回放单元D中的容量N;抽样样本数量minibatch的大小为32；每个样本初始概率pi=1N,i∈[1,N]；当前值网络的参数为θ，目标值网络的参数为θ-(θ=θ-)；选择随机动作概率为ε；i=0;时间步t=0.

② Repeat(对每一个情节)：

初始化并预处理状态序列φ1=φ(x1)；

③ Repeat(对于情节中的每个时间步)：

④ 用ε-贪心选择随机动作ui；

⑤ 执行动作ui，得到一幅图像oi+1和立即奖赏ri；

⑥ 设置xi+1=xi,ui,oi+1，并处理得到

φi+1=φ(xi+1)；

⑦ 将(φi,ui,ri,vi,φi+1)作为一个样本存储到D中；

⑧ Repeat(对每一个批次样本)：

⑨ 随机在[0,1]之间取值random()；

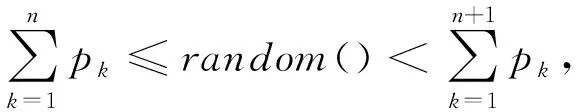
在算法1中，步⑨～⑩是基于最大置信上界采样算法采样的过程，通过优先级计算，每个样本的被选概率不同；步～是产生优先级的过程，根据样本的奖赏和被选次数设计优先级；步计算损失函数的梯度.

2.3 复杂度分析

UCBS-DQN方法大致可以分为优先级标签提取、计算优先级和模型求解3个阶段，下面从这3个角度分析模型复杂度.

1) 优先级标签提取阶段.在UCBS-DQN方法中，每一个情节中包含了若干时间步，在每个时间步中提取样本优先级标签以更新网络参数.当经验池容量满后不再变化，其大小为常数.每个训练批次提取样本的数量为32，因此，提取样本优先级时模型空间复杂度为O(1)，时间复杂度都为O(n).此外，在UCBS-DQN方法中，需要从经验池中抽取样本送入网络进行训练以更新参数，模型参数每隔L步更新一次且L取值较大(实验中L=10 000)，其余时刻大部分用于执行优先级更新操作，因此网络参数更新时间复杂度和空间复杂度都为O(1).

2) 计算优先级阶段.优先级的计算是在游戏每个执行动作之后，对经验池中样本优先级进行计算，在计算其优先级时需要遍历每一个样本，再由样本被选概率更新方式得到计算优先级的时间复杂度为O(n).由于样本上限为常数，因此其空间复杂度为O(1).

3) 模型求解阶段.整个模型需要重复执行M轮，因此，在模型求解阶段算法时间复杂度为O(n).

由于优先级标签提取、计算优先级和模型求解阶段是层层嵌套的，因此，整体而言，UCBS-DQN方法的算法时间复杂度为O(n3).

经过复杂度分析可知，本文提出的UCBS-DQN方法能够通过消耗较小的空间和时间代价得到经验池样本优先级，并通过其被选概率选择样本.

3 实验结果及分析

在本节中，首先介绍实验所用平台和实验中所用参数；随后，对深度Q网络(DQN)、深度循环Q网络(DRQN)、基于时间差分误差的优先经验回放(PER)以及本文提出的基于最大置信上界采样的深度Q学习方法(UCBS-DQN)在部分Atari 2600游戏中的表现进行评估；最后，结合实验结果和游戏特性分析UCBS-DQN方法的优势.

3.1 实验平台及实验介绍

OpenAI是一家非营利性的人工智能研究公司，创立初衷是预防人工智能的灾难性影响，同时为推动人工智能的发展发挥积极作用.OpenAI公司于2016年提出的Gym是一种用于开发和比较强化学习和深度强化学习算法的工具包，提供了各种Atari 2600游戏接口，包括策略类、动作类、桌游类、体育竞技类等59种经典游戏.Gym为人工智能研究人员提供了丰富且具有挑战性的深度强化学习平台.本文的实验环境基于Gym的Atari 2600游戏环境.

本文的实验比较了4种方法在4个Atari游戏中的效果，包括Seaquest游戏、Breakout游戏、Space Invader游戏和Assault游戏.1)Seaquest游戏是潜水艇对战游戏,其奖赏来自于潜水艇击杀潜艇类别和数量，若被其他潜艇子弹击中，则游戏结束.在游戏中，潜水艇每隔一定时间都需要在海底获得一个一次性的氧气瓶，然后浮出水面吸收氧气,当氧气瓶中的氧气耗尽时，游戏就结束.2)Breakout游戏是一种小球击打砖块的游戏,小球从下方开始击打上方的砖块，每成功击打一次就获得一个奖赏.击打的位置不同，所获得的奖赏也不同.通过控制屏幕底端的板块来反弹小球，防止小球掉落,若小球掉落则宣告游戏结束.3)Space Invader游戏是操控一架只能在一条水平线上的战斗机，消灭在画面中的敌方飞机.若我方战机被对方子弹打中，游戏就结束.4)在Assault游戏中，玩家操控飞机消灭源源不断产生的敌机，随着游戏的过程，敌机速度会越来越快，消灭飞机所获奖赏也会相应提高，若我方飞机被子弹击中，游戏就结束.

本文实验使用Intel i7-7820X处理器，使用GTX 1080Ti图形处理器对深度学习运算进行辅助加速计算.实验中，使用强化学习模型对Atari 2600游戏进行建模，其中，距离时间步t最近的N幅视频帧构成了状态xt=(st-N+1,st-N+2,…,st)∈X，agent从在动作集U中选择一个动作ut={1,2,…,K}∈U，执行后产生新的游戏画面代表agent转移到下一状态xt+1，2幅画面的得分差值即为奖赏rt.

3.2 参数设置

本文对比了DQN，DRQN，PER以及UCBS-DQN方法的性能.实验中，4种方法均采用RMSProp方法更新参数，其动量参数设置为0.95.

在Gym包中，各个游戏所获得的奖赏差异较大，这会影响到最终网络输出的Q值，进一步影响动作选择.为了缩小Q值的范围，实验中将所有大于1的奖赏设置为1，所有小于-1的奖赏设为-1，处于[-1,1]之间的奖赏值不变.此外，当前网络和目标网络之间的误差项也被控制在[-1,1]之间，这可以防止结果陷入局部最优，提高系统稳定性.

Gym提供的Atari 2600游戏图像像素是210×160.为了方便图像处理，将图像像素预处理为84×84的灰度图像，并以处理过后的4幅图像作为网络输入.训练时，如果一个动作仅执行一次，则会使得策略在空间和时间上变化太快，从而导致网络需要经常选择动作，而选择动作需要根据深度网络进行层层计算得到的结果来判断，造成深度网络计算所用时间远远大于网络前向传播的时间.因此，实验重复采取4次当前动作，这样既减少了计算量，又保持了动作序列的多样性.在实现经验回放方法时，由于初始状态的经验池缺乏样本数据，故而在实验的前50 000步对经验池进行填充.经验池的容量设置为最大存放100万个样本，每次从经验池中取出32个样本放入网络进行训练.Q值更新的折扣率γ设置为0.99.由于在训练后期，训练步幅过大可能会导致算法不收敛，而此时使用ε-贪心方法探索也足以满足需求，因此，实验中每隔100 000步以每次下降4%的步长进行衰减：网络更新参数α从0.005下降到0.000 25，ε-贪心策略的参数ε从1下降到0.1.

3.3 实验结果分析

在实验中，每种方法使用相同参数：采用500个训练阶段，每个训练阶段设置为10 000步.图4显示了各方法在4种不同游戏中所获得的平均奖赏.从图4中可以看出，UCBS-DQN方法的平均每情节奖赏高于其他3种方法.

从图4(a)中Seaquest游戏的平均奖赏图可以发现，面对这种复杂的环境，DQN和DRQN方法表现都不令人满意;PER方法虽然通过使用TD-error优先级提高了每情节奖赏，但需要经历240多个训练阶段之后才出现效果的提升;而UCBS-DQN方法在第100轮训练阶段的平均每情节奖赏就已经是DQN方法的5倍、DRQN方法的4倍，效果得到了大幅提升.经过分析可知，Seaquest游戏的上浮吸收氧气情节需要一直执行上浮动作，这些动作在当前阶段得到的反馈较差，但却是必须执行的.因此，DQN和DRQN方法中，这些动作对平均奖赏值的提高作用有限.使用了TD-error优先级的PER方法虽然比DQN和DRQN方法表现好，但该方法并不具备很好的探索其他训练样本的机制，导致了其效果需要在较多的训练阶段之后才能得到显著的提升.而UCBS-DQN方法增加了那些不常被选择的样本的被选概率，加之引入跳帧机制，使得潜水艇能够以大概率执行上浮动作，保持更长的游戏时间，提高了平均每情节奖赏.

Fig. 4 The average reward of different approaches in different Atari games图4 各方法在Atari游戏中的平均奖赏

从图4(b)中Breakout游戏的平均奖赏图可以发现，UCBS-DQN方法能更快地取得更好的效果，并且在训练过程中的每情节奖赏一直高于其他3种方法.但是，UCBS-DQN方法所获得的提升效果不如Seaquest游戏明显.这是因为Breakout游戏环境较为简单，其动作除去开局阶段的开球，在游戏过程中只有左右移动和静止，且其状态数量也少于其他游戏，这使得经验池中样本相似性增大.因此，UCBS-DQN方法使用未被选择的样本来训练，其提升效果就受到限制.而另一方面，由于Breakout游戏状态相似性较高，UCBS-DQN方法可以很快地找到较好的动作值函数，故而在训练到第100轮左右时就有很好的成绩，明显优于其他3种方法.

从图4(c)中Space Invader游戏的平均奖赏图可发现，UCBS-DQN方法较其他3种方法有显著的提高.在经历了500个训练阶段后，UCBS-DQN方法所获得的奖赏是DQN方法的3倍多、是DRQN方法的近4倍、是PER方法的2倍.而且可以看出，UCBS-DQN方法每阶段所获得的奖赏仍然处于一个上升的趋势.这是因为Space Invader游戏中敌机数量已知且位置变化范围不大，UCBS-DQN方法会以较高的概率选择那些取得高奖赏值的样本，因此，实验中UCBS-DQN方法所获得奖赏呈大幅上升趋势.

从图4(d)中Assault游戏的平均奖赏图可以发现，UCBS-DQN方法表现依然突出，且在500轮训练阶段后依然保持着上升趋势;虽然PER方法比DQN方法和DRQN方法好，但是，PER方法探索性能较差，很难发现未遇到的优秀样本，导致在经历了一段时间的提升后，PER方法中每情节所获得的奖赏难以持续提高.而由于UCBS-DQN方法具有较强的探索能力，可以发现更多的优秀动作，因此能保持良好的上升态势.

通过上述4个实验，可以得出UCBS-DQN方法取得效果显著时的条件：1)在环境中存在着较难被探索到的且奖赏值较高的样本，如Seaquest游戏环境中上浮获取氧气；2)环境中存在重复执行某个动作依然能获得较高奖赏的现象，如Space Invader游戏中击打飞机的情况.值得注意的是，UCBS-DQN方法并非仅仅简单地改变动作的被选概率来改善效果，而是考虑了更多的信息，通过对经验池中的元组进行选择，以元组中的状态(即经过处理的图像)为输入进行网络训练，采用ε-贪心方法选择动作，因此可以有效地降低陷入局部最优的可能.

损失函数的损失值是衡量算法收敛速度的一个重要标准.本文使用式(6)计算了4种方法在不同游戏中损失函数的损失值，如图5所示.

从图5中可以看出，每一种方法在刚开始训练时其损失值有一个上升的过程.而UCBS-DQN方法在短暂的上升之后，其损失值一直保持在一个非常低的状态.在Space Invader游戏和Assault游戏中，UCBS-DQN方法的损失值甚至持续降低，这是因为UCBS-DQN方法有较强的探索性，使得其能快速找到最优策略.

好的方法不仅应该在训练阶段表现出上佳性能，而且能使用已经训练好的模型进行实际控制操作.为此，本文进行了实战游戏测试.在测试过程中，agent使用训练好的模型，完全控制实战游戏，完成50 000步的测试，其中选择动作依然采用ε-贪心策略.在之前的测试阶段，通过选用ε-贪心策略来减少过拟合的可能，而此时模型已经训练完毕，因此，ε取较小数值，设为0.01.每个模型都进行20次独立的测试，每次测试后获得游戏每一个情节的平均奖赏、最大值、平均奖赏的方差和每50 000步可以运行的游戏轮数，如表1所示.

Fig. 5 The loss of different approaches in different games图5 各方法损失值比较图

GameApproachAverage rewardMaximal rewardVarianceRounds of gameBreakoutSeaquestSpace InvaderAssaultDQN2.8710.0 0.017900.2UCBS-DQN3.3520.00.014850.4DRQN2.8710.00.052513.5PER3.0412.00.021892.6DQN34.92200.03.18796.2UCBS-DQN150.45600.085.90472.8DRQN41.33120.07.16772.8PER129.86440.074.30487.2DQN116.54815.096.33547.5UCBS-DQN317.831195.0705.57350.8DRQN72.91500.02.19957.0PER162.66940.0169.30475.2DQN197.921302.0161.50327.6UCBS-DQN661.522142.03301.52178.4DRQN110.01525.068.95393.8PER411.831058.01065.28184.0

Notes: The bold values represent the maximum values in the average reward and maximal reward.

从表1中可以看出，UCBS-DQN方法在每情节所获得的平均奖赏上都有不同程度的提高.在最大值这项指标上，UCBS-DQN方法的表现依然优于其他方法.此外，UCBS-DQN方法在固定50 000步所获得平均游戏轮数最少，说明其在平均每轮游戏中存活步数最长，训练较为成功.

4 结束语

深度Q网络及其相关改进方法在Atari游戏中有着很好的表现，证明可以较好地解决一些视觉感知类问题.然而，对于战略性任务这些模型效果提高有限，主要原因在于环境中存在着需要长时间步才能表现出优秀的状态.本文提出了一种基于最大置信上界采样的UCBS-DQN方法，该方法通过对经验池进行优先级采样，可以有效地探索未知状态，提高选择优秀状态概率，在很大程度上能够避免出现探索不到延迟奖赏的问题.本文通过4个Atari 2006实验验证了UCBS-DQN方法的有效性.

然而，从实验结果中可以发现，DQN,DRQN,PER和UCBS-DQN这4种方法的稳定性都不佳.因此，在如何提高模型稳定性方面仍有工作可以继续开展，可以采用监督学习方法或经验来协助训练出模型初始参数，然后再使用强化学习来更新策略.

ZhuFei, born in 1978. PhD and associate professor. Member of CCF. His main research interests include reinforcement learning, text mining and bioinformatics.

WuWen, born in 1994. Postgraduate of Soochow University. His main research interests include deep reinforcement learning and intelligence information processing (20164227051@stu.suda.edu.cn).

LiuQuan, born in 1969. PhD and professor. Member of CCF. His main research interests include reinforcement learning, and automated reasoning (quanliu@suda.edu.cn).

FuYuchen, born in 1968. PhD and professor. Member of CCF. His main research interests include reinforcement learning, intelligence information processing and deep Web (yuchenfu@cslg.edu.cn).