基于网络节点中心性度量的重叠社区发现算法

杜航原 王文剑 白 亮

1(山西大学计算机与信息技术学院 太原 030006)2 (计算智能与中文信息处理教育部重点实验室(山西大学) 太原 030006) (duhangyuan@sxu.edu.cn)

网络结构作为一种灵活普适的抽象和描述方式，能够对现实世界中大量复杂系统进行建模分析，例如，社会网络、蛋白质互作用网络、计算机因特网、生物疾病传播网络等都以网络形式呈现[1].在这些网络中，各个实体被抽象为网络节点，实体间关系被抽象为节点间的连边，这些网络结构具有较高的复杂性，被称为复杂网络[2-3].随着信息技术的快速发展，复杂网络已经逐渐成为人类生产生活密不可分的重要组成部分，关于复杂网络内部连接模式和结构特性的研究探索对人们深入了解和控制复杂系统具有重要意义.随着研究的深入，人们发现复杂网络的拓扑结构表现出一种社团化特征，即整个网络由若干社区结构组成，这些社区内部连接相对紧密，社区之间连接相对稀疏.网络社区结构是现实世界实体关系的一种映射，并广泛存在于各种网络中.有效发现网络中的社区结构对于分析复杂系统组成结构、了解系统内部互作用机制、揭示系统发展规律以及预测复杂系统行为具有重要的理论意义和实用价值[3-8].

近年来，网络社区发现问题不仅成为了计算机领域中一个极具挑战的基础研究课题，也吸引了大量来自物理、生物、医学和社会学等诸多领域研究人员的目光，成为一个热门的多学科交叉课题.发展至今，针对这一问题已经形成了大量具有代表性的算法，大致可分为4类：1)基于层次聚类的社区发现算法，通过度量网络节点间的相似度，进而将相似度较大的节点归为同一社区，将相似度较小的节点置于不同社区，根据其网络节点的聚类规则可分为凝聚式[9-10]和分裂式2类方法[11-12];2)基于优化模型的社区发现算法，模拟一个物理系统到达均衡状态的过程，定义一个目标函数度量社区划分结果的优劣[13-14]，在搜索空间中寻找使目标函数取得最优值的划分结果，其中最典型的度量函数是模块度[15];3)基于图分割的社区发现算法，其基本思想是根据网络Laplacian矩阵的特征向量分量对网络节点间的相似性进行度量，并利用其可以在任意形状样本空间上实现聚类的优点对网络社区进行划分[16-17];4)以直观或经验构造为基础的启发式方法也对社区发现问题的研究产生了积极意义，比较有代表性的方法主要包括标签传播算法[18-19]、基于距离或吸引力的算法[20-21]以及群智能算法[22-23]等.

在真实复杂网络中，往往存在一些节点属于多个社区的情况，即社区间存在彼此重叠的关系而非彼此独立，这类社区结构被称为重叠社区[1,7,24].例如，一个学者可能加入多个学术团体，一篇学术论文可能涉及多个主题，一个作者也可能参与多篇论文的发表，这些客观现象都导致了重叠社区结构的出现.在这种情况下，从复杂网络中发现具有重叠结构的社区往往具有更加重要的实际价值.

本文的主要贡献有4方面:

1) 提出了网络空间中节点的内聚度和分离度度量，用于描述网络社区内部稠密以及外部稀疏的本质结构特征，并基于上述特征计算节点中心度，对节点关于其所属社区的影响力进行分析;

2) 提出了基于节点中心度的网络社区中心的快速选择方法，能够在缺乏先验信息的情况下识别出网络中潜在的社区中心;

3) 利用节点关于网络社区的隶属度表达社区结构间的重叠特性，设计了非中心节点的隶属度迭代计算方法，将各节点分配到其可能隶属的网络社区;

4) 在人工网络和真实网络上的实验结果表明,本文提出的网络社区发现算法能有效发现复杂网络中存在的重叠社区结构.

1 相关工作

1.1 重叠社区发现

由于重叠社区结构中某些网络节点关于社区的隶属关系是重叠的，经典的面向独立社区的硬划分发现算法不再适用.因此，对重叠社区结构发现问题的研究逐步成为一个热点，经过近几年发展，在这一领域出现了大量相关研究成果.这些方法大体可分为：派系过滤(clique percolation method, CPM)算法、局部扩展算法、模糊发现算法、边划分发现算法和标签传播算法等5类[24].派系过滤算法最早由Palla等人[25]提出，其基本思想是构建由k个节点组成的完全连通子图(即k-派系)，通过搜索具有k-1个相同节点的邻接派系实现重叠社区的发现.文献[26]将CPM算法拓展到有权网络，在对k-派系进行搜索时引入了子图密度的概念，通过设置阈值有选择地将k-派系加入社区.文献[27]将网络节点分为孤立节点、重叠节点和连接节点，首先基于深度和广度搜索抽取网络中的最大派系，接着利用指定规则将最大派系两两融合扩展为更大的子图，再利用模块度判定社区划分的质量，该方法能成功地识别出网络社区之间的重叠节点和连接节点.Zhang等人[28]依据耦合强度这一目标函数对网络中搜索到的派系进行合并，再对得到的树状图进行层次划分获得重叠社区结构.这类方法以派系为单位检测社区的重叠性，在处理稀疏网络社区发现问题时效果不够理想，而且算法的时间复杂度相对较高.

局部扩展算法的基本思想是，依据某种策略在网络中搜索种子节点，再通过一个局部优化函数对种子节点进行扩展，最终获得社区的最优划分[29].例如，LFM 算法[30]结合适应度函数将节点连接形成社区，再以迭代过程选取社区外的节点为种子节点进行社区扩展.对于这种使用种子节点发现重叠社区的局部优化方法，如何选择适当的种子节点尤为重要，为此，Yang等人[31]设计了一种种子节点选择策略，首先利用节点连接密度将原始网络转换为一个有权网络，接着利用Prim或Kruskal 算法找到节点间的强连接抽取最大生成树，进而选取生成树中权重较大的节点作为种子，并基于PageRank值和模块度定义目标函数进行社区初始化，最后通过控制重叠率完成社区优化.文献[32]按照节点的度中心性从网络中选取种子节点，并依次计算每个种子节点与其邻居节点的局部簇系数，将这一系数作为对邻居节点合并的依据，从而完成社区结构的发现.局部扩展社区发现算法对种子节点的选取具有较大随机性，且对社区扩展的目标函数质量依赖较强，容易导致算法稳定性下降.

模糊发现算法利用隶属度表示节点和社区之间的隶属关系，将社区发现问题转化为确定节点隶属度的过程.文献[5]面向在线社交网络提出了一种基于模糊自适应推理理论的重叠社区发现算法，包含比较和预测2个阶段，在比较阶段通过节点的边介数和介中心度识别网络中的独立社区，在预测阶段利用对偶介数和介中心度进行重叠社区的初始化，通过2个阶段的循环迭代能较好地解决社区发现中产生的可塑性-稳定性问题.文献[7]提出了一种模糊模块度最大化(fuzzy modularity maximization, FMM)方法，利用模块度优化模型确定节点的最优隶属度，并设计了2种求解方法.此外，一些学者以非负矩阵分解为工具，提出了一系列节点隶属度的求解方法[6,24,33].模糊重叠社区发现算法的缺点在于，通常需要事先指定网络中的社区数量，这对于结构复杂的网络往往是不现实的.

以上算法在发现重叠社区结构时集中于对节点与社区关系的研究，与此不同，边划分发现算法从边的角度构建社区结构.Li等人[34]设计了一种以线图模型为基础的加权模型，基于链路聚类构成具有相似结构的链路社区，对模块密度函数进行优化识别出线图模型上连接稠密的链路组，并设计了一种新的基因表示模型将链路社区映射为节点社区，实现重叠社区的划分.Ahn等人[35]认为社区是网络中边的聚合，当几条边隶属不同社区时，它们的共有节点便成为了重叠节点，通过度量两条边之间的相似性对边进行层次聚类，能有效表达社区内节点的层次关系和重叠关系.文献[36]提出了一种社会网络的多尺度重叠社区发现算法，该方法利用边的局部集合对节点进行描述，分别在个体节点、个体连边和整个网络3个尺度上定义了社区结构应满足的定量标准，并设计了一种基于原型的社区发现算法，能够在大规模低密度网络上产生较好效果.目前，边划分发现算法已经成为一类重要的重叠社区发现算法.

基于标签传播的方法为每个网络节点分配包含重叠隶属关系的标签，通过这些标签在邻居节点之间的传播使节点关于各社区的隶属关系最终达到稳定状态，从而获得社区发现结果.这类方法的典型代表是基于多标签的COPRA算法和基于Speaker-listener模型的SLPA算法[24].Gaiter等人[18]于2015年提出了一种SpeakEasy聚类方法，利用自顶向下和自底向上2种策略识别社区，根据节点的局部连接性和网络结构的全局信息将节点加入社区，该方法能对社区结构稳定性做出定量评价，在10万级节点数量的网络中取得了较好效果.

1.2 密度峰值聚类

2014年Rodriguez等人[37]提出了密度峰值聚类算法，其基本思想是：簇中心被一些具有较低局部密度的节点围绕，并且距离其他高密度节点的距离较远.该方法依据节点间距离定义节点分布的局部密度，通过快速搜索和发现密度峰值进行聚类中心的选择，实现簇的划分.算法为每个节点定义了如式(1)所示的局部密度：

(1)

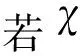
(2)

算法利用决策图搜索δi值异常大的节点作为簇中心，再将非中心节点分配到比其密度高并且距离最近的节点所属的簇中，实现对数据的聚类.

密度峰值聚类思想很适合用来描述网络社区内部稠密、外部稀疏的结构特征，因此一些学者[38-39]将密度峰值的概念用于重叠社区发现，为这一问题的研究开辟了新的方向.但这些方法存在一些共性问题，例如需要事先指定社区数量、需要设置节点间的截断距离、在度量节点间距离时将整个网络作为搜索空间引入了过高的计算量、难以应用于大规模网络等.为了解决这些问题，本文基于密度峰值聚类思想提出了一种面向重叠社区结构的自适应发现算法，利用网络节点的内聚度和分离度度量描述社区内部稠密、外部稀疏的结构特征，通过节点中心度反映节点对所属社区结构的影响力，在此基础上设计了社区中心的快速选取策略，最终确定各非中心节点的隶属度实现重叠社区结构的划分.该方法能获得接近真实社区划分的发现结果，无需事先指定社区数量，具有较低的计算复杂度.人工网络和真实网络上的仿真实验结果验证了该方法的有效性.

2 基于节点中心度的重叠社区发现算法

在聚类问题中，节点的局部密度基于节点间距离进行定义，而网络中的节点并非定义在几何特征空间中，我们能获得的仅仅是网络节点间的连接关系，基于距离对节点局部密度进行定义不再适用，并且对于重叠社区，节点与社区的隶属关系相比独立社区更加复杂.为此，本文利用节点间的连接关系定义了节点的内聚度和分离度分别用于描述社区内部连接的紧密性以及社区外部连接的稀疏性，在此基础上计算节点中心度替代局部密度，作为度量节点对社区结构影响力的重要性指标.

2.1 节点内聚度

为叙述简便，本文算法以无权网络为例进行阐述，对有权网络同样适用.对于一个以图G=V,E表示的复杂网络，其中V={v1,v2,…vn}为由网络中全部节点构成的集合，E={e1,e2,…,em}为节点间连边构成的集合.令NGi={vj|vi,vj∈E}表示节点vi的邻居节点构成的集合，则节点vi的度可表示为di=|NGi|.An×n=(ai j)为网络的邻接矩阵，若节点vi与节点vj存在连边，则ai j=1，否则ai j=0.

对于一个网络社区，其中心节点作为社区的组织和领导者，应该与其他节点保持比较密切的连接关系，因此中心节点通常具有较高的度.同时，社区内部的连接关系应该具有较高的相似性，即由中心节点关联的节点间具有较为相似的连接关系.基于这一假设，我们为网络节点的内聚度进行如下定义：

定义1. 网络节点内聚度.网络中节点vi的内聚度是该节点的度及其与邻居节点的最大相似度的乘积，可形式化表示为

(3)

其中Ii为节点vi的内聚度;simi,j=|NGi∩NGj|为节点vi与其邻居节点vj的相似度，即两节点共有的邻居节点数量.由这一定义可以看出，节点内聚度同时考虑了节点的连接数量和连接相似性2个因素，节点的内聚度越高，该节点对于社区内其他节点的聚合能力越强，这反映了社区结构内部连接的稠密性.

2.2 节点分离度

依据网络社区的定义，社区外部的连接是相对稀疏的，也就是说作为社区领导者的中心节点之间应该具有较低的相似性和连接密切性.根据节点内聚度定义可知，社区中心具有较高的内聚度，那么社区中心与其他内聚度较高的节点(潜在的社区中心)应该具有较低的相似性.基于这一思想，我们定义节点的分离度如下：

定义2. 网络节点分离度.网络中节点vi的分离度是内聚度比该节点高的节点与该节点间的最大相似度的倒数，可形式化表示为

(4)

其中，Pi为节点vi的分离度，其取值越大表明vi与内聚度更大的节点之间的相似性越低，这反映了社区结构外部连接的稀疏性.为了确保式(4)是有意义的，对分母进行修正，如式(5)所示：

(5)

2.3 社区中心的快速选择方法

基于密度峰值聚类方法的思想，我们认为社区中心是这样一些节点：1)在局部范围内具有较高的内聚度；2)与其他内聚度较高的节点间相似性较低.节点对这2个条件的满足程度越高，表明它对社区结构的影响力越大，也就越有可能成为社区中心.为此，我们利用节点的中心度描述其影响力.

定义3. 网络节点中心度.网络中节点vi的中心度是该节点内聚度与分离度的乘积，可形式化地表示为

Ri=Ii×Pi，

(6)

其中，Ri为节点vi的中心度，反映了节点对社区结构的影响力，中心度越高，则该节点越可能成为社区中心.

这样，我们可以获得每个网络节点的内聚度、分离度以及中心度.如果已知网络中社区数量K，则可直接选取中心度最大的K个节点作为社区中心.然而在很多实际网络中，我们很难预先获得准确的社区数量，针对这一问题，本文提出了一种能够快速确定社区中心的方法.

首先，利用式(7)求取各节点中心度的Z分数(Z-scores)：

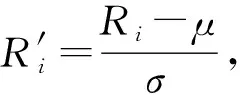
(7)

其中，

(8)

(9)

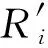
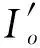
算法1. 社区中心自适应选择算法.

输入：复杂网络G=V,E、邻接矩阵An×n；

输出：社区中心节点集合C.

① for each nodevi∈V

② 通过式(3),(5),(6)分别计算节点vi的内聚度Ii、分离度Pi以及中心度Ri；

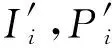
④ end for

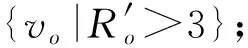
⑦ returnC={ck}.

2.4 节点的社区分配

本文通过隶属度向量表示节点关于各社区的隶属情况，假设网络中包含K个社区，则节点vi的隶属度向量可表示为ωi=(ωi,1,ωi,2,…,ωi,K)，其中ωi,k为vi关于第k个社区的隶属度.通常情况下社区中心不会成为重叠节点，因此社区中心ck关于第k个社区的隶属度设置如下：

ωcj,k=Δcj,k，

(10)

其中，

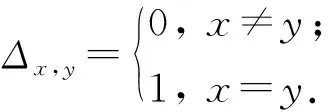
(11)

非社区中心节点的隶属度向量依赖于比其内聚度更高的节点，并且二者之间的相似度越高，这种依赖关系越强烈.为便于计算，我们将网络中所有节点按照内聚度进行降序排列，得到的节点列表V中任意2个节点vp和vq满足若pvq.此外，依据节点中心度定义可知R1=maxRi.各非中心节点的隶属度向量可通过式(12)依次计算：

(12)

其中，

(13)

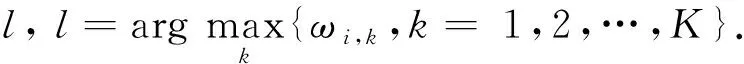
算法2. 节点社区分配算法.

输入：社区中心节点集合C、按内聚度降序排列的节点列表V、节点中心度Ri、阈值θ；

输出：节点隶属度向量ωi.

① for each core nodeci∈C

② for each communityk=1,2,…,K

③ ifci是第k个社区的中心；

④ωi,k=1;

⑤ else

⑥ωi,k=0;

⑦ end if

⑧ end for

⑨ end for

⑩ for each non-core nodevi∈V-C

3 实验与结果分析

为验证算法有效性，我们选取LFM[29],LINK[35],COPRA[24],OCDDP[39]以及CFinder[40]等重叠社区发现算法与本文提出方法进行实验比较.实验环境为：处理器Inter Core i7 4790 3.60 GHz，内存8 GB，操作系统Windows10 64 bit.

3.1 实验数据集

本文分别利用人工网络数据集和真实网络数据集对多种算法开展实验分析与比较，其中真实数据集选取如表1所示的8个常见网络数据集，人工数据集由LFR基准生成.

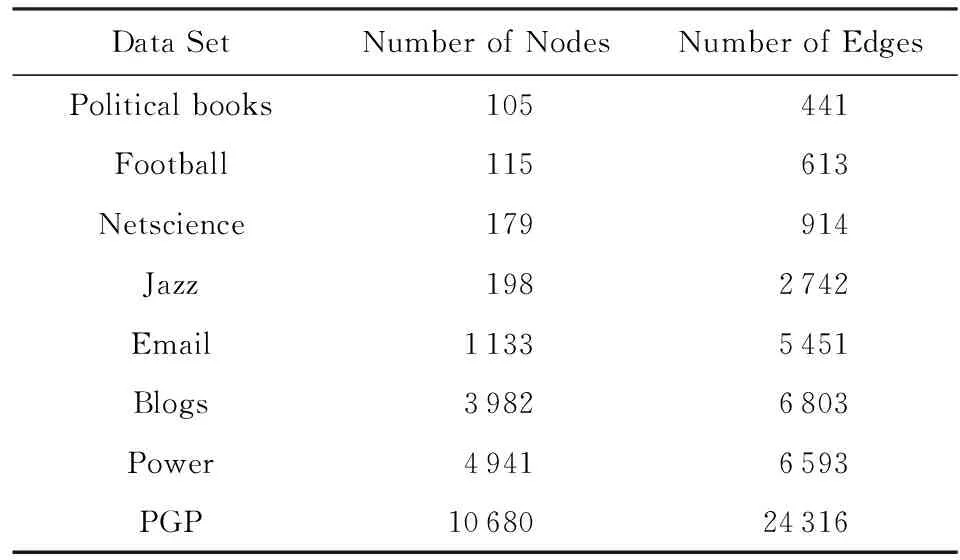
Table 1 The Real Network Dataset表1 真实网络数据集

LFR基准网络能对真实网络的特性进行较好的模拟，例如节点度和社区大小的无标度性等，且其社区结构特性通过参数指定，便于对社区发现质量进行客观评价，是当前网络社区发现研究中常用的人工数据集.LFR基准网络的结构特性由表2所示参数指定：

Table 2 Parameters of LFR Network表2 LFR网络参数

3.2 评价准则

1) 人工网络评价准则

对于由LFR基准生成的人工网络，其网络特性通过多个参数进行指定，社区结构真值已知，可利用标准化互信息(normalized mutual information,NMI)[16]作为各社区发现算法的评价指标.NMI指数通过信息熵定义，用于反映社区发现结果与真实社区划分之间的相似程度，取值范围为0≤NMI≤1，其取值越高，表明社区发现结果越接近真实值.

2) 真实网络评价准则

对于真实网络，由于缺乏社区结构的先验真值，一般利用模块度将社区划分后的网络与相应一阶零模型网络进行比较，以此评价社区发现结果的质量.由于模块度函数Q假设各社区之间相互独立，只适用于独立社区评价，为此本文选取2类重叠模块度函数Qov[24]和EQ[41]作为算法发现结果的评价指标.这2种模块度函数是在重叠社区结构下对模块度函数Q进行扩展，其取值越大，表明社区发现结果的质量越高.

3.3 人工网络实验结果

1)算法时间效率比较

我们利用LFR基准生成10个人工网络，用于测试和比较各种社区发现算法的运行时间，在这些网络中，节点数量依次设置为N=10 000～100 000，其他参数取相同值，d=15，dmax=50，γ=-2，β=-1，minc=10，maxc=500，mu=0.1，On=100，Om=3.

各社区发现算法在不同规模的人工网络上运行时间如图1所示.由图1可以看出，CFinder算法运行时间显著高于其他算法，当网络节点数量超过50 000后算法失效，这是由于算法以派系为单位检测社区的重叠性，派系的产生过程计算量较大；其他算法的运行时间与网络节点数量基本呈线性关系；LFM算法基于适应度函数局部最优化思想，在实验中取得了最高的计算效率；COPRA算法的计算量与迭代次数相关，因此当网络规模较大时，其算法计算效率有所下降； OCDDP算法基于节点间连接强度定义节点密度和距离，由于考虑到两节点间的间接连接方式，需要在整个网络上进行全局搜索，算法计算量对网络规模比较敏感；LINK算法在处理规模不大的网络时具有较高的计算效率，但由于其将所有的边都划分到特定的链接社区中，需要耗费较多的存储时间，当网络规模较大时，其计算量有明显增加；本文算法是对数据集的“一次性”扫描，计算量与网络规模呈线性关系，计算效率较高，且非常稳定.综上，本文算法在这些人工网络中的计算效率略低于LFM算法，但相比COPRA,LINK,CFinder和OCDDP等算法具有一定优势.

Fig. 1 Execution time comparison for different algorithms图1 各算法运行时间比较

2) 参数δ和θ的影响

为分析参数δ和θ对本文算法社区发现结果产生的影响，我们令δ的取值分别为2,3,4,5,6，以及θ的取值分别为0.5,0.6,0.7,0.8,0.9,1，在前述10个LFR人工网络上进行实验，取每一组参数设置下算法社区发现结果的NMI均值作为最终结果.这2个参数取不同值时算法获得的NMI值如图2所示，其中每条折线表示了给定δ取值算法社区发现结果随δ取值的变化情况.由图2可以看出，δ取3和4时，本文算法能获得较好的社区发现结果，而该参数取值为5和6时社区发现准确度较差，这主要是由于参数δ用于控制内聚度和分离度的相对关系，确保选择出内聚度和分离度都较大的节点作为社区中心，参数取值过小或过大都无法实现这一目的.参数θ的取值为0.8和0.9时，算法能获得较高的NMI值，这是由于算法首先考虑将非中心节点分配到使节点隶属度最大的社区，若节点同时作为2个社区的重叠节点，则节点关于这2个社区的隶属度应当较为接近；而参数θ的取值较小时，算法会将一些独立节点误判为重叠节点，导致识别出的社区结构过度重叠.

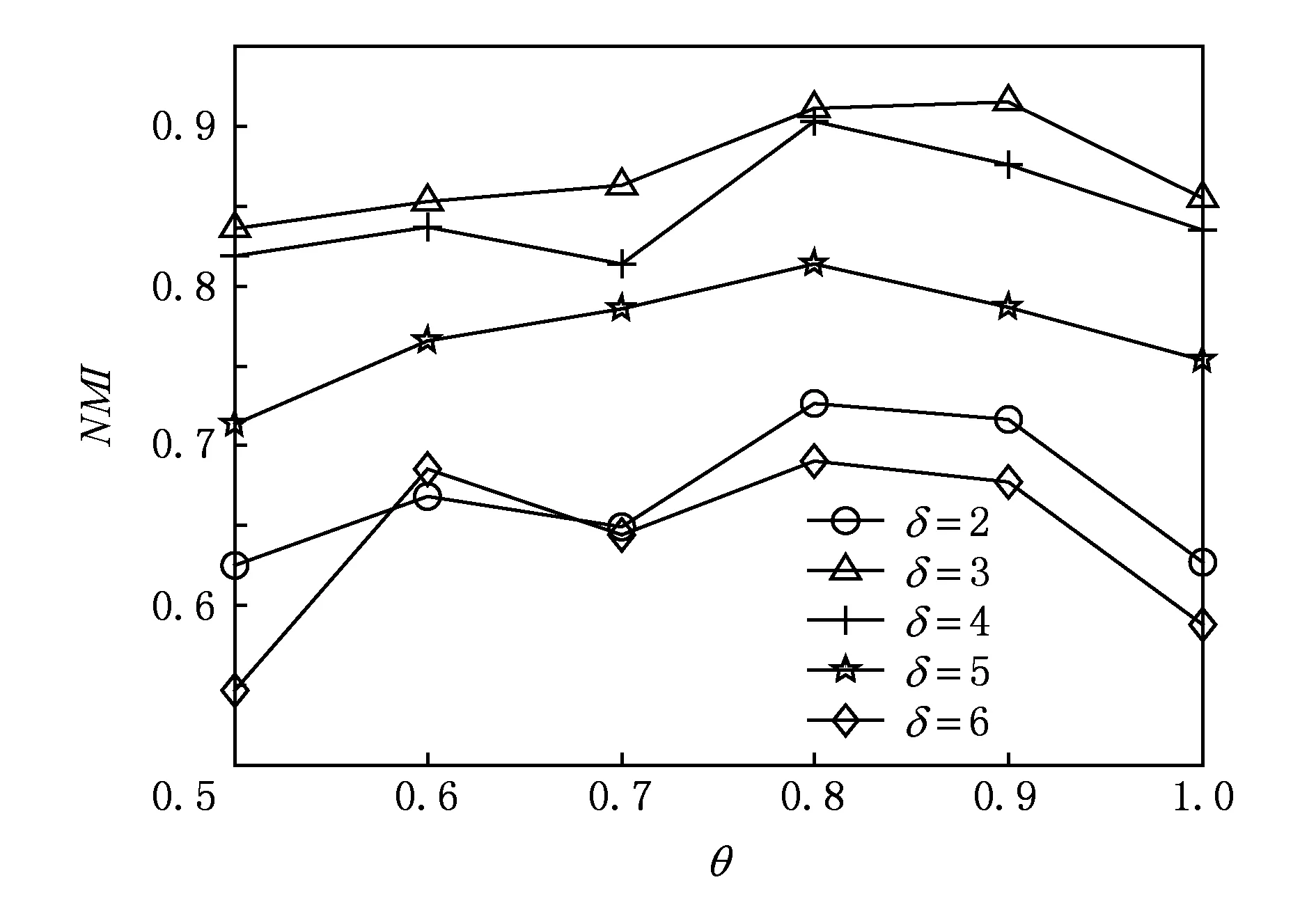
Fig. 2 Comparison results for parameters δ and θ图2 参数δ和θ取不同值时的结果比较

3) 各算法社区发现结果比较

为比较各算法在人工数据集上获得的社区发现精度，我们利用LFR基准生成8组网络数据，每组数据由8个网络构成，这些网络的Om参数取值分别为2～9，其余参数在每一组数据中使用相同的设置，如表3所示.用于对比实验的算法中LINK算法无需设置参数，其余算法的参数设置如表4所示.其中，LFM算法的参数α用于控制社区规模，COPRA算法的参数v表示节点携带的最大标签数，CFinder算法的参数k表示完全连通子图规模，OCDDP算法中的参数t和σ分别表示节点连接强度中绝对连接的权重以及节点关于重叠社区的分配阈值，本文算法中参数δ和θ分别用于控制节点内聚度与分离度的相对关系以及节点重叠程度.每种算法选取不同参数设置下的最大NMI值作为该算法运行结果，在各组网络中算法的社区发现结果如图3所示，其中横坐标为LFR基准的参数Om，纵坐标表示算法获得的NMI值.

Table 3 Parameter Settings of LFR Benchmarks表3 LFR基准网络参数设置

Table 4 Parameter Settings of Different Algorithms表4 各算法参数设置参数

Fig. 3 Community detection results of different algorithms on synthetic networks图3 人工网络上各算法的社区发现结果

与LFM算法相比，本文算法在混合度较低的网络上获得了与LFM算法相近的社区发现质量，2种算法的社区发现结果质量都较高，而对于混合度较高的网络，本文算法在大多数情况下能获得优于LFM的发现结果，表明本文算法在复杂网络结构中的重叠社区识别能力优于LFM.此外，重叠节点数量的变化对2种算法社区发现结果影响都不大，说明二者都具有一定的发现重叠度较高的网络社区的能力.

与LINK算法相比，本文算法在各个网络上都获得了更高的NMI值，这主要是由于LINK算法将所有边都视为重叠社区的一部分，容易导致社区结构过度重叠，使得社区发现质量降低；而本文算法对重叠节点的处理更加合理，仅选择相对隶属度较大的有效节点转化为重叠节点.

与COPRA算法相比，本文算法在所有混合度较低(mu=0.1)的网络中能够获得NMI值更高的社区发现结果，并且对于混合度较高的(mu=0.3)网络，算法在大部分时候仍然取得了更好的结果.而COPRA仅在个别网络中，如G4的Om=7和G6的Om=2时获得优于本文算法的结果.此外，随着Om取值的增大，在各组网络中社区发现的难度也随之增大，本文算法获得的NMI值整体呈现出较为平稳的下降趋势；而COPRA获得的结果出现了多次震荡，尤其是对于高混合网络，算法的稳定性较差.这主要是由于COPRA算法中存在较多随机因素，尤其是在更新标签和隶属系数时，往往需要对多余标签做随机删除，导致 COPRA算法得到的结果不够稳定.

与CFinder算法相比，本文算法在各个网络中获得的社区发现结果都优于CFinder，尤其是当网络mu参数较大时，本文算法能获得比CFinder更加稳定的社区发现结果.这主要是由于CFinder对mu参数容忍度较差，基本无法处理较为稠密的网络.

与OCDDP算法相比，本文算法同样基于密度峰值聚类思想，二者不同之处在于：OCDDP算法仅考虑节点的连接强度作为距离和密度度量，忽略了节点间连接关系的相似性对社区构成的影响因素，而本文算法通过内聚度和分离度能较好地反映社区内部稠密、外部稀疏的本质属性，因此在大部分网络中能够获得更好的社区发现结果.

综上，在不同人工网络中本文算法获得了优于其他算法的重叠社区结构发现结果.

3.4 真实网络实验结果

在表1所示的真实网络上，我们对各种重叠社区发现算法的结果进行比较，各算法仍采用表4所示的参数设置.对于LINK算法，我们设置参数c作为其将链接社区转化为节点社区时的最小边数量，令c的取值范围为2～15.各算法分别选取不同参数下最优Qov和EQ作为最终结果，表5给出了各算法在真实网络上的社区发现结果及最优参数值，并且将每个网络中社区发现结果的最大Qov值进行标黑.通过对比这些结果可以发现，LINK算法的社区发现Qov值是最低的，且这一算法的最大Qov值都是在参数c>0的不同值时获得的，说明算法构造的较小的链路社区影响了社区发现结果，简单地舍去这些小规模链路社区仍然无法显著改善算法有效性.在这些真实网络中，本文算法在大部分情况下都取得了最高的Qov值，并在Netscience和PGP网络中获得了非常接近最优值的次优结果.总体上来看，本文算法能够在各种真实网络中获得优于其他算法的重叠社区发现结果.此外，本文算法在不同网络上获得最大Qov值时对应的参数δ和θ取值变化不大，表明这2个参数的最优值具有较高的普遍适用性.

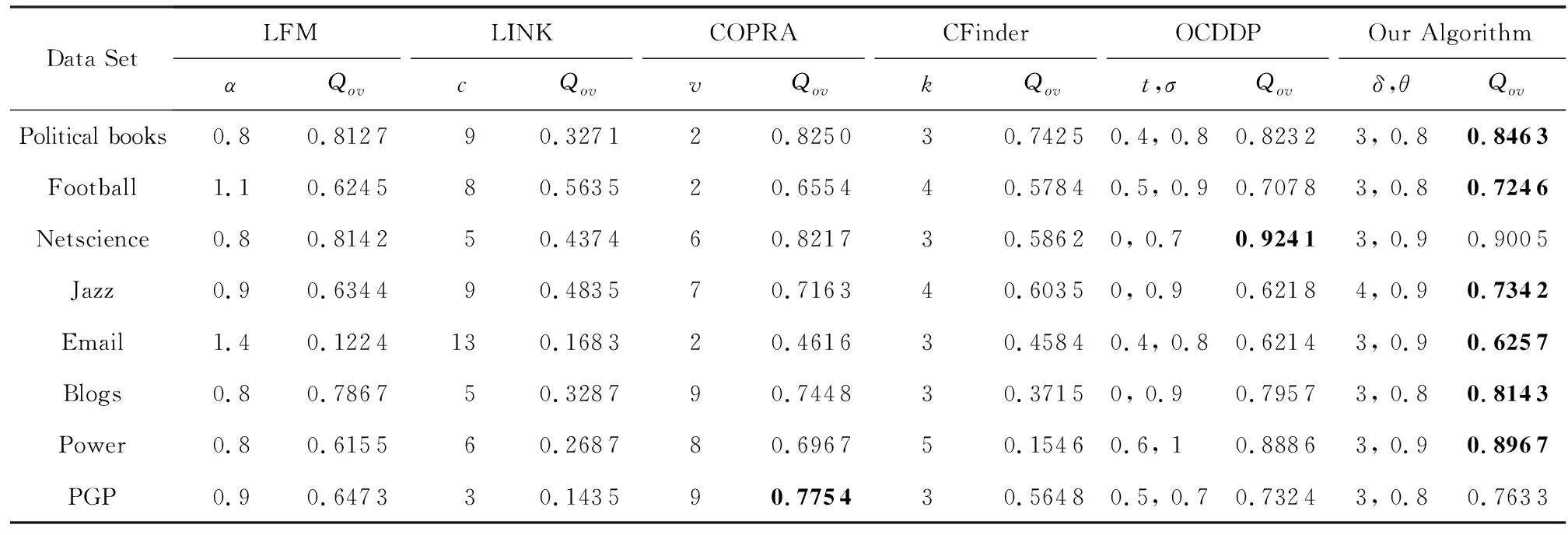
Table 5 Community Detection Results of Different Algorithms on Real Networks表5 网络上各算法的社区发现结果

4 总 结

本文设计了一种网络节点的中心性度量模型，基于网络社区内部连接稠密和外部连接稀疏的结构特征评价网络节点对所属社区的影响力，为网络节点中心性定量分析提供了有效途径.在此基础上，给出了社区中心节点的快速选择方法以及非中心节点的社区分配策略，提出一种基于节点中心性度量的重叠社区结构发现算法.在仿真实验中，利用人工网络和真实网络对算法的有效性进行了验证，实验结果表明，本文提出的重叠社区发现算法在社区发现质量和计算效率方面优于许多已有算法.在未来工作中，我们将在时空轨迹网络上对节点中心性度量模型及重叠社区发现算法开展探索应用，针对行人、车辆、飞机及船只等移动物体产生的大规模时空网络数据进行模式发现和异常检测分析.

DuHangyuan, born in 1985. PhD, master supervisor. Member of CCF. His main research interests include clustering analysis and complex network theory.

WangWenjian, born in 1968. PhD, professor, PhD supervisor. Senior member of CCF. Her main research interests include computational intelligence, machine learning, and machine vision.

BaiLiang, born in 1982. PhD, associate professor, master supervisor. Member of CCF. His main research interests include clustering ensemble and complex network theory.