中低压配电网系统的无功补偿装置的研究
张丽珍 王娟平
(山西电力职业技术学院电力工程系)
0 引言
电能质量问题的提出由来已久,而衡量电能质量的指标随着电力事业的发展得到人们的关注。在早期,电力负荷的组成都比较简单,20世纪80年代以来,越来越多的非线性电力电子器件和装置在现在的企业中得到了广泛的应用,使配电网无功补偿电压严重降低。电压降低给企业带来很大的不利,电压降低使电能在生产、传输和利用的过程中效率降低,不仅导致电能损耗增加和设备寿命缩短,使系统的功率因数降低;还会干扰保护继电器、测量设备、控制和通讯电路以及用户的电子设备等等,使灵敏的设备误动或元件故障,影响电网的可靠性。因此,随着全社会环保意识的加强,对配电网无功补偿的研究己成为国内外学者们所必须解决的问题[1]。
为了使无功功率得到最合理的配置,在配电网的关键节点进行无功功率补偿就显得尤为重要。因此,开展中低压配电网无功补偿技术的研究,对帮助降低线路损耗,改善配电网的功率因数,提高电力系统电压质量有重要意义[2]。近年来,随着科学技术的发展和人们生活质量的提高,非线性负载的使用导致电网的电压和电流发生严重畸变,含有大量谐波,进而严重影响电网质量,影响设备的正常运行,给企业的安全生产带来严重后果。因此,为了提高电网的供电质量,对无功功率和无功补偿技术研究非常有意义[3]。
1 中低压配电网的无功补偿
1.1 配电网无功补偿基本原理
区别于对外做功的有功功率,无功功率是一种在电气设备中用于建立和维护磁场的功率,由于在电网中存在着大量的变压器与电动机,根据电磁感应原理,想要在用电设备的两端建立起稳定的电压以维持其正常工作,电气设备就必须从电网中的无功电源汲取足够大小的无功功率,从而建立起正常的电磁场来维持设备的运转[4]。
假设负载的复阻抗为Z,当电流流过负载时,可得到如图 1所示的阻抗三角形。若负载的电抗值为零,即为纯电阻负载时,流过负载的电流和其两端电压具有相同的相位角,此时电网只消耗有功功率;若负载的电抗值不为零,此时的电压和电流存在一个相位差ϕ,则电网除了消耗有功功率外,还要消耗一定量的无功功率,可知,电抗值越大,相位差ϕ 就越大,消耗的无功功率就越多。

图1 负载阻抗三角形
在电力系统中,把电压电流相位差ϕ 的余弦值cosϕ 称为功率因数,由电路原理可知,功率因数同时可以表示为有功功率与视在功率的比值,电力系统中的有功功率P、无功功率Q和视在功率S存在如下关系式:

根据式(1),可以得到如图2所示的功率三角形。从图中可以看出,若无功功率Q为零,即ϕ 为零则有功功率P就是视在功率S,此时相当于输电设备提供的能量全部用于用电器的做功,电能得到最大化的利用,功率因数为1。然而实际的配电网中,由于感性负载的存在,必将导致有无功功率在系统中流动,若要使负载端消耗的有功功率不变,只能提高输出的视在功率,即输电设备的容量,这相当于增加了电力设备的投资和运行维护的资金,此时功率因数小于1。

图2 功率三角形
可见,无功补偿的实质是提高电力系统的功率因数从而提高电能的利用率。无功补偿基本原理图如图3所示。

图3 无功补偿原理示意图
用户端所消耗的功率为 P+jQ,为了补偿无功功率Q,在配电变压器低压侧配置无功补偿装置,则用电设备所需的无功功率由无功补偿装置就地提供,这就使输电线路中传输的无功功率大大减少,系统的功率因数得以提高。
1.2 无功补偿的控制策略
依据负载侧测得的无功功率指令信号,结合继电器对无功投切信号进行滞环控制,其实现原理图如图4所示。

图4 滞环控制原理图
从三相电网中捕捉三相电压电流,根据功率因数算出所需补偿的无功功率 Qc,并以此为指令信号导入继电器中。继电器根据所设定的上下限阈值与无功量进行比较,当无功大于上限时,继电器输出信号为1;当无功低于下限时,继电器输出信号0。
T1、T2、T3、T4为滞环输出信号,它们被引入触发单元中,当信号为1时,则导通对应信号的电容器组,为零则切除相应的电容器组。本文依据此法,将指令信号与投切状况例举表展现见下表。

表 滞环控制策略投切控制示意表
2 无功补偿触发系统的设计
从图5中可知,在设计触发电路时,TSC的触发角应严格按照峰值触发机制,以防止导通瞬间产生过电流,而TCR则应使其触发角保持在90°~180°之间。由于本文主要以模拟TSC和TCR的控制原理为主,旨在实现其精准的投切,而没有设计到晶闸管触发角的计算,所以当控制单元判定一组TSC进行投切时,触发单元中的锁相环模块将采样电网电压并进行同步,于电网电压自然换相点处给出触发脉冲。而当控制单元判定TCR进行投切时,需先通过一组计算电路,当投入无功量为负值时,认为系统发生了过补偿,此时计算电路将直接导出触发角90°,脉冲信号于90°点给出,TCR全导通;若是无功量为正,计算导出的触发角就为 180°,认为此时TCR关断[5-6]。
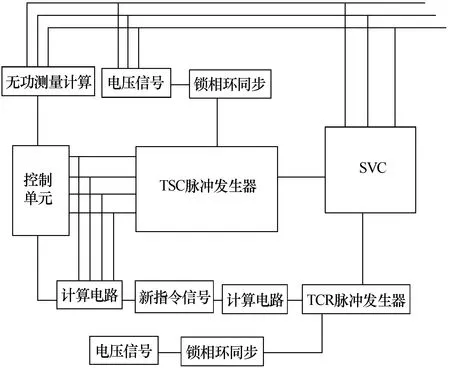
图5 触发系统电路图
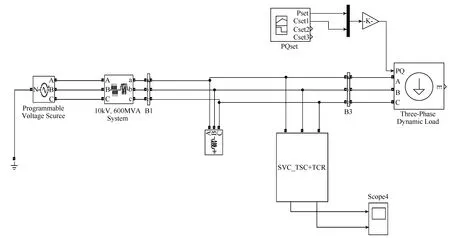
图6 无功补偿仿真模型
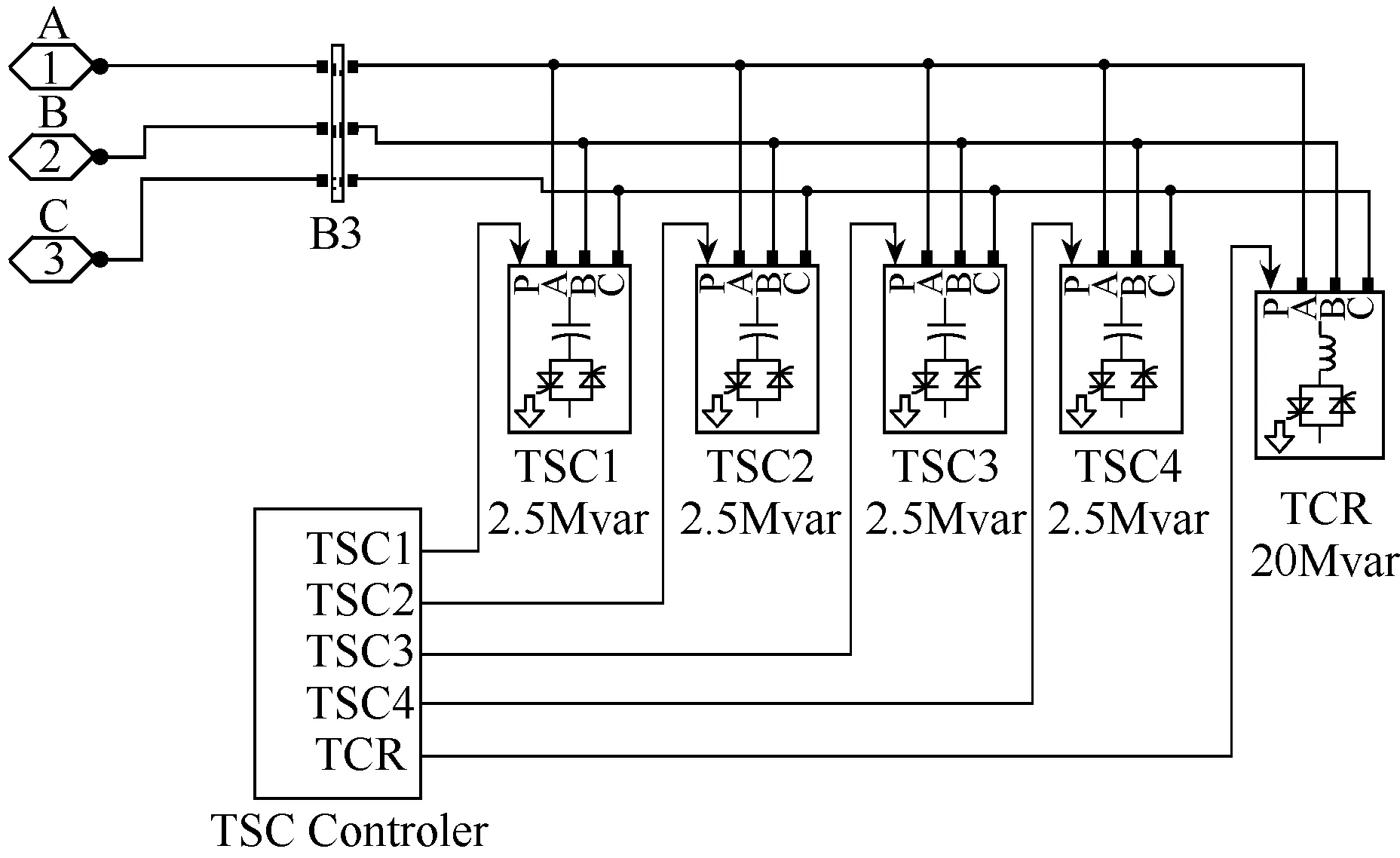
图7 SVC_TSC+TCR仿真图
2.1 无功补偿的仿真模型
用中低压配电网作为补偿对象进行研究,分析其补偿的实现过程以及出现的效果,并且搭建无功补偿模型进行验证可行性。图 6为无功补偿仿真总模型图,其中TSC、TCR以及控制模块封装于节点B3前的SVC_TSC+TCR模块内部。
图6中电源侧通过串联一个三相负载,模拟出了一个10kV、600MVA的电力系统,负载端为一个由外部信号控制其功率的三相动态负载,线路上则通过并联一个 3MW、0.2Mvar的负载来模拟输电线路的线损、杂散损耗以及电晕损耗等系统本身的特性。B1节点与B3节点内封装了三相测量元件,用以测量补偿前后电网的电压电流变化情况。其核心模块SVC_TSC+TCR的内部示意图如图7所示。
根据负载的无功值,设计的是4个TSC型补偿器和1个TCR补偿器进行配合使用,补偿容量可调,这里设置为5Mvar和20Mvar。5个补偿装置的输入端分别与控制模块相连,通过控制模块给出的触发信号来实现对补偿器的投切,补偿器由触点 1、2、3并联配置于电网中。
为了考察TSC和TCR的投切情况和补偿能力进行仿真。最后,通过仿真前后电网电流波形的大小以及电压电流相位差来分析补偿效果,并根据TSC投切信号图结合仿真前后电网侧无功量来判定TSC和TCR的投切状态。
2.2 固定感性负载的补偿仿真
由于无功补偿实质上是以补偿感性无功量为主,这里将设置一固定不变的感性负载来考核TSC的补偿能力,其模型建立如图8所示。

图8 无功负载Qset1
通过图8中无功负载模块的建立可知,把信号模块的输出 Qset1导入三相动态负载,则负载的有功功率与无功功率将按照信号模块里所设值进行变化,其仿真结果如图9所示。

图9 固定感性无功
从图9中看出,负载的有功功率固定为19.9MW,而在0.24s的时候,将产生一个幅值为14.9Mvar的感性无功功率并一直保持到2s后结束。把系统的运行时间设为2s,运行仿真后得到图10所示的电压电流波形图。
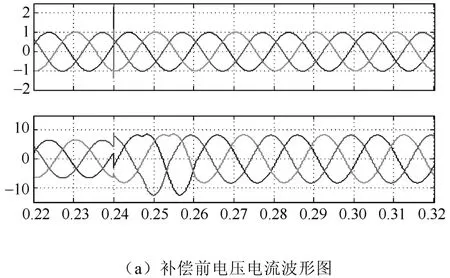

图10 中采集了0.22~0.32s内的电压电流波形。图10a中,电流波形在经过0.24s这一点时发生了畸变,此点即为无功负载的投入点。0.24s之后的电流幅值明显变大,且其滞后于电压一个相位。补偿后的波形如图10b所示,电流波形于0.24s后,经历了一个周期的时间(0.02s)基本恢复了正常幅值,与电压的相位差也显著缩小,波形在0.28s时趋于稳定。从电网侧的无功功率变化图可以更加直观地看出补偿情况。
在图11的示意图上,从0.24s开始,到0.28s,历经约两个周期的时间,无功功率基本实现了全补偿。再看TSC的投切信号图,如图12所示。

图11 无功功率变化示意图
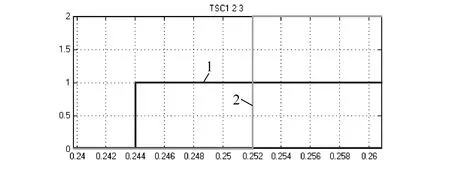
图12 TSC投切信号图
在图12中,将4组输入的TSC信号分别乘上1、2、3、4,即可在示波器中清楚地看到各组TSC的投切情况。图12中的实线1为TSC1,其在0.244s时导通,实线2为TSC2,在0.252s时导通,可见反映时间非常的短,具有很好的速动性。根据设定的阈值,当无功功率 Q>3Mvar时,导通第一组 TSC,Q>9Mvar时,导通第二组,第三组TSC的导通条件为Q>15Mvar。负载设定的无功值为 14.9Mvar,应投入两组TSC,结合图12可知,TSC实现了正确的投切。
3 结束语
本文对无功负载进行了仿真研究。即检测负载侧的无功电压电流,求得所需补偿的无功容量 Qc,把变量Qc作为指令信号,配合继电器预设的滞环宽度,给触发单元发出相应的导通信号,触发单元根据所得信号,发出相应的触发脉冲,SVC投入运行。把补偿前后的电网电压电流波形图进行对比,补偿后的电流波形恢复到了补偿前的幅值大小,并与电压具有相同的相位,实现了补偿。另外,根据补偿后的无功测量值和电容器投切信号图,得知SVC准确地进行了投切。

