基于灰箱模型快速预测中庭自然通风量的研究

曹荣光 晁江月 薛鹏

1中国建筑设计院有限公司

2北京工业大学绿色建筑环境与节能技术北京市重点实验室

随着城镇化进程推进、人民生活水平提高、第三产业比例加大，我国建筑能耗将在较长时间内保持刚性增长趋势，建筑节能被认为是我国实现2030年碳排放达峰目标的关键[1]。在过渡季节或是环境允许的条件下，利用自然通风降低建筑能耗是一种行之有效的方法[2-6]。对于我国夏热冬冷地区建筑，自然通风能够延长非供暖空调时间，延缓供暖空调设备的开启。自然通风的驱动力可分为热压、风压或其组合[7]。仅靠热压浮力驱动的通风通常是自然通风的最坏情况，特别是在温暖无风的日子。因此，在自然通风设计中，浮力驱动的热压通风效果始终是一个需要关注的问题。

为了评估和预测热压通风的流量，通常采用解析解，经验解，实验测量和计算机模拟等方法。解析模型是从质量和能量的守恒方程来描述简单的通风问题，比如单向流动[8]。Linden等人得到了一个单层建筑的两级开口气流速度的分析表达式[9]。Fitzgerald和Woods建立了一个分析模型来揭示两个开口的热压通风效果[10]。经验模型通常应用在设计手册或指南中，其公式中的系数保证该模型在一定范围内准确[11]。Hayden等人根据67个独立房间的数据开发了一个经验模型来描述流速[12]。实验模型已被广泛用于预测建筑物的通风性能。Kotani等人通过缩小尺度的实验方法研究采光井中由热压驱动的自然通风量[13]。一般来说，实验更准确可靠，但是花费大量时间和金钱。因此，在大量的文章中，实验主要是为了验证数值模型，特别是CFD模型。在过去的研究中，CFD仿真已经被证实可以预测具有单个开口[14]或两个开口[15]的建筑物中的气流组织和通风量。目前CFD仿真针对复杂建筑（如中庭建筑）仍然需要大量的计算时间，有必要找到一种替代方法来快速预测具有多个开口的中庭热压自然通风量。

在以往的研究中，通过上述方法对通风量进行了预测，其影响因素也被广泛研究。这些因素包括室外温度[16]、热源的特性[17]、开口面积[18]、立面设计[19]和窗户结构[20]等等。这些发现表示一系列合理的参数可以保证中庭良好的热压自然通风效果。然而，研究同时发现，随着通风量的不断优化，中庭的通风能力存在瓶颈。

本研究在以上研究的基础上，以某建筑中庭为例，提出了一个基于灰箱模型的新方法，来预测三个开口中庭的热压自然通风量。首先模拟该中庭在不同边界条件下的通风量，进而通过理论分析，建立热压通风量预测的灰箱模型。基于模型结构对模拟数据进行回归，得到中庭通风量的半经验公式，并对其进行验证。此方法为类似中庭的前期辅助设计提供了一种简单科学的研究思路和计算方法。在准确的前提下减少大量的脑力劳动和时间，同时可以帮助设计师估算通风性能并选择最佳的中庭开口设计。

1 数值方法

1.1 物理模型

该中庭底部两层分别为与室外相连的门和窗，顶部为可开启的玻璃窗结构。一层门可开启面积为774 m2；二层窗户最大可开启面积为2385 m2；中庭顶口面积为838 m2；地板热源面积为4860 m2。依据建筑总平面图并按照不影响室内风场为原则进行几何模型简化，利用软件Gambit软件建立中庭物理模型，如图1。

本研究关注建筑中庭热压通风的对流传热现象。首先对计算区域内的空气流动进行如下假设：

1）中庭热压通风气流速度在5 m/s以下，对气流的密度影响很小，因此空气当作不可压缩流体对待；

2）满足Boussinesq假设。在计算动量方程中与体积力有关的项时考虑密度的可变性，其它方程求解时密度作为常数；

3）由于室内人员众多，人员散热较大，所以将人员负荷折算成热流密度，近似设置为地面散热，灯光负荷设置为壁面和顶面散热。

图1 中庭及相连建筑示意图

1.2 数学模型

采用FLUENT软件计算中庭的速度场和压力场，并采用连续性方程、雷诺时均-纳维叶斯托克斯和标准k-ε湍流方程进行求解。其相应的运输方程为：

式中：Ф是通项，可以代表分速度 u、湍动能系数k、湍动能耗散率ε；ρ是气体密度，kg/m3；Г是广义扩散系数；SФ是Ф的源项。

计算域为整个中庭建筑，该模型的网格由大约448万个非结构化单元组成，建筑开口周围的区域进行加密网格处理，该网格数是在对其数量进行独立性灵敏度分析之后确定的。开口的初始边界条件设定为无压力差的压力入口（Pressure Inlet）或出口（Pressure Outlet）。室外温度选取典型气象年数据设定。在k-ε湍流模型中，其经验湍流系数分别为C1=1.44，C2=1.92，Cμ=0.09，σε=1.3 和 σk=1.0。采用 PISO 假设计算压力与速度耦合，采用二阶迎风格式对密度，动量和湍动能项进行离散化处理。

在中庭中，热量的源项主要包括人员的发热量和其他设备的发热量。根据建筑设计提供的方案资料，人员密度约为6 m2/人，照明及设备功率约为25-30 W/m2。根据文献[21]选择房间类型为商场，劳动强度为轻度劳动，群集系数为0.89。室内温度在24℃下，成年男子显热69 W，潜热112 W。可以得出，人群热流密度约为26.85 W/m2。走廊墙面与顶面的热流密度为10.36 W/m2。

2 影响中庭通风量的因素分析

对自然通风的优化，首先要以通风量为因变量。27个案例被用来分析其潜在因素对通风量的定量影响。底层开口大小（A1）、中间层开口大小（A2）、顶层开口大小（A3）、热源强度（E）以及室外温度（To）等 5个自变量在不同方案中设计成了不同值，h（底层和顶的距离）和h'（二层和顶的距离）分别根据实际情况分别设置为19.6 m和14.4 m，各案例通风量结果如表1所示。

表1 案例设置及中庭排风量结果汇总

2.1 中庭顶部开口面积的影响

从表1可以看出，6个案例（1-1至1-6）被设计用来检验中庭顶部开口面积对排风量的影响。所有案例一层设置100%开门，二层无开窗，室内发热为252 kJ/s，室外气温14℃。随着开启率从10%增加到70%，空气的流量从164 m3/s增加到282 m3/s，但随着开放的增加，增长率逐渐下降。为了研究这种现象，在图2中测试并提供了具体气流组织的矢量图。

图2 中庭顶部开口处的双向流动速度矢量

在开启面积50%以上后，通风量增加趋势趋于平缓，这是因为开口面积的增大使开口压力下降，致使一定量的冷空气冲中庭顶部进入中庭，出现回流现象如图2。

2.2 一层外墙开门面积的影响

5个案例（3-1至3-5）被设计用来研究门的开口面积对中庭排风量的影响。所有案例二楼开窗率设为20%，顶部开度为30%，总室内热通量为252 kJ/s，室外空气温度为14℃。随着开门率从20%增加到100%，空气出流量从140 m3/s增加到271 m3/s。这表明，一层门的开启面积是影响通风量的关键因素。

2.3 二层外墙开窗面积的影响

6个案例（2-1至2-6）被设计用来研究二层窗户开口面积对中庭排风量的影响。一层门的开启率设置为100%，顶部开度为30%，室内总热通量252 kJ/s，室外气温14℃。二层窗户开启程度为10%时，中庭排风量突增29 m3/s。但是，随着窗户开启率从10%变化到50%，流量变化不大。这可以表明，开窗后通风能力迅速达到平衡状态，随着开窗面积的进一步增大，中庭内的空气流量没有明显变化。

2.4 室内热功率的影响

根据文献[22]，计算了四种不同活动状态下的人体产热量。4个案例（4-1至4-4）中，一层门开启率为100%，二层开窗率为20%，顶部开口率为30%，室外气温为14℃。随着室内热功率从291 kW减少到199 kW，中庭排风量从293 m3/s下降到251 m3/s。热源热量越大对中庭的自然通风作用越强，两者关系几乎是线性的，这说明了中庭的热源是影响通风效果的关键因素。

2.5 室外温度的影响

9个案例（5-1至5-9）被设计用来研究室外空气温度对中庭排风量的影响。所有案例均设置一层门开启率100%，二楼开窗率30%，顶部开口率50%，总热量252 kJ/s。当室外空气温度从10℃上升到26℃，室内外压力差减小，空气出流量从327 m3/s降低到310 m3/s。结果表明，虽然浮力驱动的热压自然通风受外界气温的显著影响，但是通过一定的门窗开度设计和室内热源控制，中庭的自然通风量可以保持在较高的水平。

3 灰箱模型辨识

为了对中庭热压通风量进行预测，需要建立半经验公式。虽然中庭结构皆不相同，但基本影响因素相同。本研究从理论上对热压通风形式进行详细的自变量因素识别，建立基本模型结构并确定自变量与目标函数的简单关系。最后通过代入模拟数据对灰箱模型进行系数回归，并对得到的半经验方程进行预测验证。一般而言，对特定模型的辨识是一个递推过程[13]，如图3：

图3 灰箱辨识示意图

3.1 参数估计与灰箱模型结构的建立

在进行基本通风量求解时，采用安德森完全混合假设，该假设认为室内温度为统一均匀值，因此空气密度也定值。在进行双口通风计算时，采用布鲁斯中和面假设，即存在一个高度的余压为0，两个开口距离中和面的高度分别为h1和h2。其物理模型参数关系如图4所示：

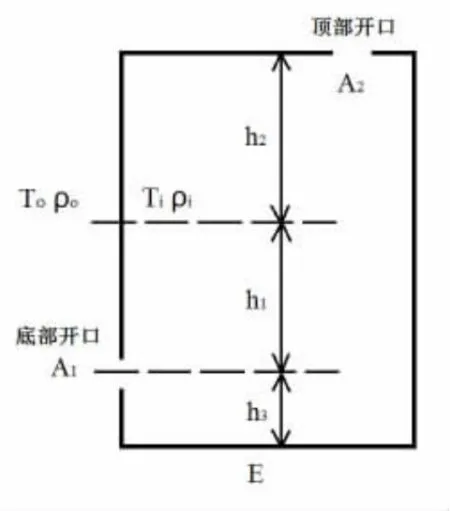
图4 双开口模型中的自变量

图中A为地面面积（m2）；ξ为风口局部阻力系数；h为距离（m）；ρ为空气密度（kg/m3）；T为室内空气温度（K）；E为地板热流密度（W/m2）。

两个开口的余压分别为：

通过伯努利方程可以得到：

出口和入口的空气质量流量分别为：

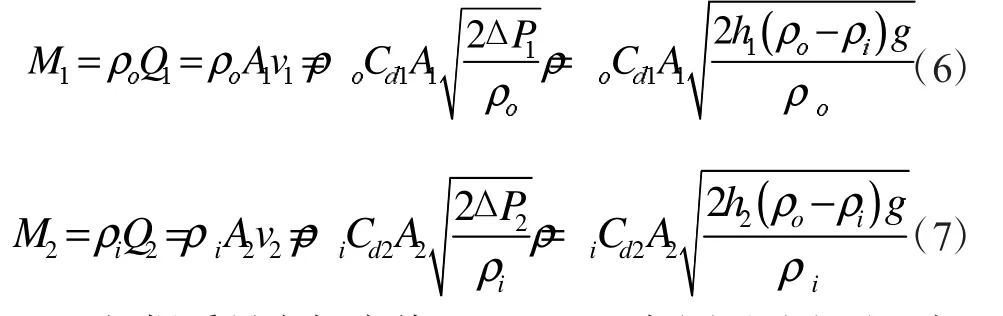
根据质量守恒定律 M=M1=M2，式（6）和（7）可以变化为：

在自然通风中，空气可假设为不可压缩流体，则：

将式（9）代入式（7），得：

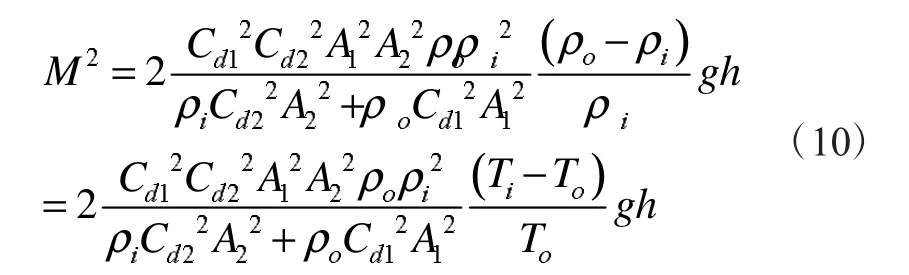
根据能量守恒定律：

其中cp是空气的等压比热容，将式(10)代入式(9)，得：

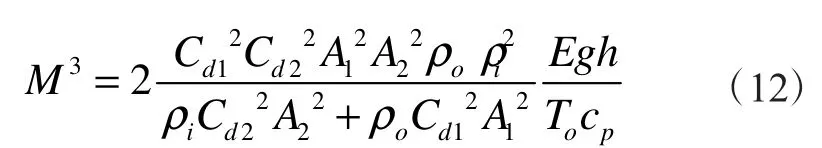
将式(6)代入式(11)，得中庭排风量为：

对于两个进口一个出口的中庭来说，可以假设顶部开口一部分排的是第一个进口的风，排风面积为βA3（0<β<1），另一部分排的是第二个进口的风，排风面积为(1-β)A3。这样就可以直接套用式（14），得出三开口中庭排风量的表达式为：

式中：h是第一个进口和顶部开口的高度差；h'是第二个进口和顶部开口的高差。是待定参数。

3.2 灰箱模型的系数求解

对于已经建立的灰箱模型，还需要通过模拟数据对其系数进行回归求解，以确保模型的准确性和适用性。本研究以穷举法和最小二乘法的结合为优化原则，采用编程的方法对灰箱模型进行系数回归。求解数据为以上模拟的27组结果。编程采用Matlab，过程中有5层循环进行相互嵌套，得到结果精确到小数点后三位。通过整个灰箱模型的辨识，我们便得到了适合于此建筑热压通风通风量计算的灰箱半经验公式：

每种情况下的预测值可以通过这个方程计算出来，CFD模拟和半经验预测之间的空气流量比较如表2所示。在案例1-1中，由于顶部开口较小，阻力较大，增加了气流运动的复杂程度，因此最大误差为8.89%。在另外26个案例中，误差均小于5%，这表明此半经验公式的曲线拟合较好。

表2 案例的模拟通风量和半经验公式计算通风量比较

3.3 灰箱模型的验证

为了验证该灰箱模型的正确性和准确性，本研究将针对5个影响因素，采用6个新边界条件进行模拟验证，新案例的设置如表3，结果如图5。

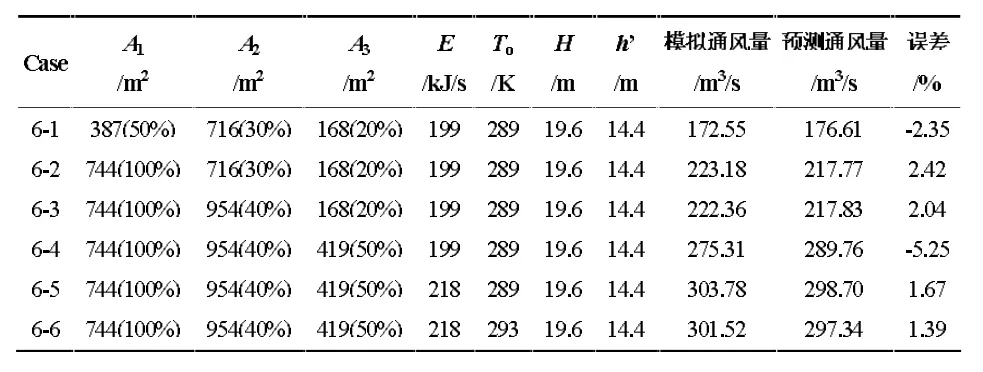
表3 新案例的设置

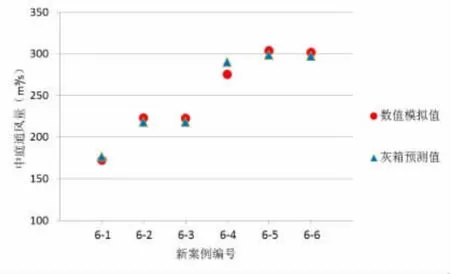
图5 新案例通风量的模拟值及预测值比较

从图5可以看出，所有案例的预测误差均小于6%，这表明半经验预测与CFD模拟结果一致。可以得出此基于模拟的灰箱预测模型可以在新案例的计算中代替CFD模拟对中庭热压通风量进行预测计算。

4 结语

本研究以建筑中庭为研究对象，建立了物理模型和数学模型，通过CFD对其自然通风效果进行模拟，定量分析了室内负荷、进出口面积和室外温度等因素对热压自然通风量的影响，结果表明，通风量与进出口面积和室内热功率呈正相关，同室外温度呈负相关。

基于灰箱模型方法，提出了一个快速预测通风量的半经验方程。利用新案例数据对该方程进行验证，结果表明，此预测方程对模拟数据的预测误差在6%以内。此方法为建筑中庭设计中自然通风量的计算提供了一种简单科学的研究思路和快捷的计算方法，可以快速估算通风性能以便选择最佳的中庭开口设计。

本研究提出的灰箱模型是基于模拟数据针对某一建筑进行预测的。不同的中庭建筑有相同的基本模型，但根据其特殊结构存在独有的半经验公式。下一步作者将根据该模型对实验数据进行回归求解，并验证得到的半经验公式。同时为了提高精确性，将进一步考虑室内温度和密度的不均匀性。