逐步回归和神经网络对睡眠质量影响因素分析①

，

(安徽财经大学金融学院, 安徽 蚌埠 233000)

0 引 言

睡眠质量问题危害着许多现代人的身体健康和心理健康，因此对睡眠质量问题的研究分析也引起了国内外学者的广泛关注。目前对睡眠质量影响因素的研究主要是以单个指标为主，如索艳凤对年龄影响睡眠质量的研究等。单个因素研究只能提出改善方案，却无法建立预测模型作为诊断依据。开展对睡眠质量的研究分析和探索睡眠质量影响因素，研究各因子对睡眠质量的影响大小，构建预测模型，为制定科学的干预策略和治疗方案提供了理论和研究依据。

1 数据来源及模型假设

数据来源自第七届亚太地区大学生数学建模竞赛A题。为了方便构建模型，特提出以下假设：(假设数据来真实、可靠和准确，既数据为实际人们的睡眠状况的反映；(为了使模型简单有效，对部分异常值进行了剔除，假设这样的数据处理对结果产生较小的影响；(选取的睡眠质量影响指标具有代表性，不考虑未选取的指标对实际情况的影响。

数据预处理：利用箱线图对异常值进行剔除，以及个别极端值，因为这些诊断结果可能受到其它因素的影响。

2 基于逐步回归对睡眠质量影响因素的分析

2.1 研究思路

首先对根据实际情况对数据进行标准化等措施进行了预处理；其次使用Excel软件对各睡眠指标进行了取整处理，并利用箱线图分析其间线性关系；最后，运用SPSS软件进行逐步回归，得到最优回归方程。

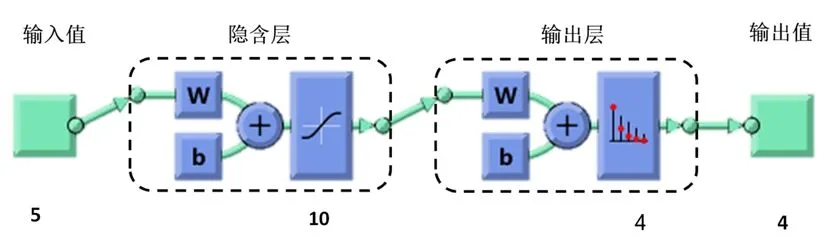
图1 神经网络模型结构图

2.2 预处理

附件数据存在一定的异常值会对构建模型产生一定的影响，为了使结果准确，使用箱线图删除了73个极端异常值。此外，为了避免数据量纲对回归产生影响，将样本中六个睡眠影响指标数据进行归一化处理。

(1)

式子中：xi为归一化后的变量，yi为归一化后的变量，minx为该项自变量中的最小值，maxx为该项自变量中的最大值。

2.3 实证分析

以附件Ⅰ中给出的六个睡眠影响指标Age, Character, Nervousness, Psychoticism, Reliability, Sex为自变量，将睡眠质量作为因变量。进行多元逐步回归，入选变量标准为0.05，剔除变量标准为0.01.利用SPSS软件进行逐步回归分析，得到如表1所示。

表1 睡眠质量影响指标逐步回归多元线性回归结果

由上表可知，对睡眠质量有显著影响的变量有年龄x1、焦虑度x3和性别x4，而性格x2、神经质x4和可靠性x5在回归过程中被剔除；逐步回归的拟合结果为0.63，拟合优度表现不是很好；不过回归方程的显著性较高(F=87.364，对应概率值p=0.000<α=0.05)；各变量的回归系数都比较显著(各变量的t统计量概率值p<=0.05)；并且各变量之间的多重共线性较弱(VIFi的值均接近于1)，因此不存在因为自变量之间相关性较显著被剔除的情况。由逐步回归得到最终方程：

yi=0.686x1+0.614x3-0.092x3+1.575

2.4 结果分析

从回归结果可以看出，睡眠质量主要与年龄、焦躁度和性别有关，而性格，神经质，可靠性和睡眠质量则不相关。睡眠质量与年龄和焦躁度呈正相关，和性别呈负相关，既年龄和焦躁度越大，睡眠质量越差，女性的睡眠质量普遍比男性要差；而睡眠质量受性格、神经质和可靠性的影响较小。

3 基于BP神经网络对睡眠质量影响因素的分析

3.1 研究思路

利用神经网络函数进行模式识别，五项睡眠影响因素作为输入量，睡眠质量作为输出量，然后选取大量数据进行神经网络的训练，选取少量数据对得到的神经网络模式识别模型进行检验和测试。然后对神经网络进行反复训练和改变隐含层数目，使得交叉熵(Cross-Entropy)和误判率(Percent Error)达到理想的最低值，最后预测检验模型是否有效。

3.2 研究方法

BP神经网络主要就是由工作信号正向传递子过程和误差信号反向传递子过程这两个过程组成。单个样本有m个输入，有n个输出，且在输入层和输出层之间通常还有若干个隐含层。

由于诊断结果繁多，所以应该先对不能进行分类的诊断结果进行数据剔除，然后保留主要的诊断结果，为保证数据统计口径和方法的一致性，仅选取了数据来源是门诊的样本，另利用箱线图剔除各组数据中的异常值，将问题简化为5维4分类的模式识别问题。然后采用利用BP神经网络模型对数据进行模式识别，然后对神经网络进行反复训练，使得交叉熵和误判率达到理想的最低值，得到最优的神经网络模型。

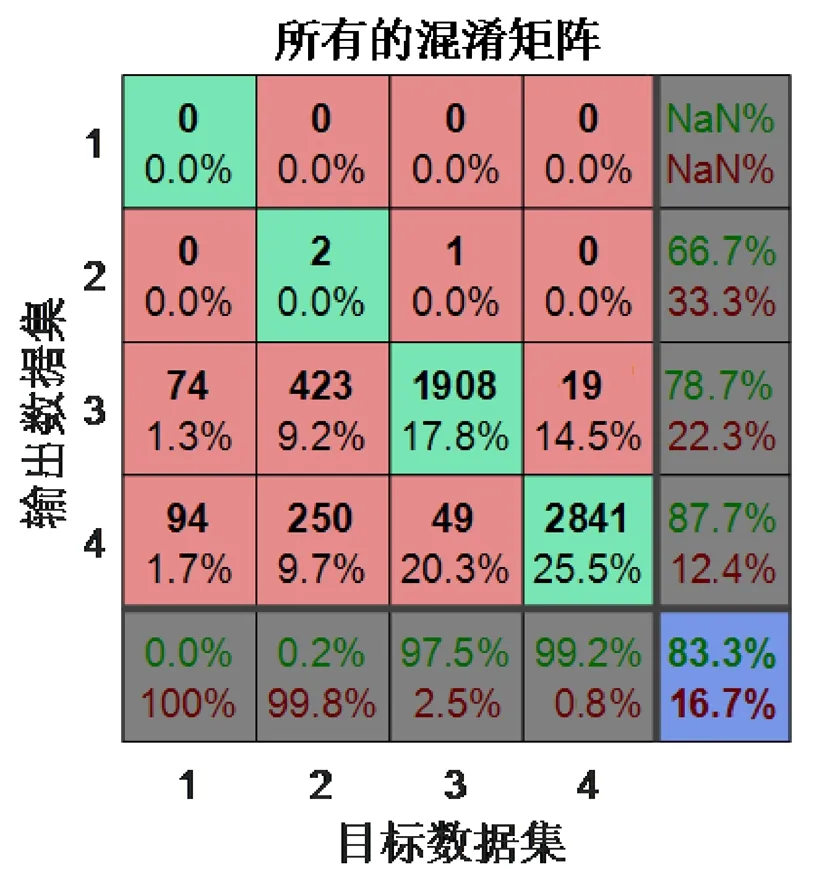
图2 总样本的混淆矩阵

3.3 实证分析

附件二有六种睡眠影响因素影响睡眠质量。将睡眠质量影响因素作为输入量，睡眠质量作为输出量，构成了6个输入4个输出的网络。选取附件二中90%的实际数据作为训练样本集，5%的数据进行预测检验样本，5%的数据作为测试样本集。

选取的BP神经网络模型是由一个输入层、五个隐含层和一个输出层组成，由图1所示。

对于给定的输入，仅有小部分靠近的中心被激活。然后可以利用MATLAB中的神经网络工具箱实现我们的人工神经网络的功能，由于影响诊断结果的各项睡眠质量影响因素自变量有5个，睡眠质量作为因变量被分为4个等级。所以输入神经元的个数取为5，输出神经元的个数取为4，取90%的样本数据进行神经网络训练，5%用于检验，5%用于测试。 隐含层在调试过后得到交叉熵和误判率最小时应该取10个隐含层。最后在隐含层确定为10层和训练、检验、测试比率分别为90%、5%和5%时。经过多次再训练后得到最低的交叉熵和误判率的神经网络模型。

最后在反复训练过后得到一组Cross-Entropy和Percent Error较低的神经网络如表2所示：

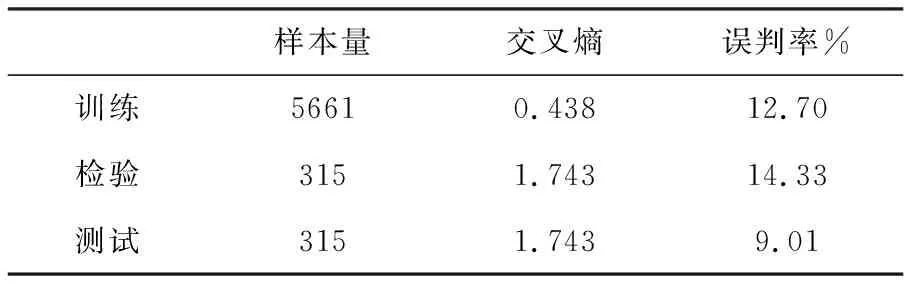
表2 各个样本量训练效果表

最后的训练样本的误判率控制在12.70%。

图2显示了三种数据组合的混淆矩阵。网络输出是非常准确的，正如我们可以看到在正确的绿色方格所显示正确反应以及错误的红色方格所显示的错误判断反应。右下蓝色正方形显示了整体精度。如图2所示

其中绿色的方框显示其对正确数据的影响率最高达97.5%, 而红色的方框显示了其对数据错误的影响率低至16.7%，最后一个混淆矩阵的蓝色方框显示了最后的整体的精度高达83.3%。所以经过分析后，该神经网络模型已被训练到理想状态，其所得到的函数模型可以被用于患者精神疾病的诊断。

得到在不同的绘图区间取值下对应的交叉熵取值，如图3所示：

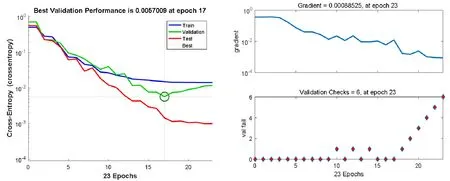
图3 网络训练过程梯度等参数变化

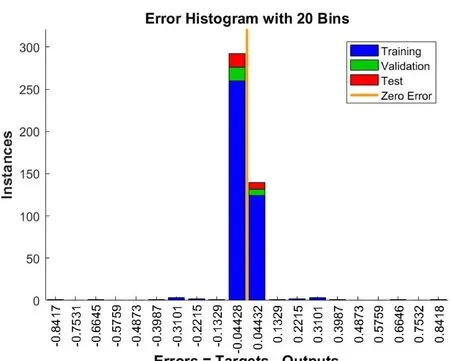
图4 20仓误差直方图

因为交叉熵越低越好，所以从图中可以得出当绘图间隔取为23 Epochs时交叉熵最低。点击神经网络模式识别工具中的训练状得到训练状态记录图。从图3可以得到不同绘图间隔下的训练状态值，可以得到梯度和VAL失败分别23Epochs时得到最高值6。

最后在每次训练后对各项指标进行分析后得到最优理想值和神经网络模型，最后通过MATLAB将训练出来的神经网络保存为一个神经网络模型，可作为后续研究预测的工具。

4 对比分析

为了对比二者回归预测的效果，随机抽选了100个样本数据，分别利用逐步回归函数和神经网络模式识别函数进行回归预测，对比二者的预测效果。利用箱线图将实际目标值和两种模型的预测值的散点图画出来，如图5所示。

图5 回归预测效果散点图

由图像能够明显看出逐步回归预测偏离实际值的点更多，神经网络的预测效果更好。而从实际的结果也是这100个样本量中，逐步回归模型仅达到了63%的准确率，而神经网络模式识别模型达到了89%的准确率。这也得出了神经网络模型在回归预测上面占有绝对的优势，但是却不能剔除无关或是影响因素极小以及重复的因变量。正如逐步回归模型得出睡眠质量和性格、神经质、可靠性这三个因素相关性较小，所以不纳入回归方程，神经网络模式识别模型却不能做到这一点。

在睡眠质量影响因素的分析上，逐步回归模型的应用空间非常大，但是回归效果却较差，原因可能是因为各自变量和因变量不是简单的多元一次模型，也可能是多元多次模型，后继研究可以在此基础上进行改进。而神经网络模式识别却在回归预测上占用绝对优势，误判率远远低于逐步回归模型。但是二者的误判率均高于10%，证明模型还有进一步地改进空间，也可能是自变量较少，影响因素未被完全发掘等原因。

5 结 论

从逐步回归的结果可以看出睡眠质量与年龄和焦躁度呈正相关，和性别呈负相关，既年龄和焦躁度越大，睡眠质量越差，女性的睡眠质量比男性要差；而睡眠质量受性格、神经质和可靠性的影响较小。

因此对医疗工作者以及相关研究人员提出以下建议：

a. 针对不同年龄，性别的人群采取不同的治疗方案。如在逐步回归结果得知年龄对睡眠质量影响最大，随着年龄的增加睡眠质量逐渐降低，性别也会影响睡眠质量。年龄较大的人或是女性的睡眠质量较差，可以针对这部分人采取专门的治疗或是诊断方案。

b. 焦躁度过高不利于睡眠，需要研究降低焦躁度的方法。逐步回归结果显示焦躁度会很大程度影响睡眠质量，研究降噪焦躁都的方法能从根源上解决睡眠质量的问题。

c. 进行进一步收集数据与临床试验，得出导致不同年龄与不同性别人群睡眠质量存在差异的内在原因。通过更多的数据和临床试验，完善影响睡眠质量的指标体系，提高神经网络识别模型的预测精度，后继可以进一步改进的神经网络模式识别模型应用临床诊断中去。