基于zigbee和量子遗传算法的无线传感器网络节点定位技术研究①

， ， ，

(长安大学汽车学院，陕西 西安 710064)

0 引 言

随着传感器技术、现代网络及无线通信技术的迅速发展，大规模分布式传感器网络(Wireless Sensor Network, WSN)在生物医疗、环境监测、军事国防等领域应用越来越广泛，WSN已成为当今世界最热门的研究领域之一[1][2]。国内外许多学者对WAN节点定位做了大量研究，如Benha University的Mohamed等人提出将整个网络划分为多个子区域并分别进行未知节点定位的改进的DV-Hop定位方法[3][4]；南京邮电大学的王萍萍提出的一种将TDOA算法和RSSI算法组合的定位方法，其根据锚节点离未知节点的距离长短选择不同的算法[5][6]；武汉理工大学的王晓丽提出的基于模拟退火算法对DV-Hop算法的平均跳距进行修正的定位方法[7]。这些定位方法与传统的节点定位方法相比精度得到提高，但对更高精度的应用场合则不能满足要求，同时定位响应速度也有待提高。

提出一种基于量子遗传算法的无线传感器网络定位技术，通过分析未知节点周边锚节点的数量，将定位情况进行分类，依据未知节点与锚节点的测量距离，建立定位优化模型，最后用量子遗传算法对模型求解。仿真结果表明，量子遗传算法比传统遗传算法有更出色的收敛性，在节点定位精度方面也比传统DV-Hop算法更高，可以应用于多数高精度、高实时性定位场合。

1 定位模型与算法分析

1.1 节点初始位置获取

首先，网络中的锚节点向它的邻近节点广播自己的位置信息，接收节点接收来自锚节点跳数信息同时忽略来自同一锚节点的大跳数数据，未知节点获取邻近锚节点的位置并测得与邻近锚节点的距离。根据未知节点周围锚节点数量可分为以下几种情况获取初始位置[8]：

未知节点周围锚节点个数大于等于三，可以通过三边测量法或三角测量法计算未知节点坐标。如下图1所示：

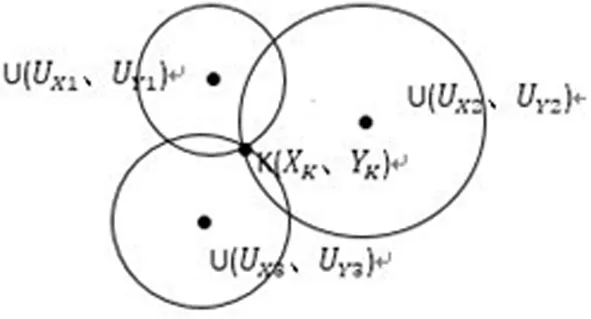
图1 三边测量法计算未知节点坐标

已知三个锚节点U1、U2、U3的坐标(UX1、UY1)、(UX2、UY2)、(UX3、UY3)及到未知节点K(XK、YK)的距离d1、d2、d3，K坐标可由式1-1计算得到。

(1)

1) 如果未知节点(XK、YK)在一跳内有两个邻居锚节点，则分别以锚节点U(UX1、UY1)、U(UX2、UY2)为圆心，以网络节点通信半径R为圆半径作圆，并在如图2所示阴影区域内采样，采样点满足下式(1-2)时保存作为未知节点初始位置，采样点门限为N。

图2 一跳内有两个锚节点

(2)

其中，DX,Ui为未知节点与锚节点U测量距离，δ为最大误差。

2) 如果未知节点(XK、YK)在一跳内仅有一个邻居锚节点，则分别以该锚节点U(UX1、UY1)和一个距离该未知节点N跳的锚节点为圆心，以网络节点通信半径R和N×R为半径作圆，并在如图3所示的阴影区域对节点初始位置采样，采样点满足下式(1-3)时，保存采样点。

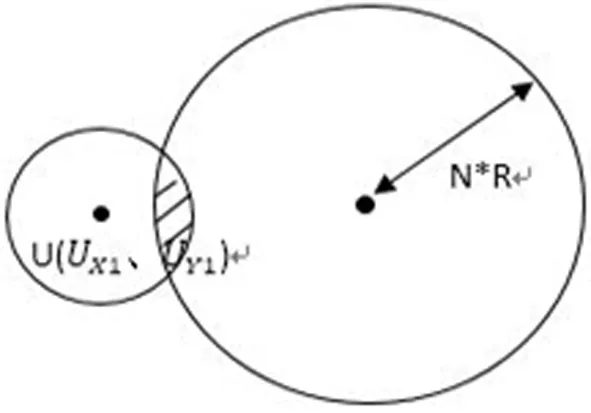
图3 一跳内仅有一个锚节点

(3)

3) 如果未知节点周围没有邻居锚节点，则以距离未知节点最小距离的锚节点为圆心，以相应的通信半径倍数为半径作圆，并在上述图相应阴影位置对未知节点采样。若经过采样后采样点分别为A1(X1、Y1)、A2(X2、Y2)…AN(XN、YN)，则未知节点的估计初始位置如式(4)所示：

(4)

1.2 量子遗传算法优化设计

算法优化过程中，未知节点根据周围锚节点数量、位置及测量距离，利用量子遗传算法对初始位置进行迭代优化[9]。

步骤一：在传感器网络内随机产生M+N个节点的网络拓扑图，其中M为锚节点个数，N为未知节点个数。

步骤二：根据上述节点约束条件，对所有满足约束条件的采样点采用量子比特的概率幅进行编码，以产生N条量子染色体， 由它们组成初始种群。

在量子遗传算法中，可用量子比特编码方式对染色体进行编码。一个量子比特有两个基本状态|0和|1，还可以对两种基本形态进行线性组合成叠加态，如式(5)所示：

|ε=α|0+β|1

(5)

其中，|α|2+|β|2=1，α、β是一对复数，成为量子态的概率幅。

用一个量子比特表示基因的两种状态，两个量子比特表示基因的四种状态，那么K个量子比特可表示基因的2k个状态，则K个量子比特的概率可用式(6)表示：

(6)

步骤三：计算上述每个采样点的适应度值并记录最优个体，适应度函数如式(7)所示，并保存最佳个体和相应的适应度值。

(7)

步骤四：对所有的采样点，参照步骤三记录的适应度值，按照轮盘赌选择法对父代进行选择产生新一代个体。高适应度的个体被选择的概率高，低适应度个体被选择的概率低。其个体i被选择的概率为：

(8)

步骤五：通过量子旋转门对量子染色体进行变异操作，以更新量子位的概率幅，从而达到基因变异、产生新一代个体的效果。量子旋转门如式(9)所示：

(9)

其中，θi为量子旋转角，可以调整其大小和方向，(α′,β′)T为更新后个体。

步骤六：记录量子旋转门变异后的个体数据，保存最佳个体，并比较目标值，若目标值小于最佳个体，则将最优解作为下一次迭代值，进行不断循环迭代。

步骤七：若经过迭代的最优解满足目标值的中止条件，则输出最优解并退出。

2 仿真分析

基于Matlab平台，在10m×10m的矩形区域内随机分布35个传感器节点，设置锚节点比例为40%，形成无线传感器网络。采用遗传算法对未知节点位置进行优化时，设置最大迭代次数为100，交叉概率PC为0.6，变异概率Pm为0.1，每次采样100个有效样本进行仿真。

图4为经过量子遗传算法优化后未知节点在无线传感器网络中的分布。其中蓝色为初始节点分布，红色为优化后的未知节点位置。

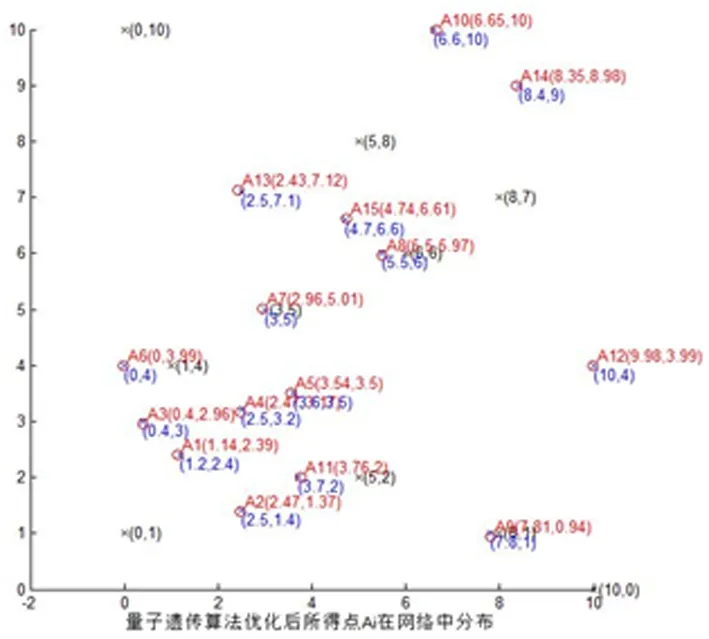
图4 算法优化后未知节点分布示意图

由图4可以看出，使用量子遗传算法对无线传感器网络定位，对绝大多数未知节点的定位十分精确，但也有少量几个未知节点的定位出现很大的偏差，其原因可能是这几个未知节点处于整个网络的边缘地带，其周围没有锚节点可供量子遗传算法进行抽样、参考优化，如两个处于网络边界的未知节点(0、10)和(0、1)。

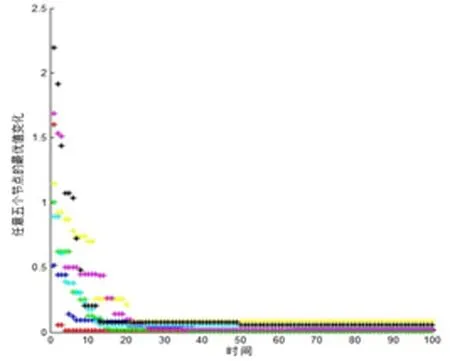
图5 任意五个未知节点最优值变化

图6 经典DV-Hop算法每个节点误差

图7 经典DV-Hop算法每个节点均方差

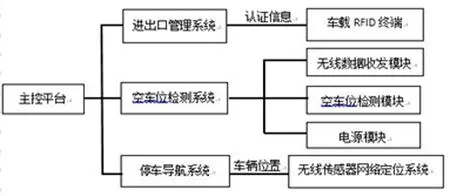
图8 智能停车场总体架构

如图5所示为抽取无线传感器网络中任意五个未知节点的最优值变化过程。可以看出，五个随机节点中红色节点在时刻5就完成了迭代优化，之后，该未知节点位置定位未出现波动；同时随机节点中最晚完成迭代的黄色节点也只到20时刻。可以看出，量子遗传算法有较高的优化收敛速度，在实时性要求较高的场合可以得到应用。

如图6和图7所示为采用经典的DV-Hop算法进行节点定位时每个节点的定位误差和均方差。可以看出参与定位的未知节点中有靠近三分之一的节点定位误差超过15%，甚至有两个节点的误差超过了20%，且对于不同的节点，其定位精度差异较大，定位精度波动明显，对于重要的定位应用场合，显然该算法不能满足精度、稳定性的要求。

3 量子遗传定位算法在小区停车场的应用

随着社会经济水平的不断发展提高，私家车数量越来越多，传统的地下停车场仅仅对车辆安全性进行考虑，已经越来越不能满足用户需求。本文通过对停车场运行效率和安全性进行考虑，设计一套基于zigbee的智能停车场管理系统[10]。智能停车场管理系统总体架构如图8所示：

4 结 语

通过查阅相关资料了解无线传感器网络在各种应用场合的需求，对比、分析了现有无线传感器网络节点定位方法的不足，提出了一套基于量子遗传算法的无线传感器网络定位算法。算法根据未知节点周围锚节点数量，将定位情况进行分类，建立节点定位优化模型，然后通过量子比特编码方式对染色体编码，对上述优化模型的采样区域进行采样，并使用传统轮盘赌选择法选择采样的初代群体，最后通过量子旋转门对染色体进行变异、不断迭代，直到达到设定的目标值。仿真结果表明：基于量子遗传算法的无线传感器网络定位算法能非常精确的完成定位，同时定位的稳定性和实时性也优于传统的DV-Hop算法，可以运用在各种应用场合。