基于改进混合遗传算法的无人车路径规划①

，

(安徽工业大学机械工程学院，安徽 马鞍山 243000)

0 引 言

无人车的路径规划技术是智能导航系统的关键环节，实现无人车路径规划的关键技术是路径规划算法，它直接决定着搜索结果的优良和搜索时间的长短，选择一个合理的路径规划算法显得尤其重要。经过半个多世纪的探索，国内外学者主要从路径规划算法的实时性、全局收敛性和运算效率这三个方面进行研究改进，已经实现了从最初的盲目搜索到智能搜索算法的发展。用于全局路径规划的算法主要有A*算法[1]、人工势场法[2]、人工神经网络算法[3]、细菌觅食算法、遗传算法[4]等，其中A*算法和人工势场算法属于传统规划算法，人工神经网络算法、细菌觅食算法、遗传算法属于智能路径规划方法。当无人车在整洁的工厂、仓库、街道等环境中工作时，空间中障碍物个数少且体积大，针对这种较简单的静态工作环境，采用自由空间法构建环境模型，根据自由空间法构建的环境模型特点，提出一种结合Bellman-Ford算法与精英交叉机制遗传算法的混合遗传算法，用于规划较简单环境中的无人车全局最短路径。

1 基于自由空间法构建无人车环境模型

采用矢量对象描述方式来描述障碍物并进行建模，将环境空间障碍物抽象表示为各种不规则多边形，环境空间W的边界为200×200，其中初始点S坐标为(10,190)，如图1中圆点所示，目标点坐标T为(190,10)，如图1中方块点所示，基于链接图法[5]使用自由链接线将环境空间划分成各种凸多边形，并基于MATLAB软件通过抽象表达环境空间和构造空间连通图两个步骤完成无人车的自由空间法建模，环境模型如图1所示。

图1 自由空间法构建的环境模型

2 基于自由空间法的改进混合遗传算法

提出一种融合Bellman-Ford算法与遗传算法的混合遗传算法，用于实现无人车的全局路径规划。这种算法的规划思路是：

(1)先用Bellman-Ford算法搜索出连通图中初始点到目标点的最短路径，获取粗路径点；

(2)然后用遗传算法优化每个粗路径点，获得无人车安全行走的最短路径。

(3)将Bellman-Ford算法与精英交叉机制遗传算法相结合构成一种改进的混合遗传算法。

这种改进的混合遗传算法使用固定长度的染色体，极大简化个体编码方法，绝不产生无效初始路径，且有效提高遗传算法的收敛速度，能够避免算法陷入局部最优解，将其应用于自由空间模型中的无人车路径规划中表现出优越的搜索性能。

3 改进混合遗传算法执行无人车路径规划的实现步骤

3.1 Bellman-Ford算法的实现步骤

由图1知加权连通图中共有顶点38个，从初始点S到目标点T的最短路径最多有37条边，用vi表示加权图中各个顶点，边的权值为ω(vj,vi)，其中，v1为初始点S，i,j∈[1,38]。Bellman-Ford算法的实现步骤为：

(1)初始化初始点S与每个顶点vi的路径长度dist，令dist0[S]=0,dist0[vi]=。

(2)当i=2时，从k=1到k=37时分别计算distk[vi]=min{distk-1[vi],distk-1[vk]+ω(vk,vi)}的结果，输出初始点S到顶点vi的最短路径长度dist37[vi]，并记录从初始点S行走到的最短路径上vi的前一个顶点序号，将其存储在集合Path中。

(3)令i=i+1，重复步骤(2)直至i=38，输出从初始点S到目标点T的最短路径长度dist37[T]及最短路径的顶点集合Path。

(4)对Path采用“倒向追踪”方法追溯到初始点S，获得由初始点S到目标点T的最短行走路径节点。

3.2 精英交叉机制遗传算法的实现步骤

采用Bellman-Ford算法求出的最短路径不一定是最短无碰路径，下面基于精英交叉机制遗传算法对每个粗路径点进行优化，搜索出无人车在工作空间中无碰撞行走的最佳路径，实现步骤为：

(1)个体编码方法及初始群体的确定

采用实值参数表达，用优化粗路径点的n个比例参数值来组成一系列初始路径。

(2)定义目标函数，确定适应度函数

将每条染色体对应路径的总长度定义为路径规划的目标函数，选取“界限构造法”来构造适应度函数。

(3)选择算子

将适应度最大的个体确定精英个体，采用轮盘赌方法随机选择出100条普通个体。

(4)随机交叉和精英交叉操作

首先，按交叉概率Pc随机选取20条普通个体分为10对，每对个体间随机产生一个交叉位进行单点交叉。然后按精英交叉概率Pe随机选取20条普通个体，随机设置每个个体的交叉点，以0.5的概率确定前交叉或后交叉，使精英个体的部分染色体片段复制到普通个体上。

(5)变异算子

使用逆转变异方式，按照变异概率Pm随机选取一个个体并随机设置两个逆转变异点，反向排序放置该个体两逆转点间的编码串。然后对变异个体进行编码串检验，若变异个体与精英个体完全相同，则随机生成一条个体代替变异个体。

利用精英交叉机制遗传算法优化局部最优解，通过若干代的迭代进化后搜索出环境模型中的最短路径，完成改进的混合遗传算法在自由空间模型中路径规划工作。

4 自由空间模型下无人车路径规划的仿真结果及分析

4.1 基于Bellman-Ford算法求解最短粗路径

基于已构造的自由空间模型，运行Bellman-Ford算法，仿真求出无人车在连通图中的最短路径行走路线如图2中黑色虚线所示。

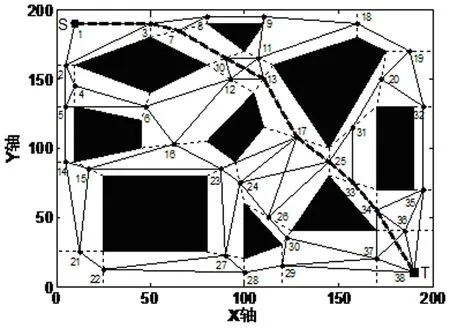
图2 Bellman-Ford算法求得最短粗路径

4.2 基于精英交叉机制遗传算法优化粗路径

分别运用基本遗传算法、保留精英策略遗传算法、及精英交叉机制遗传算法优化Bellman-Ford算法产生粗路径点，并从最优解、收敛速度和算法波动性三个方面进行了大量的仿真实验对比。

(1)最优解比较

如图3(a)、图4(a)、图5(a)中实线所示分别为基本遗传算法、保留精英策略遗传算法、及精英交叉机制遗传算法在100次仿真实验中搜索到的最短路径。三种遗传算法搜索的最短路径都比Bellman-Ford算法求解的路径更短，验证了提出的改进混合遗传算法在求解自由空间模型中最短路径问题的可行性。

图3 基本遗传算法路径规划仿真结果

图4 保留精英策略遗传算法路径规划仿真结果

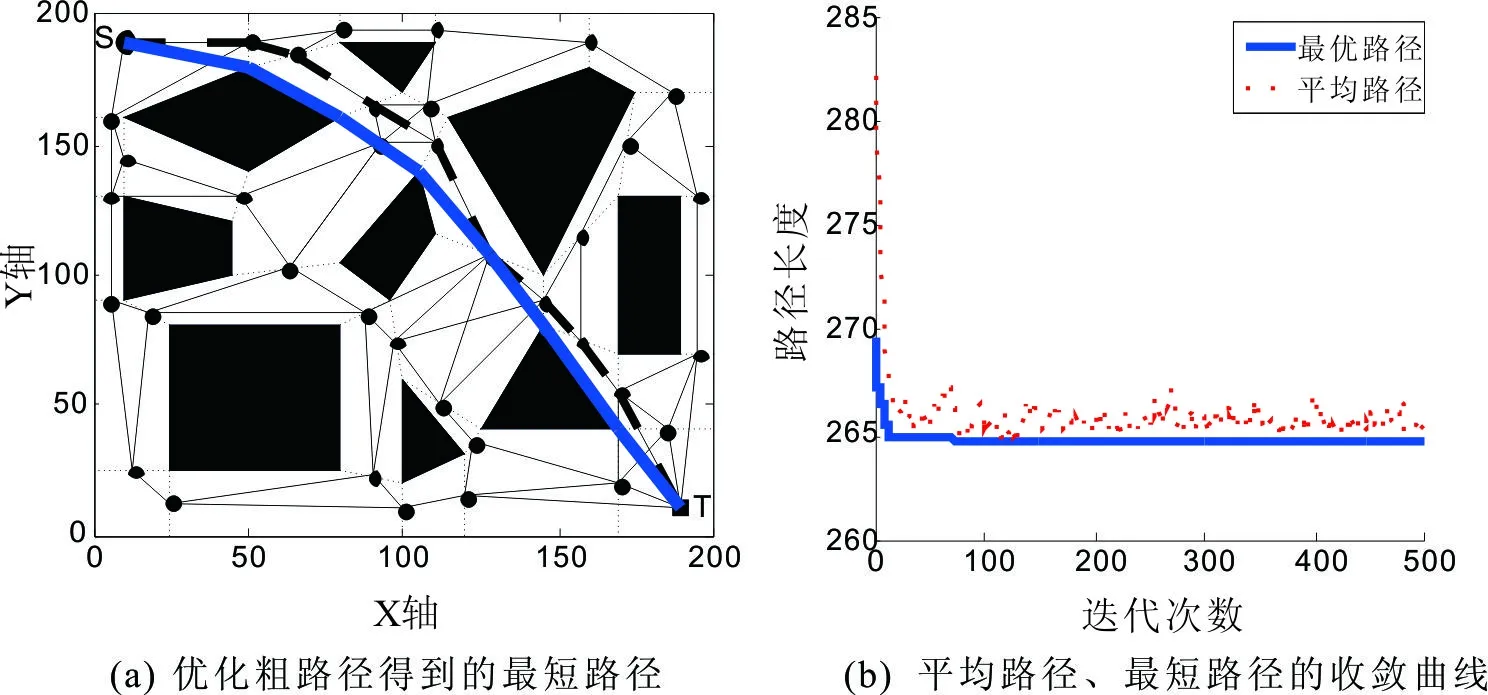
图5 精英交叉机制遗传算法路径规划仿真结果

(2)收敛速度比较

如图3(b)、图4(b)、图5(b)分别为三种算法在搜索到最优解的一次实验中迭代次数与最短路径、平均路径的收敛曲线图。分别比较三种算法最短路径和平均路径的收敛曲线，如图6、图7所示，可知精英交叉机制遗传算法产生的平均路径最小且最快趋于稳定，且仅在最短路径附近的小范围内波动。

以上分析证明，运行参数相同时精英交叉机制遗传算法收敛速度最快。

图6 三种算法的最优路径收敛曲线图

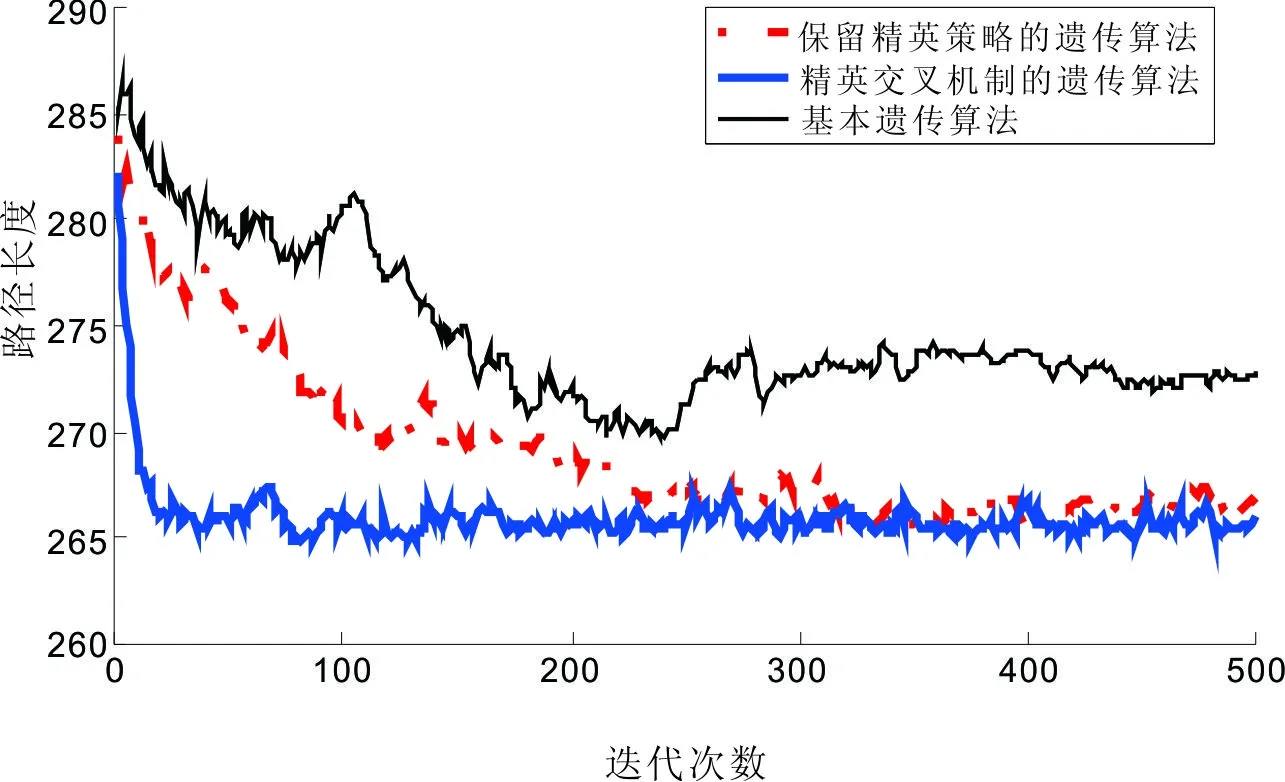
图7 三种算法的平均路径收敛曲线图

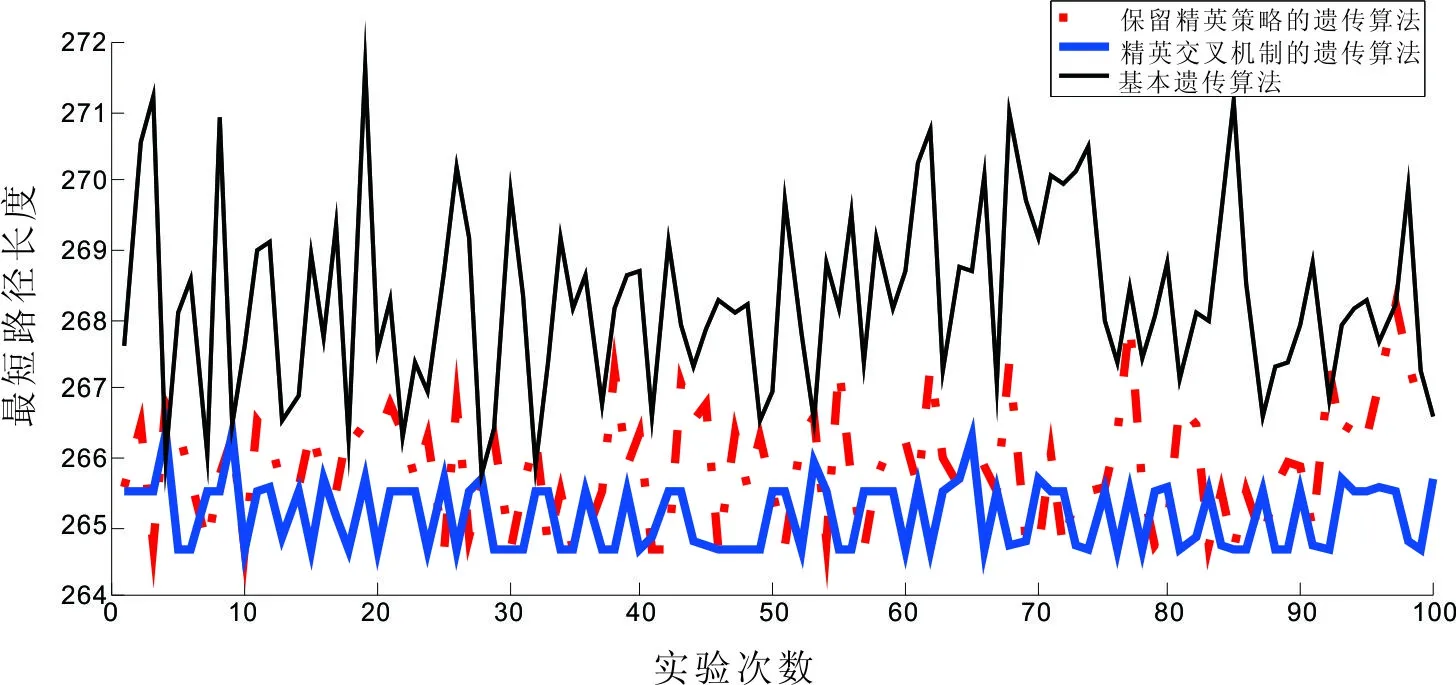
图8 三种算法在100次仿真实验中的最优解波动对比图

(3)算法的波动性比较

分析三种算法的波动性。使用相同的运行参数分别对三种算法进行100次仿真实验，记录每一次实验求出的最优解。图8是三种算法的最优解波动情况比较图，100次实验中精英交叉机制遗传算法的最优解波动范围最小，说明精英交叉机制遗传算法获得的最优解波动小，集中性高。

综上三个方面的仿真分析，验证了提出的精英交叉机制遗传算法在无人车路径规划上的可行性和高效性。

5 结 论

提出的改进混合遗传算法，将其用于搜索环境空间中最短路径，并通过仿真分析验证改进算法的高效性。依据仿真结果得到如下结论：

a.采用自由空间法构造无人车环境模型，其显著优点是无人车起始点及目标点的位置改变与构造的连通图无关。

b通过仿真实验，验证了该融合Bellman-Ford算法和精英交叉机制遗传算法的改进混合遗传算法进行无人车路径规划的可行性。

c从最优解、收敛速度和最优解波动性三个方面分析精英交叉机制遗传算法、保留精英策略遗传算法与基本算法的搜索性能，证明精英交叉机制遗传算法进行无人车路径规划时搜寻最优解的能力更强，收敛速度更快，稳定性更高。