强震作用下立体桁架结构抗连续倒塌性能研究

韩庆华， 郑靖潇， 徐 颖,3， 傅本钊

(1.天津大学 建筑工程学院，天津 300072；2.天津大学 滨海土木工程结构与安全教育部重点实验室，天津 300072；3.天津大学 水利工程仿真与安全国家重点实验室，天津 300072)

随着我国经济建设快速发展，超高层建筑、大跨空间结构、异型结构等新型结构形式不断涌现。通常该类结构人口密度较大，一旦发生连续倒塌破坏，将会造成严重的人员伤亡和财产损失。地震是对人类生产和生活危害最大且最频繁的自然灾害之一。2008年四川省汶川县发生里氏8.0级地震，5.5级以上余震9次，最大余震6.4级，绵竹县某工业厂房遭到严重破坏，屋盖整体脱落，如图1所示。2013年四川省芦山县发生7.0级地震，共发生3级以上余震103次，最大余震5.7级，芦山县体育馆网架结构损伤严重，局部杆件屈曲，导致屋面坍塌，如图2所示。

图1 绵竹县工业厂房Fig.1 Industrial plant of Mianzhu County

图2 芦山县体育馆杆件屈曲Fig.2 Member Buckling of Lushan County Stadium

结构在强震作用下的倒塌破坏模式有增量倒塌和连续倒塌两种。增量倒塌是指完整结构在不断增大的荷载作用下变形逐渐深入，结构发生成比例的整体倒塌[1]。适用于增量倒塌的分析方法包括Pushover分析和增量动力分析(Incremental Dynamic Analysis,IDA)等。Pushover分析通过对结构施加沿高度呈一定分布的水平荷载，使结构达到某一预定的标准(如顶点位移达到一定的比例，出现局部或整体的破坏等)，从而评价结构在地震作用下的弹塑性变形性能。该方法最早在1975年由Freemnan提出，90年代以后大量学者从水平加载方式、目标位移、振型参与系数等方面对该方法进行了深入研究[2-5]，该方法主要适用于框架结构。针对大跨空间结构，罗永峰等[6]采用了施加特定竖向静力荷载的Pushdown法，提出了单模态和多模态荷载模式作用下的计算方法。IDA法是将单一地震波的时程分析扩展为多条地震波的时程分析，得到多条地震波下的结构反应，进而从概率角度研究结构的反应性能参数并评估结构的抗震性能[7]。近年来国内外学者运用该方法对大跨空间结构的倒塌破坏机理进行分析[8-9]，得到了结构的破坏加速度和薄弱位置分布等结果[10]。

连续倒塌是指初始的局部破坏在构件之间发生连锁反应，最终导致与初始局部破坏不成比例的结构大范围或整体的倒塌[11]。何庆峰等[12]采用有限元软件LS-DYNA对于冲击荷载下钢筋混凝土框架结构的抗连续倒塌性能进行研究。程小卫等[13]采用拆除构件法对于基于多尺度模型的RC框架的撞击倒塌响应进行了分析。目前最普遍采用的连续倒塌分析方法是备用荷载路径法(Alternative Path Method,AP)。该方法通过将结构中的构件“移除”，来模拟局部破坏，分析剩余结构的应力重分布能力，判断结构是否会发生倒塌。国内外学者采用AP法对大跨空间结构的抗连续倒塌性能进行了大量的研究[14-16]，但以上研究大多只考虑了结构在静力荷载作用下的抗连续倒塌性能。

目前针对强震作用下大跨空间结构抗倒塌性能的研究大多选取完好结构为研究对象[17-20]，假定结构发生增量倒塌破坏，而针对由初始局部破坏引起的连续性倒塌研究相对较少。以往的震害事故表明，主震之后通常伴有多次余震，主震过程可能引起大跨空间结构薄弱部位杆件发生初始失效，并导致结构在余震过程中发生连续倒塌破坏。同时结构在日常使用过程中由于锈蚀、爆炸、火灾、冲击等因素，也可能产生初始破坏[21]，导致结构在地震过程中发生连续倒塌破坏。因此，对大跨空间结构在地震作用下的抗连续倒塌性能展开研究具有重要意义。

本文将IDA法与AP法相结合，研究了立体桁架结构在强震作用下的抗连续倒塌性能。首先通过IDA分析，得到了地震作用下完整立体桁架结构的破坏加速度和倒塌极限位移，并得到了结构薄弱位置分布规律。然后采用AP法分别选择主桁架跨中上弦杆和下弦杆以及跨中一榀支撑桁架的上弦杆作为初始失效构件，采用预定义场引入初始失效构件，考虑了损伤累积效应带来的结构刚度退化，分析了不同破坏模式下立体桁架的连续倒塌破坏机理。最后提出了改进立体桁架结构抗连续倒塌性能的有效措施，为该类结构抗连续倒塌设计提供指导。

1 完整结构的动力响应

1.1 数值分析模型

以天津某大学体育馆钢结构屋盖为例，建立数值分析模型，如图3所示，主桁架采用倒三角截面，横向跨度为36 m，高度为3 m，主桁架纵向间距为8.5 m，设三榀平面桁架作为平面外支撑体系，主桁架两端为固定铰支座。所有杆件均选用Q235钢，主桁架杆件的截面尺寸如表1所示，杆件材料如表2所示，采用考虑损伤累积效应和杆件受压屈曲[22]的弹塑性钢材本构模型。采用ABAQUS动力显式方法，对结构进行动力非线性分析。桁架弦杆采用BEAM单元，腹杆采用TRUSS单元。结构重力荷载代表值以MASS单元形式施加在上弦节点上，其中恒荷载按1.0 kN/m2，活荷载按0.5 kN/m2计算。结构设计地震分组为第一组，场地类别为Ⅲ类，特征周期Tg=0.45 s，计算过程中采用Rayleigh阻尼，阻尼比取0.02。

表1 主要杆件截面尺寸Tab.1 Member specifications of spatial truss mm

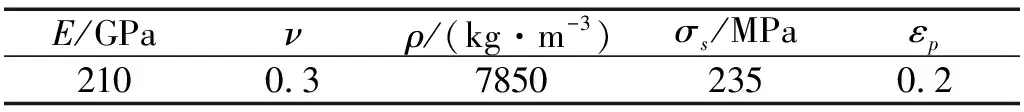
表2 杆件材料性能参数Tab.2 Material properties of components

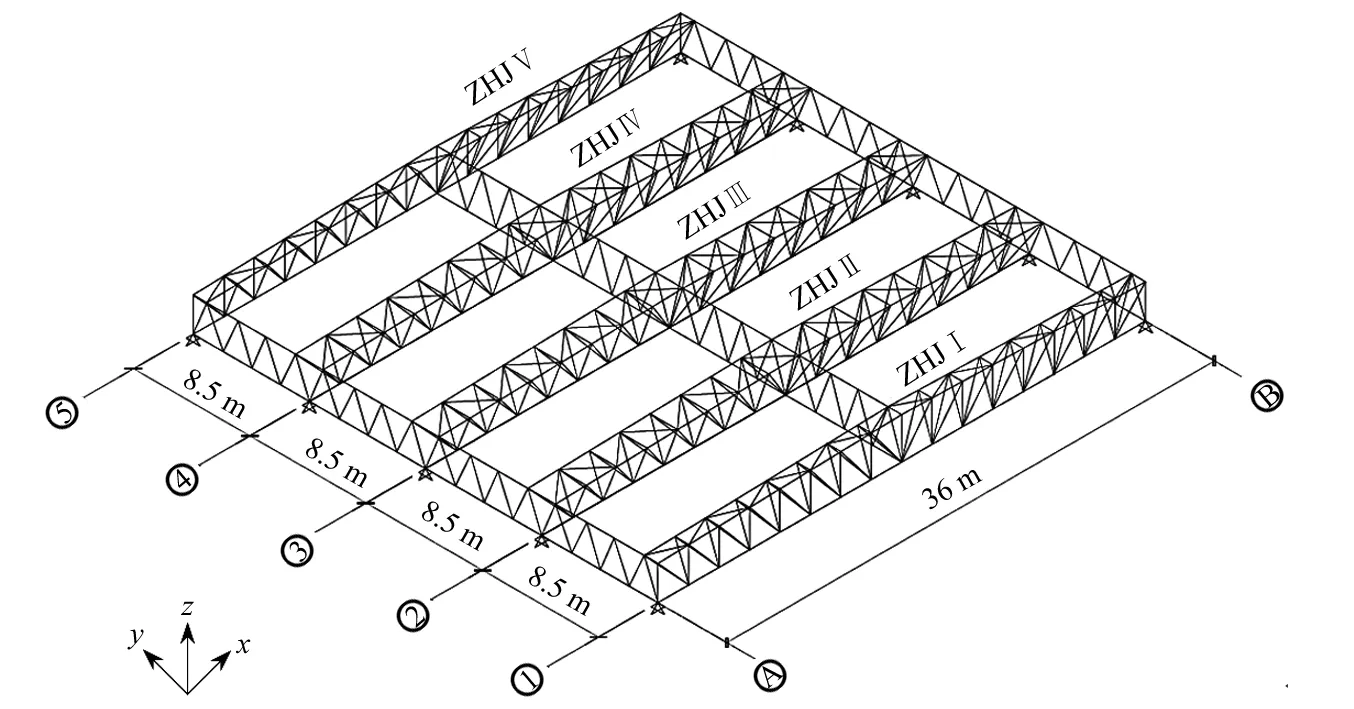
图3 立体桁架计算模型Fig.3 Calculation model of the spatial truss structure

1.2 地震动输入

对完整结构进行动力非线性分析，依次输入多条地震记录并逐级增大地震波峰值加速度(PGA)，直至结构发生倒塌破坏。中国《建筑抗震设计规范》[23]中规定，采用时程分析法时，应按建筑场地类别和设计地震分组选用实际强震记录和人工模拟的加速度时程曲线，其中实际地震记录的数量不应少于总数的2/3。在选择地震波时，峰值加速度(Pake Ground Acceleration,PGA)太大或太小的不予考虑，然后根据反应谱卓越周期选出适应场地的地震波，根据结构基本周期在相应频段上选择拟合最好的3条地震波。本文选取宁河波、El-Centro波以及人工波，采用三向输入的方式，地震动参数见表3。人工波特征周期Ts=0.45 s，持时为20 s，增强时间T1=5 s，衰减时间T2=10 s，三向峰值加速度比值为X∶Y∶Z=0.85∶1∶0.65。

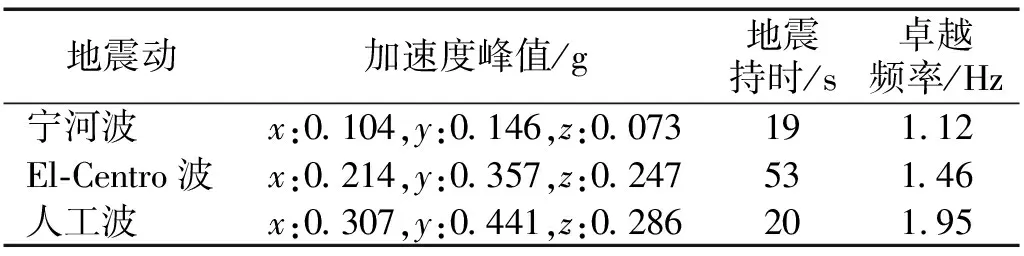
表3 地震激励参数Tab.3 Parameters of seismic ground motions

1.3 破坏加速度及倒塌极限位移

采用增量动力法，根据结构的动力响应对地震动进行8～10次调幅，弹性阶段按步长0.05 g～0.1 g调幅，当接近破坏极限时，按步长0.01 g调幅。在三条地震波作用下，立体桁架结构跨中下弦节点竖向位移随PGA变化规律、塑性杆件所占比例随PGA变化规律以及总应变能见图4～图6。当曲线偏离平衡位置，即PGA的微小增量导致响应参数的大幅增加时，认为结构发生倒塌破坏。

在宁河波作用下，当PGA达到600 gal～610 gal时，跨中下弦节点竖向位移发生明显转折(图4)，塑性杆件所占比例从16.5%增加到37.6%(图5)，同时结构总应变能异常增大(图6a)。因此在宁河波作用下，结构的破坏加速度峰值为600 gal。同理，在El-Centro波及人工波作用下，结构所能承受的最大峰值加速度分别为620 gal和660 gal。

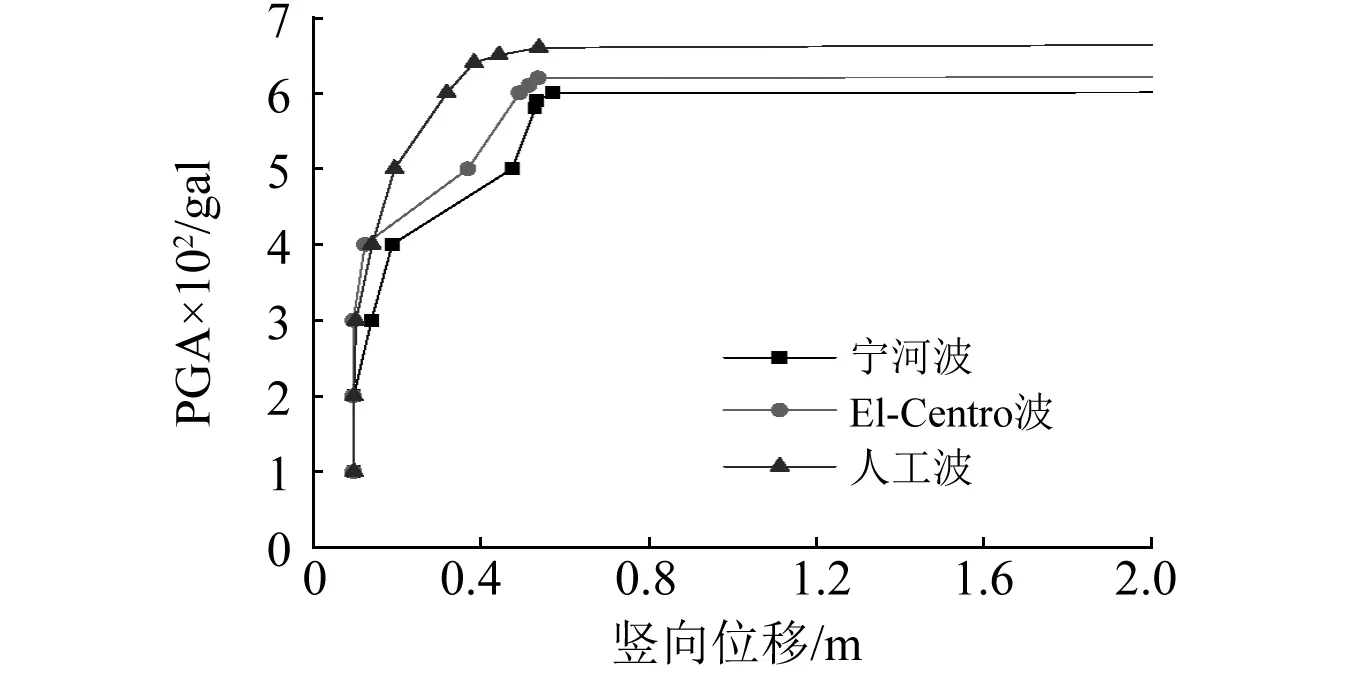
图4 完整结构的跨中下弦节点竖向位移随PGA变化曲线Fig.4 Vertical displacement versus PGA curve of the joint of lower chord in midspan of the original structure

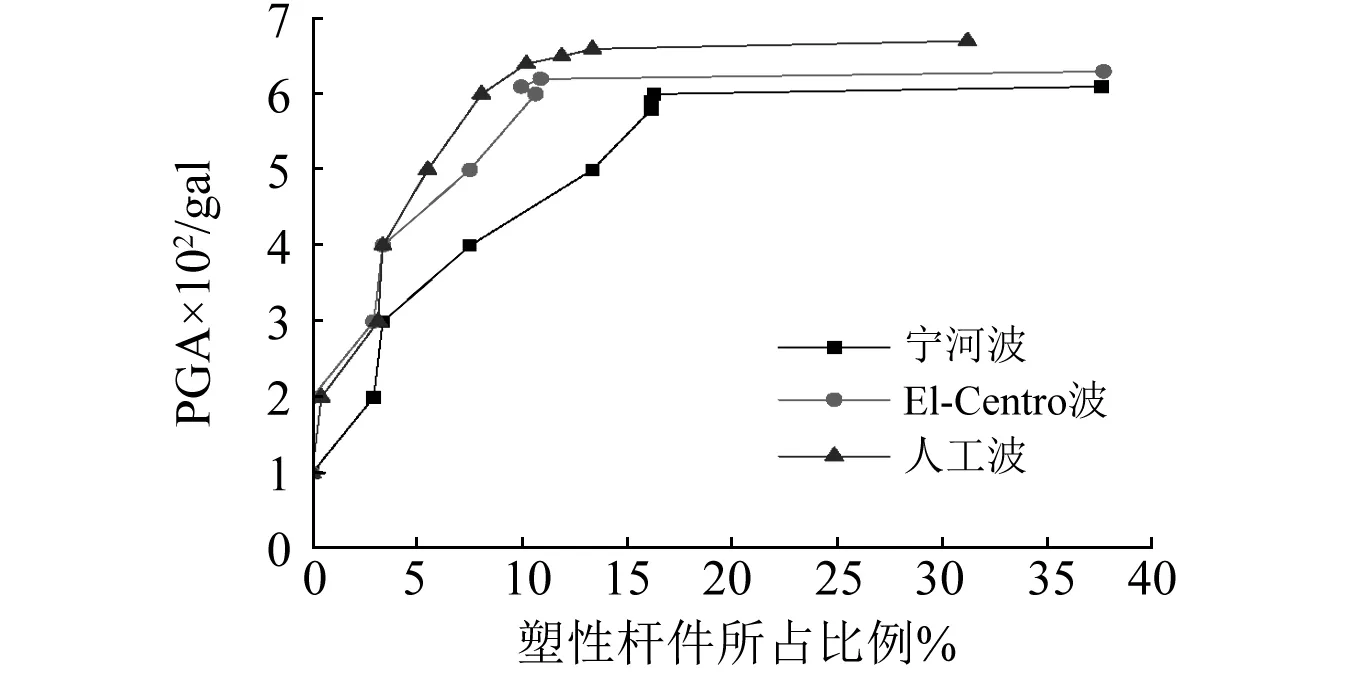
图5 完整结构的塑性杆件比例随PGA变化曲线Fig.5 Yield element ratio versus PGA curve in the original structure

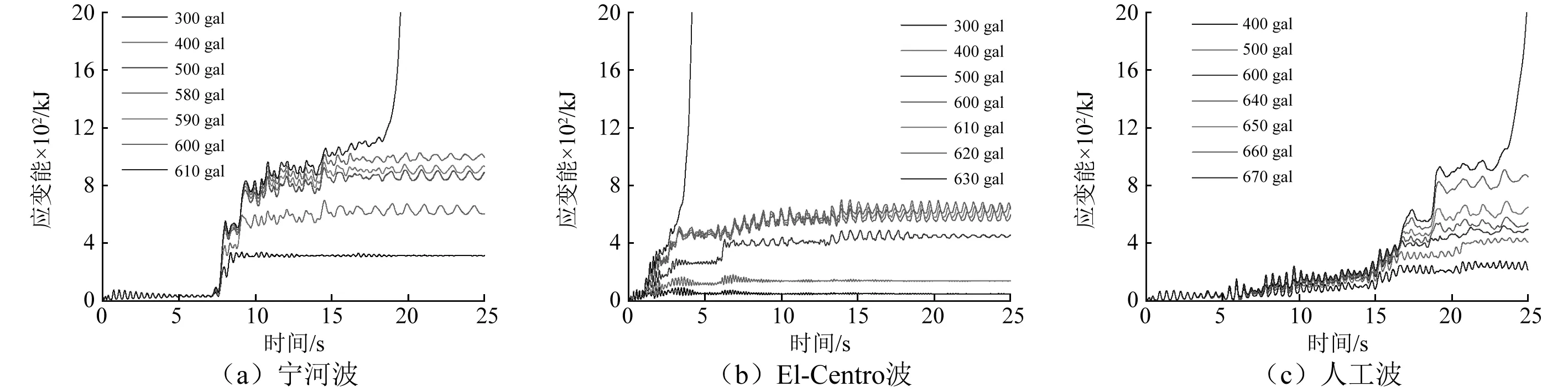
图6 完整结构的总应变能时程曲线Fig.6 Time history curve of the strain energy in the original structure

取破坏加速度作用下立体桁架跨中下弦节点竖向位移最大值，作为结构的倒塌极限位移，在不同地震波下的倒塌极限位移如表4所示。

表4 完整结构破坏加速度及倒塌极限位移Tab.4 Ultimate acceleration & ultimate displacement of the original structure

1.4 薄弱部位分布

从结构塑性发展的角度考虑，进入塑性杆件的比例反映了结构的塑性变形程度。在宁河波作用下，当达到破坏加速度时，共16.3%杆件进入塑性；在El-Centro波和人工波作用下，当达到破坏加速度时，进入塑性杆件比例分别为10.9%和13.4%。计算结果表明在三条地震波作用下，结构进入塑性的杆件位置基本相同，主要为主桁架跨中3/8L范围内的上弦杆、下弦杆及主桁架Ⅱ和Ⅳ之间的跨中支撑桁架上弦杆。其中，主桁架上弦杆和支撑桁架上弦杆受压，发生动力失稳破坏；主桁架下弦杆受拉，发生动力强度破坏。在宁河波作用下，结构的等效塑性应变云图见图7。

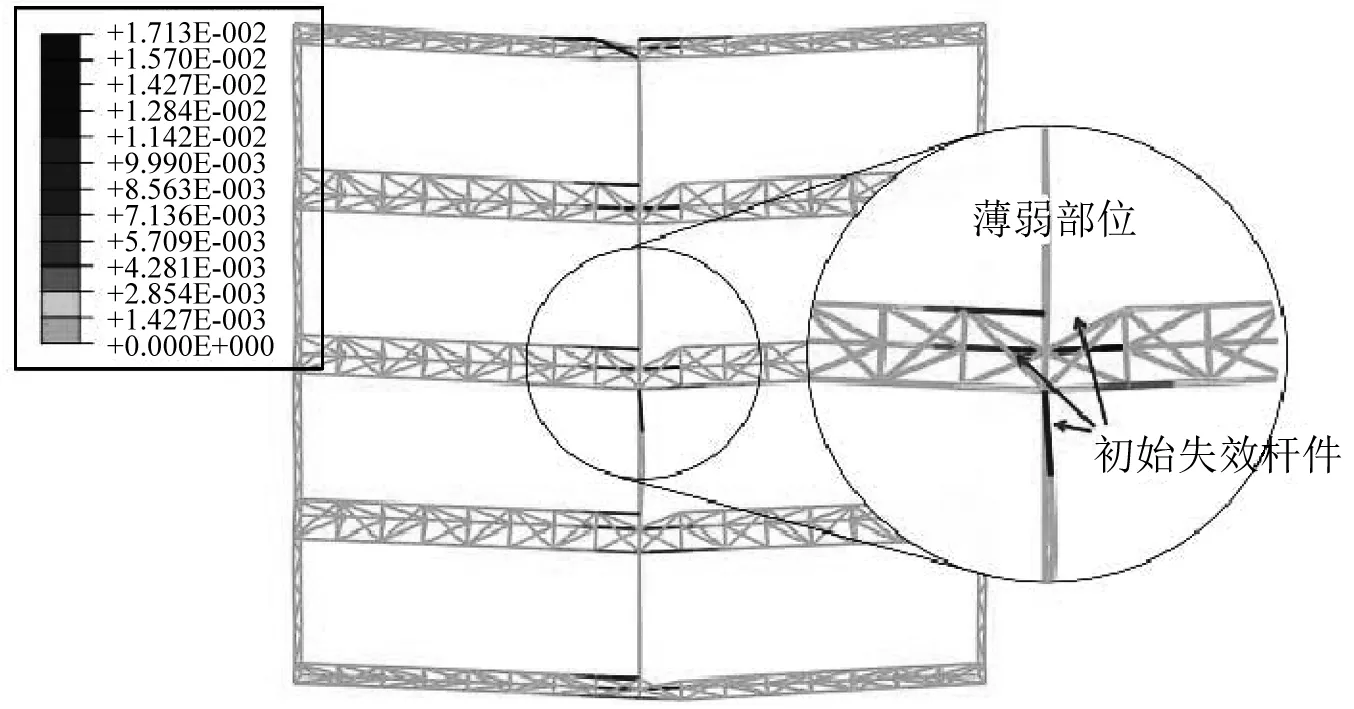
图7 等效塑性应变云图Fig.7 Equivalent plastic strain nephogram

2 地震作用下立体桁架结构连续倒塌破坏

2.1 缺陷结构的连续倒塌破坏模式

在动力荷载作用下，立体桁架结构可能发生动力失稳破坏或者动力强度破坏[22]。若发生动力失稳破坏，则结构内部塑性发展较浅，结构变形在达到破坏加速度时突然增大，主桁架发生平面内或平面外失稳；若发生动力强度破坏，则结构内部塑性发展较为深入，结构变形随峰值加速度的增大不断增加，直到主桁架主要受力构件全部失效产生平面内强度破坏。

由1.4节分析可知，完整结构在地震作用下的薄弱部位为主桁架跨中3/8L范围内的上弦杆、下弦杆及跨中支撑桁架的上弦杆。从这三类杆件中分别选取等效塑性应变最大的杆件作为初始失效杆件(图7)，对结构进行连续倒塌分析，步骤如下：①对完整结构进行静力分析，保存结构的应力场和应变场；②建立缺陷结构的几何模型，在ABAQUS中设置预定义场，从而引入初始失效构件，此时结构处于力的不平衡状态；③输入地震波并逐级增大PGA，对缺陷结构进行强震作用下的动力显式分析。

以三向宁河波为例，逐级增大峰值加速度，得到三类缺陷结构跨中下弦节点竖向位移及进入塑性杆件比例随PGA的变化规律如图8、9所示，结构总应变能时程曲线如图10所示。表5列出了选取不同初始失效构件时，立体桁架结构的破坏加速度及倒塌极限位移。

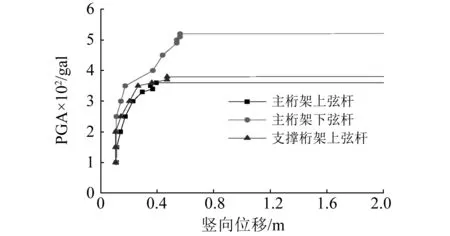
图8 缺陷结构的跨中下弦节点竖向位移随PGA变化曲线Fig.8 Vertical displacement versus PGA curve of the joint of lower chord in midspan of the damaged structure

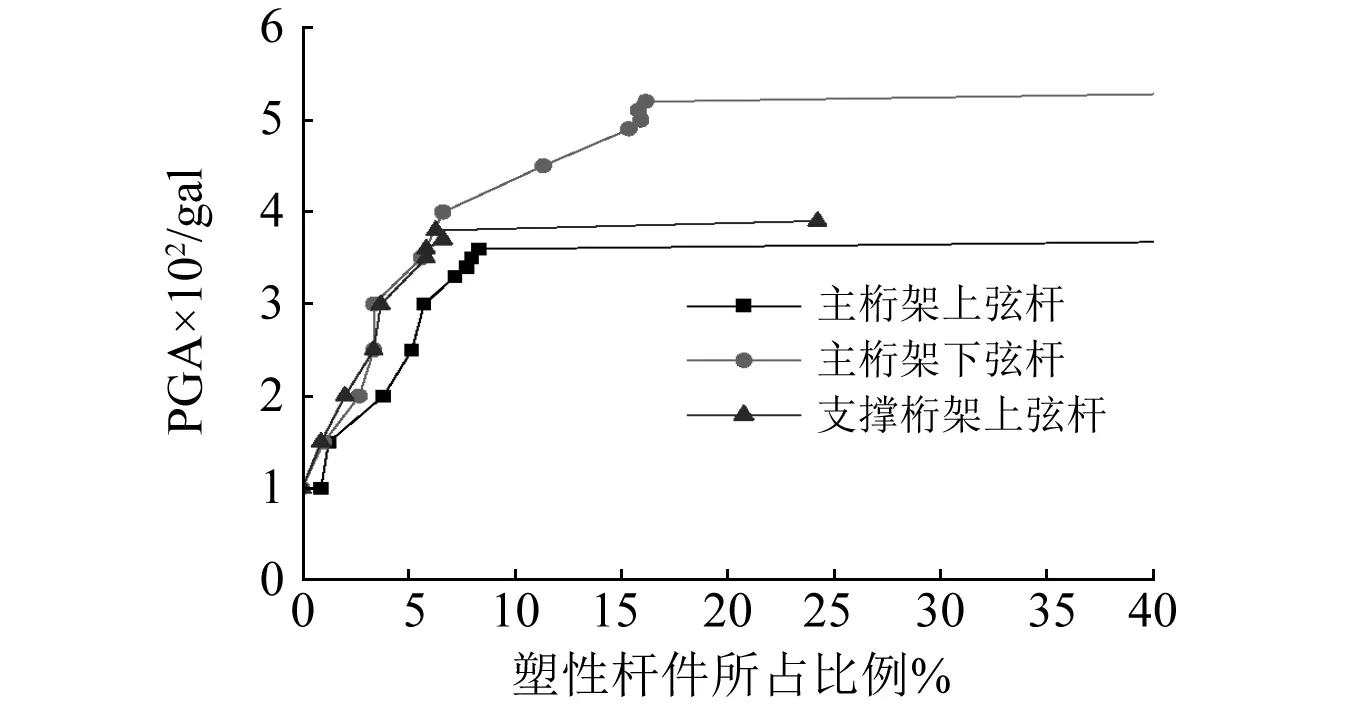
图9 缺陷结构的塑性杆件比例随PGA变化曲线Fig.9 Yield element ratio versus PGA curve in the damaged structure

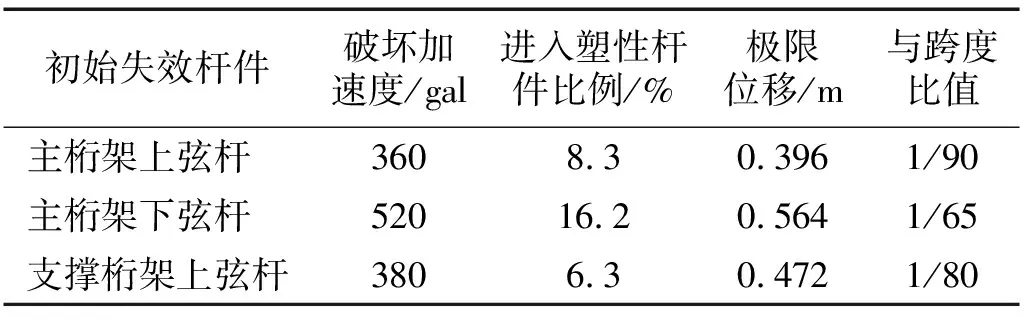
初始失效杆件破坏加速度/gal进入塑性杆件比例/%极限位移/m与跨度比值主桁架上弦杆3608.30.3961/90主桁架下弦杆52016.20.5641/65支撑桁架上弦杆3806.30.4721/80

如图8所示，当主桁架上弦杆发生初始失效时，结构破坏加速度为360 gal，跨中下弦节点竖向位移在达到极限位移0.396 m后迅速增大；进入塑性杆件的比例从8.3%增加到50%以上；应变能曲线急剧上升(图10(a))。当主桁架下弦杆发生初始失效时，PGA由520 gal增加到530 gal，跨中下弦节点竖向位移在达到0.564 m后迅速增大，进入塑性杆件的比例从16.2%增加到45.9%，总应变能迅速增大(图10(b))；同理，当支撑桁架上弦杆发生初始失效时，破坏加速度为380 gal，极限位移为0.472 m，破坏加速度作用下进入塑性杆件的比例为6.3%，之后总应变能异常增大(图10(c))。从表5可知，缺陷结构的破坏加速度较完整结构降低了13.3%～40.0%，倒塌极限位移降低了1.6%～30.9%，同时进入塑性杆件的比例降低了0.6%～61.3%。以上分析进一步说明，在强震作用下，结构由于初始构件失效发生的连续倒塌破坏比通常认为的增量倒塌破坏更加危险。

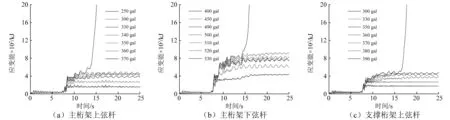
图10 缺陷结构的总应变能时程曲线Fig.10 Time history curve of the strain energy in the damaged structure

图11为不同初始失效杆件对应的结构变形图。当主桁架上弦杆发生初始失效时，主桁架Ⅲ产生了明显的侧向失稳同时下挠严重。结构发生倒塌破坏前塑性发展较浅，进入塑性杆件比例不超过10%，相比于完整结构倒塌极限位移下降了30.9%，最终发生动力失稳破坏(图11(a))。当主桁架下弦杆发生初始失效时，下挠最严重的为主桁架Ⅲ、Ⅳ、Ⅴ，各榀主桁架产生对称变形。结构发生倒塌破坏前塑性发展深入，塑性杆件比例超过10%，为16.2%，较完整结构倒塌极限位移仅下降1.6%，最终发生动力强度破坏(图11(b))。当支撑桁架上弦杆发生初始失效时，主桁架Ⅱ发生了平面外失稳，下挠最严重的为主桁架Ⅱ、Ⅲ之间的支撑桁架。结构发生倒塌前塑性发展较浅，塑性杆件比例不超过10%，较完整结构倒塌极限位移降低了17.6%，最终发生动力失稳破坏(图11(c))。

在上述初始失效构件中，主桁架上弦杆与支撑桁架上弦杆为受压杆件，主桁架下弦杆为受拉杆件。当受压杆件发生初始失效时，相邻杆件应力迅速增大，失稳区域进一步扩大，结构塑性发展较浅，最终发生整体失稳破坏；当受拉杆件发生初始失效时，相邻杆件应力重分布过程缓慢，结构塑性发展深入同时产生较大的变形，破坏加速度较发生动力失稳破坏时增大了36.8%～44.4%，倒塌极限位移增大19.5%～42.4%。因此，对立体桁架结构进行抗连续倒塌设计时，应首先对上述薄弱位置的受压杆件进行加强，并通过有效手段阻止局部失稳的进一步传播。

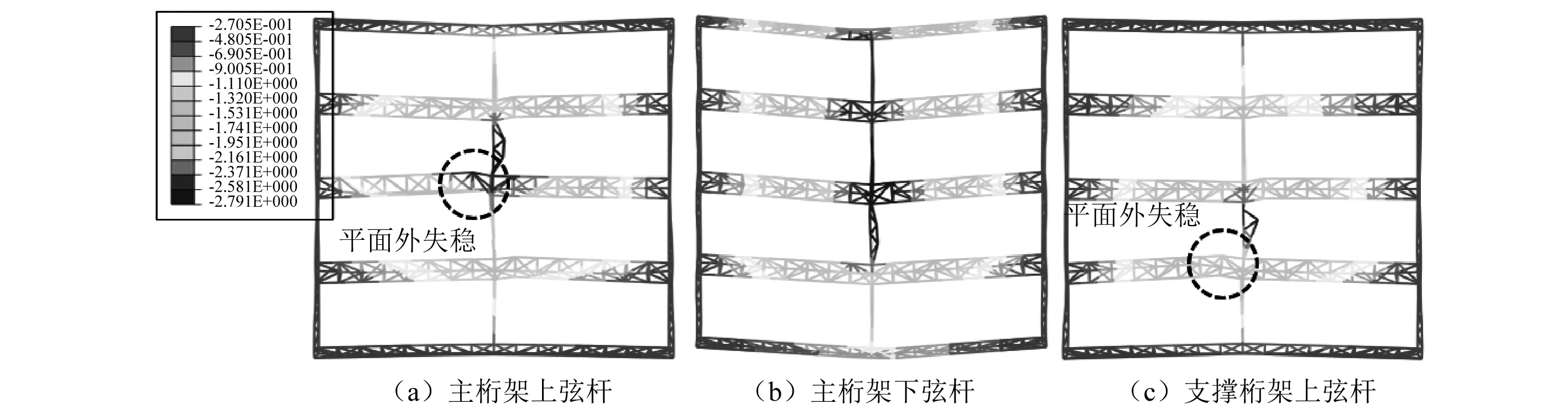
图11 缺陷结构不同初始失效杆件对应的结构变形图Fig.11 Structural deformation of the damaged structure with different initial failure member

2.2 增加交叉支撑后的连续倒塌破坏模式

为了防止受压杆件发生初始失效后，局部失稳的进一步传播，在上述模型跨中3/8L范围内的上弦平面设置交叉支撑，截面尺寸为Φ140×6，支撑长度为9.3 m，采用CABLE单元，计算模型如图12所示。增加侧向支撑后，结构静力响应较原结构变化很小，杆件应力最多减小了7%，节点竖向位移减小了8%。选择与2.1节相同的初始失效构件，并输入三向宁河波，得到结构跨中下弦节点竖向位移及进入塑性杆件比例随PGA的变化规律如图13、14所示。

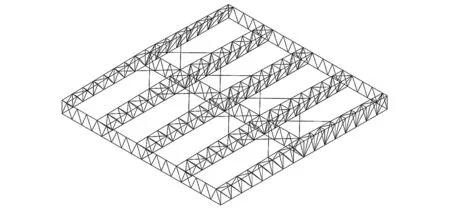
图12 增加侧向支撑的计算模型Fig.12 Calculation model after adding cross diagonal bracings

设置交叉支撑后，结构的动力响应如表6所示。当主桁架跨中上弦杆和支撑桁架上弦杆为初始失效杆件时，由于交叉支撑的拉结作用，有效抑制了主桁架的平面外失稳，结构的整体性增强。结构破坏加速度分别增加了69.4%和73.7%，进入塑性比例分别增大了80.7%和88.9%，结构塑性发展深入，内力重分布更加充分，转而发生动力强度破坏。由于结构整体刚度的增加，连续倒塌极限位移分别降低了36.9%和28.4%，为结构跨度的1/145和1/110。

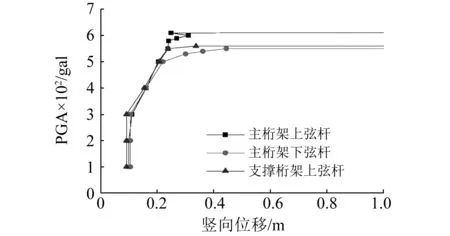
图13 增加交叉支撑后跨中下弦节点竖向位移随PGA变化曲线Fig.13 Vertical displacement versus PGA curve of the joint of lower chord in midspan after adding cross diagonal bracings

当主桁架下弦杆为初始失效杆件时，破坏加速度增大5.8%，塑性杆件比例增加3.7%，结构连续倒塌极限位移为跨度的1/80，仍发生动力强度破坏。由于结构倒塌破坏模式较原结构未发生改变，因此结构动力响应变化不大。

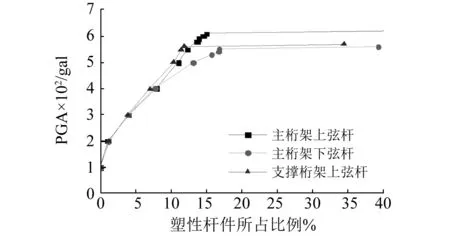
图14 增加交叉支撑后塑性杆件比例随PGA变化曲线Fig.14 Yield element ratio versus PGA curve after adding cross diagonal bracings

图15为增加交叉支撑后，结构发生连续倒塌破坏时的变形图。可以看出，交叉支撑有效地限制了主桁架的侧向变形，主桁架仅产生平面内下挠，同时跨中支撑桁架产生了较大变形，后续失效杆件主要为主桁架跨中下弦杆、跨中支撑桁架下弦杆以及与交叉支撑相邻的主桁架上弦杆。

综上，针对初始失效构件为受压杆件的两种情况，增加侧向交叉支承可以有效提高结构的抗连续倒塌性能，结构最终发生动力强度破坏。与动力失稳破坏相比，塑性发展更加充分，破坏加速度明显提升。

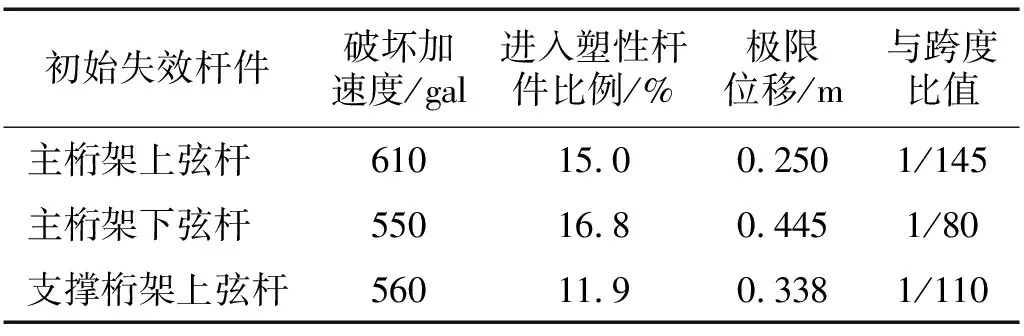
表6 增加侧向支撑后结构动力响应Tab.6 Dynamic responses of structure after adding cross diagonal bracings

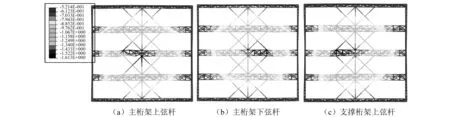
图15 增加交叉支撑后不同初始失效杆件对应的结构变形图Fig.15 Structural deformation of the structure with different initial failure member after adding cross diagonal bracings

3 结 论

本文采用预定义场法引入初始失效杆件，分析了立体桁架结构在强震作用下的连续倒塌破坏机理和破坏模式，分析了不同初始失效下该类结构破坏加速度、倒塌极限位移等响应的变化规律，提出了改善结构抗连续倒塌性能的有效措施。主要结论如下：

(1)完整结构在强震作用下的破坏加速度为600～660 gal，倒塌极限位移为结构跨度的1/65～1/60，薄弱位置为主桁架跨中3/8L范围内的上弦杆、下弦杆及跨中支撑桁架上弦杆。

(2)分别选取主桁架跨中上弦杆、下弦杆及跨中支撑桁架的上弦杆为初始失效构件，对结构进行连续倒塌分析。缺陷结构的破坏加速度较完整结构降低了13.3%～40.0%，倒塌极限位移降低了1.6%～30.9%。在强震作用下，结构由于初始构件失效发生的连续倒塌破坏比常规的增量倒塌破坏更加危险。

(3)当初始失效杆件为受压杆件时，结构产生动力失稳破坏；当初始失效杆件为受拉杆件时，结构产生动力强度破坏，后者破坏加速度增大36.8%～44.4%，倒塌极限位移增大19.5%～42.4%。对立体桁架结构进行抗连续倒塌设计时，应首先对薄弱位置的受压杆件进行加强，并通过有效手段阻止局部失稳的进一步传播。

(4)针对发生动力失稳破坏的立体桁架结构，增加侧向交叉支撑可以有效提高结构的抗连续倒塌性能，破坏模式转变成动力强度破坏，破坏加速度提高69.4%～73.7%。同时由于结构整体刚度的增加，连续倒塌极限位移降低了28.4%～36.9%。