基于EWT及模糊相关分类器的管道微小泄漏检测

肖启阳， 李 健， 孙洁娣， 曾周末

(1. 天津大学 精密测试技术与仪器国家重点实验室，天津 300072； 2. 燕山大学 信息科学与工程学院，河北 秦皇岛 066004)

随着清洁能源天然气的需求日益增长，燃气管道建设也随之飞速发展。但由于种种自然或人为原因导致管道微小泄漏事故时有发生，甚至造成巨大的经济损失和人员伤亡[1-4]。为保障管道安全运行，开展对管道微小泄漏检测研究具有重要意义。目前，常用的管道泄漏检测装置主要通过管道输送压力、流量等参数的变化来判断．该类方法易受输送物质特性及输送工况等诸多因素影响[5-7]。声发射技术是通过判断声发射源特性(如缺陷类型、大小、位置等)来实现动态无损检测，该技术具有灵敏度高、可全天候实时检测等优点[8-10]。为此，文中采用声发射技术对天然气管道进行微小泄漏检测。

管道发生微小泄漏时，周边环境复杂，噪声干扰多，且采集的信号具有非平稳特性，有必要对采集的信号进行去噪处理，提取微弱信号特征[11]。近年来，针对非平稳信号去噪，多数研究成果通常采用非平稳信号处理方法对信号进行分解，然后利用阈值去除噪声分量，提取出无噪分量[12-14]。然而这些方法都依赖于阈值的设置，不具有自适应性。经验小波变换(Empirical Wavelet Transform, EWT) 是2013年提出的一种非平稳信号处理方法[15]。与EMD分解相比，EWT是在小波框架内对信号进行处理，因此，EWT理论充分，分解过程中避免EMD方法产生的模态混叠现象，可以提取信号的固有模态[16]。针对传感器采集的非平稳信号，本文提出基于EWT的自适应降噪法对采集信号进行处理，提取主要成分，自适应去除噪声干扰。

模糊函数是一种经典时频分析工具，它在非平稳信号分析与处理理论中具有重要作用，已经被广泛应用于雷达信号分析与处理、光学信息处理、声纳技术等领域[17-18]。然而，模糊函数存在交叉项干扰，难以提取信号的时频特征。针对这一不足，利用相关系数构造模糊函数相关分类器，既可以降低计算量，又可以避开交叉项的干扰。采用模糊相关分类器识别不同类型的振动信号，实现管道微小泄漏检测。

针对天然气管道微小泄漏，本文提出基于经验小波变换及模糊相关分类器的管道泄漏检测方法。首先对采集的信号进行EWT分解，根据峭度提出基于EWT的自适应降噪法，然后对提取的无噪声分量进行重构获得降噪信号，根据信号的模糊特性提出模糊相关分类器对重构后不同类型的信号进行训练与测试，实验结果表明，该方法能够对管道微小泄漏进行检测，且识别率较高。

1 EWT原理

Gilles等于2013年提出的一种新的自适应信号处理方法—经验小波变换，该方法是通过对信号的频谱自适应分割获得一系列的调频调幅信号[15-16]。对于任意复杂信号f(t)，分解后的数学表达式：

(1)

式中：fk(t)为分解后的分量,fk(t)被定义为调频调幅信号。

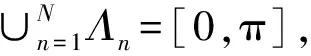
(2)

(3)

式中：

τn=γωn

(4)

β(x)=x4(35-84x+70x2-20x3)

(5)

(6)

采用传统的小波变换来构造EWT，假设F[·]和F-1[·]分别为傅里叶变换及其反变换。则经验小波高频成分由信号和经验小波函数内积得到，其数学表达式如下：

(7)

那么低频成分可通过求取信号和经验尺度函数内积获得，数学表达式如下：

(8)

利用高频成分和低频成分获得重构原信号，其数学表达式如下：

(9)

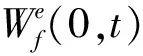
(10)

(11)

通过经验小波变换实现复杂信号的自适应分解，获取一系列的调频调幅分量，对这些分量处理获取瞬时频率和瞬时幅值。

2 基于EWT自适应降噪法及仿真

2.1 基于EWT自适应降噪法

传感器采集的信号中常常含有噪声干扰，导致泄漏特征不明显，因此，为了准确提取特征信息，需要对经EWT分解后的分量进行处理，降低噪声干扰，提高信噪比[13]。目前，多数学者采用阈值法对信号进行处理，该方法将分解后的分量分为噪声分量和无噪声分量，通过阈值选取无噪声分量。然而阈值选取普遍采用人为设置，不具有自适应性[14]。峭度是反映振动信号分布特性的数值统计量，对冲击信号敏感，可应用于振动信号去噪。研究表明泄漏信号中主要成分为冲击成分，而其他成分则可认为是干扰噪声信号，为此根据峭度自适应的选取包含冲击成分的分量，降低噪声干扰，提高信噪比。基于EWT的自适应选择算法具体步骤如下：

(1) 计算信号x(t)经EWT分解后分量的峭度值μn

(12)

式中：N为采样点数;cnk是EWT分解后的分量

(2) 根据μn得到：

μ={μn},n=1,2,…,N

(13)

(3) 定义信号x(t)的调频调幅分量的峭度因子Zn：

(14)

(4) 根据峭度因子选择峭度分量

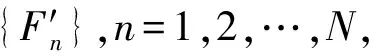
(5) 求出相邻两个调频调幅分量峭度因子之差，之后找出最大差值。

(15)

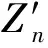
2.2 算法仿真

为了验证算法的有效性，文中采用仿真信号进行

分析，仿真信号由调频调幅信号和随机白噪声组成，仿真信号的数学表达式如下

x1(t)=
[1+0.3cos(10πt)]sin[200πt+sin(15πt)]

(16)

x2(t)=cos[60πt+sin(10πt)]

(17)

x(t)=x1(t)+x2(t)+0.4randn

(18)

t=[0,0.4]

(19)

对仿真信号进行EWT分解，计算分解后的峭度值，分解后的结果如图1所示，分解后不同分量的峭度值如图2所示。

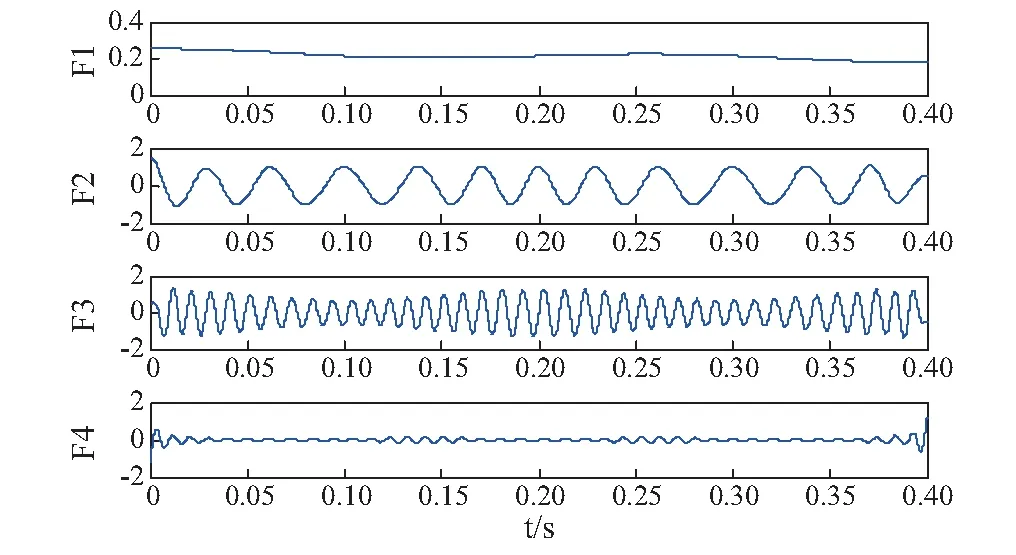
图1 仿真信号经EWT分解结果Fig.1 EWT result of simulated signal

按照上文所述方法计算不同分量的峭度因子，并进行排序，排序前后不同分量的峭度因子如图3所示。

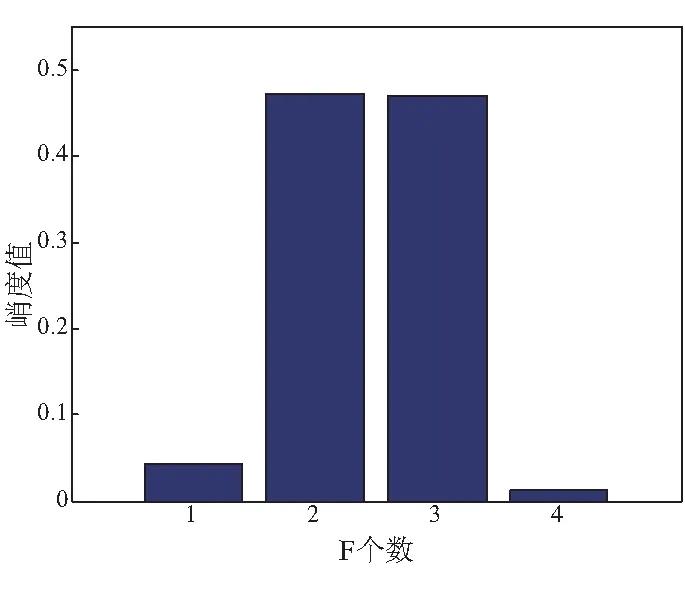
图2 分解后不同分量的归一化峭度值Fig.2 Normalized kurtosis of different components

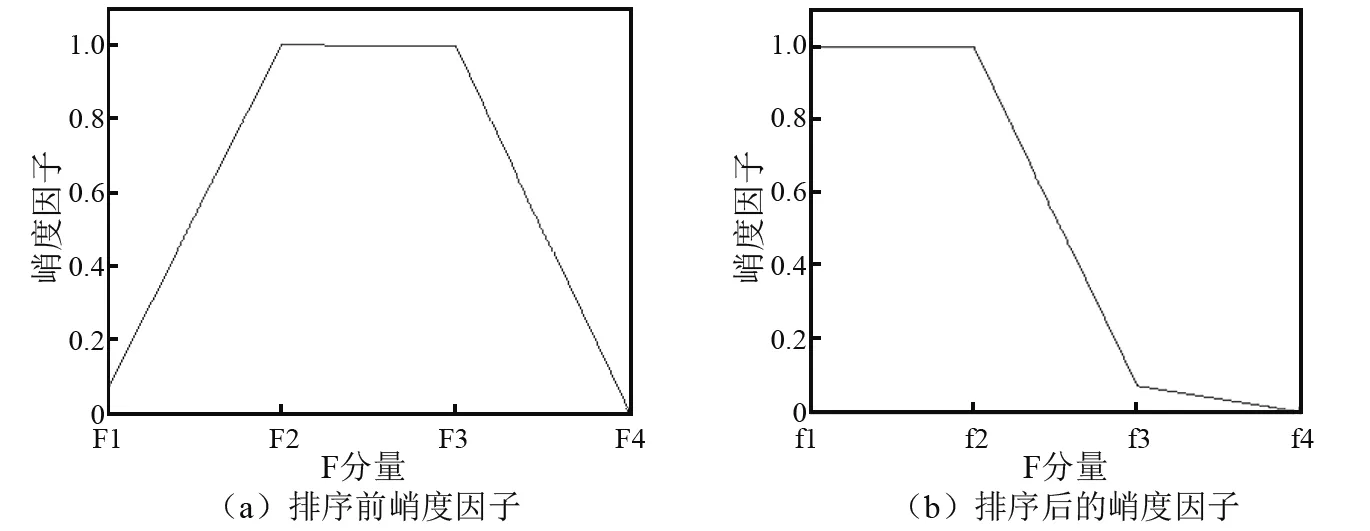
图3 排序前后的峭度因子Fig.3 Kurtosis factors before sorting and after sorting

观察图3可得，排序后两个峭度因子之差最大值位于F2和F1之间，最大值为0.929 8，因此，F2和F3分量包含主要峭度成分，F1和F4分量为噪声成分。由仿真信号表达式可得，F2和F3对应调频调幅信号。由于随机白噪声符合正态分布规律，为此对四个分量进行正态分布验证，结果如图4所示。

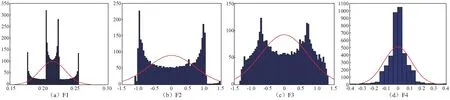
图4 四个分量的正态分布图Fig.4 Histograms of F1-F4

观察图4可得，F1和F4的直方图与正态分布曲线吻合，表明F1和F4分量近似符合正态分布规律，F1和F4分量主要为噪声分量，由此表明，基于EWT的自适应降噪法可以有效去除噪声干扰，提取了信号的冲击成分。

均方误差(MES)和信噪比(SNR)经常被用来评价降噪效果，因此，分别计算基于EMD和基于EWT降噪前后信号的均方误差和信噪比，结果如表1所示。

表1 仿真信号的均方误差和信噪比

表1中降噪后的信噪比越大，均方误差越小，表明降噪效果越好。通过对比两种降噪方法，由于EMD分解过程中存在模态混叠现象，导致降噪效果较差，基于EWT降噪法能够有效的对非平稳信号进行分解，获取正确的分量，降噪效果较好。

3 模糊相关分类器

3.1 模糊相关理论

非平稳信号的时频分析工具有多种，比如Gabor变换、短时Fourier变换、模糊函数、Wigner-Ville分布、Cohen类时频分布等。而模糊函数由于在时延-频移平面进行分析的优越性，已经获得广泛应用[17]。模糊函数的数学表达式如下：

(20)

rx(t,τ)=x(t+τ/2)x(t-τ/2)

(21)

式中：x(t)为信号;rx(t,τ)为信号的自相关函数。

同Cohen类时频分布一样，模糊函数对信号进行分析也存在严重的自项和交叉项的干扰，而且计算量大。自项反映了信号本征特点，干扰项则是一种派生项，它们将会对信号的有效分析、解释和各分量参数的提取都有一定的干扰，从而造成信号的时频特征[18-19]。模糊相关分析法可以有效的避开交叉项的干扰，降低时频分析的计算量，为此，文中采用模糊相关分析法对重构信号进行分析，提取管道信号特征。具体算法如下：

(1) 计算两个信号x(t)和y(t)的模糊函数图像的相关函数。

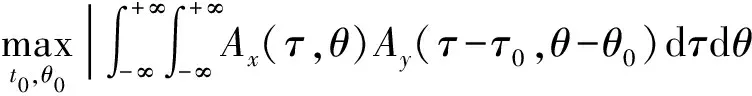
(22)

(2) 利用相关函数计算归一化相关系数，数学表达式如下：

ρxy(τ,θ)=

(23)

(3) 分别取τ=0或者θ=0时的相关系数

ρxy(0,θ)=

(24)

ρxy(τ,0)=

(25)

(4) 计算模糊相关系数

(26)

3.2 分类器基本原理

模糊相关分类器属于一对一分类器。首先对两类信号进行EWT分解，采用自适应降噪法进行处理获得降噪信号，分别计算降噪信号A、B的模糊函数以及测试信号C的模糊函数,利用A类信号的模糊函数和测试信号C的模糊函数，计算相关系数值得到Ⅰ，同理得到信号B和测试信号C的模糊函数的相关系数值Ⅱ，比较Ⅰ和Ⅱ的大小，如果Ⅰ的值大则C为A类，反之则为B类。模糊相关分类器原理如图5所示。

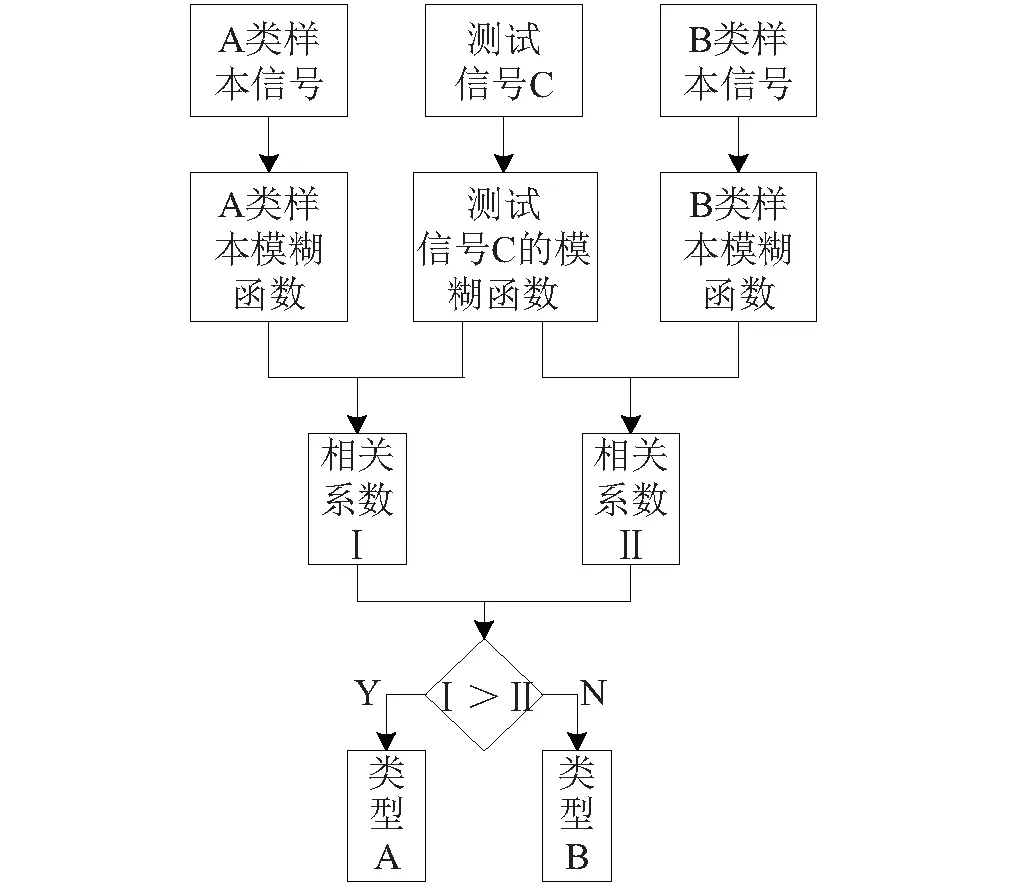
图5 模糊相关分类器原理Fig.5 Classification flowchart

4 实验研究

4.1 实验装置简介

采用传感器、采集卡、承压管道、电脑等搭建实验平台，实验中采用1 mm，2 mm的泄漏孔径进行泄漏实验。在1.0～2.0 MPa实验压力下，通过管内减压的方式以3.1 m/s的流速对管内进行放气，采用NI的USB-6259的数据采集卡以5 Ks/sec的采集速率采集实验数据，实验平台如图6所示。

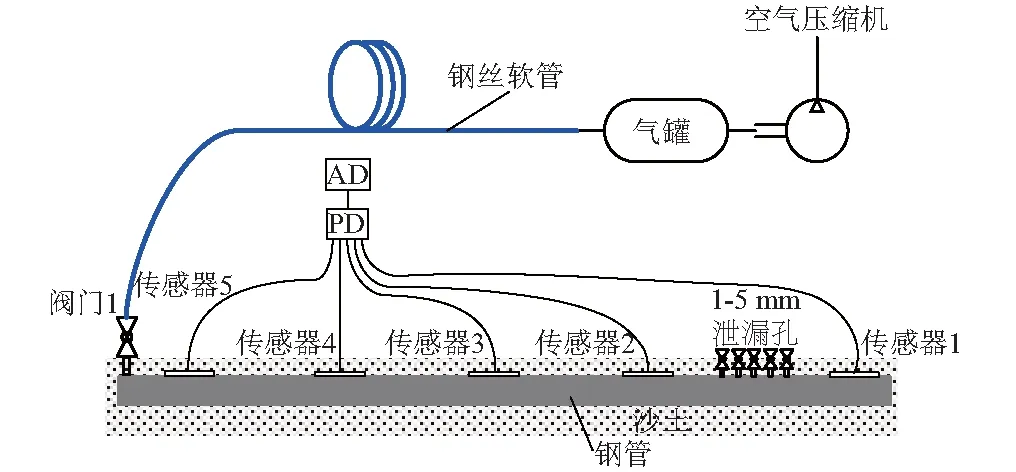
图6 实验系统结构图Fig.6 Schematic of experiment system

利用实验平台，分别采集1 mm泄漏信号、2 mm泄漏信号、正常状态(即无泄漏状态)下产生的信号，如图7所示。

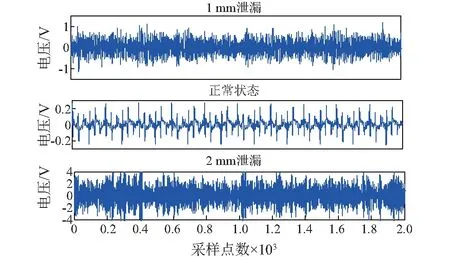
图7 三种状态下采集的信号Fig.7 Signals collected by sensors

以某一传感器在1 mm泄漏状态下采集的信号为例，进行EWT分解，分解结果如图8所示。

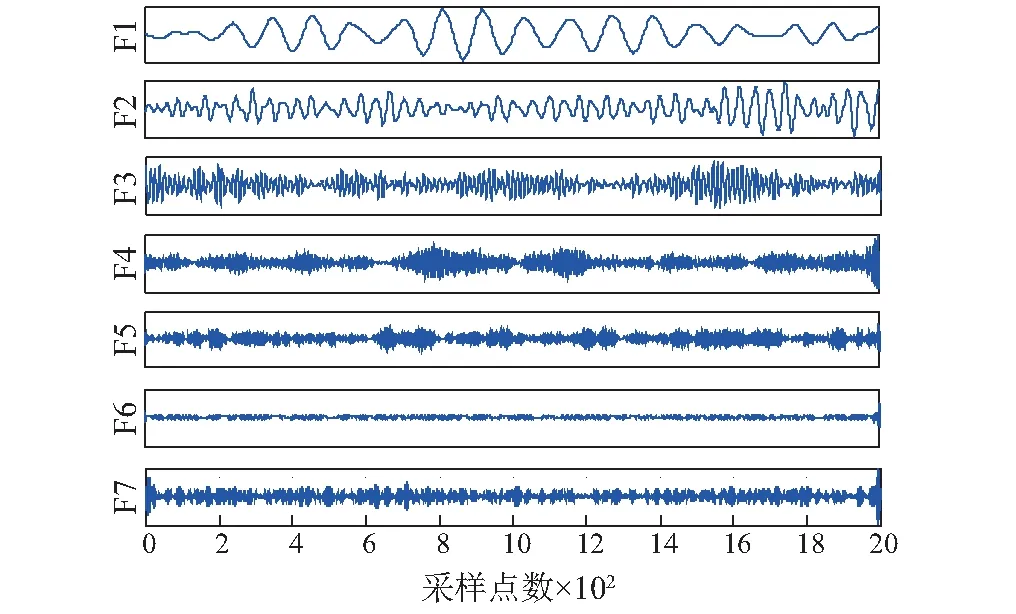
图8 EWT分解结果Fig.8 EWT results of leak signal

对EWT分解后的分量按照上文所述的基于EWT的自适应降噪法进行处理，计算不同分量的峭度因子，并进行排序，结果如图9所示。

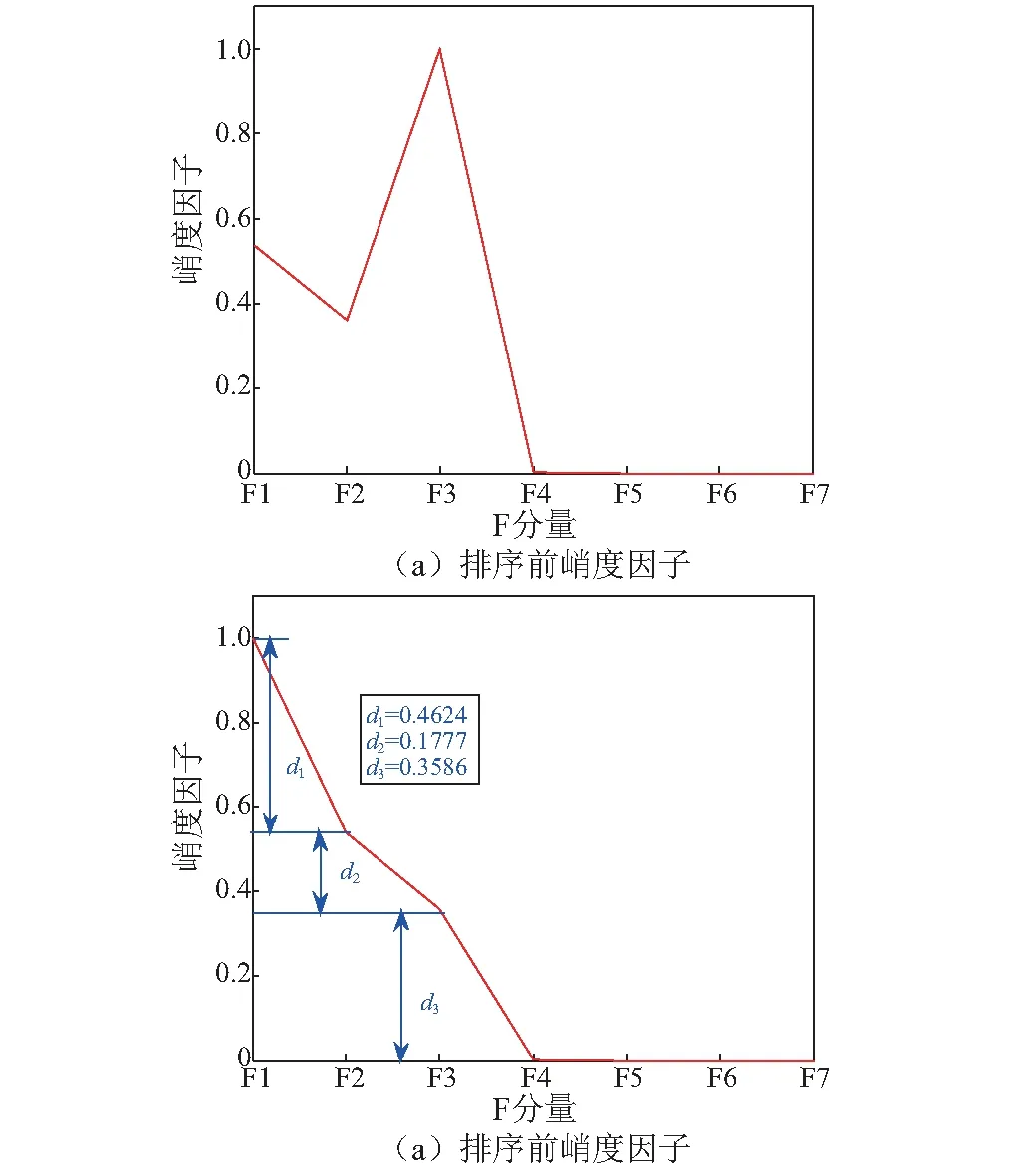
图9 排序前后峭度因子Fig.9 Kurtosis factors before sorting and after sorting

由图9可得，计算不同分量的峭度因子，那么相邻两个分量的峭度因子之差最大值位于F3和F1之间，为此选择前三个分量F1、F2、F3作为有效特征分量，后面的分量为噪声分量，对前三个分量进行重构，形成重构信号。计算重构信号的模糊函数，结果如图10所示。

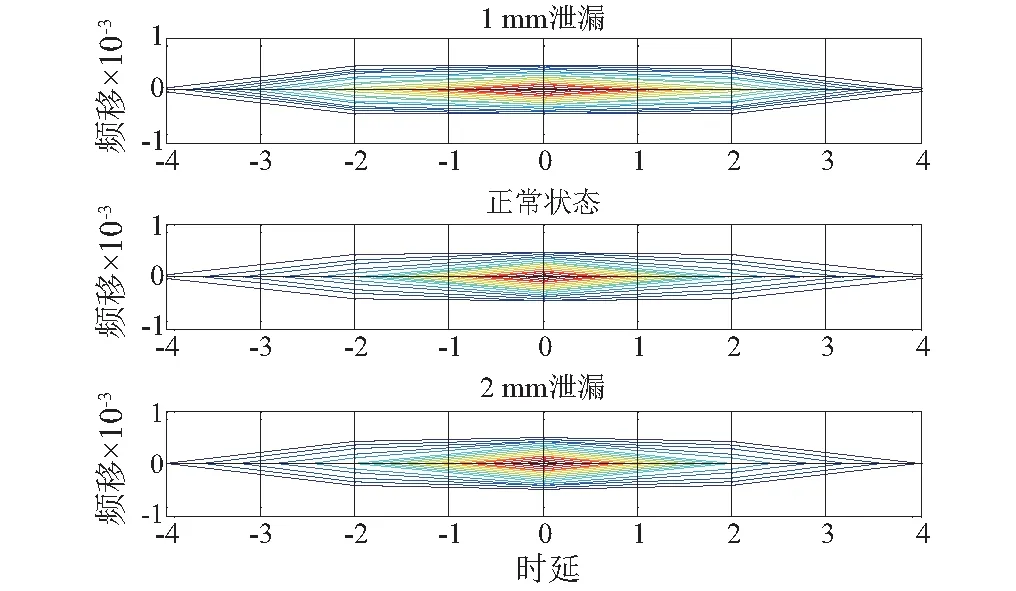
图10 降噪信号的模糊函数图Fig.10 Ambiguity function images of de-noise

观察图10，三种信号的模糊函数在时延和频移方面区别不明显，不能对其进行有效的识别，为此结合相关系数法提出模糊相关分类器，提取三种信号特征，实现管道微小泄漏检测。

为了对比，分别计算基于EWT和基于EMD降噪后信号的模糊相关系数的均值与标准差，结果如表2和表3所示。

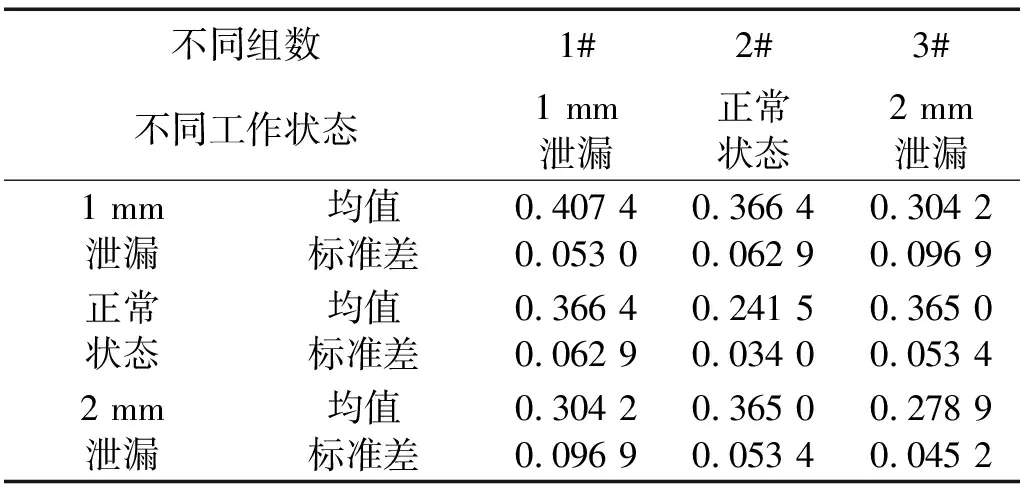
表2 基于EMD相关系数的均值与标准差

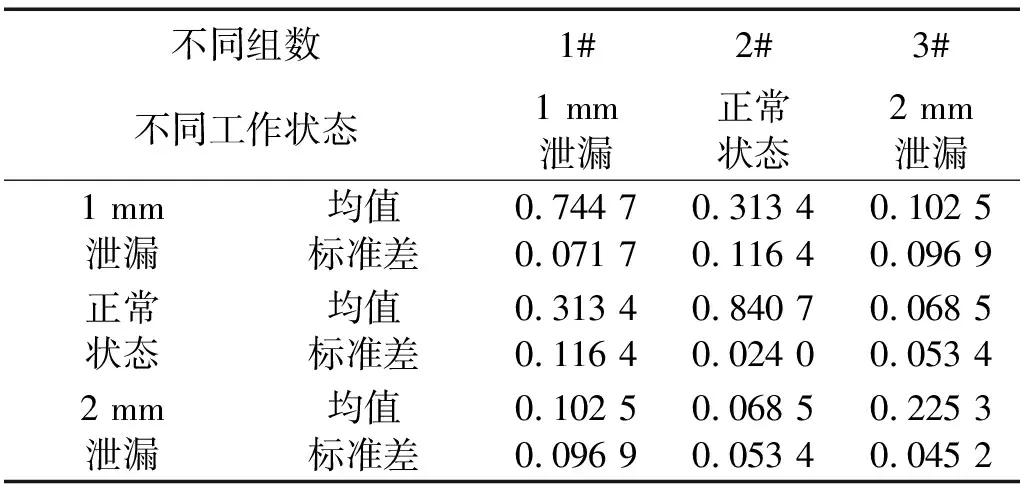
表3 基于EWT的相关系数的均值与标准差

观察表2，由于EMD分解不彻底，无法获取正确的分量，不能去除噪声干扰，因此分解后三种信号在模糊域的相关系数均值区分不明显，无法识别管道不同工作状态。基于EWT降噪法对采集的信号进行处理，提取出固有模态分量，能够正确的分离出噪声分量，因此，表3的三种信号在模糊域的相关系数均值可清晰地区分出不同的类别。为了更直观的对比，根据表2和表3中的均值和标准差，分别作出不同组的相关系数正态分布曲线，结果如图11和12所示。

对比图11和图12，正态分布曲线可以直观的表示三种信号在模糊域的相关程度和识别度。基于EMD降噪法在模糊域的相关系数的正态分布曲线区别不明显，基于EWT降噪后的信号可以将其三种状态区别开来，且模糊域相关系数的正态分布曲线区分较明显。

为了对比，分别采用模糊相关分类器、SVM分类器、BP分类器进行训练与测试。SVM采用线性核函数以二分类的形式进行分类，文中共用三个SVM进行训练与测试；BP神经网络设置3层拓扑结构，采用线性函数训练1 000次，目标误差设定为0.001，它的输出编码为3种模式，分别为[100]、[01 0]、[001]。文中训练数据为20组，测试数据为10组，测试分类结果如图13所示。

观察图13可得，采用三种分类器对三种信号进行训练与测试，能够对三种信号实现分类。其中SVM和模糊相关分类器在小样本情况下就能够实现良好的分类，BP分类器在小样本情况下分类效果差，随着测试样本增多，BP分类器最终实现完全分类。取多组实验数据，分别计算三种分类器的测试精度，结果如图14所示。

图11 基于EMD的相关系数正态分布曲线Fig.11 Normal distribution of correlation coefficient of EMD

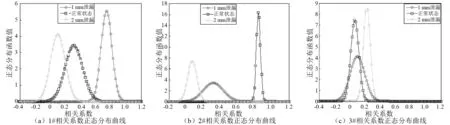
图12 基于EWT的相关系数正态分布曲线Fig.12 Normal distribution of correlation coefficient of EWT

图13 不同分类器的测试分类图Fig.13 The classification result of three methods

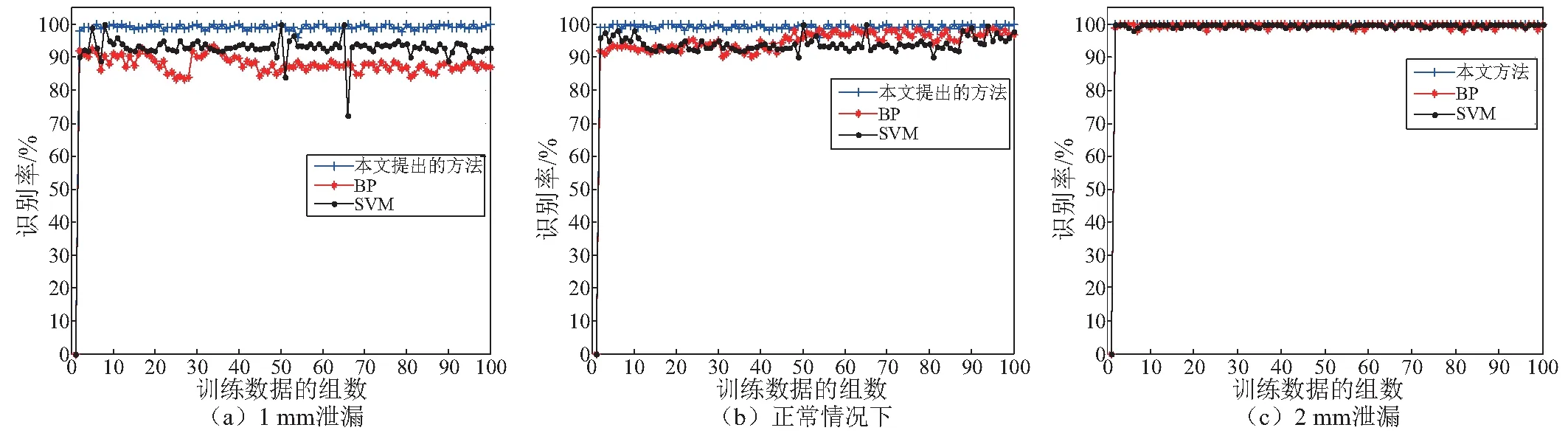
图14 三种分类器的识别率Fig.14 The classification accuracy of the three method

由图14可得，对多组数据进行训练与测试，由于SVM属于统计学习理论，神经网络也属于数据驱动机器学习模型，二者的模式分类效果对于样本数量的依赖性较强，因此在少量样本数据的情况下，SVM及BP的识别率较低，模糊相关分类器的识别率较高；随着样本数据的增加，SVM及BP识别率逐渐提高，最终和模糊相关分类器识别率一样，实现了对天然气管道微小泄漏检测。

取多组不同位置处的数据进行泄漏检测，每组距离为5 m, 分为10组，总距离为50 m，结果如图15所示。对图15分析，本文提出的方法在40 m内特征频率不发生改变，能够对管道微小泄漏进行检测，随着距离的增加，识别率逐渐降低。

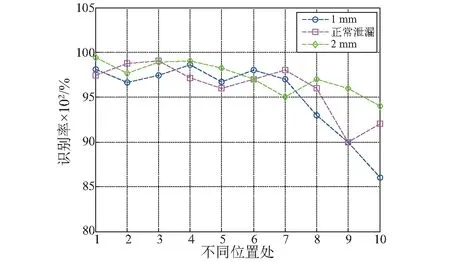
图15 不同位置处的识别率Fig.15 The accuracy of different location

5 结 论

天然气管道发生微小泄漏时，由于管道周边环境复杂，采集的泄漏信号非常微弱，且常常混有大量环境噪声，导致泄漏信号特征不明显，为此，本文提出基于EWT及模糊相关分类器的微小泄漏检测法，并得出了以下结论：

(1) 针对传感器采集的强噪声微弱信号，本文提出基于EWT的自适应降噪法能够自适应的去除噪声干扰，提取声发射信号主要特征。

(2) 针对非平稳振动信号，本文提出模糊相关分类器不仅避免交叉项的干扰，而且降低计算量，实验结果表明该分类器能够检测管道微小泄漏,且检测率较SVM及BP高。