干扰阻塞算法衰减区间分析及改善方法研究

王麟煜， 郑恩明， 陈新华， 黄海宁

(1. 中国科学院声学研究所, 北京 100190; 2. 中国科学院大学，北京 100190)

在复杂多变的水声环境中，均匀线列阵接收数据中真实的目标信号往往被强干扰所掩盖，使得目标检测与跟踪非常困难。研究如何抑制强干扰，提高对弱目标的检测能力显得尤为重要，尤其是当存在主瓣干扰时。

为了抵消主瓣干扰，许多方法被提出。如自适应极化滤波方法(adaptive polarization filter method)[1]，基于大孔径辅助天线方法(large aperture auxiliary array method)[2]，阻塞矩阵(blocking matrix)方法[3-5]，特征投影矩阵(eigen-projection matrix)方法[6-8]等。在这些方法中还存在一些待改善的方面，如Yang等所述自适应极化滤波方法对不同极化宽带干扰效果不好，且自适应加权计算复杂度大；Dai等所述大孔径辅助天线方法需要布防空间较大、不便于工程实现；Yu和李荣峰等所述阻塞矩阵方法会对接收阵造成一定自由度损失，降低部分区间检测性能；Alexander、Yang和Lu等所述特征投影矩阵方法需要精确的主瓣干扰方位，对抗相干干扰性能差、鲁棒性差，且需要进行特征分解、计算复杂度大。因运算量小，常被工程应用的阻塞矩阵方法最早由Yu提出，被用于克服波束形成时协方差矩阵估计信号混入问题，其后被用于抗干扰方面的研究[9-11]。苏保伟等[12]首先将阻塞矩阵方法应用于主瓣抗干扰；王纯等[13]提出基于Householder变换构建干扰阻塞矩阵的方法；陈辉等[14]将阻塞矩阵法应用于强干扰背景下弱信号的估计中，提高了弱信号的检测概率和估计精度；罗丁利等[15]针对分布式目标信号将阻塞矩阵方法进行改进，使之在目标信号方向形成比较宽的“凹口”，提高算法的稳健性；苏成晓等[16]在此基础上实现了弱信号二维DOA估计；虽然高阳等针对主瓣干扰情况，采用输出信干噪比(Signal to Interference and Noise Ratio，SINR)增益、抗干扰输出波束图等对抗干扰性能进行衡量，分析了阻塞矩阵抗干扰方法存在的问题及适用性，但并未给出详细的衰减区间分析、相应影响因子和改善方法。

从文献资料可以看出，在干扰阻塞算法(Jamming Jam Method，JJM)应用中，鲜有文献对干扰阻塞算法衰减区间进行详细分析，阐明影响因子，并提出相应改善方法，以便减小干扰阻塞算法衰减区间，提高该算法在相应方位区间的检测性能。该文为了详细分析干扰阻塞算法衰减区间，推导了干扰阻塞算法实现原理，干扰阻塞算法后线阵输出总能量、信号、噪声、信噪比相关函数，以及干扰阻塞前后总能量、信号、噪声、信噪比变化函数。通过变化函数证实了干扰阻塞算法对线阵输出总能量、信号、噪声的衰减趋势一致，论述了影响衰减区间相关因子，并提出了相应改善方法。改善方法通过修正因子减小了干扰阻塞算法衰减区间，提高了该算法在该方位区间的检测性能，可对原衰减区间的弱目标实现检测。并通过数值仿真和海试数据处理结果验证了本文所述改善方法在抵消主瓣内强干扰时，降低了背景能量差异，减小了衰减区间，对相邻干扰2°的弱目标实现了有效检测，提高了抗干扰性能和检测性能。

1 干扰阻塞算法

(1)

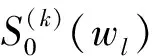
则各阵元接收数据矩阵X(k)(wl)表示形式为

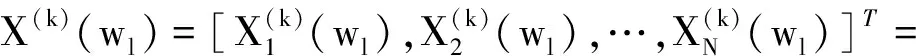
(2)

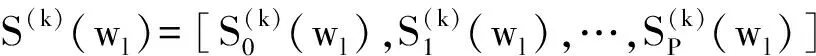
干扰阻塞算法就是利用已知强干扰入射角θ0作为先验知识对A(wl)进行阻塞，进而将干扰阻塞掉，阻塞矩阵W(wl,θ0)构造如下所示

(3)

利用阻塞矩阵对阵列流形矩阵A(wl)进行阻塞处理，可得

W(wl,θ0)A(wl)=
[a′(wl,θ0),a′(wl,θ1),…,a′(wl,θP)]

(4)

式中：a′(wl,θ0)=[0,0,…,0]为干扰阻塞后(N-1)×1维阵列流形矢量，a′(wl,θP)=[1,ejwld cos θp/c,…,ejwl(N-2)d cos θp/c]T·(1-ejwld(cos θp-cos θ0)/c)为第p个目标信号经干扰阻塞后(N-1)×1维阵列流形矢量。

由a′(wl,θp)可知，阻塞矩阵在阻塞强干扰的同时，目标信号也会受到影响。阻塞矩阵阻塞强干扰后，线阵接收目标信号等效为

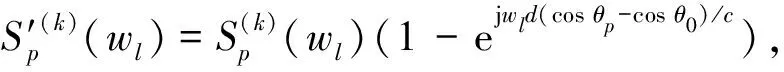
(5)

2 干扰阻塞算法衰减区间分析

2.1 理论分析

干扰阻塞前，由K组采样数据得到的协方差矩阵R(wl)可以表示为

(6)

式中： [·]H表示矩阵共扼转置。

其空间谱可表示为

(7)

式中：Wbf(wl,θ)=[1,ejwld cos θ/c,…,ejwl(N-1)d cos θ/c]T为干扰阻塞前波束形成加权因子;θ表示目标相对于水平线阵的方位角，一般取值为θ∈[0,Θ],Θ=180。

干扰阻塞后，由K组采样数据得到的协方差矩阵R′(wl)可以表示为

(8)

式中：X′(k)(wl)，N′(k)(wl)，a″(wl,θp)如下所示

a″(wl,θp)=[1,ejwld cos θp/c,…,ejwl(N-2)d cos θp/c]T

JJM所得空间谱可表示为

(9)

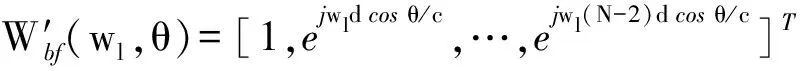
以第p个目标为例，对干扰阻塞后输出数据进行分析说明，干扰阻塞后线阵接收数据变为

(10)

令线阵各阵元接收数据中，信号与背景噪声、背景噪声与背景噪声之间互不相关。由式(10)可知，干扰阻塞后线阵接收数据协方差矩阵变为

(11)

式中：γ=(2-ejwld(cos θp-cos θ0)/c-e-jwld(cos θp-cos θ0)/c)。

(12)

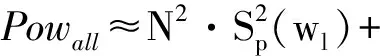
(13)

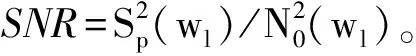
式(13)给出了干扰阻塞算法会对线阵输出总能量、信号、噪声、信噪比造成不同程度的衰减函数；由该函数可知，干扰阻塞算法对线阵输出总能量、信号、噪声造成的变化主要与式中γ有关，其变化趋势一致，在信号频率和入射角θp一定时，影响衰减区间相关因子为输入信噪比SNR、阵元数N、阵元间距d、强干扰方位角θ0。

2.2 数值仿真分析

为了进一步验证干扰阻塞算法对线阵输出总能量、信号、噪声、信噪比造成的衰减受相关因子影响程度，进行如下仿真分析。仿真分析中信号频率为f1=80 Hz， 则角频率wl=2πfl， 声速为c=1 500 m/s， 信号波长为λ=c/f1。接下分析输入信噪比SNR、阵元数N、阵元间距d、强干扰方位角θ0对线阵输出总能量、信号、噪声、信噪比造成衰减的影响。由于干扰阻塞算法对线阵输出总能量、信号、噪声造成的变化趋势一致，以下仿真结果只给出了输出总能量和信噪比。

(1) 阵元间距d=λ/2， 输入信噪比为SNR=1， 阵元数为N=64。不同强干扰方位角θ0情况下，线阵输出总能量、信噪比衰减区间仿真结果，见图1，2。

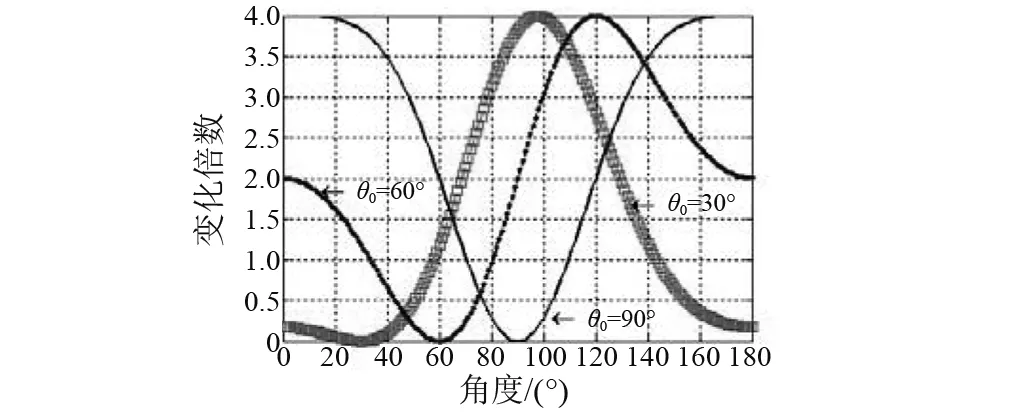
图1 线阵输出总能量衰减区间(干扰方位变化)Fig.1 The attenuation interval of linear array output total energy (interference bearing change)

(2) 强干扰方位角为θ0=30°，输入信噪比为SNR=1，阵元数为N=64。不同阵元间距d情况下，线阵输出总能量、信噪比衰减区间仿真结果，见图3，4。

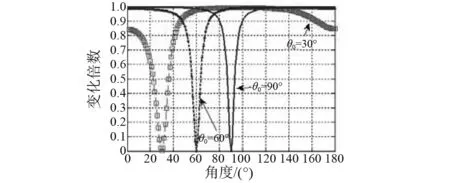
图2 线阵输出信噪比衰减区间(干扰方位变化)Fig.2 The attenuation interval of linear array output SNR (interference bearing change)

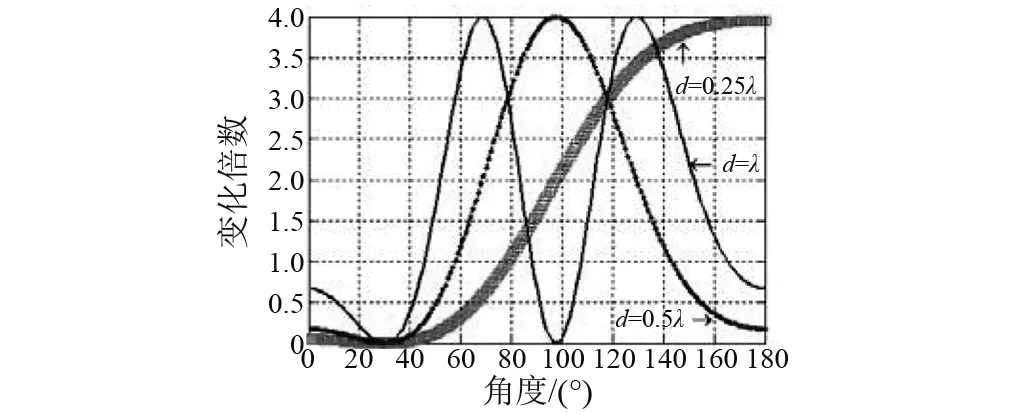
图3 线阵输出总能量衰减区间(阵间距变化)Fig.3 The attenuation interval of linear array output total energy(array space change)

图4 线阵输出信噪比衰减区间(阵间距变化)Fig.4 The attenuation interval of linear array output SNR (array space change)

(3) 强干扰方位角为θ0=30°， 阵元间距d=λ/2， 阵元数为N=64。不同输入信噪比SNR情况下，线阵输出总能量、信噪比衰减区间仿真结果，见图5，6。

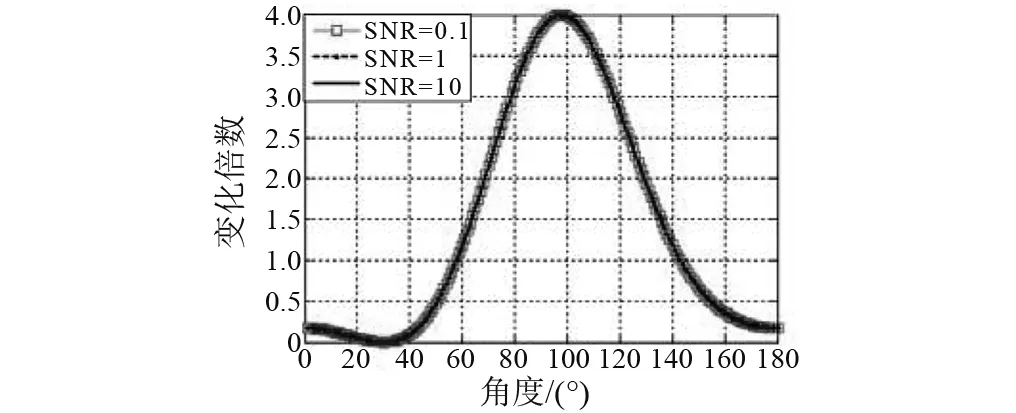
图5 线阵输出总能量衰减区间(信噪比变化)Fig.5 The attenuation interval of linear array output total energy(input SNR change)

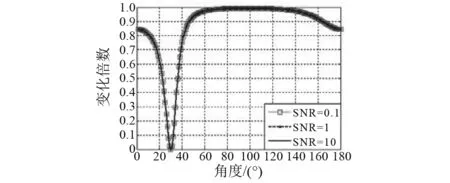
图6 线阵输出信噪比衰减区间(信噪比变化)Fig.6 The attenuation interval of linear array output SNR (input SNR change)

(4) 强干扰方位角为θ0=30°， 阵元间距d=λ/2， 输入信噪比SNR=1。不同阵元数N情况下，线阵输出总能量、信噪比衰减区间仿真结果，见图7，8。

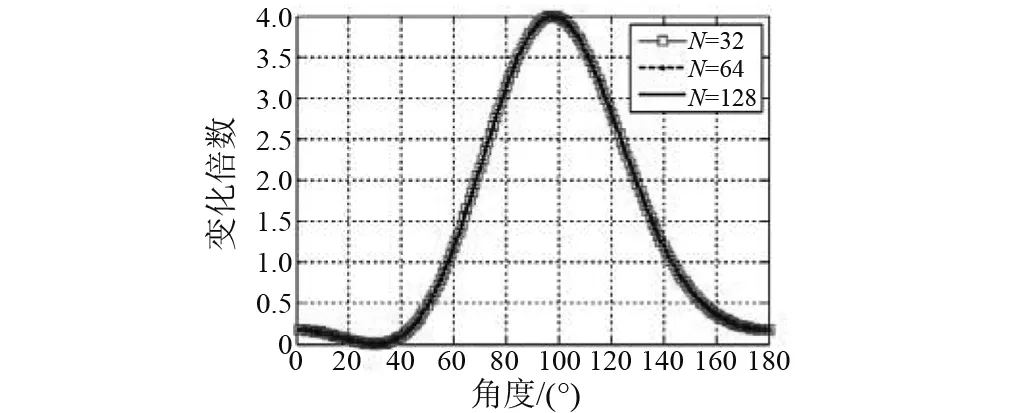
图7 线阵输出总能量衰减区间(阵元数变化)Fig.7 The attenuation interval of linear array output total energy(the number of array element change)

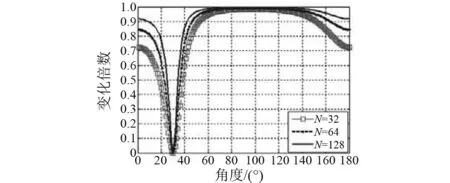
图8 线阵输出信噪比衰减区间(阵元数变化)Fig.8 The attenuation interval of linear array output SNR (the number of array element change)

由图1～8可知，JJM会对线阵输出总能量造成不同程度的衰减，输出总能量在一部分方位区间被增强，而在另一部分方位区间被降低；而输出信噪比在某些方位区间被降低。由于输出总能量的较大差异，将影响衰减区间弱目标检测，降低该区间弱目标检测性能。在信号频率一定时，干扰阻塞算法对线阵造成的衰减受阵元数N影响较小，受阵元间距d和强干扰方位角θ0影响较大，不受输入信噪比SNR。 所以，影响衰减区间的主要因子为阵元间距d和强干扰方位角θ0。

3 干扰阻塞算法改善方法

3.1 理论分析

由式(11)可知，干扰阻塞前后线阵接收数据的协方差矩阵在信号和噪声项都有一定差别，而干扰阻塞前后的波束形成过程中所用加权因子形式一致，因此，除干扰方位之外，干扰阻塞前后线阵形成在其他方位的处理结果存在一定差别。

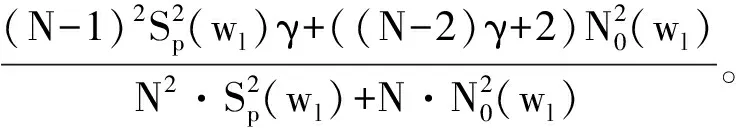
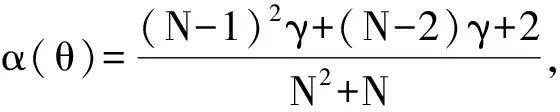
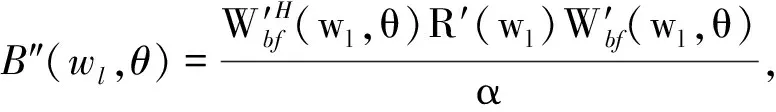
(14)

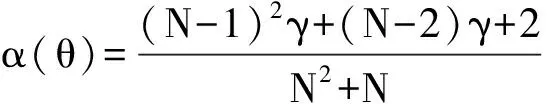
由式(14)可知，经修正因子修正后，在θ∉[θ0-Δθ1,θ0+Δθ2]处，干扰阻塞前后线阵输出总能量、信号、噪声、信噪比比值为1，即改善方法可以有效降低干扰阻塞算法对线阵输出总能量、信号、噪声、信噪比的影响。

由于修正因子与干扰方位相关θ0，在干扰方位未知时，可通过判断(1-ejwld(cos θ-cos θ0)/c)=0事先求得干扰方位θ0，然后再采用式(14)实现对干扰阻塞方法的修正。

3.2 数值仿真分析

为了进一步验证改善方法可以有效降低干扰阻塞算法对线阵的影响，进行如下数值仿真分析。

令强干扰、目标1与目标2信号频率均为fc=80 Hz，强干扰与目标1方位角分别为θ0=70°和θ1=72°，目标2方位角随时间变化，背景噪声为带宽fn=40～120 Hz的白噪声，声速为c=1 500 m/s，阵元间距d=λ/2，λ=c/fc。 目标1与目标2功率比值为0 dB，目标1与强干扰功率比值为-30 dB，目标1与背景噪声功率比值为-25 dB。图9～12由不同方法在fc频率单元处所得。

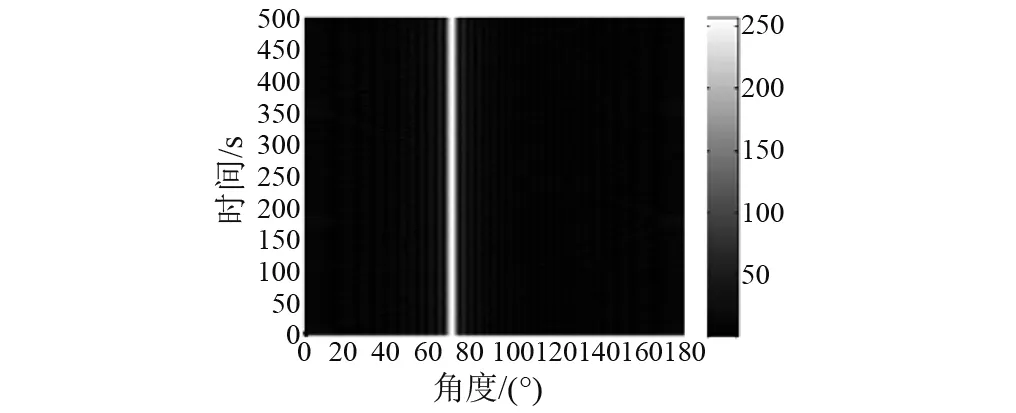
图9 方位历程图(干扰抵消前)Fig.9 The Bearing/Time record map (before interference suppression)

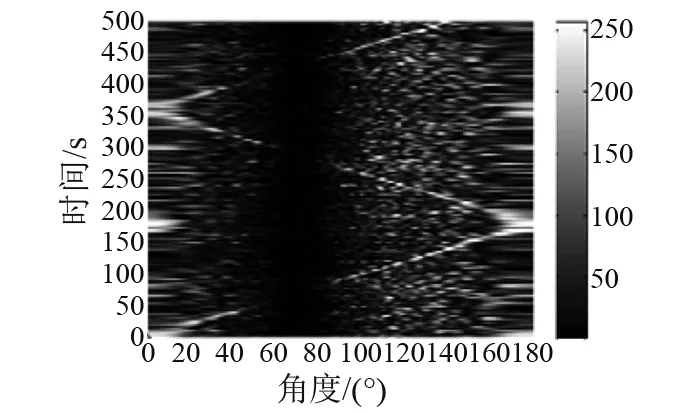
图10 方位历程图(JJM抵消干扰)Fig.10 The Bearing/Time record map (interference suppression of JJM)

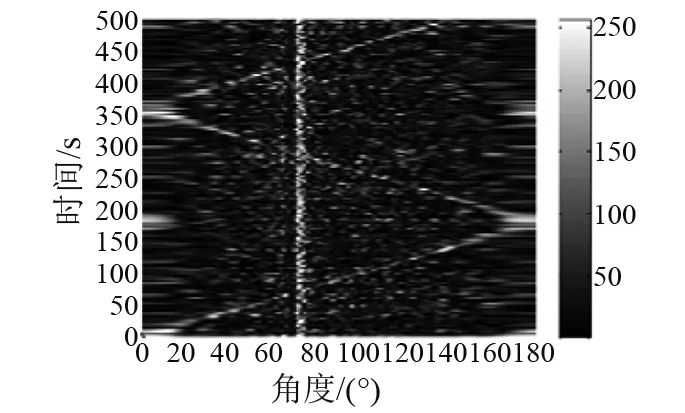
图11 方位历程图(本文方法抵消干扰)Fig.11 The Bearing/Time record map (interference suppression of this method)

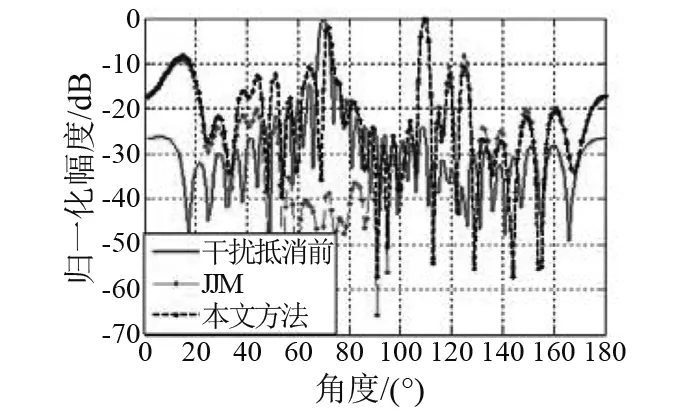
图12 波束图Fig.12 The beam map

由图9～12可知，在抵消θ0=70°处强干扰时，由于JJM会对线阵输出总能量造成不同程度的衰减，强干扰方位相邻目标不能被有效检测；而本文方法采用了修正因子对JJM进行了改善，降低了JJM会对线阵输出总能量造成的影响，在抵消θ0=70°处强干扰时，强干扰方位相邻目标被很好地检测。数值仿真结果验证了本文方法通过修正因子减小JJM衰减区间，在抵消强干扰时，可对相邻弱目标实现有效检测。

3.3 海试数据处理

本次试验数据为2012年在南海进行目标检测试验所得。试验采用32元水平线阵接收信号，阵间隔为8 m，水平线阵尾端方向设为180°。

数据处理实例1：处理实测数据长度为220 s，所用采样率为fs=5 kHz。滤波器频带为f=40～80 Hz，图13～16由不同方法所得。

图13 方位历程图(干扰抵消前)Fig.13 The Bearing/Time record map (before interference suppression)

图14 方位历程图(JJM抵消干扰)Fig.14 The Bearing/Time record map (interference suppression of JJM)

图15 方位历程图(本文方法抵消干扰)Fig.15 The Bearing/Time record map (interference suppression of this method)

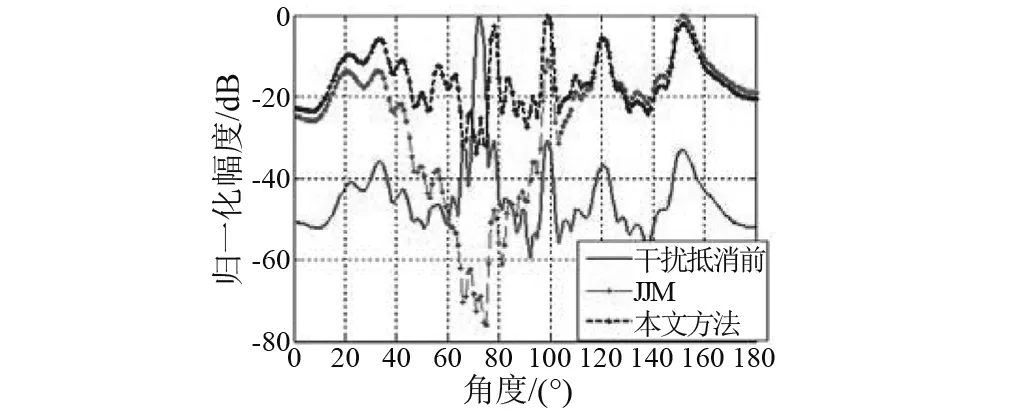
图16 波束图Fig.16 The beam map

由图13～16可知，在抵消θ0=73°附近强干扰时，由于JJM会对线阵输出总能量造成不同程度的衰减，强干扰方位相邻目标不能被有效检测；而本文方法采用了修正因子对JJM进行了改善，降低了JJM会对线阵输出总能量造成的影响，在抵消θ0=73°附近强干扰时，强干扰方位相邻目标被很好地检测。试验数据1处理结果验证了本文方法通过修正因子减小JJM衰减区间，在抵消强干扰时，可对相邻弱目标实现有效检测。

数据处理实例2：处理实测数据长度为120 s，所用采样率为fs=5 kHz。 滤波器频带为f=60～100 Hz，图17～20由不同方法所得。

图17 方位历程图(干扰抵消前)Fig.17 The Bearing/Time record map (before interference suppression)

图18 方位历程图(JJM抵消干扰)Fig.18 The Bearing/Time record map (interference suppression of JJM)

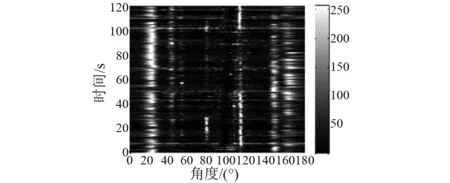
图19 方位历程图(本文方法抵消干扰)Fig.19 The Bearing/Time record map (interference suppression of this method)

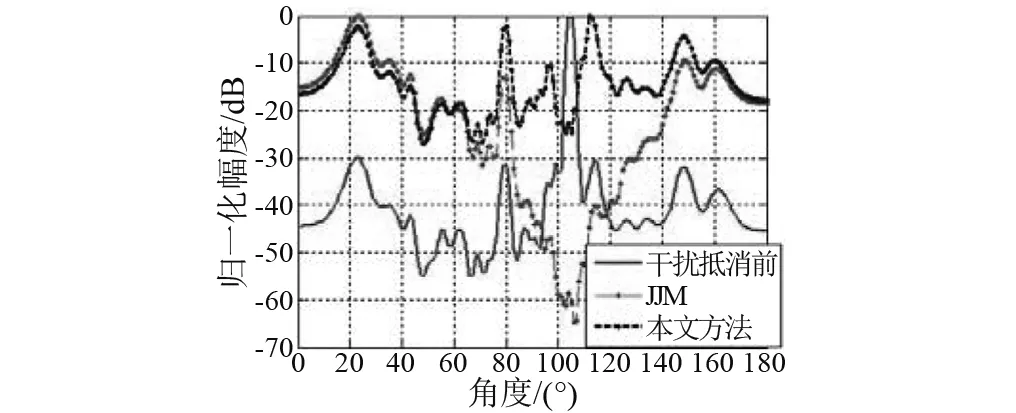
图20 波束图Fig.20 The beam map

由图17～20可知，在抵消强干扰时，由于JJM会对线阵输出总能量造成不同程度的衰减，强干扰方位相邻目标不能被有效检测；而本文方法采用了修正因子对JJM进行了改善，降低了JJM会对线阵输出总能量造成的影响，在抵消强干扰时， 113°处弱目标被很好地检测。试验数据2处理结果验证了本文方法通过修正因子减小JJM衰减区间，在抵消强干扰时，可对相邻弱目标实现有效检测。

4 结 论

本文详细推导了干扰阻塞算法实现原理，干扰阻塞算法后线阵输出总能量、信号、噪声、信噪比相关函数，以及干扰阻塞前后总能量、信号、噪声、信噪比变化函数。通过变化函数证实了干扰阻塞算法对线阵输出总能量、信号、噪声的衰减趋势一致，论述了影响衰减区间相关因子。数值仿真进一步验证了变化函数中相关因子对线阵输出数据造成的不同程度影响。根据理论和数值仿真分析结果，提出了改善干扰阻塞算法相应方法，改善方法通过修正因子减小了干扰阻塞算法对线阵输出总能量、信号、噪声、信噪比造成的衰减区间，在抵消主瓣内强干扰时，原衰减区间弱目标可被有效检测，提高了干扰阻塞算法抗干扰性能。

数值仿真和海试数据处理结果进一步验证了相比干扰阻塞算法，本文所述改善方法在抵消主瓣内强干扰时，通过修正因子有效降低了背景能量差异，降低了干扰阻塞算法对衰减方位区间内目标检测性能影响，对相邻干扰2°的弱目标实现了有效检测(本文仿真条件下，如果抵消角度接近法线方向，相邻更近处目标也可实现有效检测)，提高了干扰阻塞算法抗干扰性能和检测性能，为进一步提高了干扰阻塞算法的性能提供一种可行方案。