塑料排水板处理地基固结计算及其工程应用分析

黄 朝 煊

(浙江省水利水电勘测设计院，杭州 310002)

0 引 言

真空预压法就是在需要加固的软基中插入竖向排水通道(如砂井、袋装砂井或塑料排水板等)，然后在地面铺设一层砂垫层，再在其上覆盖一层不透气的土工膜。在膜下抽真空形成负压(相对大气压而言)，负压沿竖向排水通道向下传递，在负压作用下，孔隙水逐渐渗流到竖向排水通道中而达到土体排水固结、强度增长的效果。真空预压法作为新一代软基加固方法，以其工期短、施工安全、无污染环境、费用低等优点而广泛应用于港口、码头、机场、工业与民用建筑等工程建设，但对排水结构的排水效率和固结度之间关系的研究仍有待深入。

在20世纪40年代，Barron[1]最先对砂井地基固结问题进行建模分析，研究圆形砂井地基的固结过程，但未对带状排水板处理地基进行研究；W Kjellman K[2]最新对真空预压加固软土地基进行了试验研究，但未给出真空预压固结计算理论；国内1957年由哈尔滨军事工程学院最早进行真空预压试验，后来众多学者对真空预压机理进行了深入研究，如岑仰润[3]对真空预压进行了深入的试验和理论总结，但其计算理论引用砂井地基固结理论；黄朝煊等[4-6]对带状排水板处理地基固结理论进行了深入研究，认为带状排水板与圆形在形状上差异显著，不可避免带来计算误差，并给出了堆载预压下的扁矩形带状排水板地基固结新理论，但未对真空预压荷载作用作相应说明；黄朝煊等[7]对砂井地基真空预压处理及漏气影响进行了研究，但未对带状排水体计算做深入研究；INDRARATNA B等[8]采用有限元理论对真空预压进行了数值计算模拟，但需要借助大型有限元计算软件，不便于一般工程设计人员应用。

因此，基于目前真空预压法加固软土地基采用扁矩形带状排水板，且该型排水结构的排水效率与固结度关系研究仍采用砂井地基等效计算的不足，本文将扁矩形带状排水板等效为形状接近的扁椭圆柱体，基于椭圆柱坐标系理论对真空联合堆载预压加固软土地基进行了探讨分析，并通过浙江省某围垦工程水闸软基础真空预压预加固处理案例，及相关监测资料对比验证总结分析，为相关工程设计提供参数，以便于排水板椭圆柱固结计算理论在工程应用中大量推广。

1 真空联合堆载预压处理地基固结度计算

目前带状排水板的固结理论是近似采用砂井等效法，即将带状排水板采用等效直径的柱状砂井等效，由于两者形状差异太显著，不可避免会带来计算差；相比于圆柱体等效方法，将塑料排水板等效为椭圆体显然更合适。 在工程实际中，塑料排水板会按一定的间距(S)和深度(L)打设。塑料排水板在平面内的布置方式主要有正三角形(梅花形)和正方形两种，如图1所示，单个竖井的排水范围通常会等效为圆柱体，在三角形布置时，等效后圆柱体排水范围直径de=1.05S；正方形布置时，de=1.128S。

图1 塑料排水板的不同布置形式简图

根据椭圆柱坐标系理论(见图2)，椭圆的面积A=πa2·chρ·shρ，采用单个竖井的排水范围与同焦椭圆面积等效原则，可确定排水范围相应参数，对于梅花形布置时：

(1)

式中：a为椭圆柱等效排水体的半焦距，m，可取a=0.52b；b为排水板的宽度，m；S为排水板中心间距，m。

如：排水板中心间距S=0.8 m，排水板宽b=100 mm，厚度δ=4 mm，则单竖井排水等效范围参数ρe=2.782 2(长轴2achρe=0.843 3 m，短轴2ashρe=0.836 8 m)。

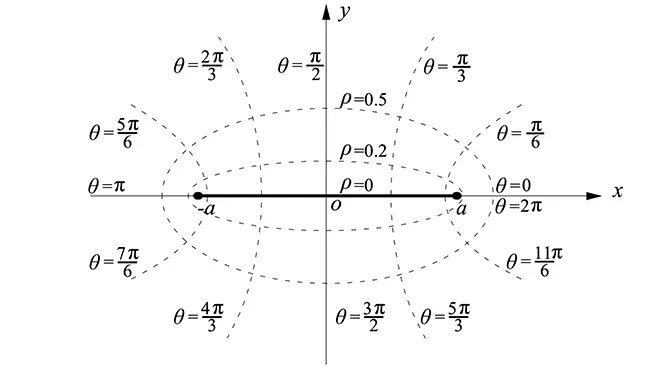
图2 ρ、θ坐标下的椭圆坐标系

同样，排水板矩形布置时：

(2)

如：排水板中心间距S=0.8 m，排水板宽b=100 mm，厚度δ=4 mm，则单竖井排水影响范围参数ρe=2.854 2(长轴2achρe=0.905 7 m，短轴2ashρe=0.899 8 m)。

排水板的椭圆柱等效模型见图3，参数L为排水体计算长度，ρw分别为椭圆柱排水体的径长坐标；ρs为同焦椭圆柱涂抹区径长坐标；ρe为排水体的同焦椭圆影响区径长坐标；u为土中超孔压；kw为竖井渗透系数；kh为土的径向渗透系数；ks为涂抹层的渗透系数。

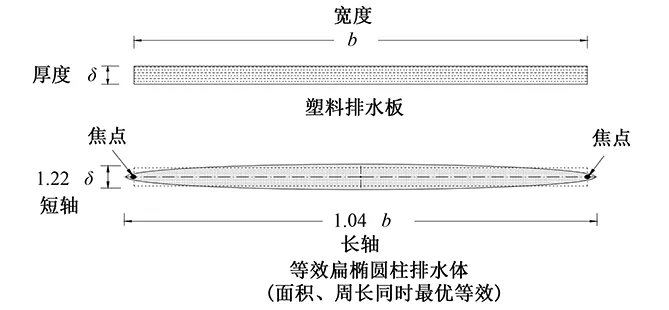
图3 塑料排水板的椭圆柱等效模型

根据同焦椭圆坐标系中径向坐标ρ与椭圆扁度(短、长轴比)的关系可知，ρ→∞，则椭圆扁度→1，越接近于圆，椭圆长轴2achρ→2ashρ→d=2r，即椭圆的两焦点在逐渐靠拢以至于趋向于一点时，椭圆便逐渐退化为标准圆，两焦点便退化为圆心。

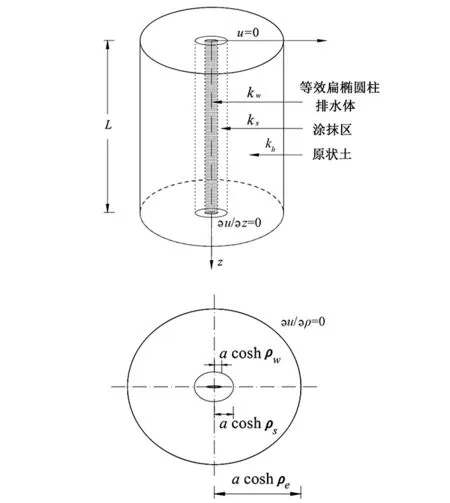
图4 椭圆柱固结理论计算简图

基于等应变假设，黄朝煊等[4-6]依据土力学理论及严密的数学理论推导，在考虑带状排水板井阻(kw)、涂抹(ρs)影响下，可得带状塑料排水板处理地基固结解析解，其中总平均固结度计算式为：

(3)

其中参数：

(4)

(5)

其中参数Fh计算如下：

(6)

(7)

(8)

cosh2ρs)sinh2ρe-8C1sinh2ρs]

(9)

Fws_2={4C2[exp(2ρs)-exp(2ρw)]-

4C3[exp(-2ρs)-exp(-2ρw)]-(ρs-ρw)}

(10)

(2ρesinh2ρe-cosh2ρe)sinh2ρe-8E1sinh2ρe]

(11)

Fse_2={4E2[exp(2ρe)-exp(2ρs)-

4E3[exp(-2ρe)-exp(-2ρs)]-(ρe-ρs)}

(12)

其中待定参数分别为：

(13)

(14)

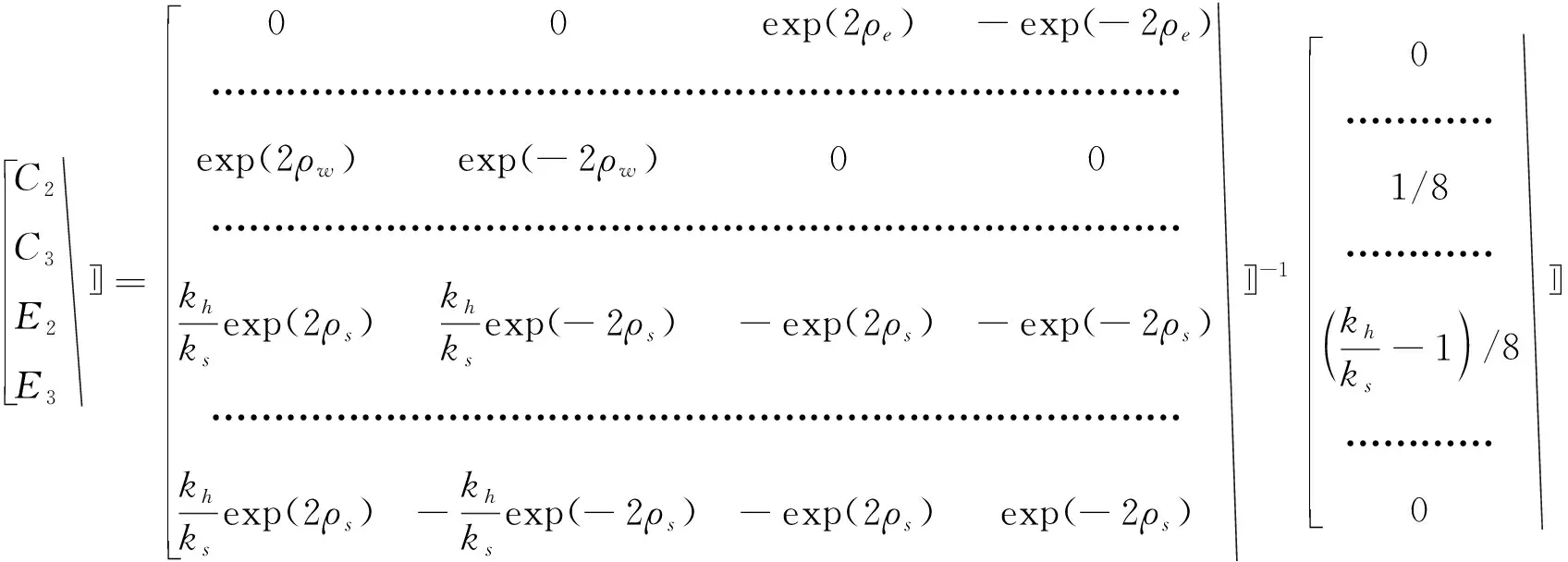
(15)

以上公式相应参数可根据基本参数ρw、ρs、ρe、a、kh、ks求出。

其中计算流程示意图见图5，过程如下。

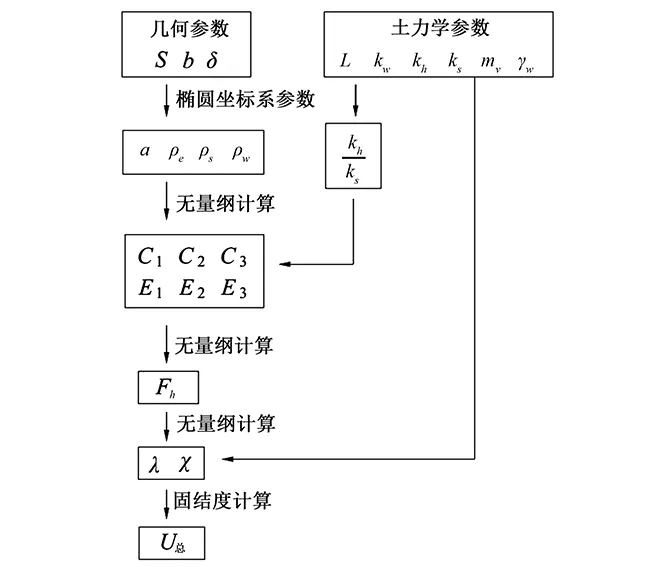
图5 椭圆柱固结理论计算简图

根据带状塑料排水板宽度b=100 mm，厚度δ=4 mm以及等效模型简图3可知，等效后的椭圆柱排水体长轴为1.04b=104 mm，短轴为1.22δ=4.88 mm，根据椭圆性质的半焦距参数：

进而可得：

根据面积等效原则， 模型计算区参数：

即等效单井模型的长轴为acoshρe=1.002 8 m，等效单井模型的短轴为asinhρe=0.997 3 m，其长轴和短轴近似相等，即非常接近于直径为1.0 m的圆形，不考虑涂抹影响，即ρs=ρw。

根据本文公式(2)、(3)计算参数C1、E1、C2、E2、C3以及E3，然后根据公式(28)可知Fws、Fse，进而计算参数Fh，可利用公式(2)无量纲时间因子计算总平均固结度曲线。

通过真空联合堆载预压，地基土中有效应力增加，地基土抗剪强度的增长，其中真空预压过程中有效应力增长原理见示意图6。

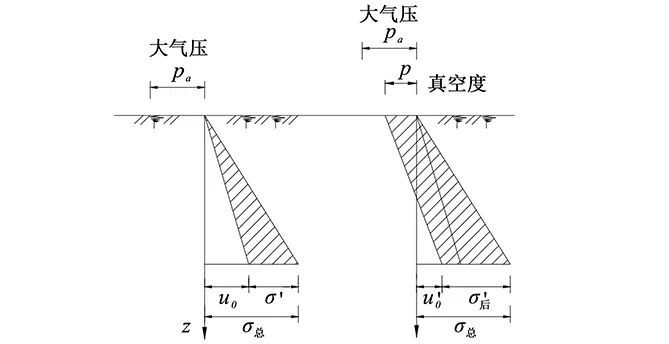
图6 真空预压原理示意图

2 真空联合堆载预压应用案例概况

2.1 项目概况

某工程防洪标准为50年一遇，近期防潮标准为10年一遇，并在20年一遇超标准工况下不发生严重破坏和溃坝，工程等别为Ⅲ等，主要建筑物西河堤及排涝闸均为3级建筑物，水闸围堰设计挡潮标准为非汛期5年一遇。

排涝闸为胸墙式水闸，排涝流量498 m3/s，净宽42 m，7孔×6 m，闸底槛高程-2.0 m，闸基坐落在深厚淤泥软土地基上。

水闸地基土层主要为Ⅲ0层淤泥、Ⅲ1层淤泥夹砂、Ⅲsis层细砂、Ⅲ2层淤泥质黏土、Ⅳ1层淤泥质黏土粉土、Ⅳsis层粉砂和Ⅴ层黏土组成。闸基土层Ⅲ0层淤泥、Ⅲ1层淤泥夹砂、Ⅲ2层淤泥质黏土、Ⅳ1层淤泥质黏土夹粉土均为高含水量、高压缩性、高灵敏度、低强度的软土，工程地质条件差。Ⅳsis层粉砂性质较好，但厚度变化较大且埋深较大；Ⅴ层黏土性质较好，但埋深较深。Ⅳsis层粉砂和Ⅴ层黏土可作为桩基持力层。具体土层物理力学参数见表1。

2.2 真空预压布置

基础处理采用真空预压及真空联合堆载预压，见图7。为了对比传统真空预压处理、真空联合堆载预压处理以及不处理3种方式对地基土的物理力学指标的影响，将原设计地基处理的区域分为A、B、C，3个区块。

表1 真空预压现场实验区地质参数统计表

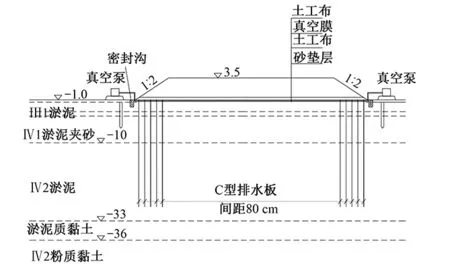
图7 真空预压布置简图

传统真空预压处理范围(A区)：范围尺寸117.8 m×56.8 m，面积6 691.04 m2。不处理区(B区)：长宽各15 m，面积225 m2。真空联合堆载预压处理范围(C区)：面积8 492.2 m2。

真空预压时间4个月，真空预压1个月后左右岸开始联合堆载预压，第一层堆载控制为0.5 m，采用黏土或细粒土人工摊铺，第二、三层堆载控制为1.5 m，采用抛石或山皮土，第一、二层堆荷加载间歇时间为0.5个月，第二、三层堆荷加载间歇时间为1个月。当真空预压恒载满足下列标准后可停泵卸载： ①连续10 d观测的沉降速率小于1 mm/d； ②固结度大于80%。

2.3 监测布置

监测项目包括：真空度监测、表面沉降监测、孔隙水压力监测、分层沉降监测、水平位移监测、水位监测等内容。

孔隙水压力计、分层沉降、水位等膜下监测仪器与插板同步进行埋设，真空表、地表沉降板待铺设密封膜后及时进行安装并获取各监测项目初始值，开始抽真空后，原位监测单位及时进行膜下监测仪器的出膜工作，并按设计频次要求开展日常观测工作，及时反馈监测成果。

3 监测成果分析

3.1 监测成果

抽真空初期，膜下真空度一直维持在较低水平(0～40 kPa)；3月4日、3月10日经施工单位两次密封沟处理后，膜面密封效果有所改善，膜下真空度上升到60 kPa左右；3月21日起停泵开始密封墙施工，膜下真空度降至零，3月25日重新开始抽真空，由于开泵数量少，膜下真空度一直在10 kPa以下；4月4日起开始增加开泵数量，膜下真空度逐步上升，4月8日密封墙施工完成，随着开泵数量的增加，膜下真空压度达到80 kPa左右。膜下真空度变化过程线详见图8。

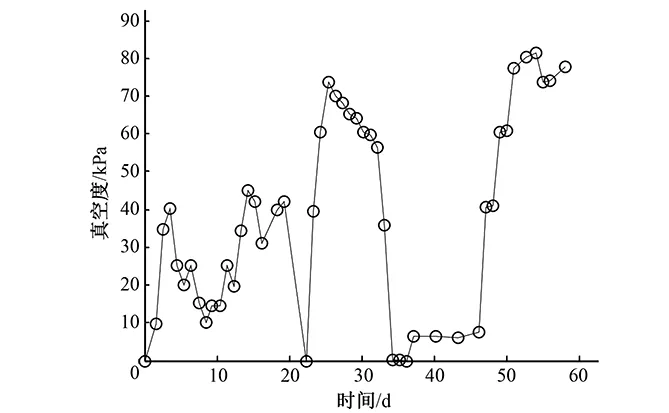
图8 膜下真空度变化过程线

3.2 孔隙水压力

随着膜下真空压力的上升，孔隙水压力均有一定程度的消散，当膜下真空压力下降时，孔隙水压力出现反弹现象，土层孔隙水压力的消散程度与膜下真空度保持了较好的相关性；土层孔隙水压力消散主要集中-15 m高程以上，最大累计消散值在50 kPa左右，且沿深度方向呈现明显递减趋势。处理区孔隙水压力过程线分别见图9。

图9 孔隙水压力值变化过程线

通过对预压加固过程中孔隙水压等相关数据监测分析，认为真空预压过程中存在漏气问题，膜下真空度与原设计值存在较大偏差，通过延长真空预压时间及增加堆载预压厚度以保证深厚淤泥软土的前期预沉降，增加软土地基承载力。

3.3 地表沉降

抽真空初期，由于膜下真空压力较低，地基沉降发展缓慢；密封沟处理后随着膜下真空压力的上升，沉降速率也随之增大，最大沉降速率达15 mm/d；之后受停泵密封墙施工影响，膜下真空压力迅速下降，地表沉降出现反弹现象；随着密封墙施工完成，膜下真空压力增加，沉降速率随之增大。处理区地表沉降变化过程线见图10。

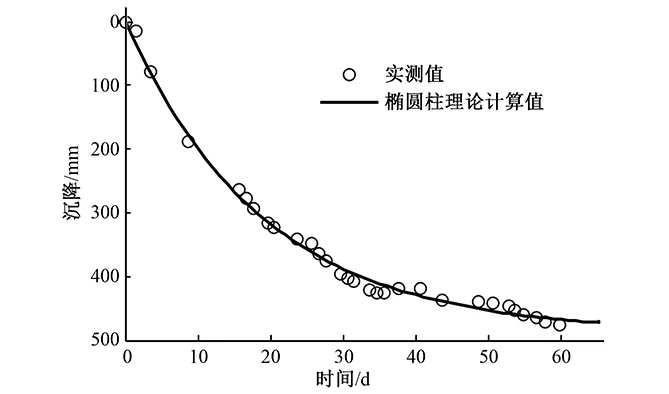
图10 处理区地表沉降变化过程线

由于真空预压过程中真空度波动较大，本次沉降计算中，真空度荷载取平均值40 kPa进行计算，堆载荷载按P=4.5 m×1.75 t/m3=7.88 t考虑，其中沉降计算采用以下公式：

s(t)=U(t)s

(16)

其中地基总平均固结度U(t)按本文椭圆柱固结理论公式(2)计算，地基沉降s按以下公式计算：

(17)

通过真空预压及增加堆载预压厚度，以减小深厚淤泥软土孔隙率，增加软土地基承载力，控制后续工程建筑物之间差异沉降及不均匀沉降，保证建筑物整体安全性。其中实测沉降及本文理论计算值见图10，通过沉降计算并与实测沉降值对比分析，认为带状排水板的椭圆柱固结理论与实际沉降监测值基本吻合，为该理论的推广应用提供理论基础。

4 结 语

针对目前带状塑料排水板处理地基固结计算近似采用砂井地基固结理论的不足，对真空联合堆载预压处理下的带状排水板处理地基固结进行研究，并通过我院实际工程案例验证对比分析，本文主要结论如下：

(1)将带状排水板等效为形状接近的扁椭圆柱体，考虑排水板井阻、涂抹影响的新固结理论，基于椭圆柱坐标系理论给出了总平均固结度的解析计算式，并给出其计算原理及流程示意图，便于工程师实际工程应用计算。

(2)依托于某围垦工程深厚淤泥软基础真空联合堆载预压相关资料，通过对预压加固过程中孔隙水压、沉降等相关数据监测分析，认为真空预压过程中存在漏气问题，膜下真空度与原设计值存在较大偏差，通过延长真空预压时间及增加堆载预压厚度以保证深厚淤泥软土的前期预沉降，以减小深厚淤泥软土孔隙率，增加软土地基承载力，控制后续工程建筑物之间差异沉降及不均匀沉降，保证建筑物整体安全性。

(3)通过本文提出的带状排水板处理地基椭圆柱固结理论下的沉降计算对比，并与实测沉降值对比验证分析，认为带状排水板的椭圆柱固结理论与实际沉降监测值基本吻合，为该理论的推广应用提供理论基础。