洪水预报实时校正技术比较及应用研究

周 梦，陈 华，郭富强，许崇育

(武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072)

0 引 言

洪水预报是根据前期和现时的水文、气象等信息，揭示和预测洪水的发生及其变化过程的应用科学技术。进行洪水预报的水文模型主要是采用观测到的历史水文资料和数据，确定模型参数的合理值，然后对未来的水文数据进行预测从而进行洪水预报。当系统的参数随时间变化时，普通的参数估计将无法得到确定的最优值，实时校正就是追踪系统参数的变动过程寻找合适的参数来进行系统模拟[1]。

在实时洪水预报系统中，每次预报做出之前，实时校正模型根据当时的实测信息(新息)对预报模型的参数、状态变量、输入向量或预报值进行某种校正，使其更符合客观实际。现在模型洪水预报实时校正涉及两方面的研究内容：一是建立洪水实时预报校正模型；二是采用有效的实时校正技术[2]。实时洪水预报校正技术有典型的水文模型流量预报实时校正算法[1]，其在多站点的大流域和流量陡涨陡落的流域局限性比较大；误差自回归校正算法[3]关键在于其回归系数的确定，确定之后无需改动模型，计算量较少，但是其使用效果跟预报的残差与前期残差序列的一致性;衰减记忆最小二乘算法[4]其重点在于实时洪水遗忘因子的确定，但是洪水过程随机性较大，可以针对不同洪水选取合适的遗忘因子；卡尔曼滤波算法[5]可以有效滤掉实测及预报噪声，关键在于模型噪声和量测噪声方差矩阵的确定；基于贝叶斯理论的自适应实时校正模型[6]其能够充分利用先验信息以及实测信息得到预报的后验分布，关键在于误差分布的估计以及模型参数的确定。这些方法都能根据实测信息及时更新预报数据，来提高预报精度。

现有研究中对于某一流域不同方法的适用性比较较少，并且少有比较各种方法对于不同洪水评价指标的表现的文章，所以本文在建溪流域进行实例研究，在新安江水文模型模拟的基础上比较了误差自回归实时校正模型、卡尔曼滤波算法以及基于贝叶斯理论的实时校正方法的适用性。

1 研究区域与数据

建溪流域位于福建省的北部，流域面积14 787 km2，流域平均降水量1 600～2 600 mm，是福建省锋面雨高值区。如图1所示，建溪七里街水文站以上有崇阳溪、南浦溪和松溪三大支流。本文主要研究七里街及其上游的流域，涉及的水文站点有麻沙站，崇安站，管潭站，松溪站，建阳站，水吉站，新厂站以及七里街站。

本研究用到的数据为2005-2014年的小时观测数据，取2005-2013年为率定期，2014年作为检验期，时间步长取1 h，对场次洪水进行计算。校正主要是对检验期新安江模型的模拟数据进行校正，选取的场次洪水共有10场。

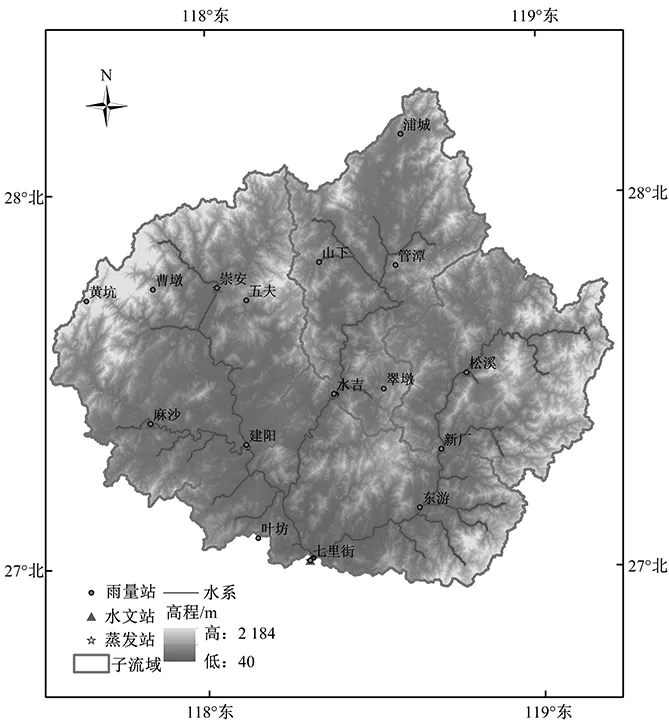
图1 建溪流域图Fig.1 Jianxi river basin

2 模型及方法介绍

2.1 新安江模型

新安江模型是由赵人俊教授领导的研究组在20世纪70年代提出的模拟径流模型，在80年代由二水源模型发展成为了三水源模型，适用于湿润地区与半湿润地区。三水源新安江模型蒸散发计算采用三层蒸散发模型；产流计算采用蓄满产流模型；用自由水蓄水库结构将总径流划分为地表径流、壤中流和地下径流三种；流域汇流计算采用线性水库；河道汇流采用马斯京根分段连续演算或滞后演算法[7]。本次率定模型所用的优化算法是SCE-UA算法(Shuffled Complex Evolution),SCE-UA算法是一种全局优化算法，适合新安江模型这类高维参数的全局优化[8-10]。

新安江模型主要有15个参数需要率定[11],分段马斯京根法对于不同的河段，参数k和x需要各自率定。现根据历史蒸发、降雨以及径流资料，可以用全局优化方法率定参数，得到最优的模拟模型。

2.2 AR算法

洪水预报误差序列具有拖尾的特性，且为白噪声，故洪水预报误差序列为平稳时间序列，可采用时间序列AR模型进行实时校正[12]。其主要是对模型残差序列采用残差自回归估计式：

et+L=c1et+c2et-1+…+cpet-p+1+ξt+L

(1)

那么预报结果的校正式为：

(2)

其中：

et=Q(t)-QC(t)

2.3 Bayesian算法

(3)

假定天然径流过程满足自回归滑动模型，先验分布用自回归滑动平均模型进行模拟；假定实测径流和预报径流服从线性关系，似然函数使用AR模型进行模拟。

2.4 卡尔曼滤波算法

卡尔曼滤波理论的基本思想即采用信号与噪声的状态空间模型，利用前一时刻的估计和观测值来更新对状态变量的估计，求现时刻的估计值[13]。其采用一个状态方程和一个量测方程来完整的描述线性动态过程，前者描述系统状态向量随时间的变化规律，后者采用函数关系反映量测向量与系统状态向量之间的依赖关系[14]。其递推公式既可以得到滤波估计值，又可以得到误差的方差阵，即可以完成自身的误差分析[15]。其公式可以表示为：

状态方程：

Xt+1=FtXt+BtUt+wt

(4)

量测方程：

Yt=HtXt+vt

(5)

式中：Xt为状态向量；Yt为测量向量；Ut为系统的输入；wt、vt分别为状态噪声和测量噪声，且wt、vt为独立一致的正态随机变量；Bt、Ht为传输矩阵；Ft为系统从t到t+1时刻的n×n维状态转移矩阵[6]。

2.5 建溪流域洪水预报模型

本研究主要用到新安江模型及3种实时校正模型，如图2所示，先根据历史资料建立建溪流域新安江模型，确定汇流参数，以及区间的新安江模型参数。再用新安江模型进行检验期的流量模拟以及预报，预报时假设预报时刻以后流域降雨为零。预报值会分别经过3种校正方法进行校正，校正前后的值会通过分段马斯京根法汇流到七里街，区间用新安江模型进行预报，最后可以汇总得到七里街的流量预报。再次用相应的方法进行校正。

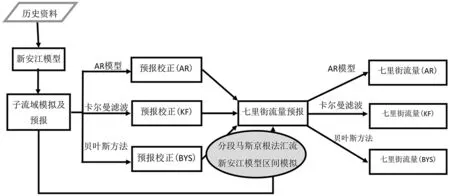
图2 建溪流域洪水预报模型结构图Fig.2 Technology roadmap

3 结果与讨论

3.1 模型模拟结果

根据子流域区间降雨蒸发数据以及上游流量汇流，新安江模型可以对子流域流量数据进行模拟，然后采用分段马斯京根法进行七里街汇流计算，区间继续采用新安江模型进行模拟，得到的预报结果如表1所示。

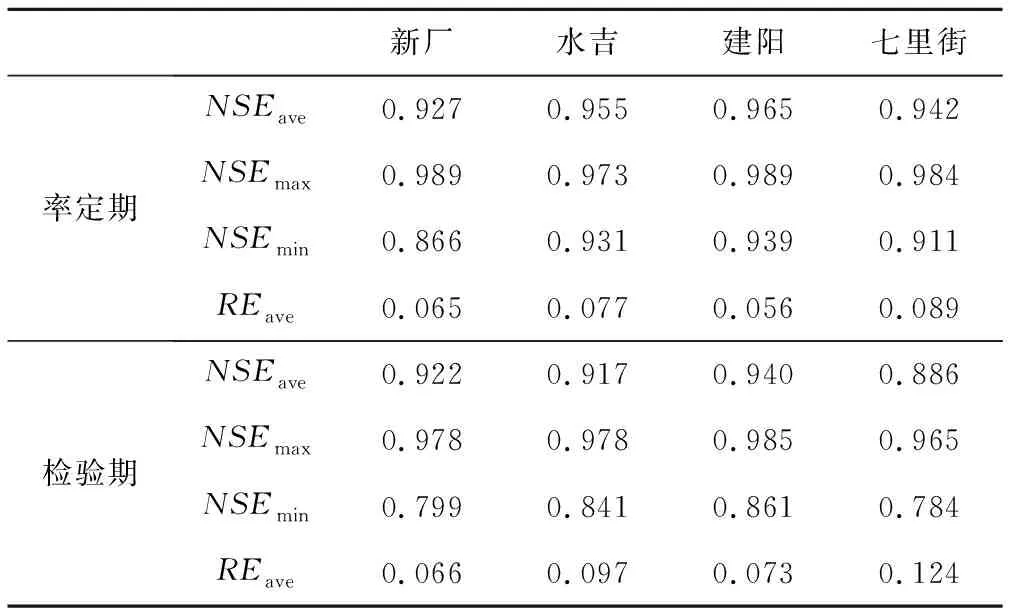
表1 率定期及检验期新安江模型模拟结果Tab.1 Simulated results for calibration and validation period

表1列出了新安江模型模拟的结果，率定期为2005-2013年，检验期为14年。可以看到，率定期的洪水平均纳西效率系数都达到了0.9以上，子流域的模拟情况普遍比整个大流域的模拟情况要好。检验期最小的纳西效率系数都不到0.9，子流域的平均纳西效率系数还是保持在0.9以上。对于各场洪水模拟的结果来看，80%的子流域洪水模拟纳西效率系数都高于0.9，对于个别洪水，有的子流域降雨很少，洪峰不明显，所以模拟效果不够好，但是对整个流域的误差影响较小。

3.2 各校正方法校正结果比较分析

子流域的预测及校正完成后，用校正后的预测数据，采用分段马斯京根法进行七里街汇流计算，区间继续采用新安江模型进行模拟预报，得到的预报结果如表2所示。

由表2可以看到，3种校正方法都相较于新安江模型模拟值明显提高了精度，纳西效率系数能增加0.15左右，水量平衡误差也大大降低。随着预见期的增加，预报精度降低，就研究洪水的平均水平来说，对于前几个小时的预见期，贝叶斯方法的纳西效率系数和水量平衡误差这两个指数都优于其余两种方法。在预见期增加后，AR模型校正的水量相对误差比较小，在预见期大于9之后，卡尔曼滤波的纳西效率系数较高，而贝叶斯方法的相对误差较小。综合来看，贝叶斯方法在纳西效率系数和水量误差方面在各场洪水的总体水平上上表现较好。

为了具体分析各种方法不同预见期的表现，现在对于每场洪水的纳西效率系数进行统计，找出每场洪水最高和最低的纳西效率系数如表3所示。

各种方法在不同预见期时纳西效率系数最高和最低的频率如图3所示，由柱状图的分布情况可以明显发现，贝叶斯方法对短预见期表现最好，模拟出纳西效率系数比另外两种方法好的频率很高，但是随着预见期的增加，贝叶斯方法的优势呈降低趋势，在预见期超过6 h时已呈劣势。相反地，卡尔曼滤波校正方法对短预见期的校正效果不如贝叶斯方法和AR方法，但是在预见期扩大时，开始显现出明显的优势。这说明卡尔曼滤波校正技术比贝叶斯方法更适合长预见期的洪水。而AR方法很稳定，频数分布比较均匀，对各预见期表现没有明显变化趋势。综合比较，在预见期较短时，可以选择贝叶斯方法，而预见期变长之后，可以选择卡尔曼滤波方法。

表2 不同预见期新安江模型与各校正方法的平均纳西效率系数以及平均水量误差Tab.2 Average NSE and RE of data forecasted by Xinanjiang model and three correction methods in different prediction period

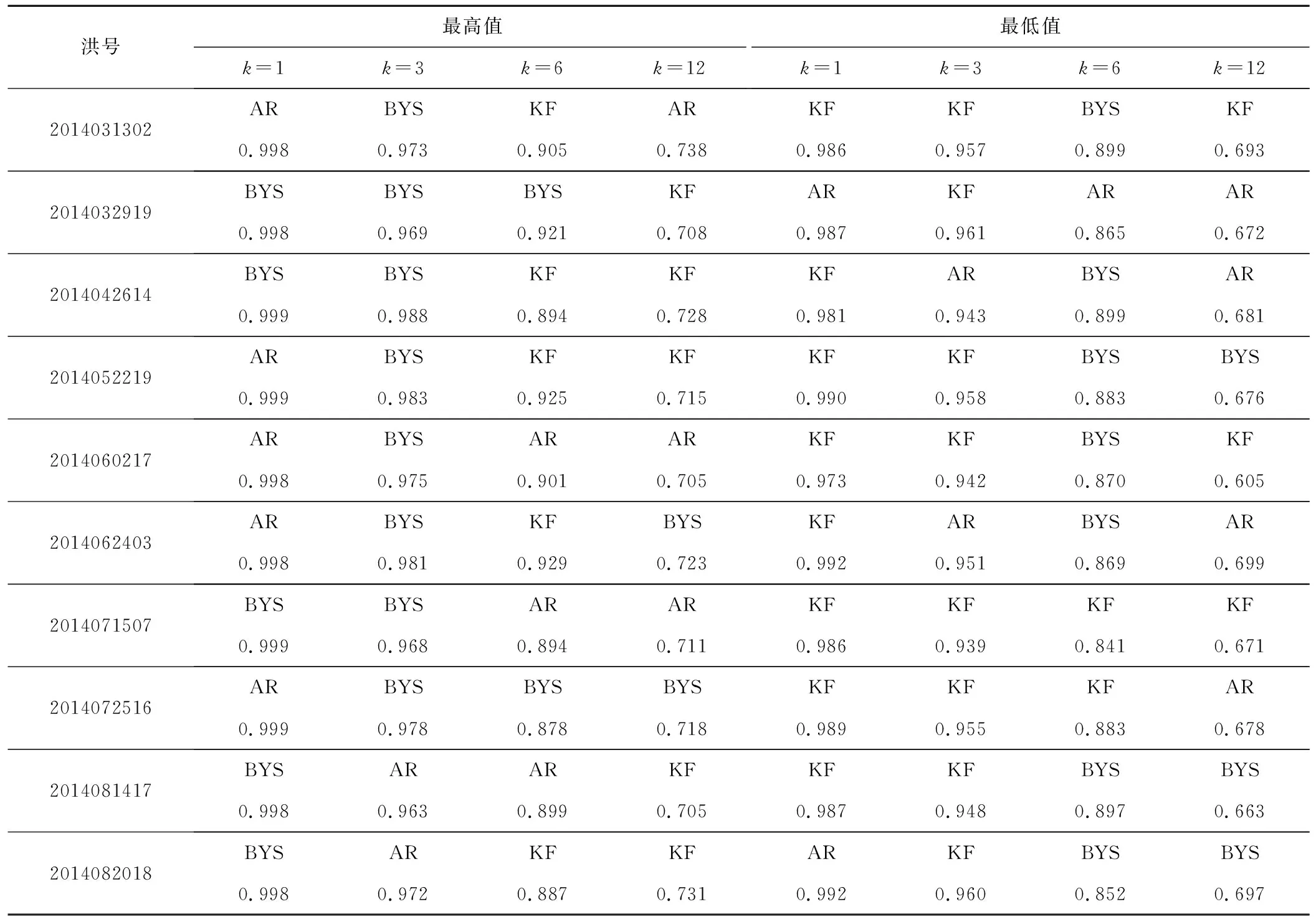
表3 各校正方法校正之后的纳西效率系数比较Tab.3 Comparison of NSE after correction of three correction methods

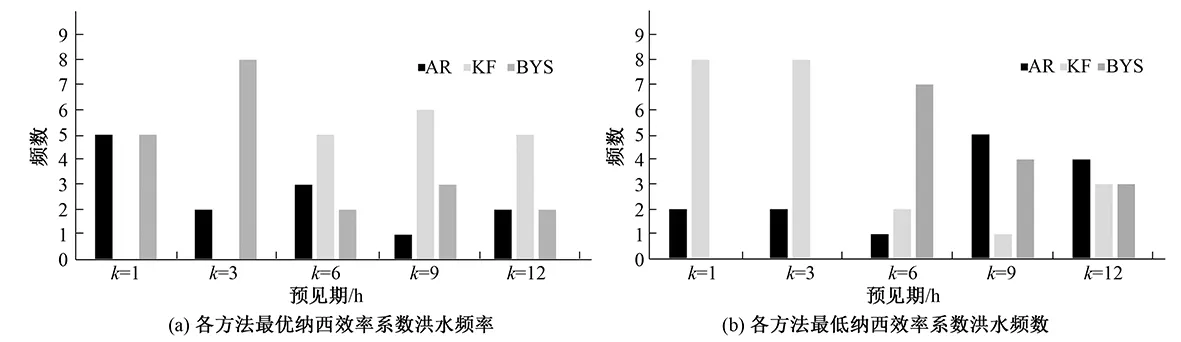
图3 各种方法校正之后得到最高和最低纳西效率系数的频率比较Fig.3 Frequency comparison of the highest and lowest NSE after correction of three methods

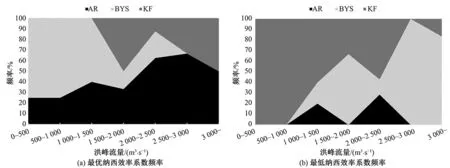
图4 各方法校正之后对应不同洪峰流量的最高最低纳西效率系数频率比较Fig.4 Frequency comparison of maximum and minimum NSE corresponding to different peak flow after different methods correction[16] Maximum NSE Minimum NSE

除了考虑不同校正方法跟预见期的关系，还考虑到不同方法的校正效果可能跟洪峰流量有一定的关系。子流域以及整个流域各场洪水的洪峰流量以及6个预见期时各种校正方法校正效果如图4所示，可见AR方法在6个预见期时表现较好，得到最优纳西效率系数的次数比较稳定，贝叶斯方法对于低流量洪水表现较好，卡尔曼滤波比较适合高流量的洪水。

洪水预报中，对洪水洪峰的预测也十分重要，现在对不同预见期预测的洪水的洪峰误差进行统计，得出比较图如图5所示。

图5 各校正方法不同各预见期的洪峰误差比较Fig.5 Comparison of flood peak errors at different forecast periods with different correction methods

由图5可以看到，各个校正方法在前两个预见期预报精度都比较高，洪峰误差都在±3%以内，在预见期延长时，误差都在扩大，三种方法校正效果从图中可以看到，卡尔曼滤波和贝叶斯方法，较于AR模型洪峰误差较小，并且从分布区间和中位数来看，卡尔曼滤波表现更好，洪峰误差较小。

图6以20140725这场洪水为例，展示了不同预见期3种方法预报的结果，可以看到，随着预见期的增加，预报值偏离实测值越来越远。在3个预见期时，3种方法的校正曲线比较接近实测值，但是已经不再光滑，在到12个预见期时，已经偏离较远了，这是因为12个预见期，在用新安江模型预报时，假设没有降雨，12个预见期没有降雨这在雨量方面的误差过大，这个时候的预报精度已经不能很好的保证了，只能做一个大致的参考。

4 结 语

建溪流域雨量丰沛，气候湿润，新安江模型本身就可以较好地模拟洪水过程。AR模型，卡尔曼滤波以及贝叶斯方法3种校正方法都能明显提高流量模拟的精度，对于不同的评判指标，3种校正方法校正效果有所不同。对于水量相对误差，贝叶斯方法校正后效果最好，AR模型与卡尔曼滤波方法校正结果不相上下。AR模型和卡尔曼滤波方法校正之后的洪水过程纳西效率系数保持很高，卡尔曼滤波方法对于长预见期或者流量较大的洪水表现得比较好，可以得到更好的纳西效率系数，而贝叶斯方法对于流量较小的洪水表现得更好，AR模型对于各个量级的洪水都能有比较好的表现。综上，3种方法都能在实际应用中达到较为理想的效果，根据不同的预报需求，可以选择相应的方法进行校正。

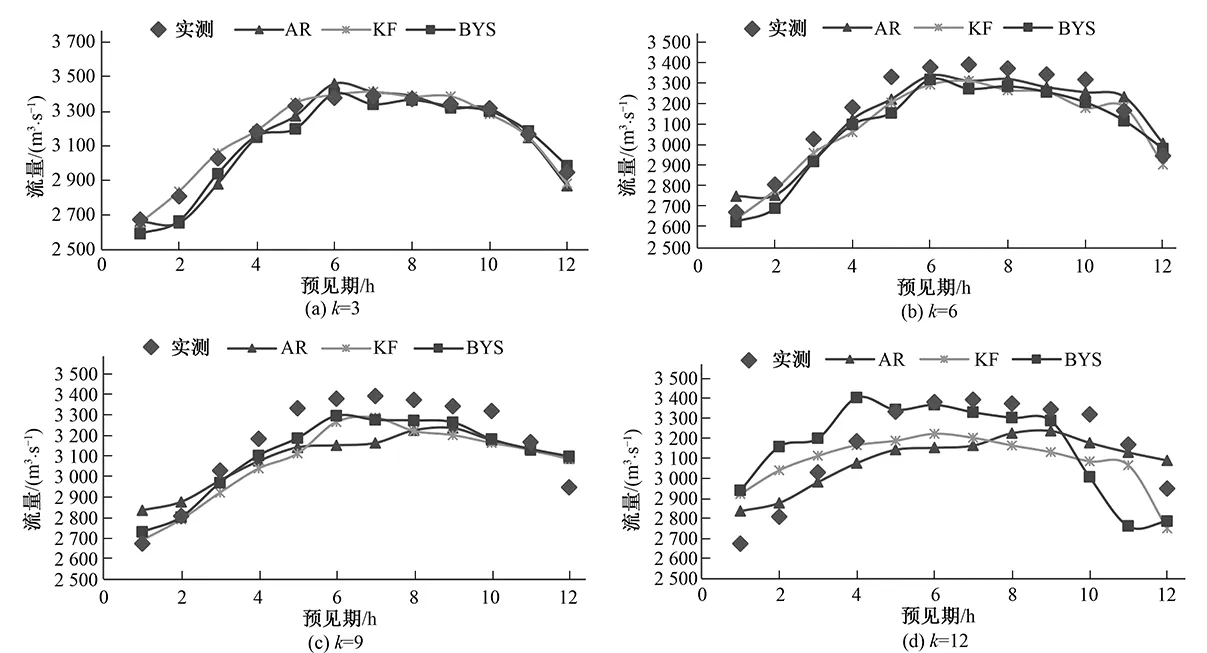
图6 不同预见期3种方法预测值与实测比较Fig.6 Comparison between predicted and measured values of three methods in different forecast periods