基于多维非稳态导热乘积法的粮粒热物性测定

陈清华苏国用孙美华姜阔胜刘 萍

(1. 安徽理工大学机械工程学院，安徽 淮南 232001；2. 智能矿山技术与装备安徽省重点实验室，安徽 淮南 232001)

中国是农业和粮食消费大国，粮食储存对保障国家安全和社会稳定意义重大，如何实现粮食的安全储藏一直是研究热点之一[1-2]。研究[3]表明冷却干燥通风可以控制粮堆温湿度，进而实现粮食的长期安全存放，而粮食作为典型的多孔介质，干燥通风过程中其内部的传热传质规律较为复杂。导热系数、热扩散率等作为粮食的重要热物性参数，由于可直接表征粮食传递热量的能力[4-5]，其准确获取对于指导和优化粮食干燥和安全储藏工艺至关重要。由于多孔介质传热机理较为复杂，试验测试仍是获取其热物性参数的主要手段[6]。例如谷和平等[7]和龚红菊等[8]分别运用正规状况法及Dickerson圆桶瞬态热流法，对颗粒状堆积物、稻谷的导热系数和热扩散率进行了试验测试。但现有测试方法中，较少的对试验过程中粮堆内部热量的侧向流动进行考虑，从而使测试精度受到一定的影响。文献[9]提出基于非稳态导热乘积法测颗粒状材料热扩散系数，优点是消除了侧向热流误差带来的影响，因而更适用于松散物料热物性测试。在此基础上，岳高伟等[10]利用高低温交变湿热试验箱设定温度边界(-50～100 ℃)，将应用范围扩展至低温环境。由于非稳态导热乘积法模型只能直接测算热扩散系数a，如需获取比热容Cp和导热系数λ，仍需借助磁力搅拌水卡计[11]等测试手段，大大限制了其推广应用性。通过易于获取的数据信息结合明确的数学模型，反演或估计被研究对象的多个参数被称为多宗量传热反问题[12]，目前已在多个领域得到应用并被认可。本试验拟基于多维非稳态导热乘积法数学模型，并结合参数估计法[13-14]对粮食颗粒的导热系数λ、比热容Cp等进行反演计算，本测试方法试验操作难度较低，便于获取高效准确的粮粒热物性参数，进而为制定粮食储藏技术方案提供科学依据。

1 数学模型

在某一刻τ将一直径为D，高为δ，上端面绝热，初始温度为t0的短圆柱体，放入温度为tw的恒温环境中。设其温度分布与角度无关，则其导热微分方程见式(1)[15]。

(1)

式中：

T——温度，℃；

r——径向变量，m；

x——轴向变量，m；

α——热扩散系数，m2/s。

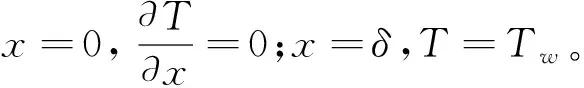
显然该问题为二维非稳态热传导问题，一般采用数值解法，但其步骤复杂且不易编程实现。介于此，试验中引用多维非稳态导热问题的乘积解法[15]。如图1所示，一短圆柱体由直径为r的无限长圆柱和一块厚度为x的无限大平板垂直相贯而成，则有：

T(R,x,τ)=[T(x,τ)]×[T(r,τ)]。

(2)

式(1)的解析解：

(3)

式(3)中包含无穷级数，显然难以直接求解，根据试算取级数前6项即可满足精度要求，式(3)可改写为：

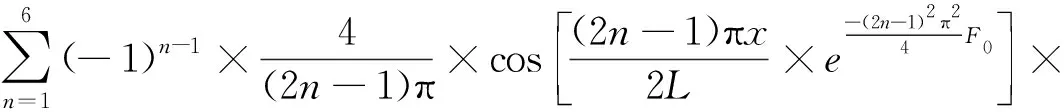
(4)

式中：

θ(r,x,τ)——短圆柱过余温度，℃；

θ(x,τ)——无限大平板过余温度，℃；

θ(r,τ)——无限长圆柱过余温度，℃；

θ0——初始过余温度，θ=t-tw，其中t为任意时刻试样温度，℃；

tw——恒温箱内部温度，℃；

L——无限大平板厚度，m；

R——无限长圆柱半径，m；

μn——特征值；

F0——傅里叶数，F0=ατ/y2，其中α为热扩散系数(m2/s)；y为特征长度；对于无限大平板y=L，对于无限长圆柱体y=R。

根据热扩散率公式a=λ/(ρCp)，显然如果已知试样密度ρ、导热系数λ、比热容Cp及厚度δ等物理参数，可计算得到短圆柱体内任意一点x处，τ时刻的无量纲过余温度θ(r,x,τ)，此为传热正问题。

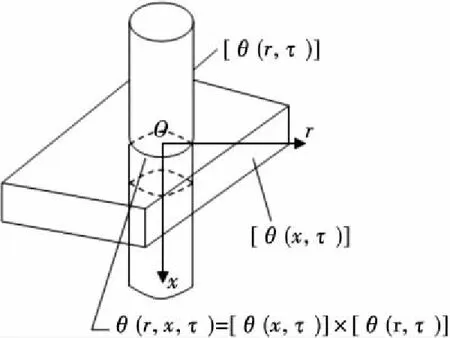
图1 非稳态导热乘积法原理图

2 热物性参数估计灵敏度分析

为研究试样内任意一点处的温度Y(τ,η)变化规律，某一时刻τ将试样放入温度为tw的环境中，温度扰动记为u(τ)。考虑试样的导热系数λ、比热容Cp等热物性参数，以及环境温度tw、时间τ、空间位置等因素都会影响u(τ)的值，故将这些参数构成一个向量：

η=(η1,η2,η3,……,ηm)T，

(5)

式中：

m——参数个数。

显然，在试验过程中对于一个确定的温度测点，式(5)中未知参数η1，η2为试样的λ和Cp。取试样中同一高度处，距中心轴均为r的k个离散测点处的温度测量值记为Yi(τ,η)(i=1,……,k)，然后给出一组λ和Cp的估计值，根据式(4)计算出的过余温度记为θ(τ,η)，各离散测点i的过余温度记为θi(τ,η)(i=1，……，k)，并进行对比：

(6)

由于测量误差以及参数估计具有随机性，Yi(τ,η)与θi(τ,η)之间必然存在偏差，即ε(η)>0。为此，参数估计的目标是基于式(4)迭代，使偏差ε(η)→min。参数向量η中的λ和Cp值要能同时以足够的精度估计出来，必须满足在最小二乘估计意义下，在参数估计的时间区间内，参数的灵敏度线性无关。本试验中灵敏度是指θ(τ,η)对参数η的一阶偏导。同时，考虑到方程式的复杂性，直接求偏导数较为困难，采用二阶中心差商进行计算：

Xij=[θ(τi,η1,……,ηj+△ηj,……,ηm)-θ(τi,η1,……,ηj-△ηj,……,ηm)]/(2△ηj)，

(7)

式中：

Xij——τi时刻θ(τi,η)对参数ηj的灵敏度系数。

通常取△ηj=0.000 1ηj。

只有在λ和Cp线性无关时，2个参数才能同时估计，因此在估计之前进行灵敏度相关性分析。分别选取玉米和稻谷进行研究。根据参考文献[16]和[17]分别选定玉米的相关参数为：密度750 kg/m3，导热系0.176 5 W/(m·℃)，比热容1 500 J/(kg·℃)，含水率17%；稻谷参数为：密度1 480 kg/m3，导热系数0.099 5 W/(m·℃)，比热容911.9 J/(kg·℃)。

由图2、3可以看出，玉米和稻谷的导热系数和比热容参数灵敏度线性均不相关，但比热容Cp灵敏度均非常小(仅为10-3数量级)，若直接进行参数估计，反演得到的比热容与实际相差较大[14]。

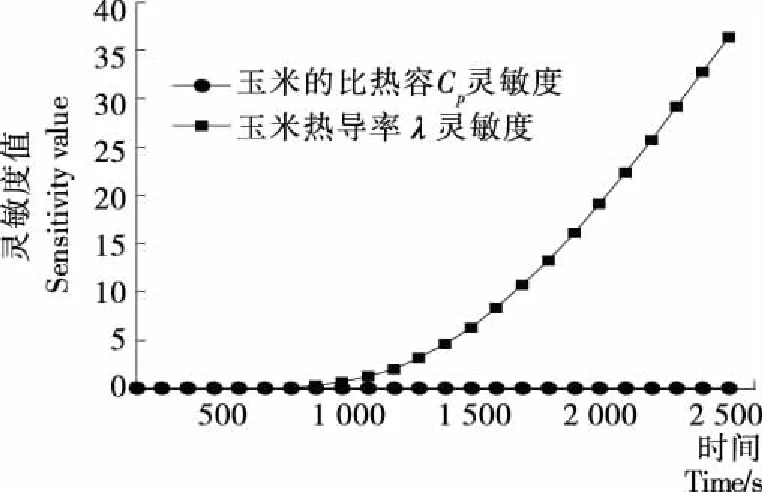
图2 玉米试样导热系数及比热容灵敏度值

图3 稻谷试样导热系数及比热容灵敏度值

3 关键技术

基于多维非稳态导热乘积法原理，设计测粮食热物性参数的测试系统，需要解决的关键技术有测试系统构建、多维非稳态传热条件、参数估计算法等。

3.1 测试系统设计

如图4所示，系统主要由恒温箱、信号采集与传输模块、信号发射端和接收端、试样筒、温度传感器和微型计算机等构成。为了避免在恒温箱上开孔影响恒温箱效果，以及增加试验操作难度，系统采用深圳蜂汇公司型号为Z-0004的ZigBee无线数据采集模块实现信号采集与传输。恒温箱温度范围为0～100 ℃，控温精度±0.1 ℃；测温热电偶精度±0.2 ℃；ZigBee数据采集模块的射频芯片CC2530的接收灵敏度为-97 dBm，有效保证了温度的实时传输。系统软件通过LabView编程建立基本松散物体参数输入区、采集温度变化显示区、控制按钮区和计算结果区等，便于对测试结果的观察以及对不同粮食颗粒测算参数设置。

1. 采集信号接收端 2. 微型计算机 3. 信号采集与传输单元 4. 绝热端盖 5. 恒温箱 6. 试样 7. 试样筒体 8. 温度测点 9. 采集信号发射端

图4 测试装置简图

Figure 4 Diagram of testing system

3.2 非稳态导热乘积物理边界的实现

根据非稳态导热乘积法原理及物理模型要求，试样为圆柱形，同时上表面绝热，下表面和圆柱面为恒温边界。此处利用恒温箱实现恒温环境，并设计圆柱形试样筒盛放试样，为保证试样放入恒温箱后较短时间内与环境温度保持一致，筒体采用黄铜制作，在内壁设置温度测点，待温度与环境温度一样时开始试验测试，以此实现圆柱面和下表面的恒温边界条件。同时，试样筒上端盖为绝热棉制作，形成试样上绝热表面。

3.3 比热容Cp灵敏度较低问题的处理

针对试验选用的材料Cp灵敏度较低，比热容不可直接估算，采用随机共轭梯度法进行求解[18]，由于式(4)中的F0=aτ/y2，只有一个未知数a，因此，首先反演估算a，然后利用a对估计的Cp值进行修正，具体流程(见图5)：

① 反演估计a；

② 估计材料λ及Cp的原始估计值；

③ 根据式(4)、(5)、(6)求得满足精度要求的a及λ；

④ 根据a估计值对原始估计值Cp进行修正，得到最终值Cp*。

为避免在测试过程中，因外界干扰因素造成的个别数据波动对估算结果造成影响，本试验首先计算出每个特定时刻τ对应的一组数值λ和Cp*，然后对计算出的一系列物性参数求加权平均作为最终参数的估计值。

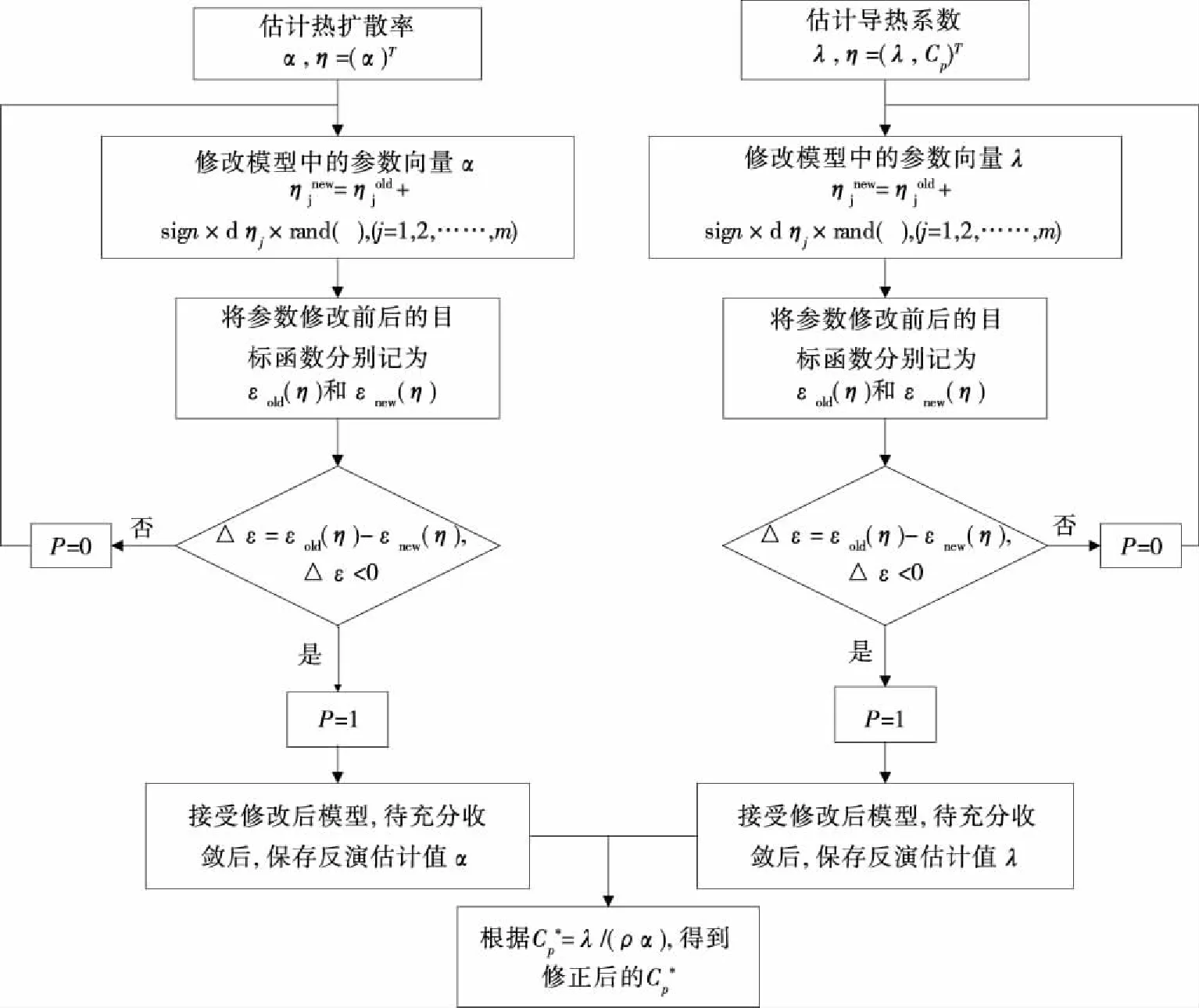
图5 参数估计流程图

3.4 温度测试准确性及可靠性

当材料质地均匀，满足各项同性的性质时，温度测点的布置对物性参数测算结果的影响不大。因此，试验前对稻谷颗粒进行筛选，装入箱体时进行压实处理。同时，在离圆柱侧面和底面相同距离的不同位置处，安装多个温度传感器，并取加权平均作为最终测试结果。此外，系统采取无线信号发射与接收的方式，有效保证了试验箱体内部为恒温边界条件，减少外界环境温度对测试结果的影响。

4 热物性测试试验分析

4.1 粮食颗粒热物性参数测试

选取淮南地区含水率为10.5%的皖稻121。首先利用孔径为2 mm的筛网对稻谷进行筛选，然后装入直径为400 mm，高为80 mm的短圆柱筒试样盒中，填充密度580 kg/m3，环境温度20 ℃，恒温箱温度保持90 ℃。在离试样筒壁面和底面均为40 mm的位置处布置2个温度测点，取平均值作为最终测试值，依次编号为测点1和测点2。某一时刻τ突然将圆柱体试样盒放入恒温箱内，同时观察铜板内壁面温度变化，当铜板内壁温度稳定且趋近于恒温箱体内部温度时，开始采集稻谷内部测点温度。为消除试验初期，测试温度的不稳定对测算结果的影响，选取100 s以后的采集数据为分析对象，试验共进行3 600 s，温度采样间隔10 s，各测点温度曲线见图6。

热扩散率α初始猜测值为2.02×10-7m2/s，导热系数λ和Cp初始猜测值分别为0.099 0 W/(m·℃)和823 J/(kg·℃)，取参数估计结果见表1。

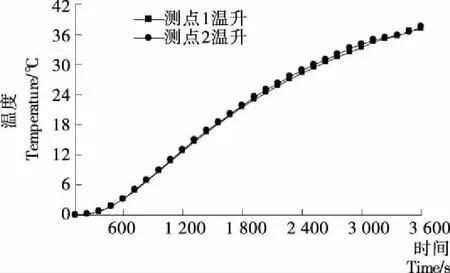
图6 测点1、测点2的温升曲线

可以看出热扩散率和导热系数估计结果与文献[17]中的测算结果较为接近，但比热容误差较大(>10%)，而修正后的比热容则较为吻合。为进一步验证测算结果准确性，对同一种试样在相同条件下进行多次试验，通过相对偏差△η衡量测算值彼此接近的程度。

(8)

式中：

由表2可以看出，导热系数与热扩散率参数反演结果以及修正后的比热容Cp*与对应平均值的最大相对偏差均小于7%，即试验满足可重复的要求。

表1 参数估计结果

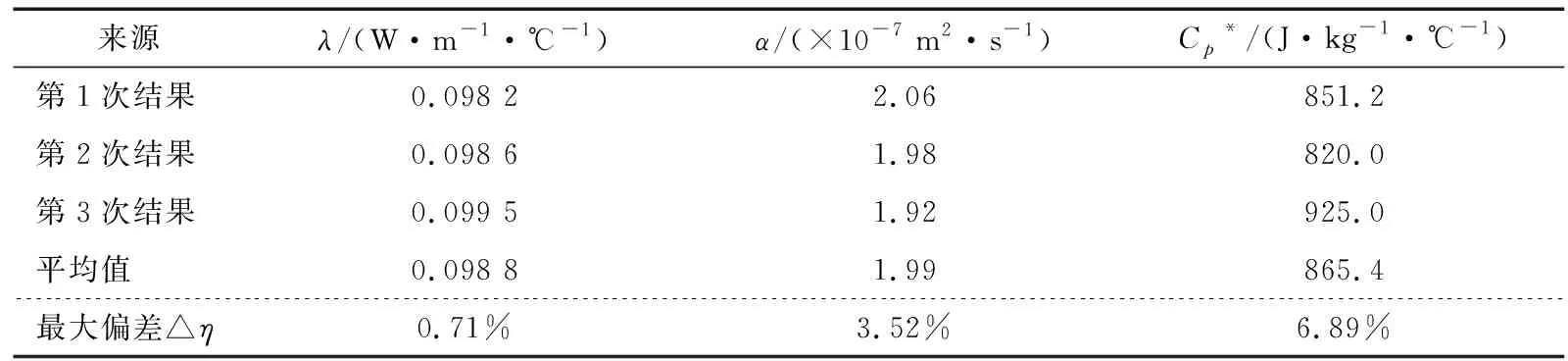
表2 参数估计试验可重复精度分析

4.2 理论计算与数值仿真结果对比

将表2中获取的热物性参数的平均值代入式(4)中，计算τ在100～3 600 s时的温度理论值，同时在Fluent中仿真模拟稻谷内部的温度场变化。数据曲线对比见图7。

由图7可以看出，稻谷的仿真曲线、理论计算曲线与实测温升曲线三者较为吻合，进一步验证了参数估计的准确性。值得注意的是，试验至约2 600 s后，实测温升与仿真和理论计算温升开始出现偏差，且随时间的延长，偏差具有变大趋势。原因可能是热量传递至试验箱上端绝热边界后因无法及时转移，造成热量积聚效应，进而对测点温度产生影响，使实测温升偏大，且随着热量积聚越来越多，影响也就越来越明显。从而为尽量消除此因素的影响，选取100～2 500 s 时的温升为最终有效测算数据。

4.3 3种粮食颗粒热物性参数测试分析

为进一步验证测试系统的稳定性与准确性，分别选取材料Y两优900水稻、联创11号和源育15玉米作为试样，含水率分别为13.1%，5.0%，12.5%，填充密度分别为600，720， 800 kg/m3。

图7 实测、理论与数值仿真温升曲线对比

由表3数据可以看出，测得的热导率λ与文献[16]和[17]数据较为接近，其中“源育15”号玉米的导热系数与文献数据相对误差最大，为4.64%，分析原因可能是不同品种的玉米本身的热物性参数存在差异，且玉米粒与稻谷相比颗粒直径较大，存入试验箱时，玉米颗粒之间的孔隙较大，测温过程温度波动较大，最终导致测算结果与参考值有偏差，但仍小于5%。符合测试精度要求。

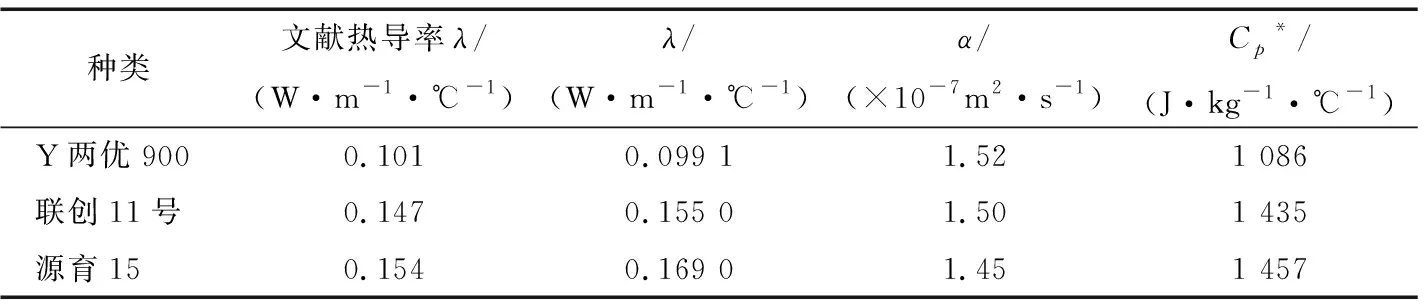
表3 3种粮食试样测试结果综合分析

5 结论

(1) 采用恒温箱结合黄铜短圆柱试样盒构建的恒温边界模型便于控制实现，且运用非稳态导热乘积法结合参数估计法对粮食颗粒的热物性参数进行测试在原理与技术上均是可行的。

(2) 采用ZigBee无线数据采集方式，数据采集更方便，且不受试验箱体结构的限制，降低了试验操作的难度。

(3) 粮粒的比热容Cp的灵敏度系数较小，需先估计再修正，才能得到较为准确的估计值。利用估算的热物性参数值通过理论计算与数值仿真温升变化曲线与实测温度变化曲

线一致，进一步说明了参数估计的准确性；对包括皖稻121在内的4种粮食进行热物性测算，结果与相关文献吻合，能够满足实际应用要求。